斜坡堤越浪量影響因素的數值研究

郭立棟，孫大鵬，黃明漢，左衛廣

（1.中交第一航務工程局有限公司，天津 300461；2.大連理工大學海岸和近海工程國家重點實驗室，遼寧 大連116024；3.中交天津港灣工程研究院有限公司，中國交建海岸工程水動力重點實驗室，天津 300222）

0 引言

斜坡堤作為一種近岸防護型結構物在近海工程中得到了普遍應用。當波浪傳播到斜坡堤時會產生顯著變形，并在斜坡上破碎，給斜坡帶來局部集中的動水壓力和底流，當波浪較大時，堤頂還會出現越浪現象。越浪通常采用越浪量作為評價、計量及控制的參數。

越浪時波浪會不斷地沖擊堤頂，使得防波堤遭受破壞，嚴重時會形成潰堤，對堤后居民的生命財產及工農業設施造成無法估量的損失。因此，越浪量是衡量斜坡堤安全性及有效性的重要指標。同時，越浪也是波浪水動力問題的一個難點，原因在于其形成過程受到多種強非線性現象的作用，例如，波浪翻卷、破碎、沖擊等。此外，對越浪量有影響的物理因素也非常多。因此，開展斜坡堤越浪研究具有非常重要的學術意義與工程價值。

最初，學者們使用模型實驗對近海工程中出現的越浪進行研究，并給出相應的越浪量公式，例如：Van der Meer和 Jenssen[1]、Hebsgaard 等[2]。通過物模實驗，可以獲得直觀、可靠的結果，但是這種方式投資大，周期長，并受到工況的限制以及模型比尺效應的影響。

目前，越浪的理論研究成果還比較少，且大部分數值計算是依托Fluent平臺，例如：王鵬等[3]、劉亞男等[4]。對于越浪的數值模擬結果，大多關注的是越浪過程中波面和越浪量變化，而對越浪量影響因素尚沒有形成系統研究。因此，本文采用0-1BEM+VOF[5]耦合模型對越浪量進行系統分析，具體研究了斜坡堤斷面形式（胸墻高度、平臺超高、平臺寬度、外堤坡度）與波浪要素（波陡、相對水深）等因素對越浪量的影響。

1 數值模型

0-1BEM+VOF模型[5]是一種新型的波浪耦合數值模型。該模型是以BEM方法與VOF方法的數值特點為基礎，前域采用0-1BEM模型模擬造波以及波浪的傳播、變形，后域模擬波浪與結構物的相互作用則采用的是雷諾時均VOF湍流模型。0-1BEM+VOF模型的計算精度、計算效率、存儲效率以及模型適用性均要優于VOF方法，同時發揮了VOF方法在自由表面追蹤上的優勢，并且特別適用于大范圍波動場的計算。

由圖1所示，模型中與越浪量有關的物理因素為：堤前水深d、波長L、波高H、堤頂到靜水位高度（胸墻高度）Hc、平臺標高Hr、平臺寬度B，外側坡度m。

入射波采用規則波，越浪量的關系式為：

式中：Q是單個波通過單寬堤頂的流量。

為便于統計分析單寬越浪量，計算單個波浪的波峰體積A：

那么，越浪量可由下式表示：

式中：μ是越浪量系數。

以物模實驗的經驗公式[6]為依據，通過式（1）和（3）的聯立，進而得到越浪量系數的無因次關系式：

探討公式（4）括號中的6個無因次變量，這里應用二變量關系式法，以Hc/H作為基本變量（考慮到胸墻高度的重要性），其它變量作為次變量，關系式為：

式中：x是式（4）的其它變量中的任一變量。

由文獻 [5]所得結論：較合理的耦合域位置是距離結構物0.8 L~1.2 L處；較合理的耦合域長度為LTD=0.1 L~0.25 L。所以，本文在越浪計算時，將耦合域取在距離斜坡堤堤腳0.8 L處，耦合域的長度取為0.2 L。將賀朝敖[6]的實驗結果作為本文計算結果的比對分析對象，并以此為基礎，探討上述各物理因素對越浪量的影響。

2 越浪量影響因素的數值分析

2.1 胸墻高度

胸墻高度是越浪量的關鍵影響因素，所以首先分析胸墻高度與越浪量之間的關系。具體方法為其它變量條件固定，計算不同Hc/H時的越浪量。其它變量條件：H/L=1/20，d/H=3.1，B/L=0.05，Hr/H=0，m=1.5。由于此時的H/L，d/H，B/L，Hr/H，m均為常數，故式（5） 中的越浪量系數僅是關于Hc/H的函數，即：

圖2是μ-Hc/H關系曲線。虛線是由實驗所擬合的經驗公式值。

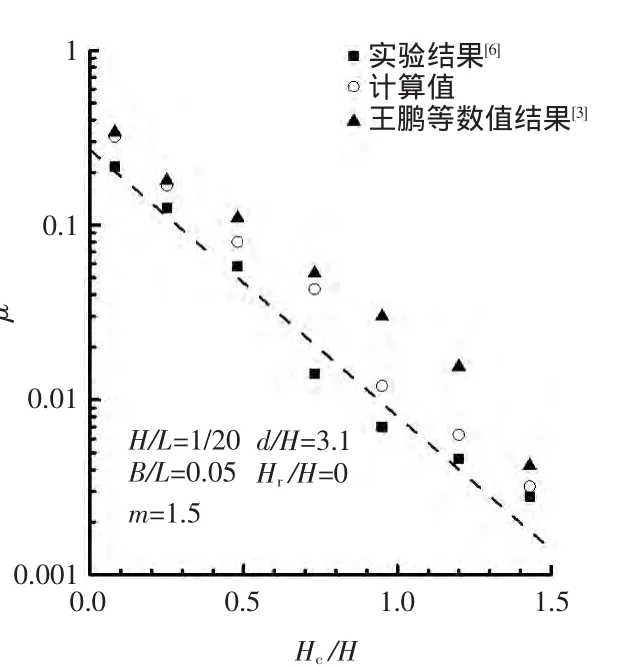
圖2 μ-H c/H關系曲線Fig.2 μ-H c/H relation curve

由圖2可知：所有點都位于對數坐標的1條直線附近，且離散性比較小；計算結果較實驗結果略大，整體吻合度比較高；相比王鵬等[3]的計算值，本文的計算值更接近實驗值，尤其在相對胸墻高度Hc/H較大時；μ和Hc/H存在指數反比關系，隨著Hc/H加大，越浪量系數逐漸減小。

2.2 平臺超高

分析平臺超高與越浪量之間的關系。具體方法為其它變量固定，計算不同Hr/H時的越浪量。3組平臺超高Hr/H=-0.5，0，0.5，負號代表在水面以下。其它變量條件：H/L=1/20，d/H=3.1，B/L=0.05，m=1.5。將實驗值（實心）、實驗擬合經驗公式（虛線）與本文計算值（空心）繪制在圖3中。由圖3可見，計算結果較實驗結果略大，整體吻合度比較高；Hr/H不同時，越浪量同Hc/H存在半對數的線性關系，其斜率k（參考圖中虛線）與Hr/H成正比，Hr/H較大時，斜率k也較大；隨著相對平臺超高Hr/H加大，越浪量系數減小。

圖3 μ-H r/H關系曲線Fig.3 μ-H r/H relation curve

2.3 平臺寬度

分析平臺寬度與越浪量之間的關系。具體方法為其它變量固定，計算不同B/L時的越浪量。4組平臺寬度為B/L=0，0.05，0.11，0.16。其它變量條件：H/L=1/20，d/H=3.1，Hr/H=0，m=1.5。將實驗值（實心）、實驗擬合的經驗公式值（虛線）與本文計算值（空心）繪制在圖4中。由圖4可見，計算結果較實驗結果略大，整體吻合度比較高；B/L不同時，越浪量同Hc/H也存在半對數的線性關系，其斜率k（參考圖中虛線）與B/L成正比，B/L較大時，斜率k也較大；隨著相對平臺寬度B/L加大，越浪量系數減小。

圖4 μ-B/L關系曲線Fig.4 μ-B/L relation curve

2.4 波陡

分析波陡與越浪量之間的關系。具體方法為其它變量固定，計算不同H/L時的越浪量。3組波陡為H/L=1/30，1/20，1/15。其它變量條件：B/L=0.05，d/H=3.1，Hr/H=0，m=1.5。將實驗值（實心）、實驗擬合的經驗公式值（虛線）與本文計算值（空心）繪制在圖5中。由圖5可見，計算結果較實驗值略大，整體吻合度比較高；H/L不同時，越浪量同Hc/H也存在半對數的線性關系，其斜率k（參考圖中虛線）與H/L成正比，H/L較大時，斜率k也較大；隨著H/L加大，越浪量系數減小。

圖5 μ-H/L關系曲線Fig.5 μ-H/L relation curve

2.5 相對水深

分析相對水深與越浪量之間的關系。具體方法為其它變量固定，計算不同d/H時的越浪量。3組相對水深為d/H=2.4，3.4，4.4。其它變量條件：H/L=1/20，B/L=0.04，Hr/H=0，m=1.5。將實驗值（實心）、實驗擬合的經驗公式值（虛線）與本文計算值（空心）繪制在圖6中。由圖6可見，計算結果較實驗值略大，整體吻合度比較高；d/H不同時，越浪量同d/H也存在半對數的線性關系，其斜率k（參考圖中虛線）與d/H成正比，d/H較大時，斜率k也較大；隨著d/H加大，越浪量系數減小。

圖6 μ-d/H關系曲線Fig.6 μ-d/H relation curve

2.6 外堤坡度

分析外堤坡度m與越浪量系數之間的關系。具體方法為其它變量固定，計算不同m時的越浪量。其它變量條件：d/H=3.2，B/L=0.01，Hr/H=0，Hc/H=1，2 組波陡 H/L=1/20，1/30。故式（5） 中的越浪量系數僅是關于坡度m的函數。圖7是上述工況下的越浪量實驗值與計算結果，可知μ與m具有線性關系。

圖7 μ-m關系曲線Fig.7 μ-m relation curve

3 越浪量系數的控制分析

統計分析越浪量系數的實驗結果與計算結果，并將相同工況下的計算值與實驗值的比值（計算值/實驗值）繪制在圖8中，圖中兩條線分別為y=1.3x和y=x。由圖可見，大多數點均包含在兩條線內，這表明了計算結果較實驗值偏大，且偏差是可控的（30%）。本文分析計算結果偏大的原因為：1）差分格式的VOF。網格劃分時，差分格式VOF方法在斜坡上進行了簡化處理，它不具備強大的地形適應能力；2）越浪機理的復雜性。實際上VOF方法對破碎、水汽摻混等強非線性現象的模擬也僅是簡化的處理，而相當部分的波浪在上述作用中損耗，目前該損耗值在數值計算中仍無法準確衡量，所以爬高距離、越浪量大小等數值結果均會被高估，Hsiao與Lin[7]也有類似看法；3）物理實驗比尺效應。

圖8 實驗與計算值的對比Fig.8 Comparison of fitted valuebetween measuresand calculated values

4 結語

本文采用一種新型的波浪耦合數值模型（0-1BEM+VOF模型）對斜坡堤越浪進行模擬。為了深入研究越浪量的影響因素，數據處理時應用二變量關系式的方法，選取Hc/H作為基本變量（考慮到胸墻高度的重要性），其它變量作為次變量。通過與他人實驗結果的對比分析得出結論：相對胸墻高度Hc/H對越浪量系數具有十分顯著的影響，它們之間存在指數反比關系；其它變量對越浪量也有一定影響，隨著Hc/H的變化，變量與越浪量之間也具有指數線性關系。本文計算結果較實驗值偏大但可控。

[1]VANDERMEERJW，JANSSENJPFM.Waverun-up and wave overtopping at dikes and revetments[R].Netherlands：Delft Hydraulics，1994.

[2]HEBSGAARD M，SLOTH P，JUHL J.Wave overtopping of rubble mound breakwaters[C]//Proceedingsof theinternational conference on coastal engineering.2011，1（26）：2 235-2 248.

[3] 王鵬，孫大鵬.基于FLUENT的海堤越浪數值模擬[J].中國水運：下半月，2011（7）：73-75.WANG Peng，SUN Da-peng.Numerical simulation of wave overtopping over seawalls based on FLUENT[J].China Water Transport：thesecond half of themonth，2011（7）：73-75.

[4] 劉亞男，郭曉宇，王本龍，等.基于RANS方程的海堤越浪數值模擬[J].水動力學研究與進展：A 輯，2007，22（6）：682-688.LIU Ya-nan，GUOXiao-yu，WANGBen-long，et al.Numerical simulation of wave overtopping over seawalls using the RANS equations[J].Journal of Hydrodynamics：series A，2007，22（6）：682-688.

[5] GUO Li-dong，SUN Da-peng，WU Hao.A new numerical wave flume combiningthe 0-1 type BEM and the VOF method[J].Journal of Hydrodynamics，2012，24（4）：506-517.

[6] 賀朝敖，任佐皋.帶胸墻斜坡堤越波量的試驗研究[J].海洋工程，1995，13（2）：62-70.HE Chao-ao，RENZuo-gao.Experimental study on wave overtopping of rubble mound breakwater with vertical wall[J].The Ocean Engineering，1995，13（2）：62-70.

[7] HSIAO SC，LIN T C.Tsunami-like solitary waves impinging and overtopping an impermeable seawall：experiment and RANSmodeling[J].Coastal Engineering，2010，57（1）：1-18.