振動流化床結構動態分析

武繼達，劉初升，趙躍民，李 珺

WU Ji-da1,3，LIU Chu-sheng1,3，ZHAO Yue-min2，LI Jun1,3

（1.中國礦業大學 機電工程學院，徐州 221116；2.中國礦業大學 化工學院，徐州 221116；3.中國礦業大學 盱眙礦山裝備與材料研發中心，徐州 221116）

0 引言

振動流化床是一種新型的煤炭干法分選設備。其通過對普通流化床施加一定頻率的振動，使煤炭顆粒作拋擲運動，從而促進物料的松散分層，增加物料與干燥氣體的接觸機會，提高了傳熱系數，有利于防止煤團黏結，提高流化效果[1～3]。

但由于振動的引入，振動流化床在工作過程中，要受到物料的沖擊力、振動電機的高頻激振力、彈簧回復力和阻尼力作用，這些周期性交變載荷使得床體的受力情況惡化，容易導致結構疲勞性損壞，縮短振動流化床使用壽命[4]。本文主要研究振動流化床在工作過程中的動態特性，分析其關鍵部位應力、應變分布情況及變化規律，從而避免結構共振，減小結構的應力集中，降低整體應力，提高振動流化床的可靠性。

1 振動流化床的結構及工作原理

如圖1所示，振動流化床采用箱體式結構，主要由上箱體、下箱體、排料裝置、激振電機和支撐裝置組成。設計參數如表1所示。其中上下箱體采用鍋爐鋼直接焊成，并在內部布置有加強橫板，上下箱體采用螺栓連接，成為一個整體式密閉箱體。四個支撐裝置位置滿足k1l1=k2l2[5]，其中k1、k2為彈簧剛度，l1、l2為支撐裝置距質心的水平距離，即彈簧剛度距質心力矩為零。

振動流化床采用兩臺自同步激振電機驅動，兩臺電機的轉速、初始相位相同，旋轉方向相反，從而產生垂直于電機底座的正弦激振力，方向與水平夾角為75°。

2 振動流化床的運動學仿真

利用Pro/E5.0建立振動流化床三維模型，并導入Adams中，為減小Adams仿真時計算量，建模時將焊接固連在一起的部件做成一個零件，同時將一些對仿真結果影響不大的零件(如銷釘等)加以簡化，以減小Adams的仿真工作量，提高仿真效率。

在Adams中對振動流化床施加彈簧—阻尼支撐以及平面運動約束，并根據設計參數設置彈簧剛度、阻尼系數及重力方向，如圖2所示。彈簧總剛度，式中z為隔振系數，取z=4，f為激振頻率[6]。每個支撐裝置的彈簧剛度，彈簧阻尼C取剛度值的1%。在支撐裝置的水平方向施加彈簧，剛度取豎直方向剛度值的1/3，以模擬實體彈簧的橫向剛度[7]。

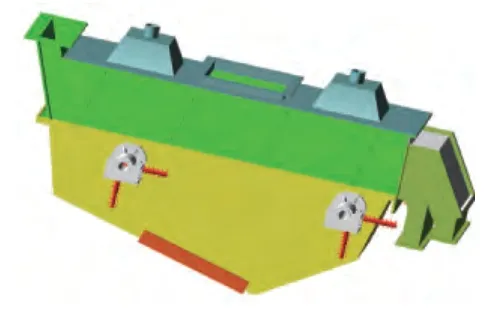
圖2 振動流化床adams仿真模型

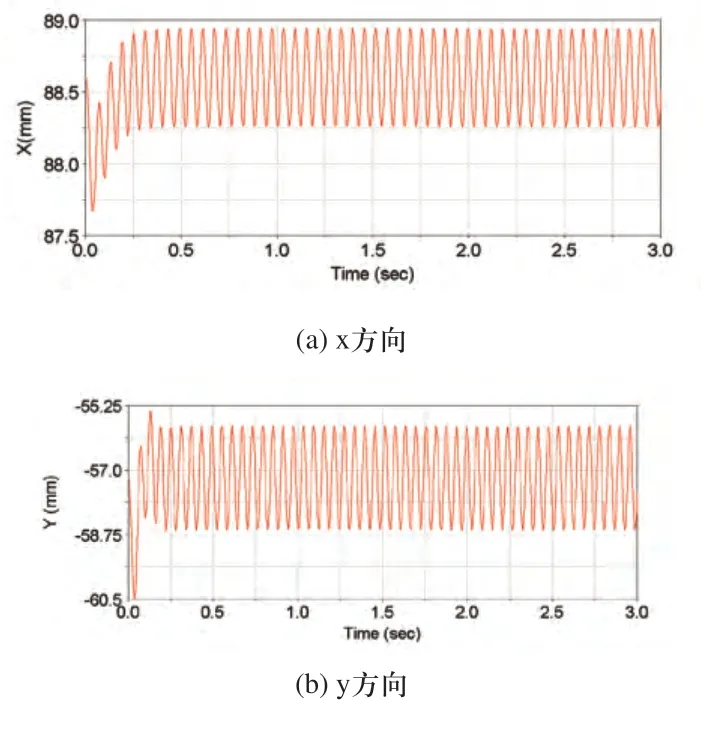
圖3 振動流化床的位移－時間關系曲線

圖4 振動流化床空間軌跡圖

從圖3、圖4可以看出，在電機啟動0～0.25s內，振動流化床運動較為劇烈，空間軌跡圖比較紊亂，這是由于激振力瞬間施加在床體上，隔振彈簧產生大的變形造成的。在0.25s后振動流化床運動趨于平穩。正常工作狀態下振動流化床位移為一平穩的正弦曲線，y方向振幅在1.41mm，x方向振幅在0.34mm，振動方向角為76.22°。運動學參數與設計要求有較好的吻合。

3 振動流化床的動力學仿真

為分析振動流化床的動態運行時的動力學特性，將Pro/E模型適當簡化后轉存為x_t格式，導入workbench中，進行模態分析，并在此基礎上利用Adams仿真所得載荷譜進行瞬態分析。

由經典理論可知，物體的通用動力學方程為[7]：

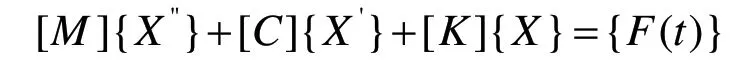
式中[M]、[C]、[K]分別是是質量矩陣、阻尼矩陣、剛度矩陣，{x''}、{x'}、{x}為對應的加速度矢量、速度矢量和位移矢量，F(t)為隨時間變化的力矢量，是系統總體載荷列陣。

模態分析主要用來求解結構的固有頻率和模態振型，從而使結構設計避免共振，并預測在不同載荷作用下的結構振動形式。結構的頻率和振型可由動力學方程的特征方程(K-ω2M)φ=0得出，其中ω為固有頻率，φ為對應的特征向量。

瞬態分析可以求解結構在隨時間任意變化的載荷作用下的動力響應，從而對結構動態特性進行評估。由于動力學問題需要考慮結構的慣性，因此需要定義模型的材料屬性。根據振動流化床所用材料，定義材料參數如下：E=210GPa，υ=0.3，ρ=7850kg/m3。

由于振動流化床主要存在的強度問題是箱體開裂，因此分析時忽略了布風板、連接螺栓等小質量物件以及其他對床體結構應力分布無影響或影響不大的部件；上下箱體及支撐裝置與側板之間定義Bond連接，采用接觸單元TARGE170和CONTA174傳遞載荷，以模擬焊接及螺栓連接；由于不考慮振動電機本身的應力應變問題，將振動電機使用同質量的點質量單元代替，并布置在電機底板相應位置。支座的三個方向上施加彈簧—大地連接，并將激振力等效為施加在電機安裝面上的當量均布力。網格劃分前對模型進行預處理，采用自由劃分法，并限制網格尺寸，以獲得較好的網格劃分質量。劃分后的效果圖如圖5所示，網格劃分時全部劃分為 Solid187，Solid186 實體單元，共形成35923個單元,139831個節點。

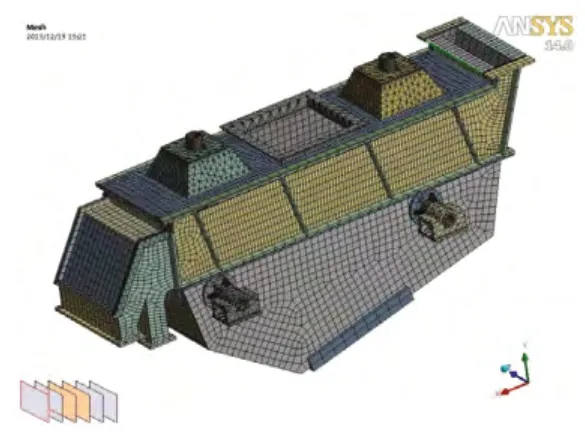
圖5 振動流化床網格劃分圖

瞬態動力學算法有三種：直接法(Full)、縮減法(Reduced)和模態疊加法(Mode Superpos’n)。本文中采用模態疊加法求解。模態疊加法是通過對模態分析得到的振型（特征值）乘上因子并求和來計算結構響應的，為此，首先對振動流化床進行模態分析，而后在workbench的Transient分析中插入pressure，對電機底板施加激振力，點擊solve進行求解。計算完成后，后處理中采用Von Mises（最大等效應力）準則對下箱體側板進行評估，得到動態應力分布云圖，如圖6所示。Von Mises公式為：

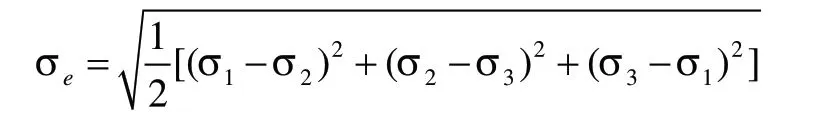
其中 σ1、σ2、σ3分別表示三個主應力，結構最大應力應小于材料的許用應力。

圖6 振動流化床側板動態應力分布圖

根據模態分析，振動流化床前十階固有頻率如表2所示。

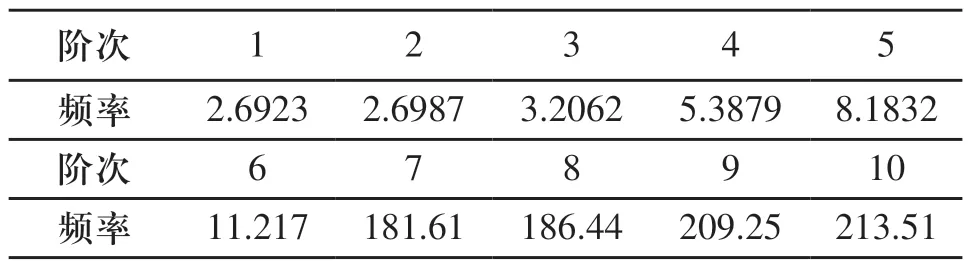
表2 振動流化床前十階固有頻率（Hz）

表2中的前六階固有頻率對應的的振型為剛體運動，由于振動流化床結構對稱，所以有些固有頻率數值非常相近。分析可得，振動流化床各階頻率均不與激振頻率16.67Hz重合，正常工作時不會發生共振。同時由圖6可以看出，最大等效應力出現在支撐裝置處，最大值為21MPa，低于振動篩行業的許用應力值24.5MPa。雖然振動流化床結構滿足強度要求，但由于強度儲備裕量較小，在長時間周期載荷作用下仍可能發生結構破壞。為此，對振動流化床結構加以改進，即在下箱體彈簧支撐裝置處增加空心圓管梁，如圖7所示，利用空心圓管梁與側板共同分擔載荷，以加強結構剛度，減小側板變形。

由于支撐裝置關于振動流化床質心對稱，因而增加圓管梁后未改變振動流化床水平質心，而豎直方向質心僅上升0.68mm，不會對運動平穩性造成影響。雖然增加了參振質量，但由于激振電機選型時有一定的裕量，因而不會對運動參數造成太大影響。

改進后，重新進行動態分析，結果如表3所示。

加強后振動流化床的前六階剛體運動的固有頻率略有降低，由特征方程(K-ω2M)φ=0可以看出，剛體運動頻率的降低主要是是由于參振質量增加造成的。由于改進后的固有頻率遠離工作頻率,頻率裕度增加，因此有利于改善振動流化床動態性能。7～10階固有頻率較改進前有明顯提高，說明圓管梁增大了結構的剛度，有利于承受外界載荷。由應力分布圖圖8可知，改進后的下箱體支撐裝置處應力值明顯降低，最大值為15.19MPa，較改進前下降了27.6%，從而驗證了結構改進的合理性。

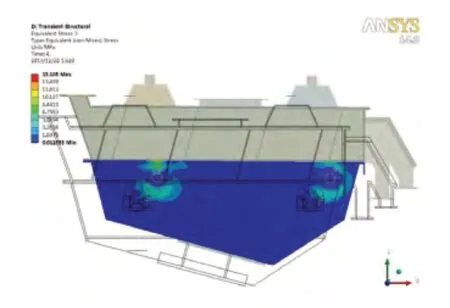
圖8 加強后的振動流化床側板應力分布圖

4 結束語

1）分析表明，該型振動流化床固有頻率遠離工作頻率，正常工作時不會發生共振造成結構損壞。

2）由于箱體式振動流化床主要存在側板開裂問題，所以對下箱體側板重點進行分析改進。通過增加空心圓管橫梁，有效改善了振動流化床工作時的動態應力分布，降低了箱體最大應力值，有利于提高其使用壽命。

[1]朱建鳳,駱振福,李振.基于物料分離的振動流化床研究現狀與展望[J].煤炭工程,2007,(9):91-93.

[2]陳清如,楊玉芬.21世紀高效干法選煤技術的發展[J].中國礦業大學學報,2001,(11):527-529.

[3]李珺,劉初升,趙躍民,彭立平.新型振動流化床的動態特性及試驗研究[J].煤炭學報,2013,(10):1882-1887.

[4]王建華,孔祥偉.振動流化床篩箱結構優化設計[J].機械工程師,2012,(7):108-110.

[5]張恩廣.篩分破碎及脫水設備[M].北京:煤炭工業出版社,1991.

[6]王峰,王皓.篩分機械[M].北京:機械工業出版社,1998.

[7]賀孝梅,劉初升,張成勇.超靜定網梁激振結構大型振動篩動態特性.煤炭學報.2008,(9):1040-1044.

[8]李范春.ANSYS Workbench設計建模與虛擬仿真[M].北京:電子工業出版社,2011.