礱谷機喂料器隔振系統的優化分析

賈樂樂 王鳳成 阮競蘭

(河南工業大學機電工程學院，鄭州河南 450007)

礱谷機振動喂料性能評價因素主要包括喂料器的喂料特性和隔振效果。其中，隔振效果的好壞通常通過隔振系數的大小加以評定，對于二次隔振系統，常采用動載荷幅值比來評判，其主要影響因子有頻率比和質量比。本研究擬對礱谷機振動喂料器在隔振方面進行參數匹配和優化，利用群體智能優化方法——粒子群算法，對該振動系統中的動載荷幅值比進行優化，為礱谷機喂料器隔振系統的設計提供參考。

1 礱谷機喂料器動載荷幅值比

1.1 動載荷幅值比數學模型

礱谷機喂料器結構簡圖如圖1所示，主要由料槽、激振器、主振彈簧、底座和隔振彈簧組成，具有輸送效率高、負載能力強和結構簡單等特點。其振動系統模型可看作是二自由度系統的受迫振動，不計阻尼的情況下，該模型可簡化為如圖2所示的結構簡圖。

根據圖2簡化模型以及拉格朗日方程，寫出振動系統的微分方程為:

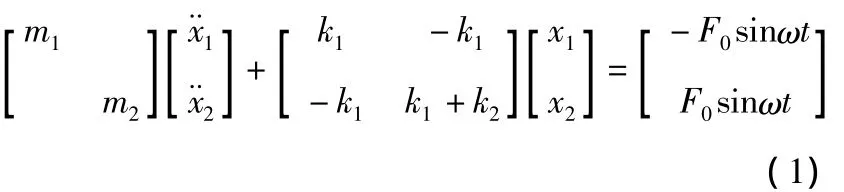
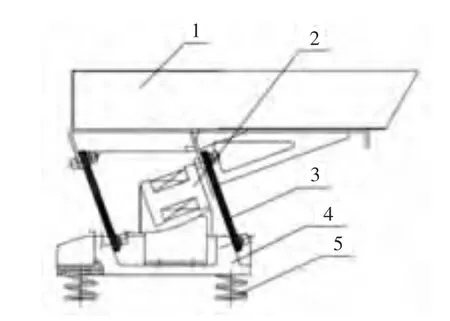
圖1 礱谷機喂料器結構簡圖Figure 1 The structure diagram of Rubber Roller Husker Feeder

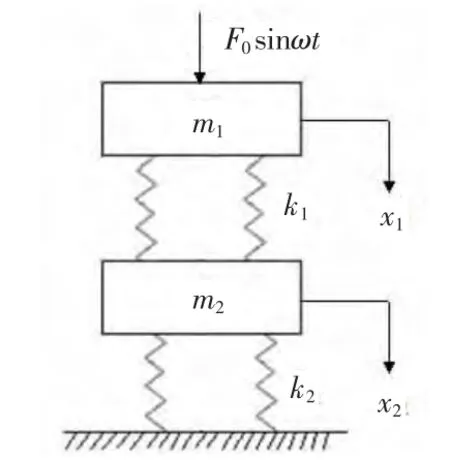
圖2 二自由度系統的受迫振動模型Figure 2 The forced vibration model of two degree of freedom system

代入求解得:

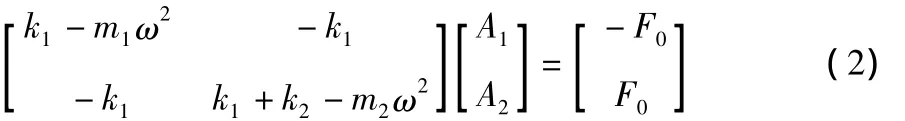
系統的固有頻率與外界的激振力及其形式無關，假設喂料器所受的激振力為0，得:

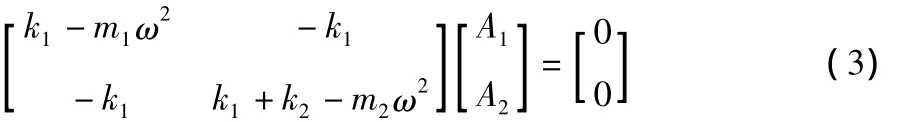
要使得方程有非零解，則:

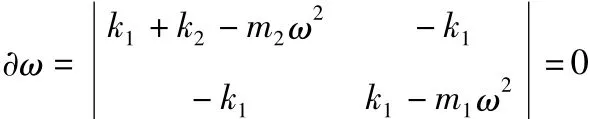
求解二自由度振動系統的兩個固有頻率ω01和ω02，簡化后為:

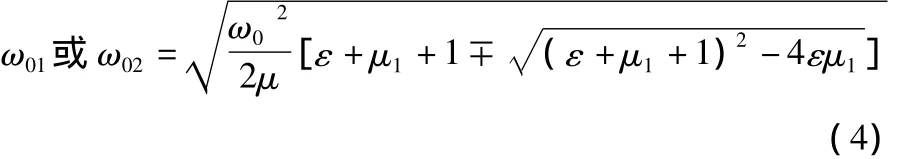
求得上質體振幅A1和下質體振幅A2的值分別為:

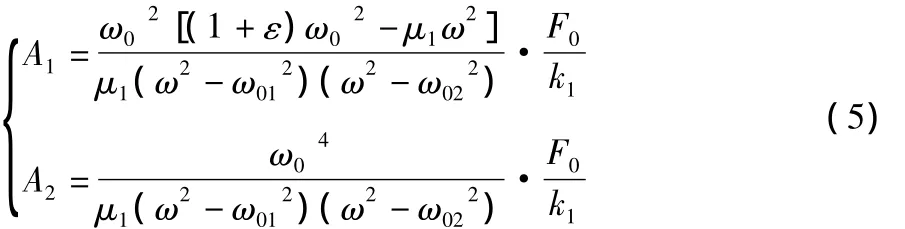
二次隔振傳給地基的動載荷為:

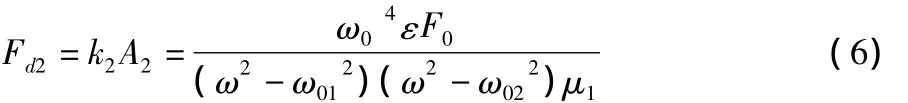
一次隔振傳給地基的動載荷為:

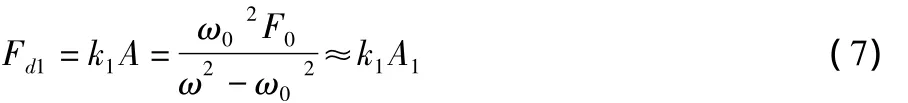
二次隔振與一次隔振傳給地基的動載荷幅值之比為:

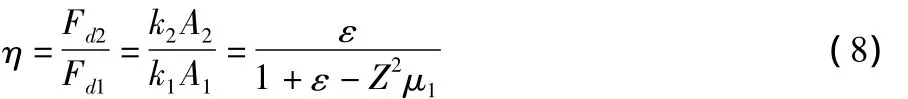
1.2 動載荷幅值比參數的數值模擬

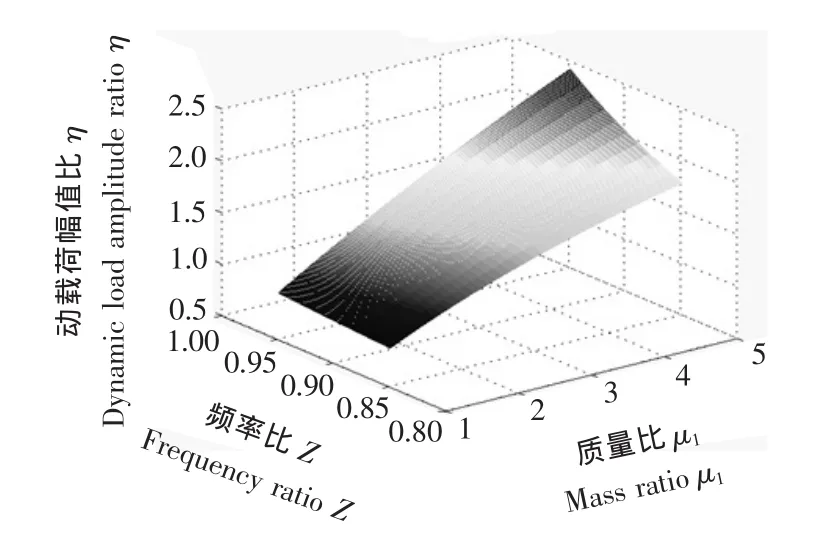
圖3 η－μ1－Z三維網格圖Figure 3 The 3D grid diagram of η － μ1－ Z

2 粒子群算法

2.1 粒子群算法優化思想

粒子群算法(particle swarm optimization，PSO)能解決連續函數的最小值問題，是一種新興的基于群體智能的啟發式全局搜索算法，是群體智能優化方法之一。與其它優化算法相比，粒子群優化算法具有規則簡單，容易實現;收斂速度快，可以避免陷入局部最優;可調參數比較少，搜索高效等優點［3］，因此，在工程中應用比較廣泛。

假設在一個D維的目標搜索空間中，有N個粒子組成一個群落，其中第i個粒子表示為一個D維的向量，記為:Xi=(xi1，xi2，…xiD)，i=1，2，…N。

第i個粒子速度是一個D維的向量，記為:Vi=(vi1，vi2，…，vid，…，viD)，i=1，2，…N。

第i個粒子搜索到的最優位置稱為個體極值，記為:Pi=(pi1，pi2，…，pid，…，piD)，i=1，2，…N。

整個粒子群搜索到的最優位置為全局極值，記為:

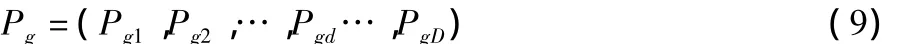
每次迭代的過程中，粒子根據式(10)和(11)來更新自己的速度和位置［4］:

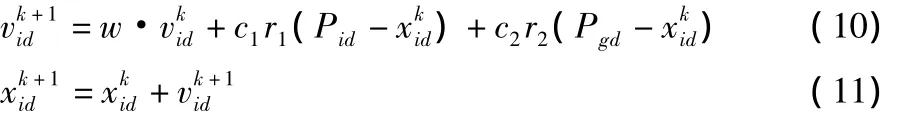
式中:

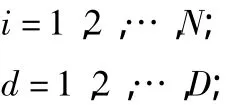
c1、c2——學習因子，也稱加速常數;

k——迭代次數;

r1、r2——［0，1］范圍內的均勻隨機數。

2.2 粒子群算法的參數變量

合適的參數變量能有效提高粒子群算法的優化速度、精度和性能，設置的主要參數包括:種群規模N、最大迭代次數M、慣性權值w、加速因子c1，c2和粒子維數D等。

(1)種群規模N:種群太小不能提供足夠的采樣點，導致算法性能很差;種群太大盡管可以增加優化信息，但會增加計算量，造成收斂時間太長，表現為收斂速度緩慢。種群規模一般設為100～1 000。

(2)最大迭代次數M:迭代次數能保證解的收斂性，但是影響運算速度。

(3)慣性權值w:慣性權重w表示在多大程度上保留原來的速度。w較大，全局收斂能力強，局部收斂能力弱;w較小，局部收斂能力強，全局收斂能力弱，合適的慣性權重值可以平衡該算法的全局和局部尋優能力。通常情況下，w=0.1～0.9。

(4)加速因子c1、c2:加速常數c1和c2用于控制粒子指向自身或鄰域最佳位置的運動。c1和c2值選擇過大，粒子將會很快地越過目標區域;若選擇過小，粒子將會飛離目標區域。合適的加速常數可以提高算法的速度且不陷入局部最優，通常取c1=c2=2。

(5)粒子維數D:粒子維數取決于待優化函數的維數。

3 優化過程及結果分析

根據粒子群優化算法的思想［5］，針對原MLGQ36型膠輥礱谷機喂料器，以其動載荷幅值比為目標函數，編制相應的粒子群優化程序，主要包括主程序、更新粒子速度及位置的程序和求解程序3部分［6］，其中的參數值設置見表 1［7］，所得優化后的結果見圖4［8］。

表1 粒子群優化算法中參數設置Table 1 Parameter Settings on PSO

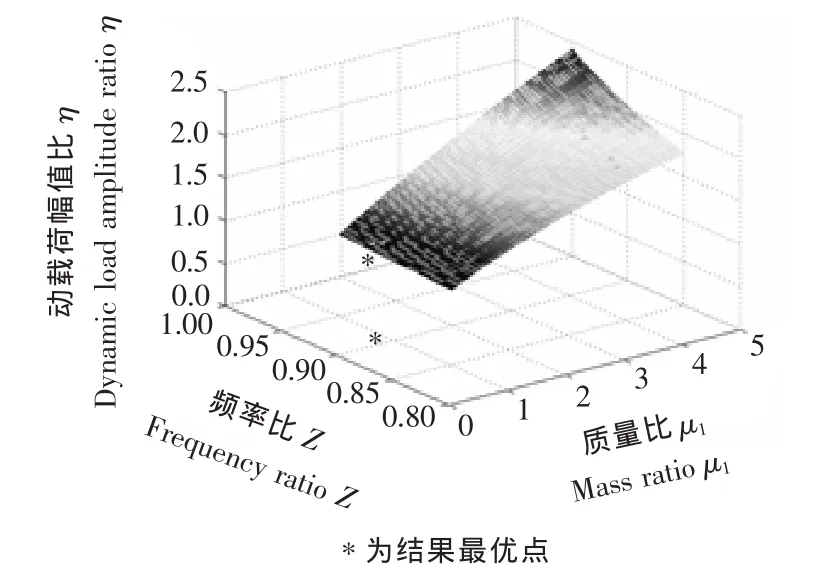
圖4 粒子群優化結果Figure 4 The results after Particle Swarm Optimization

由粒子群優化結果可以看出，當頻率比Z≈0.9，質量比μ1≈0.8時，動載荷幅值比取極小值 η≈0.836 4。優化前后結果對比如表2所示，優化后的動載荷幅值比要比優化之前小，說明優化后傳給機架的動載荷較小，方案可行。

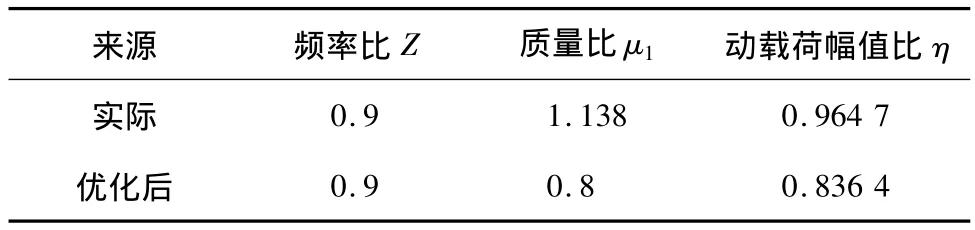
表2 優化前后結果對比Table 2 The pre and post optimization results compared

對于近共振振動機械，其主振頻率比Z=ω/ω0≈1，通常選用的范圍為Z=0.75～1.30。此時，若采用一次隔振時，隔振系數 η=k/mω2= ( ω/ω0)2=1/Z2;采用二次隔振可以有效降低傳入機架的動載荷，減小整機的振動和噪音，對于振動喂料器來說，隔振系數必須小于許用值，需保證［η］＜1.11～1.38［9］。優化后所得的結果小于許應值，滿足實際工況所需的隔振效果。

4 結論

通過對礱谷機喂料器隔振系統進行建模和分析，得出二次隔振系統的動載荷幅值比關系式。針對原MLGQ36型礱谷機喂料器，利用MATLAB軟件編制出相關的粒子群優化程序，以動載荷幅值比為目標函數，對其進行智能優化。結果表明，當振動系統中的頻率比選擇在Z=0.9附近，質量比選擇在μ1=0.8附近時，動載荷幅值比取極小值η≈0.836 4。所得的結果較為優化，且滿足實際工況的隔振效果，使得該喂料器傳入機架的振動低、噪聲小。

1 聞邦椿，劉樹英.振動機械的理論與動態設計方法［M］.北京:機械工業出版社，2001:93～94.

2 王正林，劉明.精通MATLAB［M］.北京:電子工業出版社，2013:296～298.

3 紀霞.粒子群算法及應用［M］.北京:科學出版社，2009:25～28.

4 高朝祥，王充.基于粒子群算法的曲柄滑塊機構優化設計［J］.食品與機械，2011，27(4):101 ～103.

5 雷秀娟.粒子群優化算法在函數優化中的應用及參數分析［J］.計算機工程與應用，2008，44(28):53 ～55.

6 吳建生，秦發金.基于MATLAB的粒子群優化算法程序設計［J］.柳州師專學報，2005，20(4):97 ～100.

7 Deyun.Hybrid particle swarm optimization and its application［J］.Journal of Chemical Industry and Engineering，2008，59(7):1 707 ～1 710.

8 侯志榮，呂振肅.基于MATLAB的粒子群優化算法及其應用［J］.計算機仿真，2003，20(10):68 ～70.

9 祝水琴.基于MATLAB軟件的電磁振動喂料系統仿真［J］.輕工機械，2009，27(2):65 ～67.