BP與小波神經(jīng)網(wǎng)絡(luò)短時(shí)交通流預(yù)測(cè)對(duì)比研究

王 健 孫結(jié)松

（江蘇緯信工程咨詢有限公司，江蘇 南京 210014）

0 引言

隨著經(jīng)濟(jì)、社會(huì)的發(fā)展，越來越多的人選擇使用小汽車出行，導(dǎo)致城市交通壓力迅速增大，許多大城市如北京、上海的交通不堪重負(fù)，好在近年來很多國內(nèi)的學(xué)者開始急切關(guān)注交通問題，提出很多解決的方案。智能交通系統(tǒng)（intelligent transportation system，ITS）作為一種實(shí)時(shí)、高效、準(zhǔn)確、便民的交通系統(tǒng)開始作為解決交通問題的新手段進(jìn)入人們的視野，很多專家預(yù)言未來要想緩解城市交通壓力，ITS 具有非常重要的作用。

交通流預(yù)測(cè)是城市交通控制和誘導(dǎo)的基礎(chǔ)。只有在全面提前掌握城市各路段交通動(dòng)向，決策人員才能據(jù)此做出準(zhǔn)確的判斷，合理調(diào)配交通流。交通流預(yù)測(cè)是指根據(jù)現(xiàn)有的交通流數(shù)據(jù)，預(yù)測(cè)下一時(shí)刻（最多為5min）的交通流量、交通速度、交通密度。本文重點(diǎn)研究如何預(yù)測(cè)下一時(shí)刻（取15min）交通流量。

短時(shí)交通流預(yù)測(cè)研究受到廣泛關(guān)注，現(xiàn)已發(fā)展了很多成熟的理論方法。典型的預(yù)測(cè)方法是以統(tǒng)計(jì)分析方法為基礎(chǔ)，但由于短時(shí)交通流往往具有迅速而劇烈波動(dòng)且體現(xiàn)頻繁的交通擁堵的特征[1]，所以短時(shí)交通流數(shù)據(jù)常常是非線性的，通過數(shù)據(jù)分析，其非線性特征在早晚高峰期尤為明顯。所以這些以線性預(yù)測(cè)為基礎(chǔ)的方法往往預(yù)測(cè)精度不高，結(jié)果不理想。為適應(yīng)短時(shí)交通流變化的非線性性，出現(xiàn)了一些改進(jìn)的模型，比較成功的是卡爾曼濾波等方法。

隨著數(shù)學(xué)研究的進(jìn)展，許多非線性理論方法被應(yīng)用于短時(shí)交通流預(yù)測(cè)，針對(duì)短時(shí)交通流變化的隨機(jī)性和非線性性，出現(xiàn)了以神經(jīng)網(wǎng)絡(luò)、模糊理論、混沌理論和元胞自動(dòng)機(jī)等非線性系統(tǒng)理論為基礎(chǔ)的非線性預(yù)測(cè)模型[2]，也有一些學(xué)者通過仿真和神經(jīng)網(wǎng)絡(luò)相結(jié)合的方法對(duì)此進(jìn)行深入研究[3]。由于小波神經(jīng)網(wǎng)絡(luò)可避免BP 神經(jīng)網(wǎng)絡(luò)等結(jié)構(gòu)設(shè)計(jì)上的盲目性，并且網(wǎng)絡(luò)權(quán)系數(shù)線性分布和學(xué)習(xí)目標(biāo)函數(shù)的凸性，使網(wǎng)絡(luò)訓(xùn)練過程從根本上避免了局部最優(yōu)等非線性優(yōu)化問題，同時(shí)兼有較強(qiáng)的函數(shù)學(xué)習(xí)和推廣能力[4]，固本文重點(diǎn)研究基于小波神經(jīng)網(wǎng)絡(luò)的短時(shí)交通流預(yù)測(cè)，并對(duì)比BP 神經(jīng)網(wǎng)絡(luò)，以比較兩者的差異。

1 小波神經(jīng)網(wǎng)絡(luò)

1.1 小波理論

小波分析是針對(duì)傅里葉變換的不足發(fā)展而來，小波變換經(jīng)常和傅里葉變換做比較，在那里信號(hào)用正弦函數(shù)的和來表示。主要的區(qū)別是小波在時(shí)域和頻域都是局部的，而標(biāo)準(zhǔn)的傅里葉變換只在頻域上是局部的。短時(shí)距傅里葉變換(Short-time Fourier transform)(STFT)也是時(shí)域和頻域都局部化的，但有些頻率和時(shí)間的分辨率問題，而小波通常通過多分辨率分析給出信號(hào)更好的表示。小波變換計(jì)算復(fù)雜度上也更小，只需要O(N)時(shí)間，而不是快速傅里葉變換的O(N log N)，N 代表數(shù)據(jù)大小[5]。

1.2 小波神經(jīng)網(wǎng)絡(luò)

1.2.1 小波函數(shù)構(gòu)建

小波神經(jīng)網(wǎng)絡(luò)是一種以BP 神經(jīng)網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)為基礎(chǔ)，把小波基函數(shù)作為隱含層節(jié)點(diǎn)的傳遞函數(shù)，信號(hào)前向傳播同時(shí)誤差反向傳播的神經(jīng)網(wǎng)絡(luò)。設(shè)x（k）為小波神經(jīng)網(wǎng)絡(luò)的輸入?yún)?shù)向量，Y（m）是小波神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)輸出向量，ωij 和ωjk 為小波神經(jīng)網(wǎng)絡(luò)權(quán)值。

則隱含層輸入計(jì)算公式為：

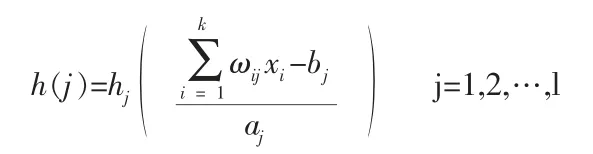
式中h(j)為隱含層第j 個(gè)節(jié)點(diǎn)輸出值；ωij 為輸入層和隱含層連接權(quán)值；bj 為小波基函數(shù)hj 的平移因子；aj 為小波基函數(shù)hj 的伸縮因子；hj 為小波基函數(shù)。

本文采用的小波基函數(shù)為Morlet 母小波基函數(shù)，數(shù)學(xué)公式為：

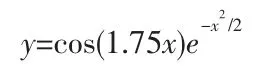
函數(shù)圖形如圖1：

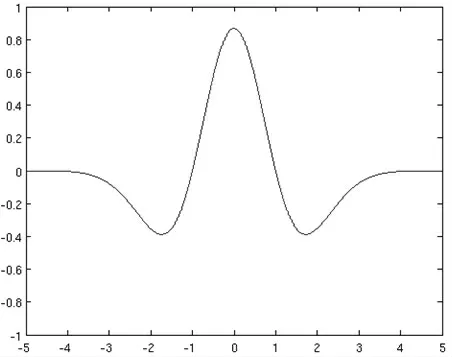
圖1

小波神經(jīng)網(wǎng)絡(luò)輸出層計(jì)算公式為：

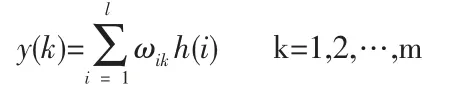
式中ωik為隱含層到輸出層權(quán)值；h(i)為第i 個(gè)隱含層節(jié)點(diǎn)的輸出；l為隱含層點(diǎn)數(shù)；m 為輸出層節(jié)點(diǎn)數(shù)。

1.2.2 小波神經(jīng)網(wǎng)絡(luò)參數(shù)修正

小波神經(jīng)網(wǎng)絡(luò)權(quán)值參數(shù)修正類似于BP 神經(jīng)網(wǎng)絡(luò)權(quán)值修正算法，采用梯度修正法修正網(wǎng)絡(luò)的權(quán)值和小波基函數(shù)參數(shù)，從而使小波神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)輸出不斷逼近期望輸出。修正過程如下：

（1）計(jì)算網(wǎng)絡(luò)誤差

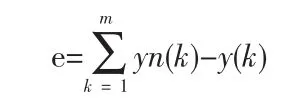
式中yn(k)為實(shí)際輸出；y（k）為小波神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)輸出。

（2）根據(jù)預(yù)測(cè)誤差e 修正小波神經(jīng)網(wǎng)絡(luò)權(quán)值和小波基函數(shù)系數(shù)

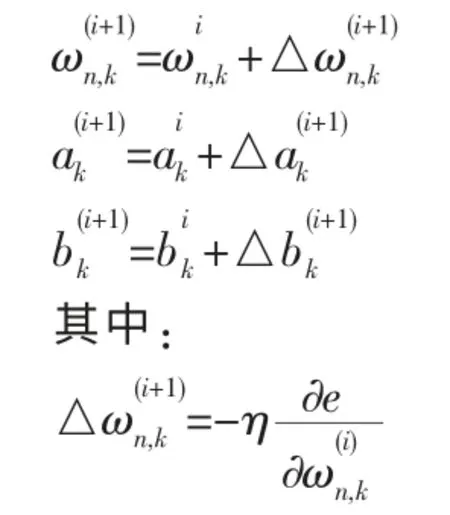
式中，η 為學(xué)習(xí)速率。

1.2.3 小波神經(jīng)網(wǎng)絡(luò)算法步驟

步驟1：網(wǎng)絡(luò)初始化。隨機(jī)初始化小波函數(shù)伸縮因子ak、平移因子bk以及網(wǎng)絡(luò)連接權(quán)值ωij、ωjk，設(shè)置網(wǎng)絡(luò)學(xué)習(xí)速率。

步驟2：計(jì)算預(yù)測(cè)輸出、網(wǎng)絡(luò)實(shí)際和預(yù)測(cè)誤差e。

步驟3：權(quán)值修正。根據(jù)誤差e 修正網(wǎng)絡(luò)權(quán)值和小波函數(shù)參數(shù)，使網(wǎng)絡(luò)預(yù)測(cè)值逼近實(shí)際值。

步驟4：判斷算法是否結(jié)束，如果沒有，返回步驟2。

1.3 小波神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)短時(shí)交通流量

（1）建立如圖1 所示神經(jīng)網(wǎng)絡(luò)模型。

（2）根據(jù)得到的交通流量數(shù)據(jù)樣本，進(jìn)行數(shù)據(jù)處理，并選擇一部分作為訓(xùn)練樣本，一部分為測(cè)試樣本。

（3）利用訓(xùn)練樣本對(duì)網(wǎng)絡(luò)進(jìn)行訓(xùn)練，隱含層函數(shù)采用小波函數(shù)。

（4）利用訓(xùn)練好的網(wǎng)絡(luò)進(jìn)行預(yù)測(cè)，并比對(duì)實(shí)際交通量。

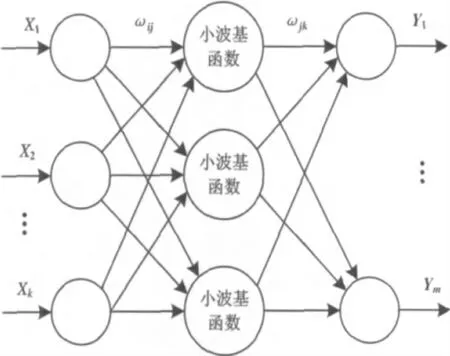
圖2 小波神經(jīng)網(wǎng)絡(luò)模型

2 實(shí)例分析

預(yù)測(cè)實(shí)例所采用的數(shù)據(jù)采自南京市交管局調(diào)查的某關(guān)鍵路段流量。有288+96 組數(shù)據(jù)樣本。其中每組數(shù)據(jù)間隔15min，前288 組用于訓(xùn)練網(wǎng)絡(luò)，后96 組用于測(cè)試網(wǎng)絡(luò)準(zhǔn)確性。

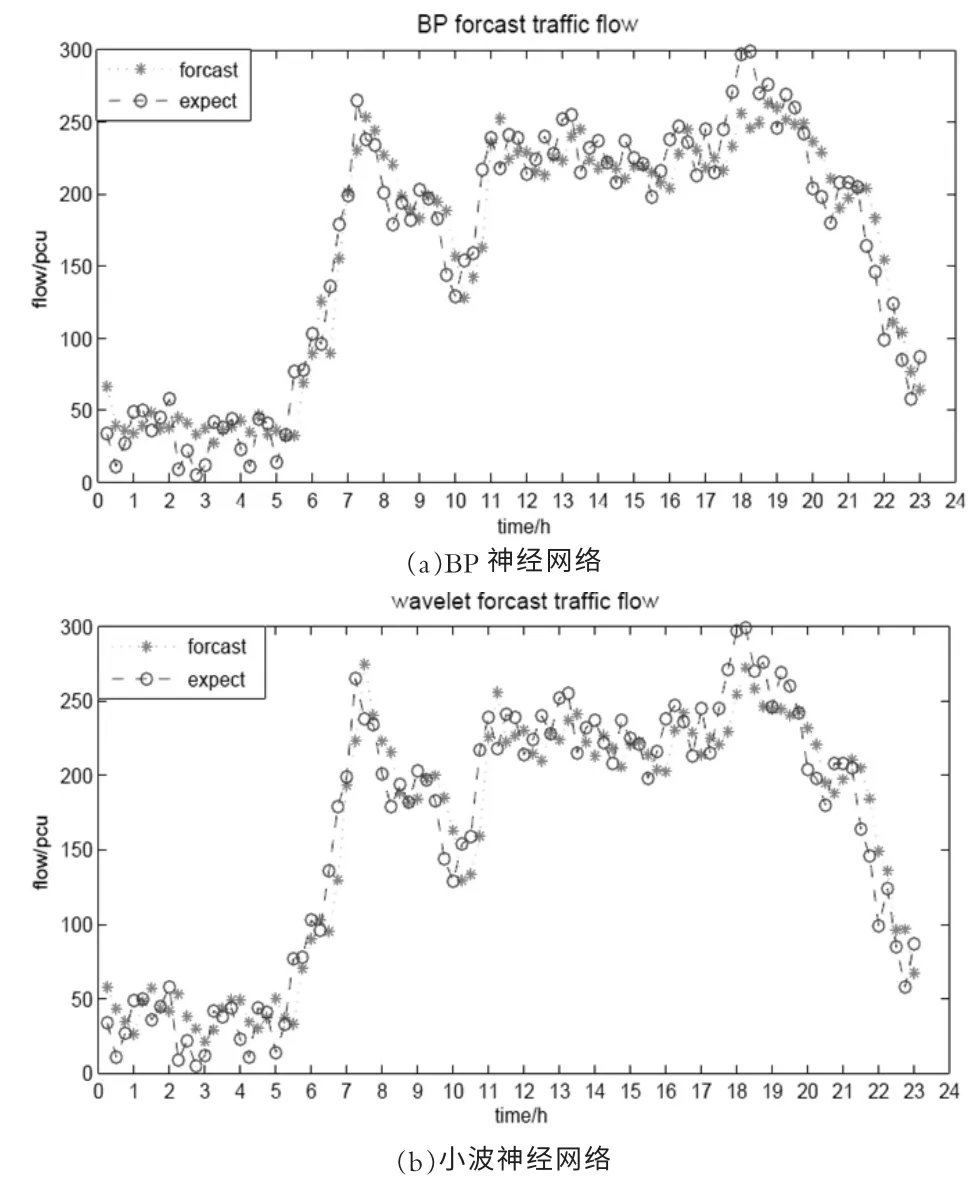
圖3 神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)輸出

2.1 BP 與小波神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)結(jié)果

傳統(tǒng)BP 神經(jīng)網(wǎng)絡(luò)目前已較為成熟[6]，構(gòu)建結(jié)構(gòu)為4-5-1 的三層BP 網(wǎng)，利用Matlab 神經(jīng)網(wǎng)絡(luò)工具箱newff、sim、train 三個(gè)主要函數(shù)進(jìn)行預(yù)測(cè)。由于是對(duì)比小波神經(jīng)網(wǎng)絡(luò)的準(zhǔn)確性，所以并沒有對(duì)這些函數(shù)的參數(shù)進(jìn)行討論和改變，均采用默認(rèn)值。小波神經(jīng)網(wǎng)絡(luò)設(shè)計(jì)三層網(wǎng)絡(luò)，分別為4 個(gè)節(jié)點(diǎn)的輸入層、6 個(gè)節(jié)點(diǎn)的隱含層、一個(gè)節(jié)點(diǎn)的輸出層。

根據(jù)上述理論，兩者預(yù)測(cè)流量與實(shí)際流量如圖3、預(yù)測(cè)誤差如圖4，誤差百分如圖5。

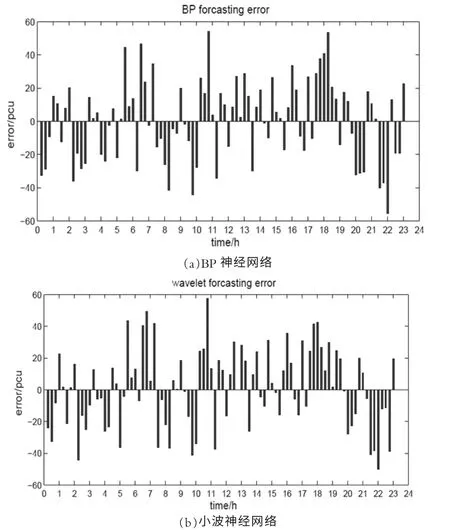
圖4 神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)誤差

圖5 神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)誤差百分比

2.2 預(yù)測(cè)準(zhǔn)確性分析

由兩種方法預(yù)測(cè)的流量對(duì)比實(shí)際流量分析可得，在6：00-22：00 這個(gè)時(shí)段預(yù)測(cè)較為準(zhǔn)確，這段時(shí)期相比其他時(shí)間段交通量較大，是人們出行活動(dòng)的主要時(shí)期，在這個(gè)時(shí)間段預(yù)測(cè)準(zhǔn)確是至關(guān)重要的。夜間（22：00-6：00）這段時(shí)期可能車流較少，隨機(jī)性較大，造成預(yù)測(cè)的誤差加大。本文沒有更多數(shù)據(jù)檢驗(yàn)，實(shí)為一種遺憾。綜上來看，神經(jīng)網(wǎng)絡(luò)在預(yù)測(cè)短時(shí)交通流時(shí)具有較高的準(zhǔn)確性。

定性的分析預(yù)測(cè)方法的準(zhǔn)確性還不夠，為了檢驗(yàn)各種方法的預(yù)測(cè)精度，本次案例誤差結(jié)果對(duì)比指標(biāo)采用平均絕對(duì)誤差（mean absolute deviation，MAD，表示預(yù)測(cè)值與實(shí)測(cè)值得實(shí)際偏差絕對(duì)值的均值）、平均絕對(duì)百分比誤差（mean absolute percentage error，MAPE，表示預(yù)測(cè)值與實(shí)測(cè)值得實(shí)際偏差絕對(duì)值占實(shí)測(cè)值百分比的均值）。

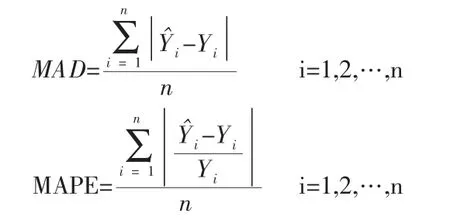
MAD 與標(biāo)準(zhǔn)偏差類似，但更容易求的。MAD 能較好的反映預(yù)測(cè)的精度，但它不容易衡量無偏性。MAD 與MAPE 常用來衡量預(yù)測(cè)誤差，但單一的指標(biāo)很難全面地評(píng)價(jià)一個(gè)預(yù)測(cè)模型，所以本次這2 個(gè)指標(biāo)全部選用來檢驗(yàn)預(yù)測(cè)精度。

本次BP 神經(jīng)網(wǎng)絡(luò)和小波神經(jīng)網(wǎng)絡(luò)的MAD 與MAPE 指標(biāo)如表1 所示。

由表1 可以看出，兩種方法預(yù)測(cè)的交通量誤差在20 左右，相比人們活動(dòng)時(shí)期的交通量不算太大，MAPE 如此高是由于部分時(shí)間車流較小，預(yù)測(cè)誤差百分比很容易超過1。總體來說小波神經(jīng)網(wǎng)絡(luò)優(yōu)于BP 神經(jīng)網(wǎng)絡(luò)，但優(yōu)勢(shì)不明顯，可選用其他母小波做隱含層基函數(shù)或使用增加動(dòng)量項(xiàng)修正網(wǎng)絡(luò)參數(shù)的算法，來提高網(wǎng)絡(luò)學(xué)習(xí)效率。

3 結(jié)論

本文主要分析了小波變換的特點(diǎn)、原理，并以Morlet 母小波作為神經(jīng)網(wǎng)絡(luò)隱含層基函數(shù)構(gòu)建了小波神經(jīng)網(wǎng)絡(luò)，對(duì)數(shù)據(jù)進(jìn)行預(yù)測(cè)分析，并比對(duì)了傳統(tǒng)的BP 神經(jīng)網(wǎng)絡(luò)，發(fā)現(xiàn)神經(jīng)網(wǎng)絡(luò)作為一種新型預(yù)測(cè)技術(shù)，具有一定的準(zhǔn)確性，但無論是BP 神經(jīng)網(wǎng)絡(luò)還是小波神經(jīng)網(wǎng)絡(luò)都不夠完善[7]，短時(shí)交通流預(yù)測(cè)作為未來交通管理的基礎(chǔ)，今后還應(yīng)有越來越多的神經(jīng)網(wǎng)絡(luò)模型應(yīng)用在交通流預(yù)測(cè)上，發(fā)展更適合的算法以得到更準(zhǔn)確的預(yù)測(cè)結(jié)果。

［1］孫湘海，劉潭秋.基于非線性時(shí)間序列模型的城市道路短期交通流預(yù)測(cè)研究[J].土木工程學(xué)報(bào)，2008(1)：104-109.

［2］邵春福，熊志華，姚智勝.道路網(wǎng)短時(shí)交通需求預(yù)測(cè)理論、方法及應(yīng)用[M].北京：清華大學(xué)出版社，2011.

［3］沈穎潔，韓寶睿，劉英麗，等.基于仿真的隧道檢測(cè)器優(yōu)化布設(shè)及短時(shí)交通流預(yù)測(cè)[J].公路交通科技，2014，1：124-130.

［4］蔡念，胡匡祜，李淑宇，等.小波神經(jīng)網(wǎng)絡(luò)及其應(yīng)用[J].中國體視學(xué)與圖像分析，2001，12(4)：239-245.

［5］侯霞.小波神經(jīng)網(wǎng)絡(luò)若干關(guān)鍵問題研究[D].南京航空航天大學(xué)，2006.

［6］王吉權(quán).BP 神經(jīng)網(wǎng)絡(luò)的理論及其在農(nóng)業(yè)機(jī)械化中的應(yīng)用研究[D].沈陽農(nóng)業(yè)大學(xué)，2011.

［7］田晶，楊玉珍，陳陽舟.短時(shí)交通流量?jī)煞N預(yù)測(cè)方法的研究[J].公路交通科技，2006（4）：104-106.