密頻結構實模態參數的特征曲線法
張 淼
在結構振動分析中,經常需要求解廣義特征問題Kφ=λMφ,其中K和M是結構的質量和剛度矩陣,λ為特征值,φ為特征向量。求解特征值問題,即為求解結構的固有頻率和振型,在工程實際應用及求解結構動力響應方面都具有重要的意義[1-2]。特征值即為結構的無阻尼固有頻率(實頻率),特征向量即為結構的無阻尼固有振型(實模態),再加上阻尼比,在工程中統稱為實模態參數。一個結構的動力特性可以用它的實模態參數進行完整的描述,因此對它們的研究伴隨著工程應用的設計、分析、修正、損傷識別等各個環節。若特征值和特征向量在設計參數的某可行域內或局部發生了轉向和彎曲,表明結構對該設計參數是敏感的,尤需關注的是,結構很可能產生密頻或重頻現象[3],從而為結構的穩定性帶來隱患。特征對發生變化的測量方式之一是其導數,工程中稱為靈敏度[4],它們可在數值上反映變化的位置及彎曲發生的程度等。因此,特征曲線法的應用可以在很大程度上使設計工作遠離可能產生危險的假定模型,在工程上具有良好的應用價值。
1 特征值分析
對N自由度的線性離散振動系統的運動方程為

式中M,C和K∈RN×N分別為系統的質量、阻尼和剛度矩陣。作拉普拉斯變換x(t)=uewt=ueiwt(w=iω)代入(1)式可得(w2Mu+wCu+Ku)ewt=0。令C=0,則無阻尼固有頻率與規范化實模態為(ω2,φi)(i=1,2,…,N,w2=-ω2=λ),滿足特征方程

實際上特征方程(2)是關于矩陣M和K的廣義特征問題。λi為固有頻率(也可稱為特征值),φi為無阻尼正則實模態(也可稱為特征向量)。
考慮如下弱耦合系統[5],這是一個由兩個彈性元件k1和k2及兩個質量塊m1和m2構成,并用一個弱彈性元件k聯接的兩自由度系統,假定只在x軸方向上發生振動,見圖1。
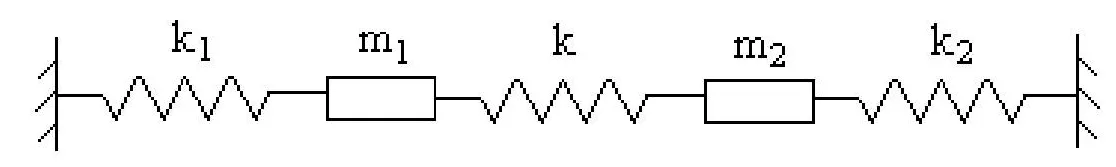
圖1 弱耦合系統示意圖
特征方程


其中 p=m1m2,h=-(k1+k)m2-(k2+k)m1,c=k1k+k1k2+k2k.
令m1=m2=1,k2=1,而取設計參數為k1,其變化區間取為0.6至1.4,分別在k=0.05及k=0.01兩種情況下用MATLAB繪制λ1和λ2關于設計參數k1的關系圖(圖2)。
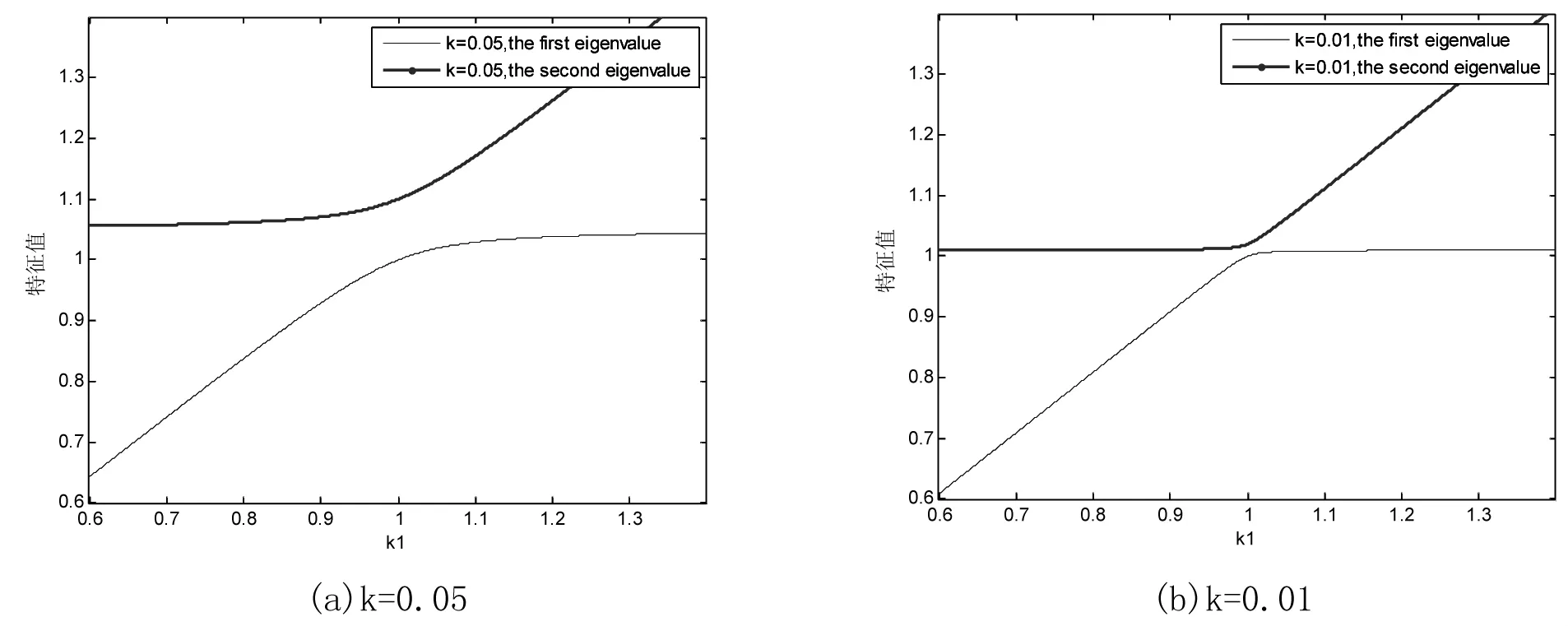
圖2 特征值函數的關系圖
由圖2分析可知,首先對不同的k值,系統均在k1=1處發生兩個特征值接近(密頻)的現象,即在k1=1的鄰域內出現了密頻現象,而對k=0.01時更加接近一些,這說明更小的值會加重密頻現象的發生。其次,兩個特征值曲線均在k1=1處發生了彎曲與轉向,k的取值越小,彎曲發生得越劇烈。
對公式(4)直接求導得兩個特征值的一階靈敏度為
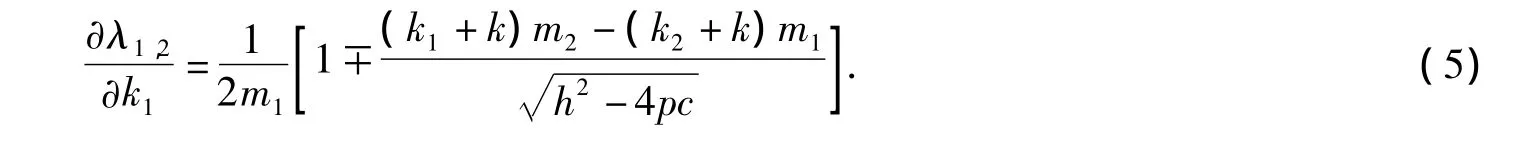
用MATLAB繪制λ1和λ2關于設計參數k1的一階靈敏度關系圖(圖3)。

圖3 特征值一階靈敏度的關系圖
由λ1的一階靈敏度分析可知,在k1∈[0.6,0.9]內,λ1以幾乎恒定的變化率增加;到k1=1附近時,變化率發生了較大變動,從1迅速地減少到0左右,其后不再發生大的變化,說明特征值λ1由與設計參數同步增加迅速地轉變為與設計參數無關,只穩定在固定值。由λ2的一階靈敏度分析可知,在k1∈[0.6,0.9]內,λ2變化率幾乎為0,反映了λ2在此范圍內不發生大的變化;到k1=1附近時變化率也發生了較大變動,從0迅速地增加到1左右,其后不再發生大的變動,說明λ2由穩定值迅速地轉變為與設計參數的增加而同步增加。以上說明,兩條特征值曲線均在k1∈[0.9,1.1]范圍附近發生了劇烈的轉向和彎曲,而且k的取值越小,彎曲發生得越劇烈。這一分析與圖2的分析結果一致,可見靈敏度分析確實能反映系統的原始動特性。
2 特征向量分析
相應地,規范化特征向量為
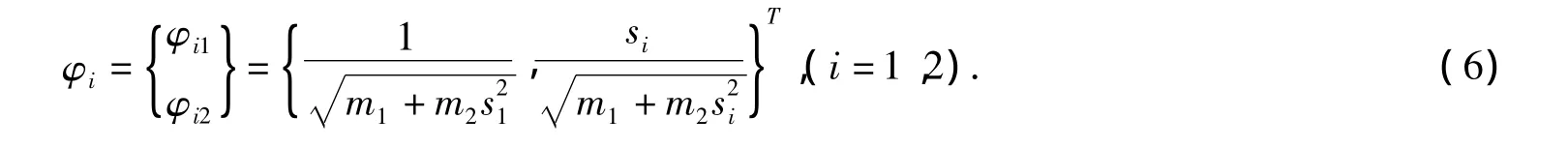
用MATLAB繪制φ1和φ2關于設計參數k1的關系,見圖4和圖5。
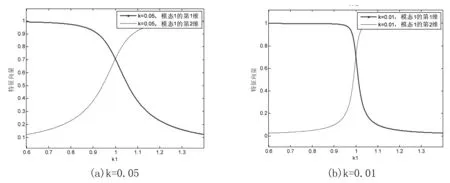
圖4 φ1關于設計參數k1的關系圖
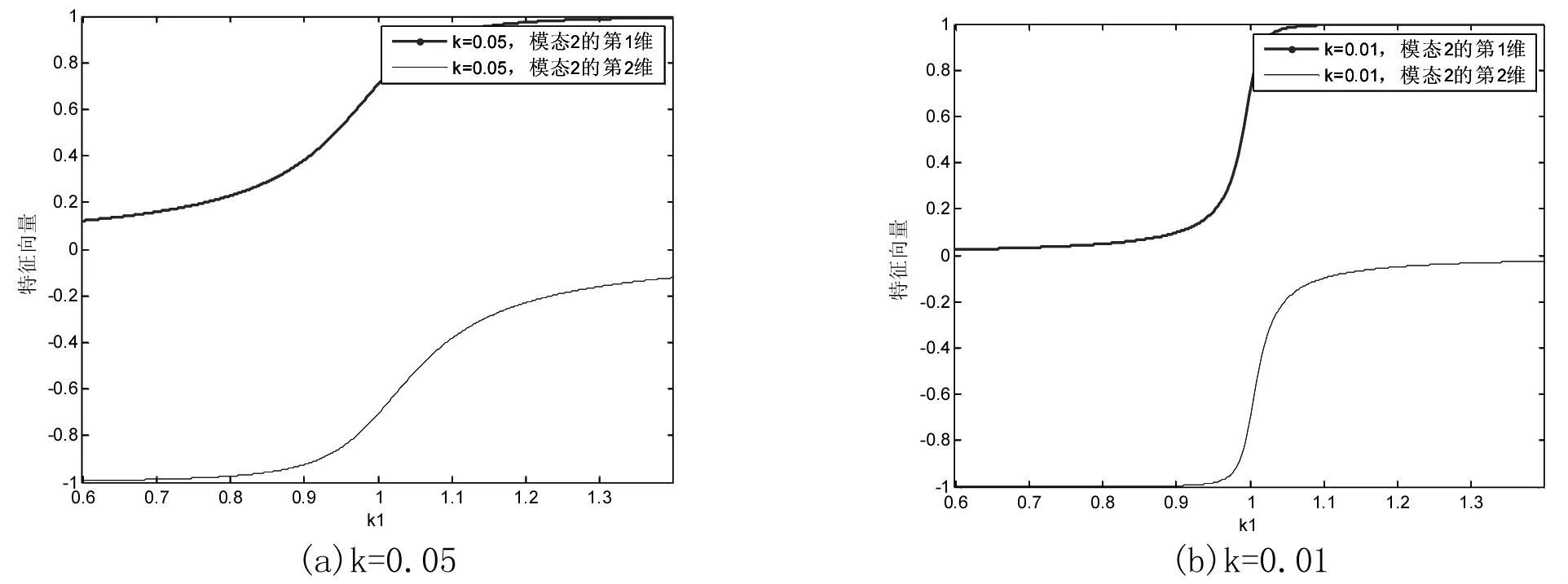
圖5 φ2關于設計參數k1的關系圖
對不同的k值,模態1的第1維分量與第2維分量均在k1=1附近發生了轉向,且變化劇烈。在k1=1的小幅變化范圍內,k的取值越小,模態1所發生的變化越劇烈。這說明模態1的不穩定性發生在密頻點k1=1處。同樣地,對不同的k值,模態2的第1維分量與第2維分量均在k1=1附近發生了轉向,且變化劇烈。模態的不穩定性也發生在密頻點k1=1處。從前文的分析可知,由于k取值越小,顯示結構密頻的程度越高,因此圖4和圖5反映的是密頻的程度越高,模態的跳躍性越強。
用公式(6)式直接求導得兩個特征向量的一階靈敏度為
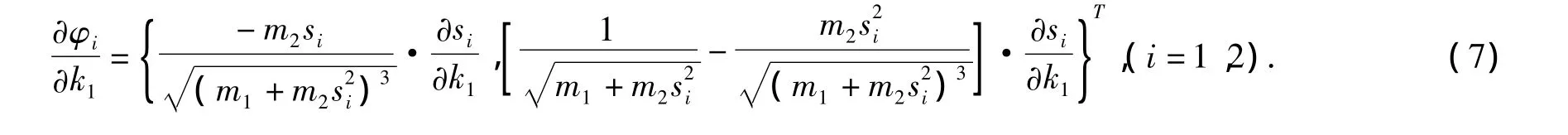
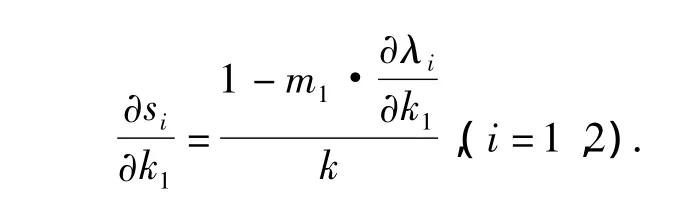
用MATLAB繪制φ1和φ2的第1維分量關于設計參數k1的一階靈敏度關系見圖6。
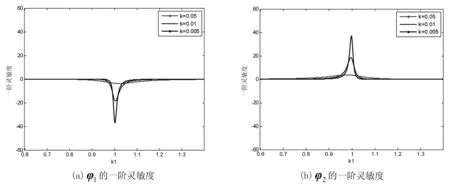
圖6 不同k值時φ1和φ2的第1維分量關于設計參數k1的一階靈敏度對比圖
圖6僅以模態1和模態2的第1維分量為研究對象,圖形顯示,這兩個模態的第1維分量均在k1∈[0.6,0.9]范圍左右變化率幾乎為0,說明模態此時隨設計參數的變化不大,較為穩定;但在k1∈[0.9,1.1]范圍附近,變化率發生了較大的變動,其中k值越小,變化率變化的幅度越大,顯示出模態在這個范圍內發生了一定程度的跳躍;然后變化率又幾乎為0,模態又呈現出穩定狀態。這一分析結果與圖4和圖5的分析結果一致。
3 結語
本文針對一個弱耦合系統,首先利用特征值及特征向量與設計參數的關系圖,來分析設計參數對系統狀態的影響,尤其是發生密頻現象時,密頻現象對結構可能產生的破壞作用進行了分析;再利用特征值與特征向量關于設計參數的靈敏度曲線圖,來分析和驗證上述結果,表明特征對靈敏度分析確實能在很大程度上反映結構性態。同時說明在工程實踐中若沒有條件獲得足夠的結構原始實模態參數信息,卻僅憑其導數信息,也可判斷和預知那些隱藏的信息,在一定程度上能夠節省研究和設計的成本。
[1]張淼,鞠偉.計算各種振系模態靈敏度的統一算法[J].長春工程學院學報:自然科學版,2012,13(4):119-122.
[2]于瀾.模態參數的靈敏度分析在結構工程領域中的應用[J].長春工程學院學報:自然科學版,2012,13(3):1-3.
[3]張淼.基于松馳技術的重頻密頻結構模態靈敏度分析[J].合肥工業大學學報:自然科學版,2012,35(12):1605-1609.
[4]于瀾,張淼,鞠偉,等.非保守系統復模態的規范正交性及其應用[J].華南師范大學學報:自然科學版,2013,45(4):21-24.
[5]于瀾,張文丹,付向南.非對稱重頻阻尼系統狀態向量的攝動分析[J].長春理工大學學報:自然科學版,2011,34(3):170-172.

