模糊加權平均決策模型的結構元求解方法

宮 莉

加權平均在評價決策、工程管理、經濟統計等方面有廣泛的應用，如決策模型的求解、質量控制等.如果對象的評價值或權重的界限表現不確定，為使決策者以及評價對象本身所具有的模糊性能有效地利用起來，進行綜合評價，可以把它們表達成模糊數，進行模糊加權平均，其輸出結果就包含有更多的信息，表明了評價結果的各種可能性，為決策者提供更好的依據和參考，對此，文獻［1－2］進行了模糊綜合評判，但評價結果是各方案滿足總目標的隸屬函數值，本質上也是一個確定值.BUCKLY、值田等利用模糊集合［3－4］處理類似問題.近些年來，許多學者都對此方面進行了相關研究［5－9］.

目前的論文在利用模糊加權平均法求解決策模型［10］時，大多忽略了模型中系數之間的限定運算問題，求解結果使人難以信服.針對此問題，本文結合模糊結構元理論［11］，首先對模糊加權平均的運算問題進行討論，然后在此基礎上給出了一種隨機模擬的求解方法，有效地解決了決策模型中系數的限定性運算問題，便于應用，值得進一步研究推廣.

1 模糊數運算及結構元表示

定義1［12］對于模糊集∈F(R)，稱為R上的有界閉模糊數當且僅當滿足:(1)是正規的，即存在∈R，使得()=1;(2)對于 λ∈(0，1］，={x|(x)≥λ}是閉區間;(3)為有界.記R上的有界閉模糊數全體為F(R).

定義2［13］設E為實數域R上的模糊集，隸屬函數記為E(X)，x∈R.如果E(x)滿足下述性質:(1)E(0)=1;(2)在區間［－1，0)上E(x)是單增右連續函數，在區間(0，1］上E(x)是單降左連續函數;(3)當－∞ ＜x＜－1或者1＜x＜∞時，E(x)=0.則稱模糊集E為R上的模糊結構元.

定理1［13］對于給定的一個正則模糊結構元E和任意的有限模糊數，總存在一個在［－1，1］上的單調有界函數f，使得=f(E).嚴格地說，存在f的集值延拓，使得=(E)，并稱模糊數是由模糊結構元生成的.

定理2［13］若模糊數=f(E)，則的隸屬函數為E(f－1(x))，這里 f－1(x)關于變量 x和 y的輪換對稱函數(若f(x)是連續嚴格單調的，則f－1(x)是f(x)的反函數).

若D［－1，1］為區間［－1，1］上同序單調函數全體，定義D［－1，1］上的同序單調變換:

其中 fτ0(x)=f(x)，fτ1(x)=－f(－x)，fτ2(x)=(f(－x)≠0)，fτ3(x)=－(f(x)≠0)(x∈［－1，1］).

定理3［13］設 E 為對稱模糊結構元，f和 g 是［－1，1］上的同序單調有界函數，模糊數=f(E)，=g(E)，則有:(1)+=f(E)+g(E)=(f+g)(E);(2)－=f(E)－g(E)=(f+gτi)(E);(3)=f(E)g(E)(fg)(E);當 k 為非負實數時，k=(kf)(E);(4)=f(E)gτ2(E)=(fgτ2)(E).

上述定理證明可參考文獻［11－13］.

2 基于結構元理論的模糊加權平均的運算

證明 對于v∈V有

根據Zadeh的擴張原理，對于任意t∈R有

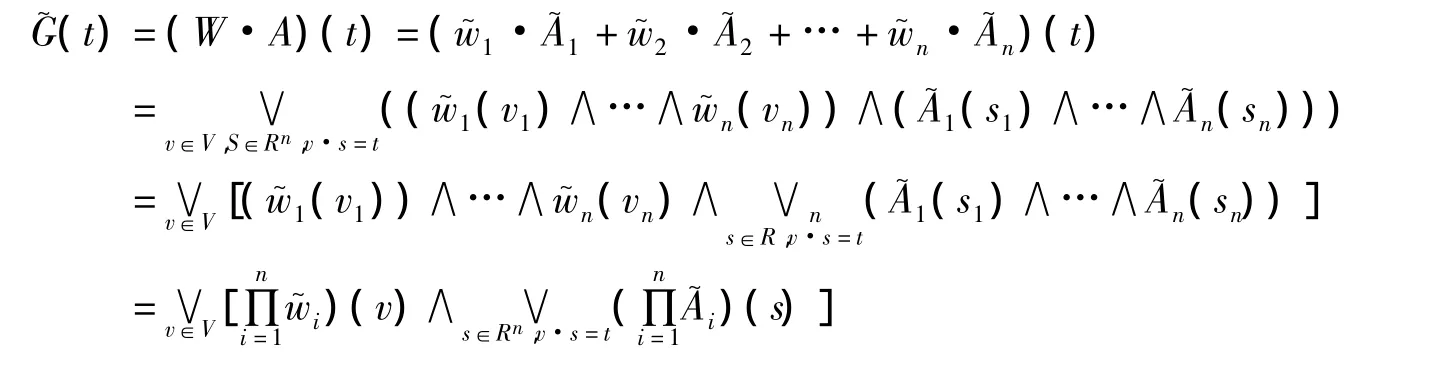
下面證明多元函數 h(v，t)=(v·A)(t)，v∈V，t∈R 是一致連續的.實際上，記 Xv，t={X∈Rn|v·x=t}，則h(v，t)=或 h(v，t)

類似f(v)一致連續性證明，易A(x)證在Rn上一致連續，而Xv，t表示Rn中的連續超平面，對于任意v∈V，根據數學分析的知識，知h(v，t)關于變量t在R上的連續凸函數.同理，可知對于任意t∈R，h(v，t)為關于變量v在V上的連續凸函數.故h(v，t)在v×R上一致連續.

其隸屬函數為

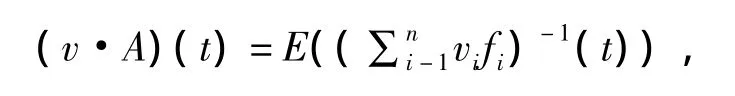
所以

3 模糊加權平均決策模型的結構元解法

結合模糊加權運算的結構元理論，來求解模糊加權決策模型，提出一種隨機模擬的算法來進行求解，這里給出具體的算法步驟，具體如下:

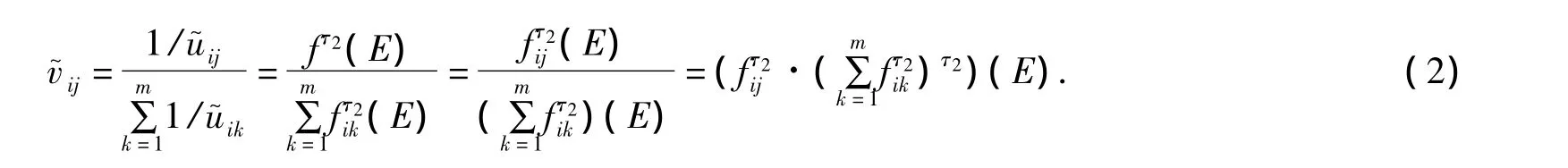
規范化公式為

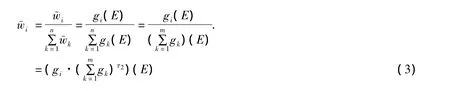
其中，i=1，2，…，n.

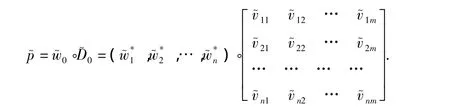
模糊合成算子有很多，根據不同情況選擇相應的算子.最常用的模糊合成算子是加權平均，即

根據 qj，j=1，2，…，n 值的大小確定 U 中方案的優劣排序，規則:若 qi≥qj，那么 uiuj，即方案 ui優于方案uj.

若直接利用式(2)代入

計算P值.由于V中的點連續且式中存在連續積分，直接計算運算量很大，需采用數值計算的方式進行近似計算.簡化的方法:對V和連續積分進行離散化，用其近似形式代替.設V離散后V'={vk|vk∈V，k=1，2，…，N1}.記離散后的P值為P'.實際上，只要V'中的點在V上分布得足夠均勻、點足夠多，P'值就能以足夠的精度靠近P.

對于如何得到V'，這里提供一種隨機數生成的方法:首先，隨機生成一個N×n矩陣T=［tij］N×n，其中tij是［0，1］之間的隨機數;其次，對矩陣T的行向量進行歸一化，設歸一化后的隨機矩陣為T'=［t'ij］N×n，其中隨機矩陣的行向量便組成了V'.易知，V'中的點均勻分布于V上.

4 數值實例

某單位在對干部進行考核選拔時，制定了6項考核指標(因素):思想品德f1、工態f2、工作作風f3、文化水平和知識結構f4、領導能力f5和開拓能力f6，通過群眾推薦和評議，對各項指標分別打分，再進行統計處理，從中確定了5名候選人ui(i=1，2，3，4，5).由于群眾對同一候選人所給出的指標值(狀態值)并不完全相同，因此經過統計處理后的每個候選人在各因素下的狀態值是以三角模糊數形式給出的，屬性值均為越大越好的效益型，具體的屬性值見表1.

表1 候選人在各因素下的屬性值及各因素的權重

步驟1 決策矩陣的結構元表示及其規范化.根據表1，容易確定模糊決策矩陣=［］5×6，其中表示對象uj在因素fi下的屬性值.由于中每個元素均為三角模糊數，而三角模糊數結構元表示形式為=［aij，bij，cij］=fij(E).其中，fij(x)根據式(2)，得到的規范化矩陣=［gij(E)］5×6，其中 gij(x)=fij(x)·(∑(－x))－1.

步驟2 模糊權重的結構元表示及其規范化.這里模糊權重向量

類似于步驟1或(3)式，對W的規范化，得到規范化向量W*.

步驟3 計算P=(p1，p2，p3，p4，p5).這里在近似計算pi值時，V'的隨機實值權重向量數N1=1000，數值積分采用梯形數值積分(trapz()函數)，然后，利用編程計算得到表2.

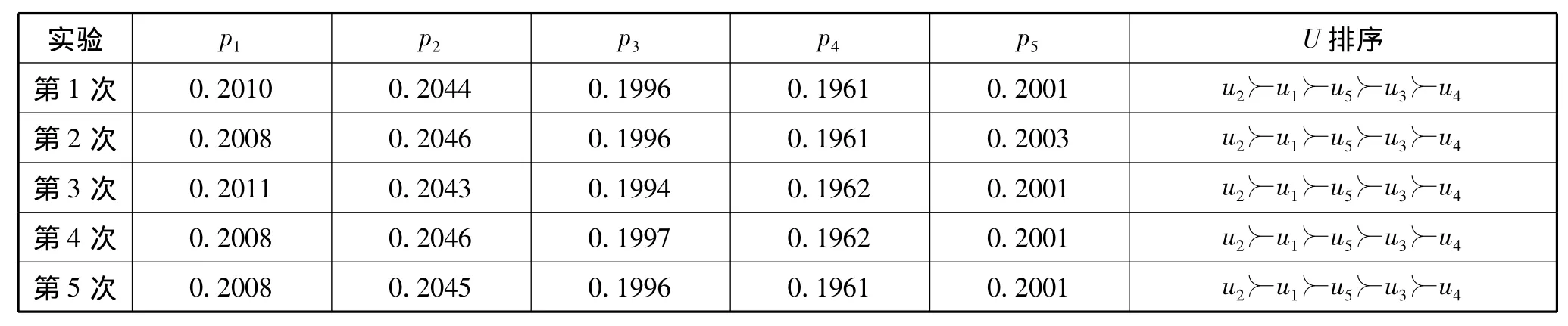
表2 基于隨機模擬下的決策排序

步驟4根據pi值大小對5個候選人進行排序結果:u2u1u5u3u4.

5 結語

本文首先結合模糊結構元理論，對模糊加權平均數的運算及其相關性質進行了探討與研究，并給出具體的證明，然后在此基礎上提出了一種隨機模擬算法，用以求解模糊加權平均決策模型，并結合模型給出了具體的求解步驟，有效地解決了模型求解過程中參數的限定性運算問題，最后通過數值實例對文中的結論進行了證明.

［1］張躍，鄒壽平，宿芬.模糊數學方法及其應用［M］.北京:煤炭工業出版社，1992.

［2］陳湛勻.現代決策分析概論［M］.上海:上海科學技術文獻出版社，1991.

［3］植田等.商品評價中AHP與Fuzzy AHP的比較研究［C］∥日本經營工學會平成2年春季大會論文集，1990:127－128.

［4］Buckley J J.Fuzzy hierarchical analysis［J］.Fuzzy Sets and Systems，1985，17(2):233－247.

［5］Xu R N，Zhai X Y.Fuzzy logarithmic least squares ranking method in analytic hierarchy process［J］.Fuzzy Sets and Systems，1996(77):175－190.

［6］Chang D Y.Applications of the extent analysis method on fuzzy AHP［J］.European Journal of Operational Research，1996(95):649－655.

［7］姚敏，張森.模糊一致矩陣及其在軟科學中的應用［J］.系統工程，1997，15(2):54－57.

［8］Kwiesielewicz M.A note on the fuzzy extension of Satty＇s priority［J］.Fuzzy Sets and Systems，1998(95):161－172.

［9］Chen CT.Extensions of the TOPSIS for group decision－making under fuzzy environment［J］.Fuzzy Sets and Systems，2000(114):1－9.

［10］徐澤水.對方案有偏好的三角模糊數型多屬性決策方法研究［J］.系統工程與電子技術，2002，24(8):9－12，20.

［11］郭嗣琮.模糊分析中的結構元方法(I)，(II)［J］.遼寧工程技術大學學報，2002，21(5):670－673;21(6):808－810.

［12］郭嗣琮.［－1，1］上同序單調函數的同序變換群與模糊數運算［J］.模糊系統與數學，2005，19(3):105－110.

［13］郭嗣琮，蘇志雄，王磊.模糊分析計算中的結構元方法［J］.模糊系統與數學，2004，18(3):68－75.