人工魚群和蒙特卡羅混合算法的應用*

李軍民，李立博

(西安科技大學 計算機科學與技術學院，陜西 西安710054)

0 引 言

人工魚群算法繼承了基本魚群算法的特性:從人工魚個體的最底層尋優到整個魚群的全局尋優。目前人工魚群算法在數值計算方面，已經由解決一維靜態優化問題發展到解決二維甚至更高維的動態組合優化問題，其特點就是無需借助目標函數的梯度值等信息，僅使用目標函數的函數值，在搜索全局最優解的過程中具有一定的自適應能力。特別是人工魚群算法對初值無要求、參數的選擇在某種程度上也不敏感，使得算法更加具有并行、全局、快速、跟蹤等特點。該算法已經廣泛應用到通信［1-3］、神經網絡、數據挖掘、控制、交通等領域，同時為NP 類問題、參數優化［4］、數值求解［5-7］、模型求解等問題［8-10］提供了很好的求解途徑。

蒙特卡羅算法［11-12］不同于求解確定性數值解的一些算法，它是從問題的相反關系出發，用于解決數學［13］、物理問題的不確定性數值解，其基本思想是:在概率統計層面尋找一個相似體，通過實驗取樣的方法獲得相似體的近似解來解決數學、物理問題。采用基于蒙特卡羅算法的蒙特卡羅試驗取代部分真實試驗，節省了設計的完成時間和工作量，從而促進解決了概率以及數值解問題的發展。

二重積分作為科學計算中一類相對重要的積分，人們一直追求如何方便快快地使用計算機程序求解其數值解。結合近幾年比較經典的智能優化算法—人工魚群算法和熟知的蒙特卡羅算法求解二重積分的數值解，將蒙特卡羅算法求解二重積分數值解的思想引入到人工魚群算法中，改進了人工魚群算法中的適應度函數和積分求和式［14-17］。計算結果表明:采用混合算法和其他算法相比較，二重積分數值解的精確度有所提高。

1 人工魚群和蒙特卡羅的混合算法

采用人工魚群算法求解二重積分的數值解，是基于被積函數的凹凸形狀來隨機的劃分積分區域，其思路是:首先在二重積分的積分范圍內任意生成指定數目的點;然后按照一定的規則，采用人工魚群算法對其進行優化，從而更好地求解二重積分的數值解，并克服傳統的求二重積分方法中的不足。

應用蒙特卡羅方法來求二重積分的數值解，其中心思想是:序列化積分區域中產生的非均勻隨機點，將被積函數所對應的隨機變量的算術平均值視為其積分的近似值，即

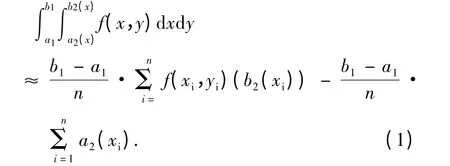
結合人工魚群算法和蒙特卡羅方法，來求解二重積分的數值解，主要是針對文獻［14］中人工魚群算法的適應度函數和積分求和公式進行改進(分別參見2)和7))，引入蒙特卡羅求積分的思路。既保留其各自算法的優點，又節省計算時間、提高計算精度、算法的收斂性較好，同時相對蒙特卡羅方法減少節點數目。

設關于x，y 的二元函數f(x，y)為區域D:a1≤x≤b1，a2(x)≤y≤b2(x)上滿足蒙特卡羅算法條件的有界函數［2］，采用混合人工魚群和蒙特卡羅算法求函數f(x，y)在區域D 上的二重積分的數值解的步驟如下

1)算法開始，設定人工魚群算法的參數，初始化人工魚;

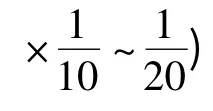
2)計算每條人工魚的適應度函數值，更新公告板;不同于文獻［1］該算法中人工魚的適應度函數為

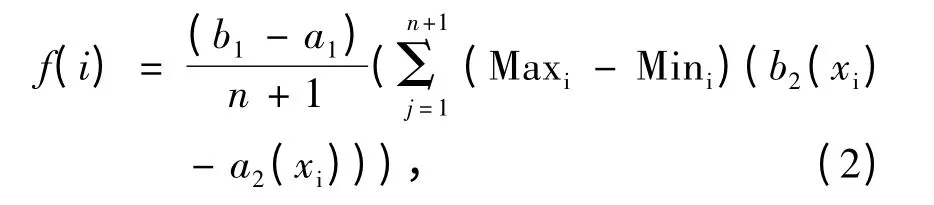
計算積分區域D 劃分成的每個小矩形的4 個頂點和矩形中心對應的函數值，并找出這5 個函數值中的最小值Mini和最大值Maxi. 在這里若函數f(i)的值越趨于0，則表示該人工魚個體(即該分割方法)越優［14］。

3)模擬執行追尾、聚群行為，選擇優的行為作為人工魚的前進方向;

4)如果2 個行為都沒有改進，則執行覓食行為;

5)重復2);

6)判斷是否滿足結束條件:是繼續7)，否轉2);

7)計算二重積分的數值解并輸出結果，算法結束。

文中的積分求和公式，參照蒙特卡羅算法表示為

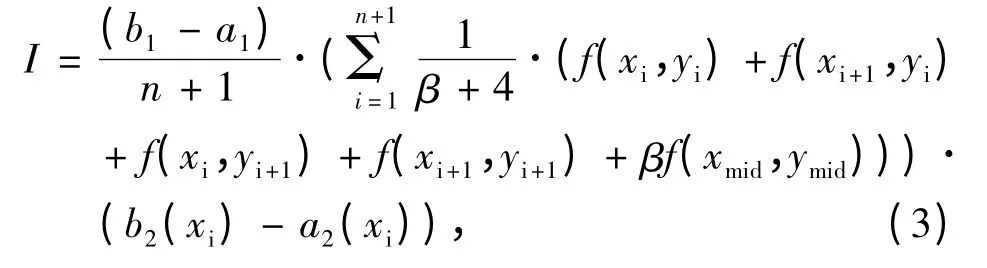
其 中 f(xi，yi)，f(xi+1，yi)，f(xi，yi+1)，f(xi+1，yi+1)，f(xmid，ymid)分別為積分區域D 劃分成的小矩形的4 個頂點和矩形中心對應的函數值［14］，β = 8.

2 示例演算

已知這個二重積分的準確值為5.100 170 0，在(0.0)點被積函數無定義，當變量x 方向趨近下限時，函數圖形變化劇烈。文中算法的參數設置為

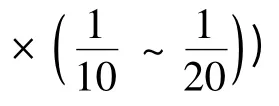
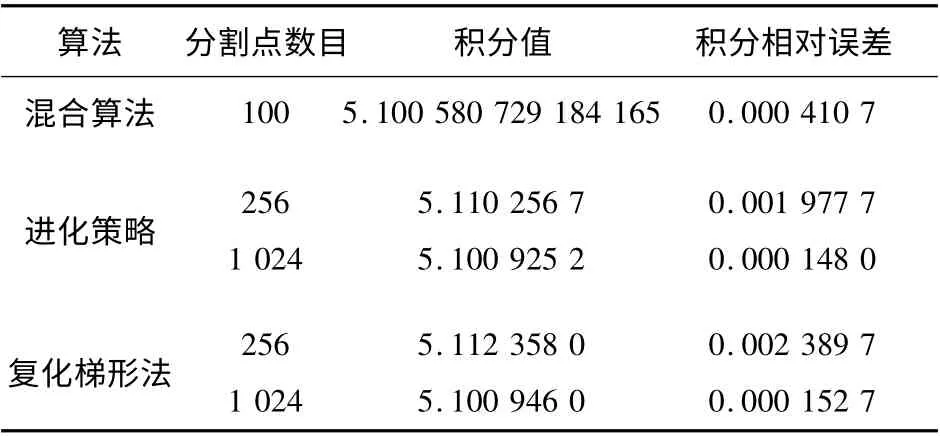
表1 幾種算法的積分值及相對誤差Tab.1 Integral value and the relative error of several algorithms

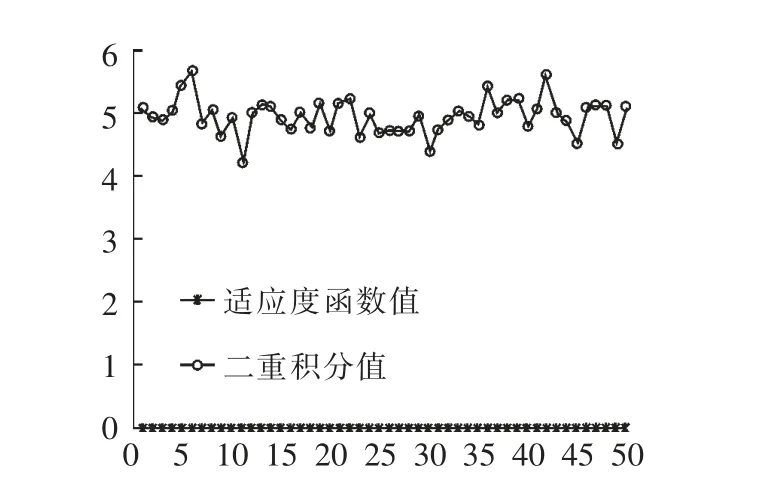
圖1 適應度函數值和迭代次數、二重積分值和迭代次數的關系曲線Fig.1 Relation curves fitness function value and the number of iterations，the curve of double integral value and number of iterations

3 結 論

使用計算機方便快捷的求解二重積分的數值解，在數學問題領域中一直占據不可或缺的地位。將蒙特卡羅求解二重積分數值解的思想引入到人工魚群算法中，改進人工魚群算法中的適應度函數和積分求和公式的人工魚群和蒙特卡羅混合算法更加有利于二重積分的數值解求解方法的發展。

在采用人工魚群算法和蒙特卡羅的混合算法求二重積分時，適應度函數值相對趨近于0，二重積分值也基本收斂于積分值，分割點數目為100時，誤差已經是0.000 410 7. 實驗表明，文中提出的混合改進算法在一定程度上使得分割點的數目得以減少，收斂的速度和計算的精度也有所提高。

References

［1］ 王軍偉，王興偉，黃 敏.一種基于禁忌人工魚群算法的智能QoS 組播路由算法［J］.小型微型計算機系統，2009，30(9):1 720 -1 723.WANG Jun-wei，WANG Xing-wei，HUANG Min. Tabu artificial fish swarm algorithm based intelligent QoS multicast routing algorithm［J］.Journal of Chinese Computer Systems，2009，30(9):1 720 -1 723.

［2］ 羅景峰，王瑩瑩.基于魚群算法的全終端網絡可靠性優化設計［J］.微電子學與計算機，2009，26(2):93 -96.LUO Jing-feng，WANG Ying-ying. Optimization design of ALL-terminal networks reliability base on fish-wwarm algorithms［J］.Microelectronics and Computer，2009，26(2):93 -96.

［3］ 王興偉，秦培玉，黃 敏.基于人工魚群的ABC 支持型QoS 單播路由機制［J］.計算機學報，2010，33(4):718 -725.WANG Xing-wei，QIN Pei-yu，HUANG Min. ABC supporting QoS unicast routing scheme based on the Artificial Fish Swarm［J］. Chinese Journal of Computers，2010，33(4):718 -725.

［4］ 王錫淮，鄭曉鳴，肖健梅.求解約束優化問題的人工魚群算法［J］.計算機工程與應用，2007，43(3):40 -42.WANG Xi-huai，ZHENG Xiao-ming，XIAO Jian-mei.Artificial fish-swarm algorithm for solving constrained optimiza-tion problems［J］. Computer Engineering and Applications，2007，43(3):40 -42.

［5］ 周永權，張明，趙 斌.基于進化策略方法求任意函數的數值積分［J］. 計算機學報，2008，21(2):196 -206.ZHOU Yong-quan，ZHANG Ming，ZHAO Bin. Solving numerical integration based on evolution strategy method［J］.Chinese Journal of Computers，2008，21(2):196 -206.

［6］ 王小華，何怡剛，曾喆昭.三角基函數神經網絡算法在數值積分中的運用研究［J］. 電子與信息學報，2004，26(3):394 -399.WANG Xiao-hua，HE Yi-gang，ZENG Zhe-zhao.Numerical integration study based on triangle basis neural network algorithm［J］.Journal of Electronics ＆ Information Technology，2004，26(3):394 -399.

［7］ 曲良東，何登旭，曾邵東.基于人工魚群算法的優化分割數值積分算法［J］.計算機應用與軟件，2009，26(11):58 -60.QU Liang-dong，HE Deng-xu，ZENG Shao-dong.Numerical integration with optim-ized segmentation based on artificial fish-school algorithm［J］. Computer Applications and Software，2009，26(11):58 -60.

［8］ 黃華娟，周永權，韋杏瓊，等.求解矩陣特征值得混合人工魚群算法［J］.計算機工程與應用，2010，46(6):56 -59.HUANG Hua-juan，ZHOU Yong-quan，WEI Xingqiong，et al. Hybrid artificial fish sch-ool algorithm for solving matrix eigenvalues［J］. Computer Engineering and Applications，2010，46(6):56 -59.

［9］ 王冬冬，周永權.人工魚群算法在求解非線性方程組中的應用［J］.計算機應用研究，2007，24(6):242 -244.WANG Dong-dong，ZHOU Yong-quan.. Artificial fishswarm algorithm for solving nonlinear equations［J］.Application Research of Computers，2007，24(6):242 -244.

［10］ 曲良東，何登旭.改進的人工魚群算法及其在近似求導中的應用［J］. 微電子學與計算機，2009，26(5):122 -125.QU Liang-dong，HE Deng-xu. Improved artificial fish school algorithm and its application for solving numerical derivative［J］.Microel Ectronics ＆ Computer，2009，26(5):122 -125.

［11］ Robert C P，Casella G. Monte carlo statistical method(Second Edition)［M］.New York:Springer，2004.

［12］ 徐鐘濟.蒙特卡羅方法［M］. 上海:上海科學技術出版社，1985.XU Zhong-ji. Monte carlo method［M］. Shanghai:Shanghai Science and Technology Press，1985.

［13］ 劉輝玲，葉 鋒.計算多重積分的均勻隨機數蒙特卡羅法的實現［J］.電腦知識與技術，2008，4(8):2 289-2 291.LIU Hui-ling，YE Feng.Realization of monte carlo method by using uniform random sequence for calculating multiple integrals［J］. Computer Knowledge and Technology，2008，4(8):2 289 -2 291.

［14］ 聶黎明，周永權.用人工魚群算法求解二重數值積分［J］.算機工程與應用，2009，45(10):34 -37.NIE Li-ming，ZHOU Yong-quan. Using artificial fishswarm algorithm for solving two dimensional numerical integration［J］.Computer Engineering and Applications，2009，45(10):34 -37.

［15］ 李滿枝，王洪濤，張廣路. 蒙特卡羅法在二重積分中的改進算法［J］. 海南師范大學學報:自然科學版，2010，23(3):242 -244.LI Man-zhi，WANG Hong-tao，ZHANG Guang-lu.Calculation of double integrals based on monte carlo method［J］. Journal of Hainan Normal University:Natural Science，2010，23(3):242 -244.

［16］ 曹承志，張 坤，鄭海英，等. 基于人工魚群算法的BP 神經網絡速度辨識器［J］. 系統仿真學報，2009，21(4):1 047 -1 050.CAO Cheng-zhi，ZHANG Kun，ZHENG Hai-ying，et al.BP neural network speed identifier based on Artificial Fish Algorithm［J］.Journal of System Simulation，2009，21(4):1 047 -1 050.

［17］ 謝竹誠，周永權.一種基于AFSA 與RST 分類規則挖掘算法［J］.微電子學與計算機，2009，26(3):182 -184.XIE Zhu-cheng，ZHOU Yong-quan.Mining classification rules algorithm based on AFSA and RST［J］.Microelectronics ＆ Computer，2009，26(3):182 -184.