一個新數論函數的均值*

董小茹

(西北大學 數學系，陜西 西安710127)

0 引 言

數論，在數學中就是研究數的規律，特別是研究整數性質的數學。它與幾何學一樣，是數學中最古老的分支，在現代基礎數學研究中占有非常重要而又特殊的地位［1-5］。

當自變量n 在某個整數集合中取值，因變量y取實數值或復數值的函數稱之為數論函數，由于很多情形下他們可以看成是特殊的序列，因此數論函數的性質研究在數論中占有舉足輕重的地位，很多重要的算術函數的單個取值是沒有規律的，更不要說給出一個具體的通式顯然是不可能的，但是其均值往往具有非常規則的漸近公式［6-8］。因而數論函數的均值估計問題在數論研究中占有非常重要的位置，是眾多學者研究的課題之一，數論中很多領域都與此有密切的聯系［9-12］，因而在這一領域取得任何實質性的進展都將對數論有很重要的推動作用［13-15］。

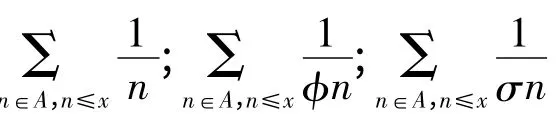
文中的目的是利用初等方法研究了Smarandache 可乘函數J(n)在簡單數中的均值性質，并給出了一個有趣的漸近式。其中用到了以下內容:歐拉函數，即對任意正整數n ≥1，Euler 函數φ(n)表示為所有不超過n 且與n 互素的正整數的個數。

類似的，也定義函數J(n)為模n 所有原Dirichlet 特征的個數，即J(n)= n(p -1)2.具體的證明應用Abel 恒等式，級數的收斂性等知識。

1 引理的證明

引理1 若n 為簡單數，則n 的取值只能為n= p，n = p2，n = p3，n = pq 這4 種情況，其中p，q 是不同的素數。

證明 參見文獻［3］

引理2

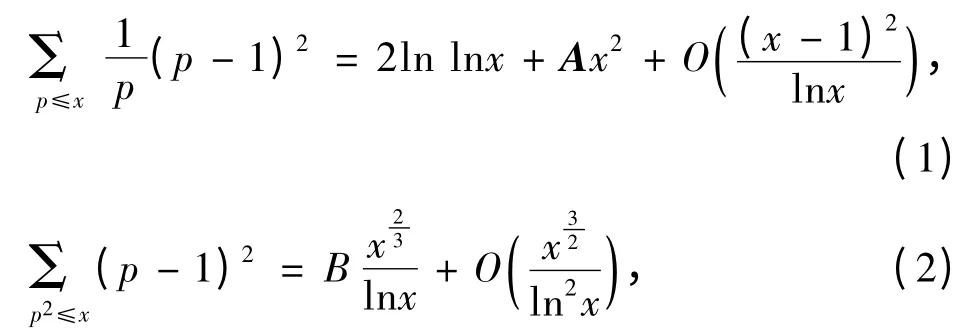
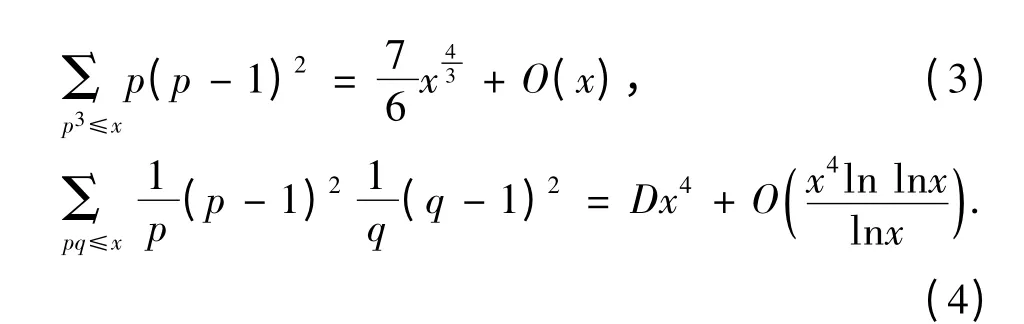
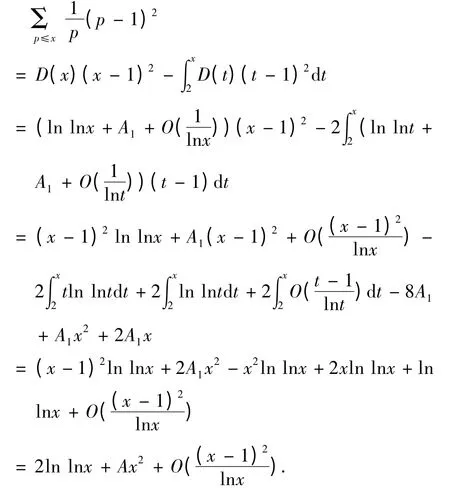
同理可證

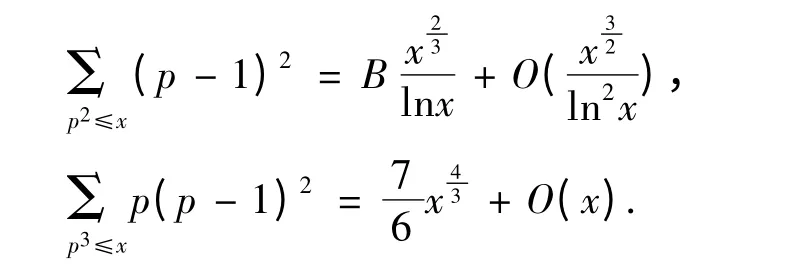
其中用到

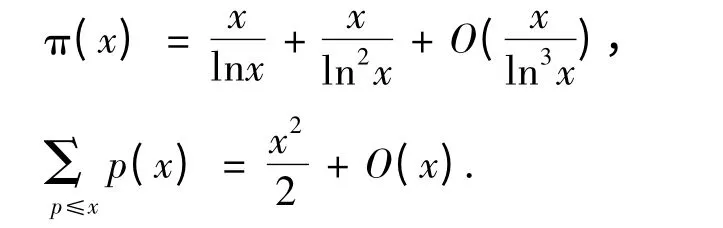
下面證明(4)，應用拆分原理。

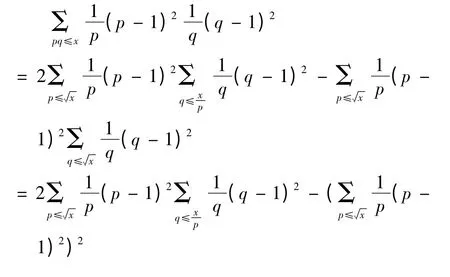
而

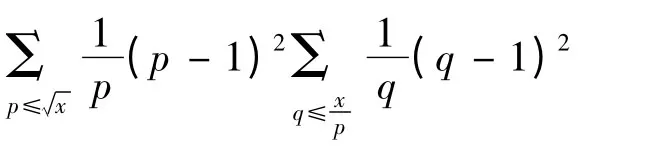
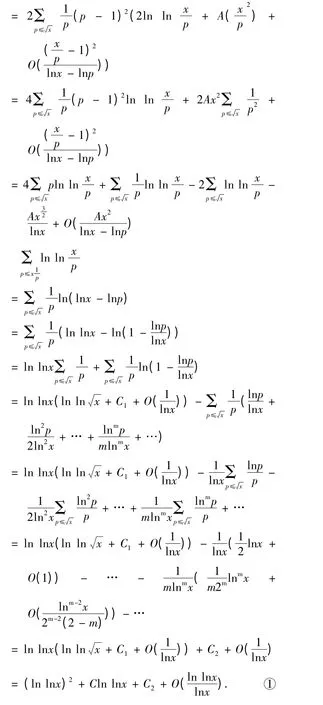
其中用到

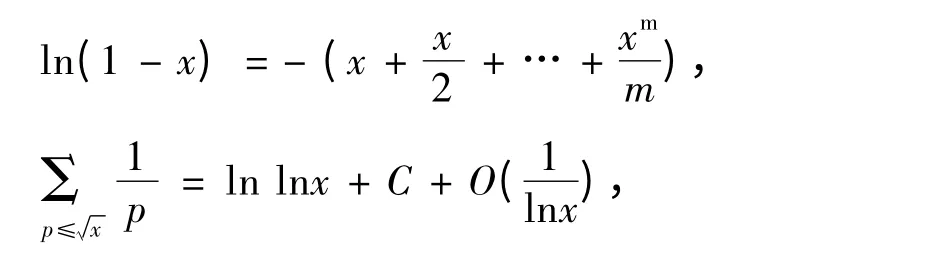
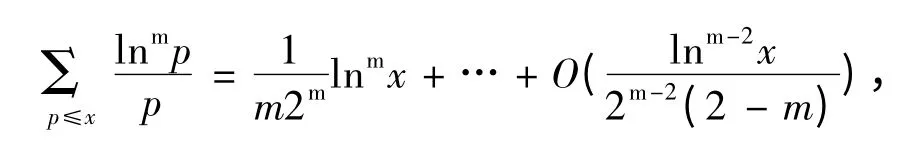
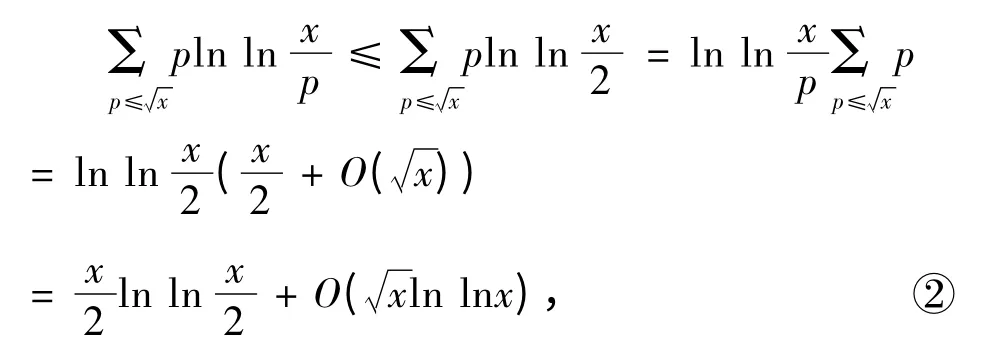
同理

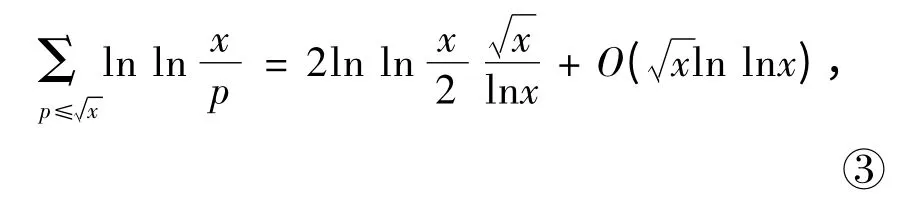
所以由①②③式有

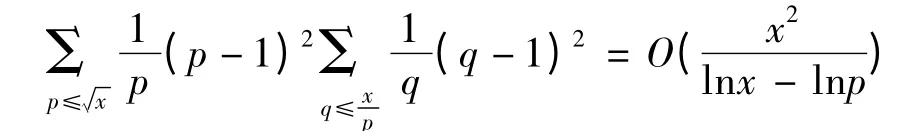
而(4)式變為

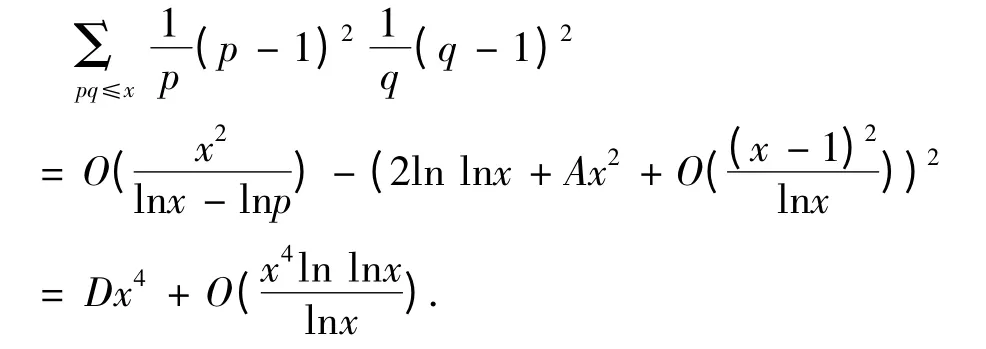
于是完成了引理2 的證明。

2 定理的證明

現在給出定理的證明。事實上，根據引理1 及引理2 可以得到

對任意對任意x ∈R，x ≥3，有漸近式

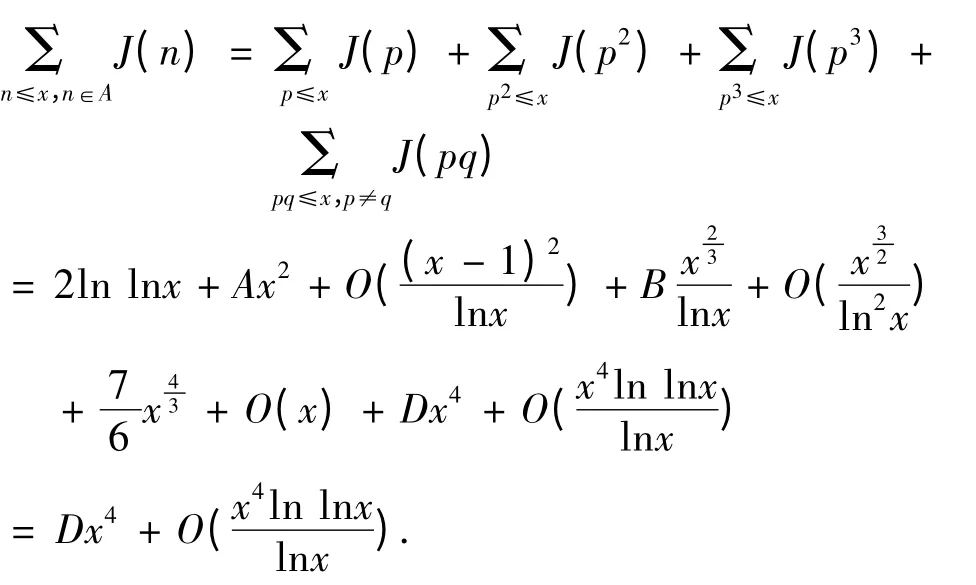
綜上所述，定理證畢。

References

［1］ Smarandache F. Only problems，not solutions［M］. Chicago:Xiquan Press，1993.

［2］ 張文鵬.初等數論［M］.西安:陜西師范大學，2007.ZHANG Wen-peng.Elementary number theory［M］.Xi’an:Shaanxi Normal University Press，2007.

［3］ Liu H Y. On the simple numbers and the mean value properties［J］. Smarandache Notions Journal，2002(14):171 -175.

［4］ 蘇娟麗.關于Smarandache 因子個數為n 的最小數問題［J］.西安工程大學學報，2012，26(4):532 -535.SU Juan-li.On the smarandache smallest number with n divisors sequence［J］. Journal of Xi’an Polytechnic University，2012，26(4):532 -535.

［5］ 王明軍.關于簡單數序列的一些研究［J］. 西南師范大學學報:自然科學版，2011，36(3):14 -16.WANG Ming-jun.Some studies on the sequence of simple number［J］.Journal of Southwest China Normal University:Natural Science Edition，2011，36(3):14 -16.

［6］ 王明軍.關于一個可乘函數及其均值［J］. 北華大學學報:自然科學版，2012，13(4):395 -397.WANG Ming-jun. On a multiplicative function and its mean value［J］. Journal of Beihua University:Natural Science Edition，2012，13(4):395 -397.

［7］ 張小蹦.關于Smarandache 可乘函數的均值研究［J］.西安郵電學院學報，2008，13(1):139 -140.ZHANG Xiao-beng. Mean value of smarandache multiplicative function［J］. Journal of Xi’an University of Post and Telecommunications，2008，13(1):139 -140.

［8］ 張 拓.關于課程函數的復合函數均值［J］. 科學技術與工程，2010，10(28):6 954 -6 956.ZHANG Tuo. One hybrid mean value formula of multiplicative function［J］.Science Technology and Engineering，2010，10(28):6 954 -6 956.

［9］ 高 麗，謝 瑞，趙 秦. 兩個包含近似偽Smarandache 函數的漸近公式［J］.延安大學學報:自然科學版，2011，30(2):1 -3.GAO Li，XIE Rui，ZHAO Qin. Two arithmetical functions involving near pseudo smarandache notions and their asymptotic forulas［J］. Journal of Yanan University:Natural Science Edition，2011，30(2):1 -3.

［10］藺小林，李仲博，劉 侃.多項交錯級數斂散性的判定方法［J］.陜西科技大學學報，2013，31(2):150 -154.LIN Xiao-lin，LI Zhong-bo，LIU Kan.On the converence criteria for multi-alternating series［J］. Journal of Shaanxi University of Science＆ Technology，2013，31(2):150 -154.

［11］朱遠暉，樊 琦.雙參數拋物型Mohr 強度準則研究［J］.西安科技大學學報，2013，33(2):244 -248.ZHU Yuan-hui，FAN Qi. Research on two-parameter parabolic Mohr strength criterion［J］. Journal of Xi’an University of Science ＆ Technology，2013，33(2):244-248.

［12］楊宏才.打緯曲軸系統的臨界轉速計算與分析［J］.西安科技大學學報，2013，33(1):117 -121.YANG Hong-cai.Calculation and analysis of crankshaft’s critical speed［J］.Journal of Xi’an University of Science ＆ Technology，2013，33(1):117 -121.

［13］趙高長.模擬故障數據的構造算法研究［J］. 西安科技大學學報，2011，31(2):230 -235.ZHAO Gao-chang. Algorithms for simulating fault data［J］.Journal of Xi’an University of Science ＆ Technology，2011，31(2):230 -235.

［14］李明明.用于環境監測領域無線傳感器網絡中的數據壓縮編碼算法［J］. 西安科技大學學報，2011，31(5):617 -620.LI Ming-ming.A data compression algorithm for environmentmonitoring wireless sensor network［J］. Journal of Xi’an University of Science ＆ Technology，2011，31(5):617 -620.

［15］張曉莉，遲敏娜，李白萍. TD-SCDMA 基于信號強度和質量的切換算法［J］.西安科技大學學報，2011，31(3):376 -379.ZHANG Xiao-li，CHI Min-na，LI Bai-ping. Investigation of handover algorithm based on combining of signal strength and quality of TD-SCDMA［J］. Journal of Xi’an University of Science ＆ Technology，2011，31(3):376 -379.