灰色關聯分析在產業發展研究中的應用——以天津軟件產業為例

◎文/郄紅偉 趙 珵 朱司宇

一、產業發展研究的一般視角

產業是經濟的主體和支撐，產業發展是經濟發展的內容，開展產業發展研究對于實現經濟的又好又快發展具有重要意義。

產業研究的內容包含四個方面：一是產業內部各企業之間相互作用關系的規律，二是產業本身的發展規律，三是產業與產業之間互動聯系的規律，四是產業在空間區域中的分布規律等。四個方面的研究旨在激發積極因素，遏制不利因素，最終推動產業的發展。作為政府層面的產業發展研究，更多的集中于研究產業發展規律，分析影響產業發展的內部和外部因素，促進產業資源優化布局和最大化利用。

產業發展是指產業的產生、成長和進化過程，既包括單個產業的進化過程，又包括產業總體，即整個國民經濟的進化過程。而進化過程既包括某一產業中企業數量、產品或者服務產量等數量上的變化，也包括產業結構的調整、變化、更替和產業主導位置等質量上的變化，而且主要以結構變化為核心，以產業結構優化為發展方向。因此，產業發展包括量的增加和質的飛躍，包括絕對的增長和相對的增長。

當前產業發展研究的方法一是基于資料的定性分析，二是基于各類數據的簡單統計分析，三是利用各種科學計量方法分析產業發展影響因素和發展規律，預測產業未來發展規模。本論文主要討論灰色關聯分析方法在產業發展影響因素分析中的應用。

二、灰色關聯分析基本概述

（一）灰色系統與灰色關聯分析

灰色系統理論是20世紀80年代，由中國華中理工大學鄧聚龍教授首先提出并創立的一門新興學科，它是基于數學理論的系統工程學科。灰色系統理論以“部分信息已知，部分信息未知”的“小樣本”、“貧信息”不確定性系統為研究對象，主要通過對“部分”已知信息的生成、開發，提取有價值的信息，實現對系統運行行為、演化規律的正確描述和有效監控。

灰色關聯分析是灰色系統理論的重要組成部分之一，是通過灰色關聯度來分析和確定系統中各因素之間的影響程度或因素對系統主行為的貢獻程度的一種方法。關聯度是事物之間、因素之間關聯性的“度量”，它通過從隨機性的序列中找到關聯性，從而為因素分析、預測的精度分析提供依據，為決策提供基礎。

（二）灰色關聯分析與統計分析方法的區別

數理統計中的回歸分析、方差分析、主成分分析等都是用來進行系統分析的方法，但這些方法要求必須具備大量數據，如果數據量少就難以找出統計規律；要求各因素數據與系統特征數據之間呈線性關系并且彼此無關；要求樣本數據服從某個典型的概率分布。但是在實際工作中，這種要求往往難以滿足，尤其是在我國統計數據比較有限，而且現有數據灰度較大的情況下，許多數據難以找到典型的分布規律。往往計算量大、過程復雜，常需要借助計算軟件，可能出現量化結果與定性分析結果不符的現象，導致系統的關系和規律遭到歪曲和顛倒。

灰色關聯分析從某種程度上彌補了上述缺憾，它對樣本量的多少和樣本有無規律都同樣適用，而且計算量小，分析的結果一般與定性分析相吻合。因此，灰色關聯分析是系統分析中很有獨特優勢、比較實用和可到的分析方法。

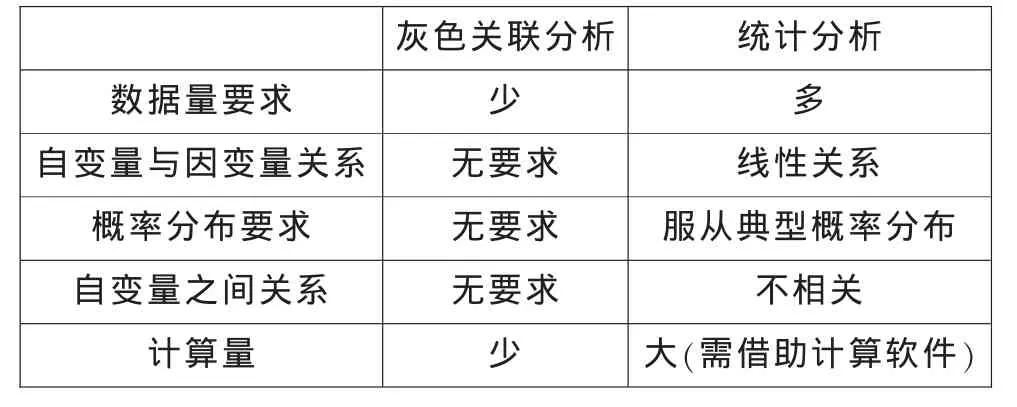
表1 灰色關聯分析與統計分析方法的區別

（三）灰色關聯分析的應用流程和方法

進行灰色關聯分析從大的方面一般需要四個流程：一是建立指標體系，二是生成灰色序列，三是計算灰色關聯度，四是基于計算結果并結合實際情況對結果進行分析，提出對策。

1.建立指標體系

指標體系的建立是為了更好地測度哪些因素對產業發展影響較大，為相關決策提供現實量化的依據，指標的選擇主要基于以下原則：

客觀性原則。指標體系的建立應結合產業實際和經濟發展水平，并且體系建立之后的實證研究也必須遵循這一原則，在搜集數據的過程中盡量采用原始數據，數據源應權威可靠。

可操作性原則。設計的指標數據應容易獲得，進而能夠科學地應用于評價實際，發揮其應有的評價功能。同時指標應具有比較性和可測性，計算方法容易掌握，這樣才能有其現實的意義。

系統性原則。指標體系的建立要處理好部分與整體、具體行動與系統目標之間的關系。作為一個有機整體不但應從各個層次、各個角度反映被評價對象的特征和狀況，而且還要體現對象的變化趨勢，反映對象的發展動態。

代表性原則。由于影響產業發展的因素很多，作為系統化的指標體系，要在眾多可用指標中篩選最具代表性、最靈敏的主導性指標。

2.生成灰色序列

對一個抽象的系統或現象進行分析，首先要選準反映系統行為特征的數據序列。例如，用國民平均接受教育的年數來反映教育發達程度，用刑事案件的發案率來反映社會治安面貌和社會秩序，用醫院掛號次數來反映國民的健康水平等。有了系統行為特征數據和相關因素的數據，即可做出各個序列的圖形，從直觀上進行分析。

因為灰色關聯分析是通過對少量的原始數據進行分析來尋求規律，而這少量的原始數據具有一定的隨機性。因此，應該通過某種生成方法來弱化其隨機性，顯示其規律性。緩沖算子是對原始數據進行處理的一種方法，緩沖算子包括兩類，一是弱化緩沖算子，二是強化緩沖算子。

（1）弱化緩沖算子。設為系統行為數據系列，為緩沖算子，當分別為單調增長序列，單調衰減序列或者震蕩序列時，緩沖序列比行為序列的增長速度（或衰減速度）減緩或振幅減小，稱緩沖算子為弱化緩沖算子。

生成灰色序列需要結合對原始數據的分析以及環境的考慮，如果原始數據增長或衰減較快，明顯高于正常增速（減速），則需要弱化序列的增長（衰減）趨勢。如，產業發展之初由于基數較小，加之政策的扶持，增速較快；但是隨著產業的日漸成熟，規模的擴大，相應的扶持政策也將弱化，在大的基數上實現較快增長也很困難，因此增速勢必會下降。

當前較為廣泛使用的弱化緩沖算子計算方法主要有：平均弱化緩沖算子、幾何平均弱化緩沖算子、加權平均弱化緩沖算子、加權幾何平均弱化緩沖算子。一些學者在此基礎上對弱化緩沖算子進行了擴展研究。各種弱化緩沖算子均有一定的計算模型，可參考文獻[1]，在此不再贅述。

如果要降低弱化速度，可以使用加權幾何平均弱化緩沖算子；如果要提高弱化速度，可以使用加權平均弱化緩沖算子；在同一類算子中，可通過變化不同時期數據的權重適當調整弱化速度。

（2）強化緩沖算子。設為系統行為數據系列，為緩沖算子，當分別為單調增長序列，單調衰減序列或者震蕩序列時，緩沖序列比行為序列的增長速度（或衰減速度）加快或振幅增大，稱緩沖算子為強化緩沖算子。

如果原始數據增長（衰減）較慢，明顯低于正常增速（減速），則需要強化序列的增長（衰減）趨勢。如，受金融危機的影響，從2008年開始，很多產業增速甚至規模出現下滑，如果以這一時段的數據尋求產業發展規律，勢必會出現偏頗。因此，應強化原始數據的增長趨勢。

當前較為廣泛使用的強化緩沖算子計算方法主要有：平均強化緩沖算子、幾何平均強化緩沖算子、加權平均強化緩沖算子、加權幾何平均強化緩沖算子。一些學者在此基礎上對強化緩沖算子進行了擴展研究。各種強化緩沖算子均有一定的計算模型，可參考文獻[2]，在此不再贅述。

如果要使強化速度快一些，可使用加權幾何平均強化算子；如果想使強化速度慢一些，可使用加權平均強化緩沖算子；在同一類算子中，還可以通過調整各時期數據的權重改變強化速度。

當然，如果數據未出現增長（衰減）較快（較慢）的情況，能夠代表產業發展趨勢，可以不利用上述方法生成序列。此外，在搜集數據時，常常由于一些不易克服的困難導致數據序列出現空缺，也有些數據序列雖然完整，但由于系統行為在某個時點上發生突變而形成異常數據，這時如果剔除異常數據就會留下空穴，面對這種情況可以利用均值生成算子。

3.計算灰色關聯度

如果各因素具有不同的量綱，計算灰色關聯度之前應首先對序列數據進行無量綱化處理，使得數據能夠橫向對比。當前無量綱化處理的方法主要有初值化生成、均值化生成、區間生成、逆化生成和倒數化生成。

從現有的研究來看，判斷因素數據序列間關聯度的方法主要有：鄧氏關聯度、絕對關聯度、相對關聯度、斜率關聯度、T型關聯度、C型關聯度、改進的關聯度等典型方法，此外，還有眾多學者對上述計算方法進行了改進，形成許多新的改進模型。這些方法大致可以分為三類：一類是強調序列的絕對位置差，如鄧氏關聯度、灰色絕對關聯度、T型關聯度等；一類是強調序列的變化率，如B型關聯度、斜率關聯度等；此外，還有一些關聯度的構造建立在上述兩角度的基礎之上，即考慮絕對變化，又考慮相對變化。

關聯度計算方法的選擇應基于以下三個原則：（1）優先選取即涵蓋絕對位置差又涵蓋變化率的灰色關聯度算法模型，這也是一種未來研究的趨勢。（2）優先考慮保序性，保序性即無論是否進行無量綱化處理以及采用何種無量綱化處理方法（初值化、均值化、標準化等）均不會影響各因素的關聯度大小。（3）結合定性分析，在應用灰色關聯分析方法之前，一定要進行相應的定性分析，確認所研究的問題滿足或適合灰關聯分析的應用前提和條件。否則，研究結論的可靠性會遭到懷疑。

4.計算結果分析

利用上面的各個模型計算出來的灰色關聯度的大小是衡量序列之間緊密程度的一種尺度，而在進行系統分析時，研究系統特征行為與因素行為之間的關系，應關注的重點是系統特征行為序列和各個因素行為序列關聯度大小的順序，而不完全是關注度在數值上的大小。同時也要結合產業的發展實際以及內外部環境對評價結果進行驗證，在關聯度排序靠前的因素對系統特征行為的影響較大，反之較小。最后要根據各因素影響力的大小提出相應的對策建議。

三、灰色關聯分析在天津軟件產業發展研究中的應用

（一）天津軟件產業發展灰色關聯分析

1.指標選取

基于指標體系建立原則，本文選取了軟件業務收入X1、納入統計的軟件企業數Y1（代表企業規模）、軟件業務收入過億元企業Y2（代表企業質量）、登記軟件產品數量Y3（代表產品質量）、軟件從業人員Y4（代表人員規模）、研發經費投入Y5（代表創新投入）、嵌入式軟件所占比重Y6（代表產業結構）。以軟件業務收入為母因素，其余指標為子因素，分析各子因素對軟件業務收入的影響。

2.生成灰色序列

計算原始數據的增長速度（見表2）。由表可見，納入統計的軟件企業數在2009年、2011年和2012年有一定的突變，軟件業務收入過億元企業在2009年出現突變，因此，采用緊鄰均值生成序列；研發經費變化不定，增長和降低速度均較快，因此，采用平均弱化緩沖算子進行計算。計算結果見表3。

3.計算灰色關聯度

（1）無量綱化處理。因為選取的指標量綱不同，為便于比較，對表3中的數據進行無量綱化處理，本文選取均值化生成（見表4）。

（2）計算灰色關聯度。本部分利用孫玉剛在《灰色關聯分析及其應用的研究》中改進的灰色斜率關聯度算法進行計算，因為該算法具有規范性、保序性、對稱性、唯一性、可比性，并且能夠體現關聯度的正負性問題。計算公式為：

表2 原始數據的同比增長率

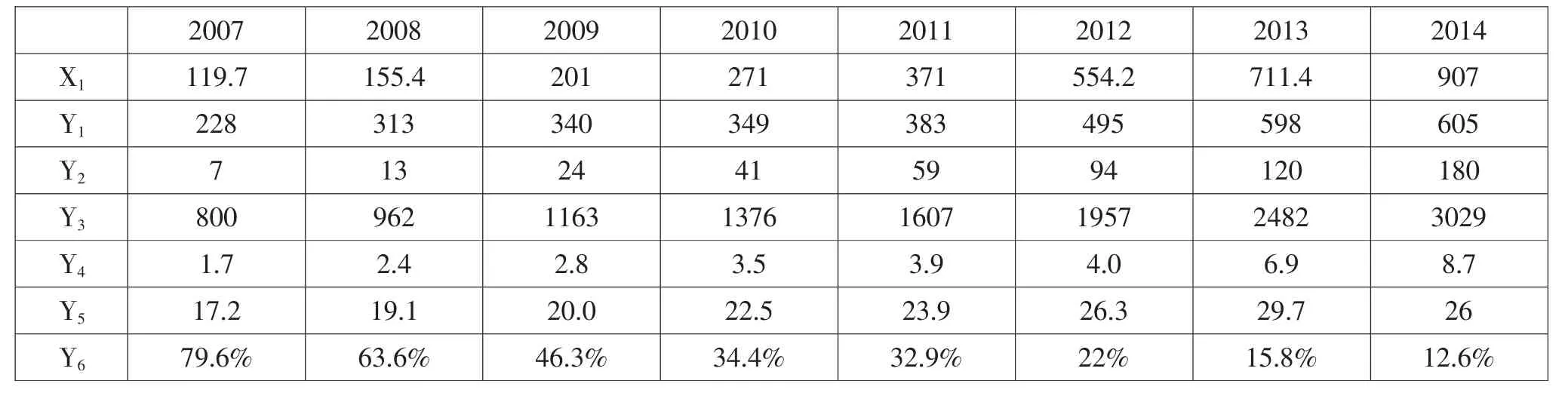
表3 均值生成后的序列算子

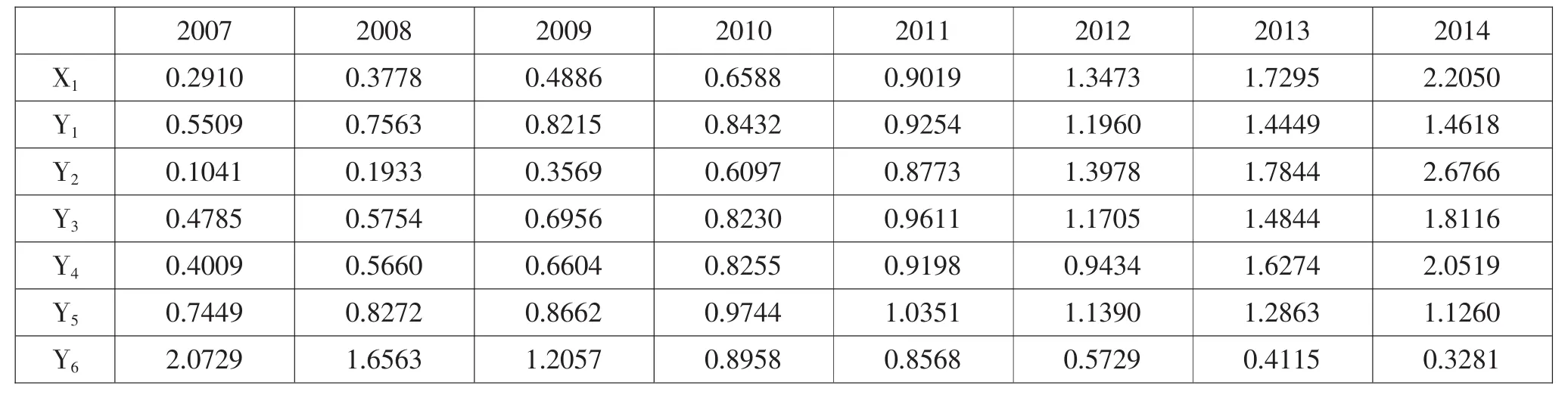
表4 無量鋼化后的序列算子

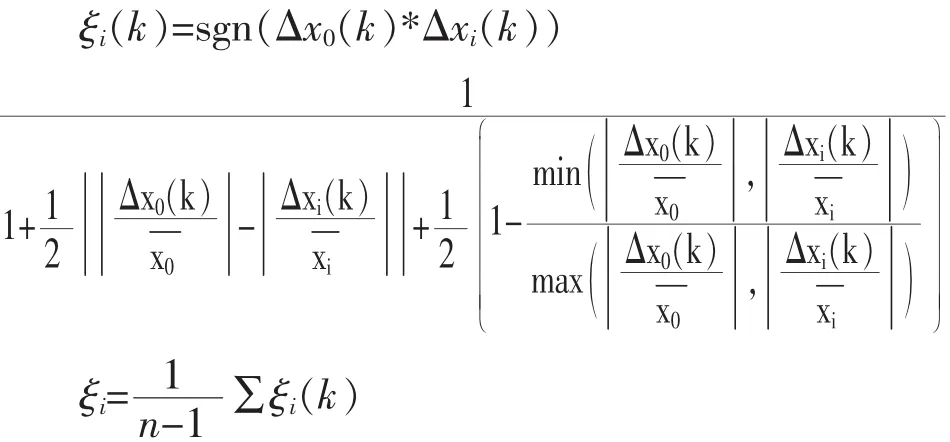
根據上述公式進行計算得到各因素與軟件業務收入的關聯度，見表5。

表5 灰色關聯度計算結果

對計算結果進行排序，即軟件業務收入過億元企業的數量對產業發展的影響最大，其次是軟件從業人員，之后是研發經費投入、登記軟件產品數量、納入統計的軟件企業數量，而嵌入式軟件所占的比重與產業發展負相關。

（二）天津軟件產業發展對策

根據上述計算結果可以提出如下發展對策。

1.著力發展壯大規模型軟件企業

規模型企業尤其是龍頭企業對于產業發展的貢獻度較大，一方面應瞄準全球軟件五百強和中國軟件百強企業，加大招商引資力度；另一方面，應加大對本土軟件企業的扶持力度，通過項目扶持、政府采購等方式，鼓勵企業做大做強；此外，還要鼓勵企業合并、重組，充分集成多方優勢，培育企業實力、壯大企業規模。

2.著力壯大軟件人才隊伍

多年來，軟件人才總量不足、高端軟件人才缺乏一直是制約天津軟件產業發展的一個瓶頸，由于毗鄰北京加之工資水平較低，很多軟件人才都流失到北京、上海等城市。

今后應發揮好天津市大學軟件園的作用，加大軟件人才培養力度；要加強對現有軟件人才的培訓力度；要借助近幾年天津經濟發展較快，而消費相對較低的比較優勢，留住現有人才，同時吸引一批高端人才。

3.鼓勵企業加大研發投入

從全國范圍來看，我國軟件產業起步較晚，大部分軟件產品被外國壟斷，軟件服務外包長期以來在產業中占有很大比重，因此企業普遍對研發經費的投入不重視。而要真正能夠培育出具有市場競爭力的軟件產品，打破國外的壟斷，必需發揮企業的主體作用，加強產學研聯合攻關，建立多元化投入體系，加大研發投入。

4.著力培育一批具有競爭力的軟件產品

軟件產品在軟件業務收入中所占的比重是衡量產業結構的一重要指標，而同時，一個具有競爭力的軟件產品能夠帶動企業快速占領市場，帶動產業規模迅速擴大。近幾年天津的這一比重雖有提高，但總體還較低。因此，應加大扶持力度，鼓勵企業開發或產學研聯合開發一批具有競爭力的軟件產品。

5.做大軟件企業的群體規模

要把握當前科技型中小企業蓬勃發展的戰略機遇，加大政策宣傳力度，鼓勵各類科技人員創辦領班軟件企業；同時鼓勵其他行業內設的信息部門、軟件部門獨立，成立獨立的軟件公司，享受國務院關于進一步鼓勵軟件和集成電路產業發展的相關政策。通過企業群體規模的擴大，帶動產業規模的擴大。

6.進一步縮小嵌入式軟件比重

嵌入式軟件所占的比重與軟件產業發展負相關，主要是由于我國對嵌入式軟件的統計采用制造業收入乘以一定的比重，嵌入式軟件一直是低端的代表。近年來，天津不斷加大軟件產業結構的調整，嵌入式軟件所占的比重逐年下降，但是仍高于全國平均水平，還應進一步加大調整力度。

[1]黨耀國，劉思峰，劉斌，唐學文.關于弱化緩沖算子的研究[J].中國管理科學，2004（2）:108-111.

[2]黨耀國，劉斌，關葉青.關于強化緩沖算子的研究[J].控制與決策，2005（12）:1332-1336.

[3]黨耀國，劉思峰，王正新，林益.灰色預測與決策模型研究[M].北京：科學出版社，2009:64-65.

[4]田民 ，劉思峰，卜志坤.灰色關聯度算法模型的研究綜述[J].統計與決策，2008（1）：24-27.

[5]孫玉剛.灰色關聯分析及其應用的研究[D].南京：南京航空航天大學碩士論文，2007.

[6]曹明霞.灰色關聯分析模型及其應用的研究[D].南京：南京航空航天大學碩士論文，2007.