光伏發電跟蹤支架陰影數學模型研究

特變電工新疆新能源股份有限公司 ■ 何銀濤 張梅 黃華

0 引言

陰影遮擋是影響光伏發電的主要因素之一，因此，GB 50797-2012《光伏發電站設計規范》要求[1]，光伏方陣間距設置要保證在全年每天9:00～15:00(當地真太陽時)時段內相鄰支架不互相遮擋。光伏發電跟蹤支架相比于固定式支架，發電量有明顯提高[2]，但其陰影變化情況更加復雜。目前，針對跟蹤支架的控制系統精度和效率方面的研究較多[3,4]，對于跟蹤支架運行過程中陰影的變化研究較少，而這一研究對于科學合理地設置相鄰跟蹤支架排布間距有重要意義。

本文根據特變電工哈密863實驗電站中3種常用跟蹤支架的運動規律，建立跟蹤支架陰影數學模型，從而為科學合理地確定相鄰跟蹤支架排布間距、高效利用土地資源提供理論依據。

1 建立跟蹤支架數學模型

根據跟蹤支架運動規律，建立適當的坐標系，并分別給出組串平面4個角點在運動范圍內的軌跡方程，進而得到跟蹤支架位置的數學模型。

1.1 平單軸跟蹤支架

圖1為平單軸跟蹤支架的俯視圖和左視圖。建立如圖1b所示坐標系o-xyz，其中，z軸垂直于xoy平面。平單軸跟蹤支架轉動軸與水平面平行，南北向布置，東西向轉動，ox指向正西方向，oz指向正北方向；A1-D1和A2-D2為AD轉動范圍內的兩個任意位置，θ為跟蹤轉角；o點離地面的距離為H，L為組串長度，2R為組串寬度。

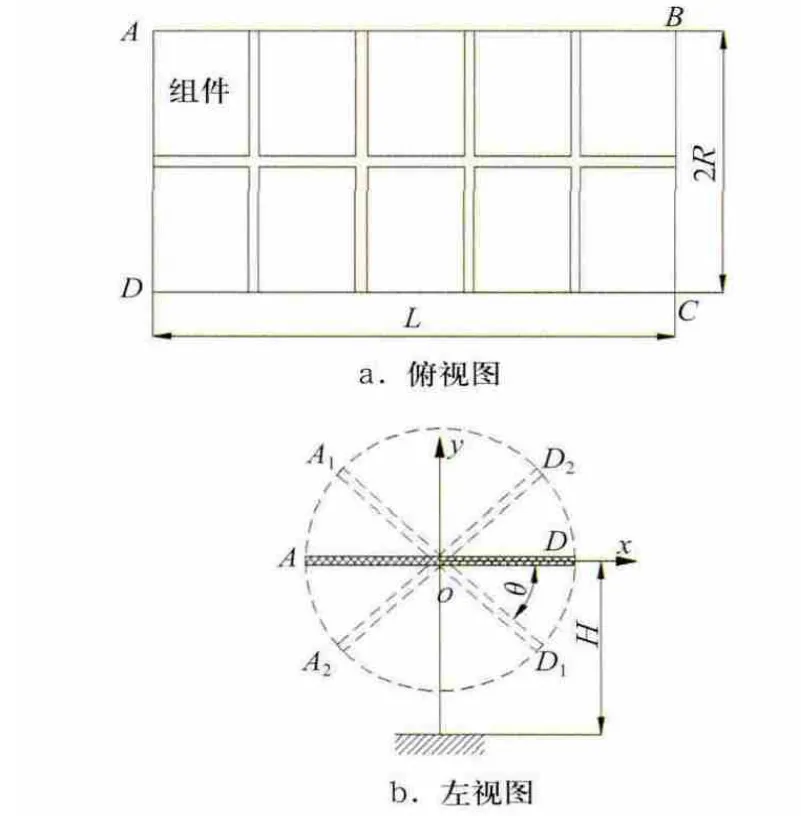
圖1 平單軸跟蹤支架結構簡圖

根據平單軸轉動規律，D點軌跡可表示為：

A、B、C 3點的坐標和D點關系式為：

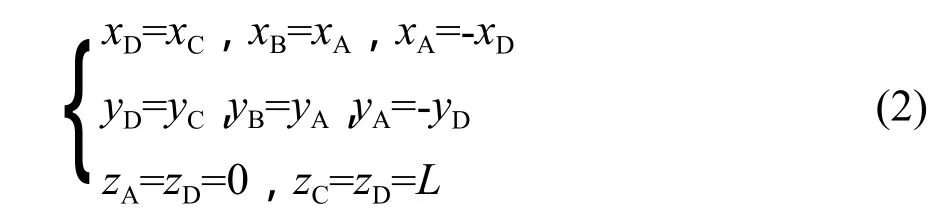
根據以上關系式可求得A、B、C、D 4點在坐標系o-xyz中的坐標，即得到平單軸位置數學模型。

1.2 斜單軸跟蹤支架

圖2 斜單軸跟蹤支架結構簡圖

圖2為斜單軸跟蹤支架的前視圖，組串平面與水平面垂直。建立如圖2所示坐標系o-x1y1z1，x1軸垂直于y1oz1平面。斜單軸跟蹤支架轉動軸與水平面夾角α，且轉動軸南北向布置，東西向轉動；oz1沿轉動軸方向，oy1軸沿AD邊指向上方；轉動軸低端離地面的距離為H1，高端離地面高度為H2；L為組串長度，2R為組串寬度。

根據布爾莎-沃爾夫轉換模型[5]，對坐標系o-x1y1z1進行一次坐標變換，即繞y1軸逆時針旋轉角度α，得到坐標系o-xyz，變換關系用矩陣形式表示為：

變換后得到的坐標系o-xyz與圖1b中平單軸的坐標系一致。則在坐標系o-xyz中，D點軌跡表示為：

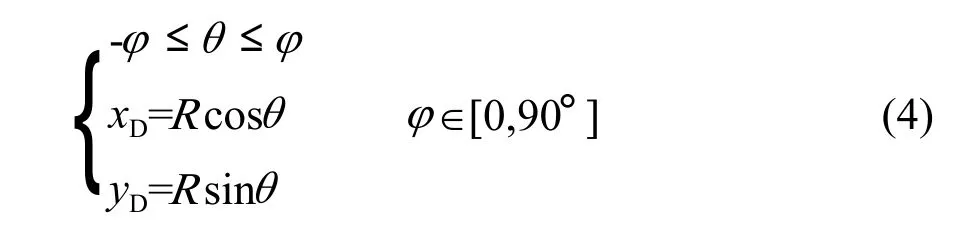
A、B、C 3點的坐標和D點關系式為：

再根據式(3)變換關系就可求得A、B、C、D在坐標系o-x1y1z1中坐標(xli, yli, zli)，其中i=A、B、C、D，即得到斜單軸位置數學模型。

1.3 雙軸跟蹤支架

圖3為雙軸跟蹤支架的結構簡圖，組串平面ABCD為矩形。建立如圖3所示坐標系o-xyz，ox指向正東方向，oz指向正南方向；o點離地面的距離為H；L1為BC長度，L2為AB長度；雙軸跟蹤支架在跟蹤時間范圍內，組串表面時刻與太陽光線垂直。

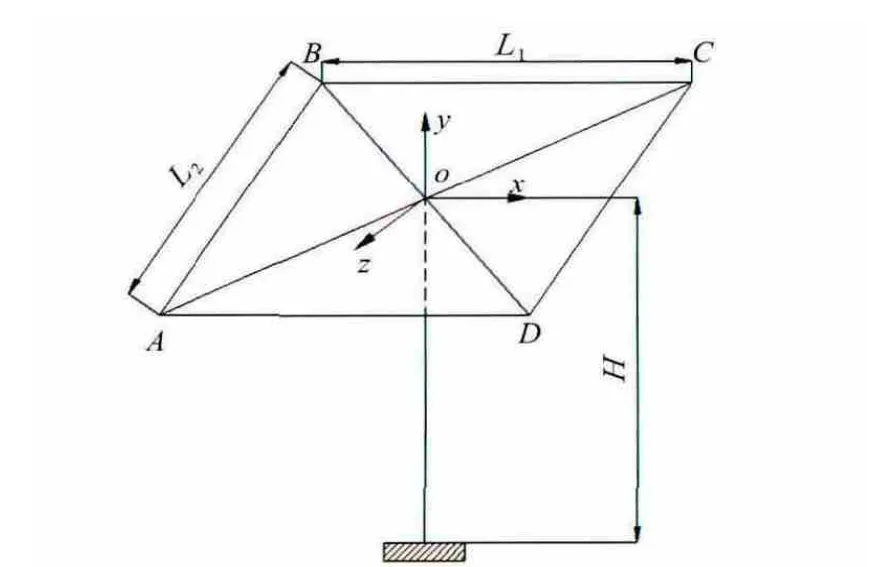
圖3 雙軸跟蹤支架結構簡圖

雙軸支架繞y軸轉動跟蹤太陽方位角，繞x軸轉動跟蹤太陽高度角，組串平面ABCD初始位置在xoz平面內，BC平行于x軸，AB平行于z軸。設在跟蹤過程中，轉動一個位置便建立新的坐標系o-xiyizi，且BC平行于xi軸，AB平行于zi軸，則o-xiyizi可通過坐標系o-xyz坐標變換獲得。在坐標系o-xiyizi中，A、B、C、D坐標表示為：

設某一時刻太陽高度角h，太陽方位角β，則雙軸轉動過程可表示為：先繞y軸轉動γ，再繞x軸轉動，β=90°-h。故根據布爾莎－沃爾夫轉換模型[5]，坐標變換關系表示為：

2 陰影數學模型

遮擋物高度與其陰影長度的幾何關系表示如圖4所示(以A點為例，點A′為A點在地面的影子)。

圖4 遮擋物高度與其陰影長度的幾何關系圖

2.1 平單軸跟蹤支架

根據圖1b和圖4幾何關系，遮擋物高度表示為：HGi=yi+H，則陰影長度Li=HGicoth，陰影長度南北向分量LNSi=|Licosγ|，陰影長度東西向分量LEWi=|Licosγ|，其中，i=A、B、C、D。則A、B、C、D4 點在地面的影子 A′、B′、C′、D′的坐標表達式為：

式中，i=A、B、C、D。

2.2 斜單軸跟蹤支架

參照圖4幾何關系，遮擋物高度表示為：HGk=y1k+H1，k=A、D；HGj=y1j+H2，j=B、C。陰影長度Li=HGicoth，陰影長度南北向分量LNSi=|Licosγ|，陰影長度東西向分量LEWi=|Lisinγ|，其中，i=A、B、C、D。則A、B、C、D 4點在地面的陰影 A′、B′、C′、D′的坐標表達式為：

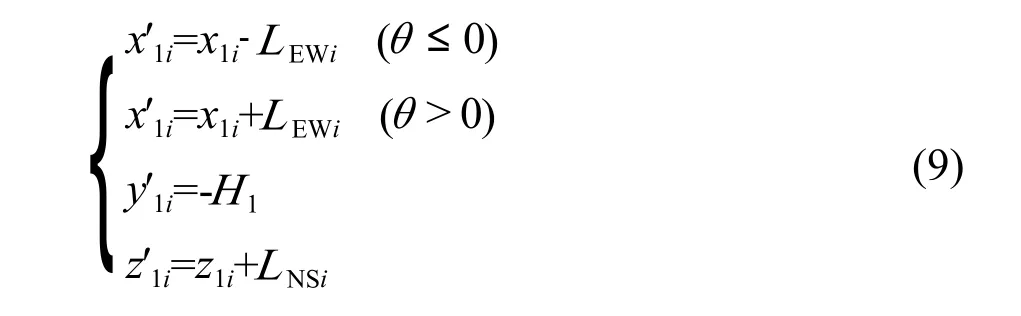
式中，i=A、B、C、D。

2.3 雙軸跟蹤支架

參照圖4幾何關系，遮擋物高度表示為：HGi=yi+H，陰影長度Li=HGicoth，陰影長度南北向分量LNSi=|Licosγ|，陰影長度東西向分量LEWi=|Lisinγ|，其中，i=A、B、C、D。則A、B、C、D 4 點在地面的陰影 A′、B′、C′、D′的坐標表達式為：

式中，i=A、B、C、D

3 計算示例

以陰影變化情況最為復雜的斜單軸為例，對光伏發電跟蹤支架陰影數學模型的計算過程進行說明。

如圖2所示，已知L=10.1 m，R=1.8 m，H1=1.3 m，H2=3.9 m，α=15°；方位角跟蹤范圍為-45°≤θ≤45°；建設地為哈密地區，緯度 42.6°，經度94.9°；并假設地面平整。

冬至日真太陽時9:00，斜單軸跟蹤角度θ=-45°，根據1.2節內容及式(3)可得D點在坐標系o-x1y1z1中坐標為：

同理可得：

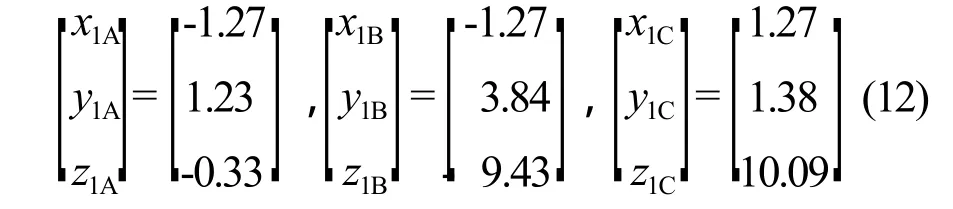
根據太陽角計算公式[6]，建設地(緯度42.6°，經度94.9°)冬至日真太陽時9:00，太陽高度角h=12°，方位角γ=41.56°，再根據2.2節內容，可得：

HGA=1.23+1.3=2.53 m，LA=2.53 cot12°=11.9 m，LNSA=|11.9cos41.56°|=8.9 m，LEWA=|11.9sin41.56°|=7.9 m。則根據式(9)，A點在地面陰影A′ 坐標為：

同理可得：

通過以上計算過程，可得到斜單軸組串在冬至日真太陽時早9:00的姿態(式(11)和式(12))和對應的陰影情況(式(13)和式(14))。

圖5 斜單軸跟蹤支架排布及陰影俯視圖

相鄰斜單軸組串的陰影形狀相同，只要保證相鄰斜單軸組串在地面陰影不重疊，便不會產生遮擋現象，故由幾何關系可得鄰近4個斜單軸組串排布狀況及陰影狀況如圖5所示。藍色框表示斜單軸組串的俯視圖，黑色框表示對應的陰影；設置的東西向間距為7 m，南北向間距18.5 m。

以上是斜單軸的計算示例。平單軸、雙軸計算過程與之類似。

4 結束語

本文建立了3種常用光伏跟蹤支架的陰影數學模型，并以斜單軸跟蹤支架的陰影數學模型為例，對此陰影數學模型的計算過程進行說明，得到了斜單軸在冬至日真太陽時早9:00的位置坐標和陰影坐標；最后，根據幾何關系，得到了合理的斜單軸方陣布置間距，保證整個跟蹤范圍內既不產生相互遮擋現象，又能充分利用土地。

因此，此陰影數學模型對設置光伏跟蹤支架排布的合理間距、優化跟蹤支架方陣占地面積有重要的指導意義。

[1] 中國電力企業聯合會. GB 50797-2012光伏發電站設計規范[M]. 北京: 中國計劃出版社, 2012.

[2] 張峰, 王垚, 陳正安, 等. 光伏電站跟蹤系統的技術分析和比較[A]. 中國電機工程學會清潔高效燃煤發電技術協作網2009年會論文集[C], 2009, 1－6.

[3] 張相明, 鄧瑋, 關煥新, 等. 光伏發電雙軸自動跟蹤控制系統的設計[J]. 東北電力技術, 2013, 3: 48－50

[4] 張鵬飛. 光伏發電自動跟蹤系統的設計[D]. 哈爾濱理工大學, 2009, 23－24

[5] 張宏. 布爾莎-沃爾夫轉換模型的幾何證明[J]. 測繪與空間地理信息, 2006, (2): 52－53．

[6] (西 )Antonio Luque, (美 )Steven Hegedus, 等 [著 ], 王文靜 ,李海玲, 周春蘭, 等[譯]. 光伏技術與工程手冊[M]. 北京: 機械工業出版社, 2011．