基于de Bruijn圖的M序列遞歸升級構造方法

郭 輝，柏 森，陽 溢，宋 斌，李淑云

(1．重慶通信學院信息工程系，重慶400035;2．應急通信重慶市重點實驗室，重慶400035;3．解放軍66019部隊，北京100093)

1 概述

M序列是由非線性反饋移位寄存器產生的周期最長的序列，也稱為de Bruijn序列。由于M序列具有偽隨機性、周期性、均衡性、相位相加性、自相關等特性［1-4］，并且隨著級數的增大，M序列的數量呈指數級增多，因而被廣泛應用在衛星保密通信［1］、擴頻通信抗干擾［2］、系統識別［3］、信息隱藏［4］等方面。雖然目前有了一些生成M序列的方法，但對M序列的研究還不很成熟，關于它的生成方法及性能尚無完整的理論分析。

目前，M序列的生成方法主要有生成樹法［5］、并圈法［6-8］、查詢表標簽法［9-10］、計算機搜索算法［11-12］等。值得注意的是文獻［13-15］提出了M序列的升級算法。文獻［13］提出了一種查詢表標簽的升級算法，通過給定的n級M序列的查詢表標簽，采用合成的方法構造出n+1級M序列的查詢表標簽，從而產生n+1級M序列。但查詢表標簽的構造較復雜，實現有一定的難度。文獻［14-15］給出了二元n級M序列的升級算法，在已知低級M序列反饋函數條件下，求高級M序列的反饋函數。文獻［16］給出了求反饋函數的升級算法，通過定義環F2+μF2上的n級de Bruijn圖到n－1級de Bruijn圖的滿同態映射D，證明一個由環F2+μF2上n－1級M序列的反饋函數產生n級M序列反饋函數的升級算法定理。文獻［17］給出了k元n級de Bruijn序列的反饋函數的一個升級算法，該算法定義了k個從k元n級de Bruijn圖到k元n－1級de Bruijn圖的滿同態映射，利用這些同態映射，從一個n－1級k元de Bruijn序列的反饋函數直接生成k個k元n級de Bruijn序列的反饋函數;進而給出了一個從二元n－2r級de Bruijn序列反饋函數直接生成二元n級de Bruijn序列的反饋函數。

上述升級算法只在理論上進行了分析，而沒有給出具體的實驗結果。這些算法存在的局限性:或是不能生成全部的M序列;或算法復雜度高，且當n較大時，運行效率較低;或是不能生成任意級數任意數量的M序列。由于高級M序列數量巨大，生成全部的M序列需要大量的時間。文獻［18-20］對快速生成一條M序列進行了研究。遺傳算法［18］把M序列作為一種特殊的旅游銷售員問題(TSP)，并嘗試找到最佳的觀光路徑。首先，用隨機式或探索式二種方法之一產生初始的觀光路線集合。其次，利用公式計算集合中節點的2個相鄰節點與此節點的長度之和，長度大于2的節點相互交換位置，直到產生最理想的或者沒有最理想的觀光路線為止。最后，重復以上2種操作500次，輸出產生的所有最理想的觀光路線集合。當n較大時，只能產生一條M序列，文中把遺傳算法看做生成一條M序列的方法。存在的局限性:(1)由于算法中產生初始觀光路線的方法為隨機方式，所以不一定產生n級的所有M序列，且產生的M序列不具有唯一性。(2)當級數較大時，算法效率較低。文獻［19-20］給出了 Prefer-one和Prefer-opposite算法，Prefer-one算法［15］采用的是直接添值方法，產生一個n級M序列，首先設置n個0，后面添加1，如果任意相鄰的n位沒有出現與之相同的數，則添加數保留，否則添加0。直到添加1或者0沒有新的數值出現，算法結束。存在局限性:(1)形式固定，M序列添加的前n位一定是1;(2)只能產生一條M序列。Prefer-opposite算法［20］也是采用直接添值的方法，添值為上一位的相反數。首先設置n個0，后面添加最后一位0的相反數1，如果任意相鄰的n位沒有出現與之相同的數，則添加數保留，否則添加和最后一位相同的數。直到添加1或者0沒有新的數值出現，算法結束。本文算法存在的局限性:(1)算法不能產生全1的狀態;(2)形式固定，M序列最后n位一定是1;(3)只能產生一條M序列。2種算法相比，Prefer-one算法產生的M序列前部分1的數量要多，對于級數n=59的 M序列，前106位90%為1。Preferopposite算法產生的M序列傾向于1和0的平衡，對于級數n在10～20之間，M序列的前1/4位0和1的比例更接近50%。

本文在圖論知識的基礎上，給出一種隨機生成一條二元高級M序列的方法。首先任意給出一條二元n級M序列，此M序列轉換為二元n級de Bruijn圖中的一條Hamilton回路;其次求圖中此Hamilton回路的補路，補路由自環和不同長度圈組成，補路中自環和各圈隨機選取一個點，按照此點在原Hamilton回路中的位置插入自環和各圈，從而得到n級de Bruijn圖的Euler回路。最后，由Euler回路構造成n+1級M序列。按照此方法，依次遞歸，求出所需的高級M序列。

2 Hamilton，Euler回路與M 序列的關系

2．1 de Bruijn圖的構造方法

二元n級de Bruijn圖是二元n級M序列的所有可能狀態轉移的一種圖像表示。要構造一個二元n級de Bruijn圖，簡單表示為 Gn(2)，設n≥2，Z2={0，1}，構造有向圖Gn(2)。首先要確定圖的頂點數和頂點值，一個二元n級M序列共有2n個狀態，把每個狀態(b1，b2，…，bn)(bi∈Z2)作為特殊有向圖Gn(2)中的一個頂點。進而，對2個頂點B=(b1，b2，…，bn)和 C=(c1，c2，…，cn)，如果 B 的后 n －1位依次為 C 的前 n－1 位，即(b2，b3，…，bn)=(c1，c2…，cn－1)，則圖中便引一條弧 B→C，并且為這條弧添加一個標記，即這條弧為(b1b2…bncn)=(b1c1c2…cn)。所以特殊有向圖Gn(2)中共有2n個頂點，并且以每個頂點vi為始(終)點的弧數目均為2，即頂點vi的出度和入度均為2。圖1和圖2分別為構造的有向圖G2(2)和G3(2)。

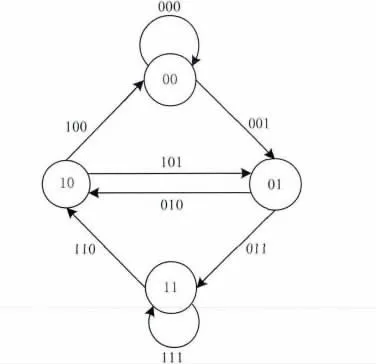
圖1 有向圖G2(2)

圖2 有向圖G3(2)

2．2 Hamilton，Euler回路及其表示方法

經過圖G中每個頂點一次且僅一次的回路稱為G的Hamilton回路。在Gn(2)圖中，一個有限非空序列Γ=v0e1v1e2v2…ekvk，它的項交替地為頂點和弧，使得對 1≤i≤k，ei的端點是 vi－1和 vi，頂點 v0和 vk分別為起點和終點，則稱Γ是從v0到vk的一條通路，若除起點v0和終點vk外，其他頂點各異且歷經了每一個頂點，則稱Γ為圖Gn(2)的Hamilton回路。

經過連通圖G的每條弧一次且僅一次的回路稱為Euler回路，或者Euler閉跡。在Gn(2)圖中，一個有限非空序列Γ=e0v0e1v1e2…vkek，它的項交替地為弧和頂點，并經過所有弧一次且僅一次，且弧ek的終點vk為e0的起點則稱Γ為Euler回路。在圖中弧和頂點有著緊密的聯系，弧也可以由頂點來表示。例如在圖1中一條弧，可以用頂點表示為00→01。在Gn(2)圖中每個頂點的出度和入度都為2，一個Euler回路還可以表示為一個有限非空序列Γ=v0e0v1e1…vkekv0，它經過每條弧一次且僅一次，經過每個頂點兩次，又回到原來的頂點。如圖1中，一條Euler回路為弧，可以用頂點表示為00→00→01→10→01→11→11→10→00。

2．3 Hamilton回路、Euler回路與M序列的關系

在Gn(2)圖中，一條Hamilton回路為二元n級M序列，一條Euler回路為二元n+1級M序列［21］。例如:在圖 1中，00→01→11→10→00為一條Hamilton 回路，它的頂點依次為 00，01，11，10，通過提取每個頂點的最高位的值，可以得到一個二元2級M序列 0011。一條 Eular回路為弧序列，它經過的弧依次為，提取每條弧的最高位的值得到二元3級M序列00010111，此 Euler回路由頂點表示為:00→00→01→10→01→11→11→10→00，它的頂點一次為00，00，01，10，01，11，11，10 提取每個頂點的最高位的值得到二元3級M序列00010111。由上可知，由一條二元n級M序列求二元n+1級M序列，等同于已知二元n級Gn(2)圖中的一條Hamilton回路求與之相關的Euler回路。

3 生成M序列的遞歸升級算法

3．1 圖Gn(2)中的Euler回路

已知圖Gn(2)中的一條Hamilton回路，求與此Hamilton回路相關的Euler回路(頂點表示)，只需要求出此Hamilton回路的補路，并在相應位置插入補路即可。如圖3所示，實線部分為一條Hamilton回路，只需要求出此Hamilton回路未歷經的弧，即求出此Hamilton回路的補路，在對應位置插入補路即可求出Euler回路。

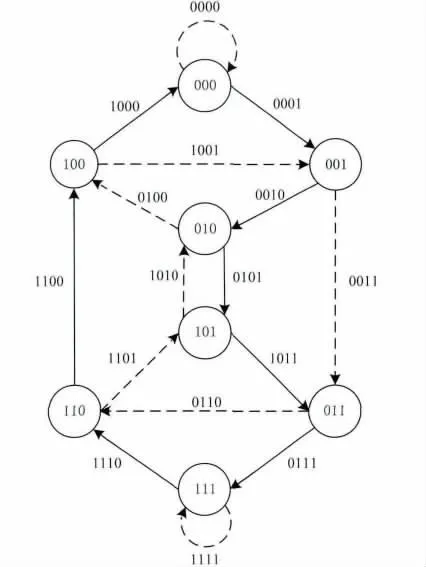
圖3 有向圖G3(2)的一條Hamilton回路

(1)求Hamilton回路的補路。首先，任意設置一個頂點為補路的起點。其次，此頂點的后繼頂點為未在Hamilton回路中直接連接的、且有有向弧直接連通的另一個頂點(如圖3虛線部分所示)，查找方法為此頂點在Hamilton回路中的后繼頂點最后一位與1異或而得到補路的后繼頂點，依次遞歸，直到形成回路為止。如果此回路的長度小于2n，任意設置一個未出現在補路的頂點為起始點求補路，直到形成回路，按照此方法直到各回路的長度和為2n次方為止。通過觀察和驗證發現，Hamilton回路的補路共由兩部分組成:一部分為自環(長度為1的圈)，全0和全1頂點有自環;另一部分為圈，除自環外其他頂點組成不同長度的圈(當n大于5時，圈的個數逐步增多)。如圖3，是一個二元3級de Bruijn圖，它的一條Hamilton回路(實線所示)000→001→010→101→011→111→110→100→000。此 Hamilton回路的補路(虛線所示)為:自環有000→000和111→111，圈為一條長度為6的回路001→011→110→101→010→100→001。

(2)Euler回路的求法。按照上述方法求出補路，通過插值方法把所求補路添加到Hamilton回路中得到Euler回路。插值方法是在補路中的自環和各圈中任找一個頂點，在Hamilton回路中找到對應點插入自環和各圈即得到Euler回路。如圖3所示，已知一條 Hamilton回路000→001→010→101→011→111→110→100→000，求得補路，自環有000→000和111→111，圈為一條長度為6的回路001→011→110→101→010→100→001。自環只有一個點直接插入得到的頂點序列為:000→000→001→010→101→011→111→111→110→100→000，圈為一條有6個頂點的回路，每一個頂點在對應的位置插入圈都可以得到一條不同的Euler回路，假設選擇的頂點為011，在頂點序列中找到頂點011，在此位置插入以頂點011開始的圈，得到的頂點序列為000→000→001→010→101→011→110→101→010→100→001→011→111→111→110→100→000，此頂點序列即為Euler回路。

補路中每個圈的插值方式共有a(圈頂點個數)種，各圈共有各圈頂點數的乘積種不同的插值方式，所以一條Hamilton回路可以產生Euler回路的個數由補路中各圈頂點個數的乘積決定。在圖3中，補路的圈只有一個，圈頂點的個數為6，所以可以產生6條Euler回路。例如:一個二元4級M序列000010 1111001101，在二元4級de Bruijn圖中轉換為一條Hamilton回路，求得補路為:自環為:0000→0000和1111→1111;圈為:(1)0001→0011→0111→1110→1101→1011→0110→1100→1000→0001;(2)0010→0100→1001→0010;(3)0101→1010→0101。各圈的頂點個數分別為9，3和2，所以此Hamilton回路可以產生54條Euer回路。

3．2 遞歸升級算法的基本思想及步驟

3．2．1 遞歸升級算法的基本思想

從2．3節可以看出，求一條低級M序列是比較簡單的。在已知一條低級M序列的條件下，如何通過遞歸升級的方法構造高級M序列。本文的基本思想是:已知一條低級M序列，將其轉換為在de Bruijn圖中一條Hamilton回路，通過求補路的方法求出補路，按隨機插值的方式，在Hamilton回路中插入補路得到Euler回路，構成二元n+1級M序列，依次遞歸升級構造高級M序列。具體過程如下:首先，任意給出一條低級二元n級M序列，并在二元n級de Bruijn圖中畫出此M序列的Hamilton回路，為了便于計算，各頂點值用十進制表示。其次，求出此Hamilton回路的補路(按照3．1節的方法求出)。最后，補路中各圈隨機選取一個頂點，并在Hamilton回路中找到此頂點，補路中各圈在對應位置插入Hamilton回路中，在全0頂點和全1頂點位置對應插入全0和全1的自環，得到Euler回路，構成二元n+1級M序列。按照此方法依次遞歸生成所要的高級M序列。

隨機插值方法主要是為了解決補路中各圈的頂點選取問題。首先，確定補路各圈的個數以及各圈中頂點的個數;然后，依次用隨機函數產生一個0到1的隨機數，各圈的頂點數乘以對應的隨機數，并取整即得到各圈中選取頂點的位置，找出此頂點。

3．2．2 遞歸升級算法步驟

本文算法步驟如下:

Step1任意給出一條M序列，由M序列的長度l求出所給M序列的級數m。輸入n的值，此為所求M序列的級數。

Step2如果n大于m繼續下面的操作;否則，停止。

Step3依次列出M序列的2m個狀態序列，并轉換為十進制，狀態序列用L表示。

Step4任意設置狀態值v1為第1個頂點，在L中找到v1點的后續狀態v'2，v'2的最后一位和1異或，得到的值為v2，重復上述操作，直到vn=v1。如果求得的狀態序列長度小于2m，設置一個所求狀態序列中未出現的狀態值vi為另一條狀態序列的起始點，按照上面的方法，求出各狀態序列，直到生成的狀態序列的長度和為2m為止。

Step5M序列的補路隨機插值在狀態序列L中，構成Euler回路的狀態序列。依次用隨機函數產生0到1的隨機數，乘以對應的頂點序列的頂點數，并取整，得到各序列的選取狀態值的位置，找到此狀態值，并在L中找到該狀態值，在狀態位置插入相應的狀態序列，得到的狀態序列為FB。

Step6提取FB的前2m個狀態值的最高位，得到m+1級M序列。m=m+1，返回Step2。

4 實驗結果及分析

4．1 實驗結果

仿真計算機為 XP操作系統，CPU主頻為2．79 GHz，內存1．75 GB，用 Matlab 仿真軟件編程測試。假設給出的一個二元2級M序列0011，利用遞歸升級構造法隨機生成一條n級M序列，當級數n=11，12，…，20時，算法運行結果如表1所示。表中，“碼長”表示M序列中0，1的個數，“空間大小”為生成的n－1級M序列可以生成n級M序列的個數，“耗時”為生成n級M序列所需時間。

實驗結果表明，本文算法能夠隨機生成一條高級M序列，而不用生成全部的M序列，大大節約了時間和資源。產生的M序列隨機性強，每一個n級M序列可以生成多條n+1級的M序列，依次遞歸產生的高級M序列會增多，樣本空間巨大，產生的一條M序列采用隨機的方式在樣本空間中選取，隨機性強。

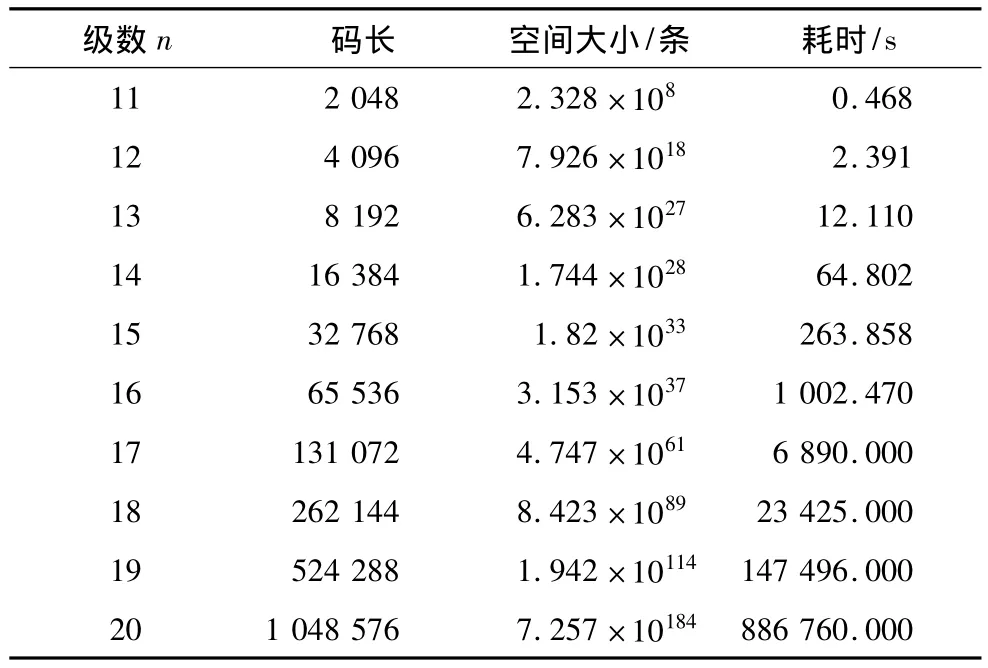
表1 遞歸升級算法生成的n級M序列

4．2 與其他算法的比較

當M序列的級數n＞10，本文算法與遺傳算法［18］、Prefer-one 算法［20］、Prefer-opposite 算法［21］在成功率、有效性、空間大小進行比較，如表2所示。

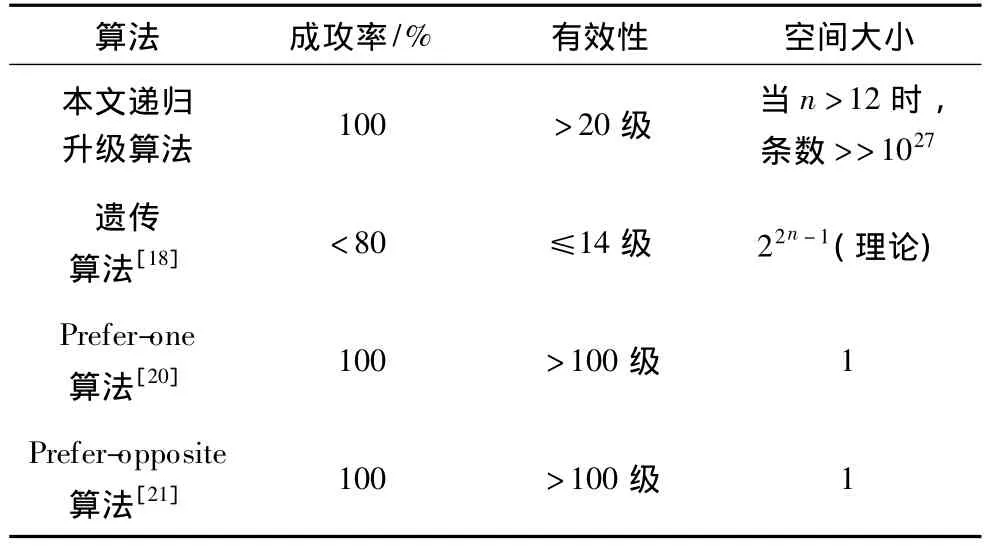
表2 遞歸升級算法和其他算法比較

本文算法優點如下:

(1)成功率高，成功率為100%。任意一條M序列都能通過在de Bruijn圖中求補路的方法求出補路的自環和各圈，用插值的方法能夠產生高一級的M序列。

(2)有效性大于20級。當n＞20時，生成一條高級M序列的時間較長，理論上算法可以產生任意級數的高級M序列。

(3)樣本空間大。每級的M序列求得的補路中圈的個數及各圈的頂點數可能不同，所以不能從算法中直接求出空間的大小，但一條M序列可以多條高一級的M序列，多條高級M序列依次遞歸，產生的M序列的數量也是巨大的。

4．3 隨機性測試

本文采用美國國家標準和技術研究所的NIST SP800-22 測試標準［22］，用 sts-2．1．1 測試軟件對遞歸升級算法生成的M序列進行隨機性能測試。測試標準共包含15個測試項，當p－value≥0．01時，測試的M序列被認為是隨機的。測試序列為任意生成的一條二元20級M序列，共有1 048 576個碼元，測試結果如表3所示。

表3 NIST SP800-22測試結果

測試結果表明:提出的遞歸升級算法生成M序列的各測試值都大于0．01，滿足隨機性的要求，且多項值在0．5以上，隨機性能較好。Frequency Test的測試值為1，表明整個序列中0和1的個數相等，在序列中所占比例各為0．5;Runs Test的測試值為1，表明序列中0游程和1游程的個數相等，與理想的隨機序列的期望值相一致;Serial Test的測試值為1，表明序列有較好的均勻性，對于每一個長度為m的子序列，不同模式的子序列出現的概率是相等的;Approximate Entropy Test測試的檢驗手段是看線性反饋移位寄存器的長度，隨機序列的特點是有較長的線性反饋移位寄存器，線性反饋移位寄存器太小說明序列為非隨機的，測試值為1，說明序列有較長的線性反饋移位寄存器長度，復雜度較高。

5 算法時間復雜度分析

本節從M序列的構造過程對時間復雜度進行分析。在求高級M序列的過程中，需要從低級逐級遞歸到高級，時間復雜度為O(n)=n，問題規模為n。在求M序列的狀態序列過程中，采用的是按順序求值的方法，時間復雜度為 O(n)=2nn。在求M序列補路的過程中，采用順序查找的方法，時間復雜度為O(n)=2n+1。在求Euler回路的過程中，采用隨機插值的方式，時間復雜度O(n)=2n。則算法復雜度O(n)=n22n+n2n+1+n2n，為指數復雜度。雖然算法效率不夠好，但對于高級M序列具有較大的問題規模，且解決難度較大的情況下，該算法的復雜度能夠滿足解決M序列生成問題。可得出結論，本文算法的復雜度能夠有效地生成M序列。

6 結束語

本文根據de Bruijn圖中Hamilton回路和Euler回路的關系，給出了M序列的遞歸升級算法，算法簡單有效，易于實現，在圖像加密等領域有一定的應用前景。但該算法也存在算法復雜度高的不足，針對該問題，下一步的主要工作是研究一種更加有效生成M序列的方法以及M序列在信息安全領域的應用。

［1］ 袁俊華，邵 偉．M序列碼的特性及在GPS導航通信保密中的作用［J］．內燃機與動力裝置，2009，(S1):47-50．

［2］ 趙宗民．基于63位 M序列的擴頻通訊系統的設計［D］．天津:天津大學，2007．

［3］ 向曉燕，孟凡斌，張書真．M序列在系統辨識中的應用［J］．信息與電腦:理論版，2010，(11):29．

［4］ 劉志軍．基于 M序列與 Word文檔的信息隱藏算法［J］．通信技術，2009，42(7):113-115．

［5］ 萬哲先，代宗鐸，劉木蘭，等．非線性移位寄存器［M］．北京:科學出版社，1978．

［6］ 金 玥，余海峰．產生2元 M序列的一個新算法［J］．合肥學院學報:自然科學版，2007，17(3):4-5．

［7］ 芮義鶴．二元deBruijn序列的一個生成算法［J］．合肥工業大學學報:自然科學版，2009，32(1):139-141．

［8］ 朱士信．產生M序列的一個遞推算法［J］．信息安全與通信保密，1995，6(3):18．

［9］ 謝深泉．de Bruijn序列查尋表標簽的定值構造法［J］．計算機工程與應用，2008，44(19):37-40．

［10］ 謝深泉．de Bruijn序列查尋表標簽的末位基準構造法［J］．小型微型計算機系統，2009，30(9):1819-1823．

［11］ 趙群依，劉順蘭，王江柱．一種de Bruijn序列的高效生成算法［J］．通信技術，2007，10(11):302-303，402．

［12］ 王 誠，吳 蕾．任意長度的 M 序列的生成［J］．西安電子科技大學學報，2001，28(1):129-132．

［13］ 謝深泉．生成de Bruijn序列的升級算法［J］．計算機工程，2008，34(24):213-215．

［14］ 張 霞，吳 波．環F_2+uF_2上de Bruijn序列的一個有效升級算法［J］．中國科學技術大學學報，2009，39(6):594-598．

［15］ 朱士信，孫 琳．k元 de Bruijn序列的反饋函數的一個升級算法［J］．電子學報，2006，34(6):1066-1068．

［16］ Annexstein F S．Generating de Bruijn Sequences:An Efficient Implementation［J］．IEEE Transactionson Computers，1997，46(2):198-200．

［17］ Chang T，Park B．An Efficient Implementation of the D-homomorphism for Generation of de Buijn Sequences［J］．IEEE Transactions on Information Theory，1999，45(4):1280-1283．

［18］ Sonmez T M．Evolutionary Construction ofde Bruijn Sequences［C］//Proceedings of the 4th ACM Workshop on Security and Artificial Intelligence．New York，USA:ACM Press，2011:81-86．

［19］ Alhakim A M．A Simple Combinatorial Algorithm for de Bruijn Sequences［J］．American Mathematical Monthly，2010，117(8):728-732．

［20］ Fredricksen H．A Survey of Full Length Nonlinear Shift Register Cycle Algorithms［J］．SIAM Review，1982，24(2):195-221．

［21］ 馮克勤．數論與密碼［M］．北京:科學出版社，2007．

［22］ Rukhin A，Soto J，Nechvatal J，et al．A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications［M］．Mclean，USA:Booz-Allen and Hamilton Inc．，2001．