基于信任度的并行化社區發現算法

余紫丹，虞慧群

(1．華東理工大學計算機科學與工程系，上海200237;2．上海市計算機軟件評測重點實驗室，上海201112)

1 概述

社交網絡作為人類最復雜的網絡之一，與其他的網絡的不同之處在于，它是由多個社區組成的。社區形成的原因多種多樣，但社區最重要的基礎，是信任關系。信任是人類社會活動的基石，社區內的信任關系維系了社區的存在、發展。

目前社會性網絡中對信任的研究還處于起步階段，研究成果較少，鮮有提供準確計算信任度的度量方法。文獻［1］提出利用FOAF(Friend of a Friend)在基于Web的社交網絡中計算沒有直接聯系用戶之間的信任度關系，但是其信任度僅有信任、不信任兩種取值使其很難用于現實的社交網絡環境中;文獻［2］提出了在基于地理位置的社會性網絡中結合鏈接關系與社會聲譽來決策信任度的機制，但該機制只適用于特定的網絡，缺乏普適性。文獻［3］提出的PGP(Pretty Good Privacy)模型把信任的主動權留給用戶自己，通過基于推薦者的網狀信任模型來進行信任等級的判斷。

然而，在PGP的信任模型內，信任鏈的長度最大為2，信任度衡量粒度也只有信任、不信任2種選擇，難以應用在社交網絡上。針對于此，目前已有不少根據信任推薦模型的社交網絡信任度計算方法，例如文獻［4］提出一種如何挑選可信賴用戶進行信任推薦的算法。文獻［5］利用節點之間的鏈接關系來發現2個目標用戶之間的最優可信信任路徑，但未考慮次要信任路經對兩者信任關系帶來的影響。但是，由于社交網絡中用戶的組織關系比較復雜，多數由PGP模型發展而來的基于信任推薦的算法，對信任推薦的路徑復雜度予以回避，或者只考慮一個中間推薦者的情況，沒有對存在多個中間推薦者、形成多信任推薦路徑組合的情況進行考慮;又或者只能適用于小規模數量的網絡。為了解決在大規模社交網絡下的多信任推薦路徑組合的復雜情況，必須利用并行化的計算方法，統一考慮所有信任推薦路徑的情況。

Hadoop是Apache基金會基于MapReduce計算模型而完成的一個處理大規模數據的分布式系統架構。它提供了高可靠的分布式存儲系統HDFS和一種分布式計算平臺，用戶只要實現相應的 Map、Reduce函數即可實現高性能的分布式算法，而不必過多了解底層細節。函數必須滿足Map函數的輸出與Reduce函數的輸入類型相同。

本文根據社交網絡內社區的特點，在現有的點對點之間信任模型的基礎上，結合傳統在P2P領域的經典算法，提出計算社交網絡上用戶間信任度的方法，并在此基礎上進行社區擴散，最終所有節點所屬社區趨于穩定，并得到最終的社區劃分結果。由于計算機內存限制及算法復雜度較高，本文利用MapReduce計算框架來解決這一問題。

2 算法設計

本文是針對大規模社交網絡而提出的一種并行化的基于信任度的社區劃分算法，用途在于分析類似于微博這樣的社交網絡內部的社區結構，以幫助發現網絡隱藏規律和預測變化。在此首先介紹信任度的計算方法，然后描述算法整體框架，針對框架中每個模塊涉及到的MapReduce過程，給出對應設計及偽代碼實現。

2．1 信任度的傳播與計算

首先構建一個社會網絡有向無權圖G=(V，E)，其中V表示頂點(用戶)集合，且共有|V|=n個用戶節點，E表示用戶有向關系的集合，eij表示連接vi，vj2個頂點的邊。若eij=1，則說明節點vi到節點vj之間存在著一條邊，也就說明用戶i對用戶j進行了關注，用戶i對用戶j有一個信任關系。

目前關于社交網絡內的信任及其一些特性并沒有權威的定義，本文首先對信任作如下假設:

假設1一個用戶節點在初始時，共有總和為1的信任額度，且平均分配給其所有關注著的用戶;

假設2任意2個用戶之間的信任度，是由他們之間的所有信任推薦路徑決定的。一條路徑上的信任度會逐漸衰減，多條信任路徑上的信任度會疊加。

根據這兩條假設，易得如下推論:

推論1若用戶i對用戶j進行了關注，而用戶i共關注了個用戶，則i對j的初始信任度為:

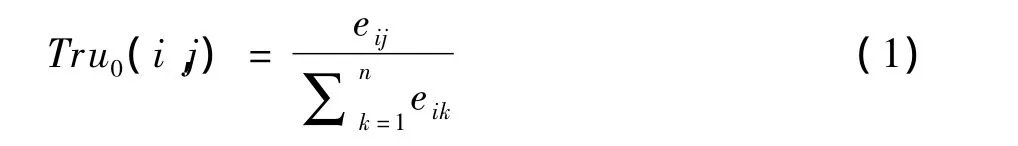
特殊的，不考慮用戶自己對自己的信任情況，即Tru0(i，i)=0。

推論2信任度能以2種方式傳播:串聯，并聯。串聯會隨著中間節點的增加而衰減，以圖1中第1種傳播方式為例，得到用戶1對用戶4的信任度為:

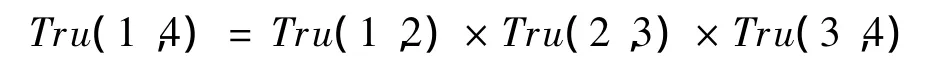
并聯會導致信任度隨著路徑的疊加而增加，以圖1中第2種傳播方式為例，得到用戶1對用戶8的信任度為:

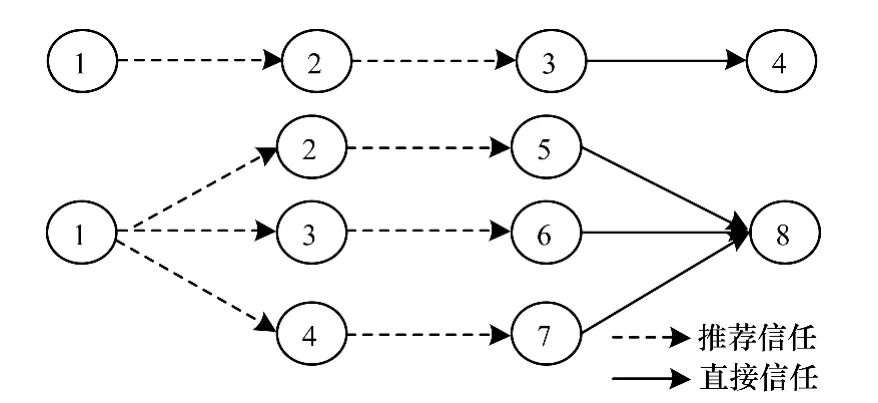
圖1 信任度傳播方式

所以，對于任意2個節點，必須先找到這2個節點之間所有可能的信任推薦路徑，然后再根據串行、并行的不同給出信任度最終結果。

然而，在真實的社交網絡中，信任推薦路徑并不是可以任意長度的，根據六度分隔理論，人們最多通過5個中間人就能互相認識，事實上，現實世界中的信任隨著信任鏈的長度的增長而迅速衰減［6］。本文假設信任推薦路徑的長度最大為4，也就是最多經過3個中間人的信任推薦是有效的。盡管對路徑長度的限制縮小了信任推薦路徑的可能性，但針對任意2個用戶，通過深度優先搜索，來窮盡他們的所有可能的信任推薦路徑，從算法復雜度來講是不可取的。

對于之前描述的社交網絡圖而言，若將該網絡G分成k份，分別為k個節點集合φ={N1，N2，…，Nk}。若該劃分具有對于每個Ni∈φ，都滿足Ni內的節點信任鏈密集、與Ni外信任鏈稀疏的特性，則稱φ為G的基于信任鏈的社區劃分。

從上面關于信任度的概念可以知道，最初始的信任度矩陣只與圖的鄰接矩陣有關，由于鄰接矩陣為:

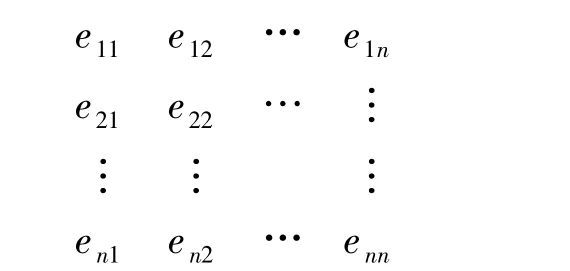
因此可以得到初始信任度矩陣為:

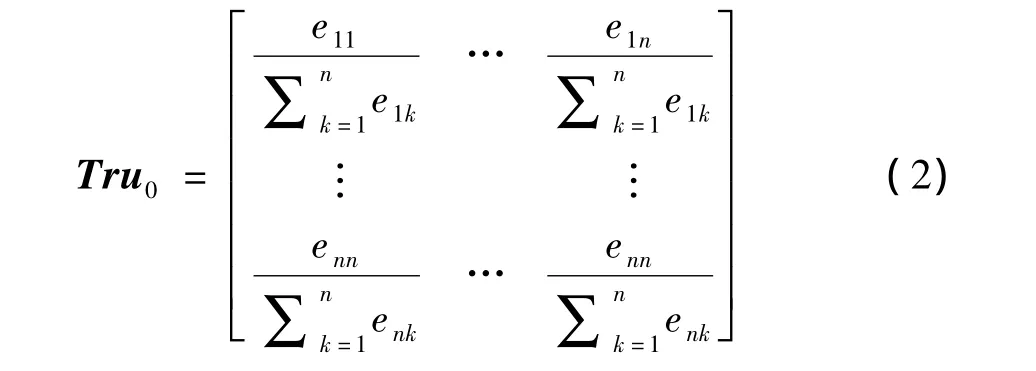
接下來考慮存在著一個中間推薦者來進行信任度間接傳播的情況，用戶 i，j，考慮經過節點{1，2，…，n}信任鏈路徑，可得:

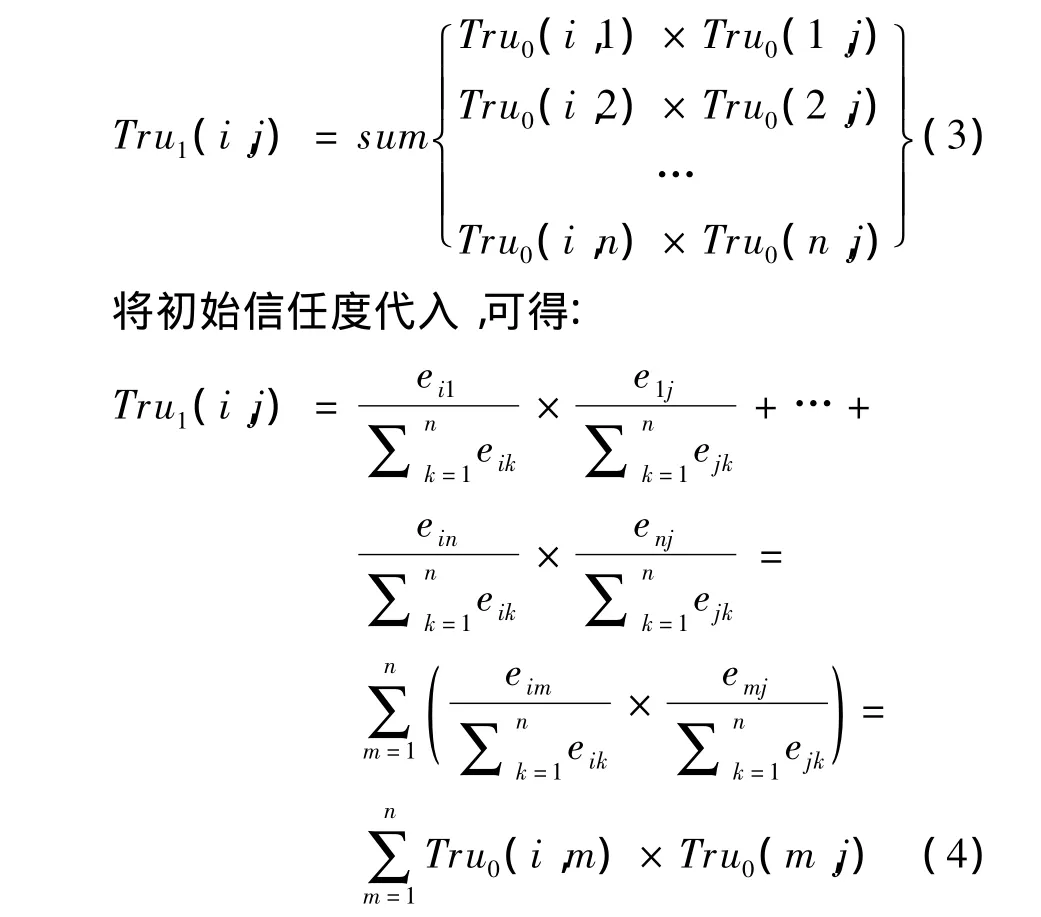
這等價于2個初始信任度矩陣相乘后的矩陣上［i，j］元素，直觀的角度來看，初始信任度表示了用戶之間的信任關系，可以畫成一個二部圖，而當2個初始信任度矩陣相乘時，可以將這樣的信任傳播過程可以畫成如圖2所示的三部圖。Tru1(i，j)的幾何含義，便是節點i到節點j之間所有可能的信任推薦路徑上的權值之和。類似的，若考慮用戶i，j存在著2個中間推薦者來進行信任度間接傳播的情況，則如圖3所示。

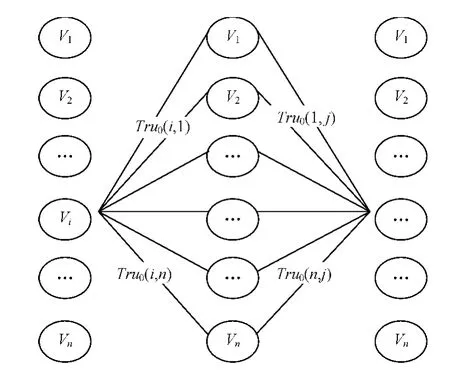
圖2 初始信任度矩陣相乘時形成的傳播圖

圖3 存在2個中間推薦者時的信任傳播圖

用戶i，j需要尋找2個中間節點來做信任推薦，可以得到:

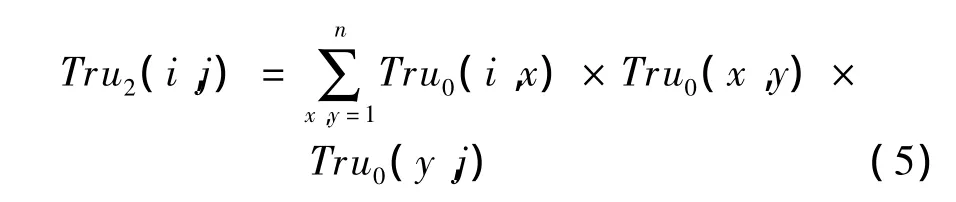
這等價于3個初始信任度矩陣相乘后的矩陣上［i，j］元素。

以此類推，可以得到:Truk=(Tru0)k+1。

這樣，就得到了最終的信任度計算公式:

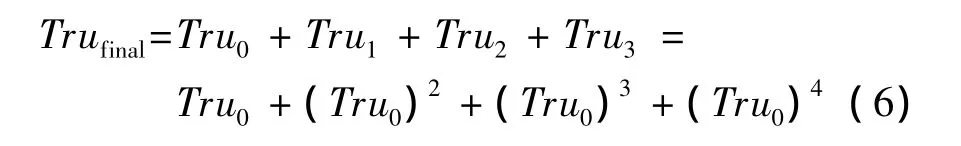
這樣，問題就從路徑搜索問題，轉換為大矩陣相乘問題。

2．2 算法整體框架

在得出如何求解任意2個用戶之間的信任度后，給出如下的算法框架，對基于信任度的并行化社區算法予以描述。

如圖4所示，該算法首先通過用戶之間的關注關系構造初始信任度矩陣，并且通過信任度的兩種傳播方式來更新信任度矩陣，然后在最終形成的信任度矩陣上，通過社區標簽的迭代擴散，得到最終的社區劃分矩陣。

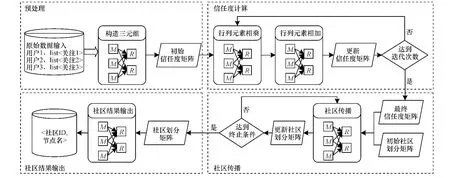
圖4 算法整體框架

圖4中M和R表示MapReduce過程中的Mapper和Reducer。下面對這4個步驟的算法作簡要說明。

2．2．1 數據預處理模塊

一般從社交網絡上得到的數據是以＜User ID，follower 1，follower 2，…＞這樣的格式存儲在文本中的，每一行都是一個用戶及他所關注的所有對象。社交網絡的矩陣維度一般在千萬級別，其內部十分稀疏。故利用MapReduce并行化處理文本，轉為初始信任度矩陣，采用三元組存儲。偽代碼如下所示:

2．2．2 信任度更新模塊

信任度矩陣公式本質是大矩陣的乘法運算，參考文獻［7］及式(7):

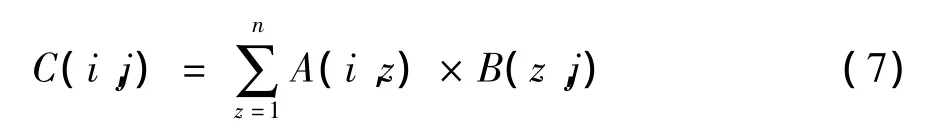
給出一種大規模矩陣乘法算法，通過2輪MapReduce，在第1輪中，將矩陣A的行元素與矩陣B的對應列元素相乘，在第2輪中，將相乘的結果累加起來，形成更新后的信任度矩陣。大規模矩陣乘法的流程如圖5所示。

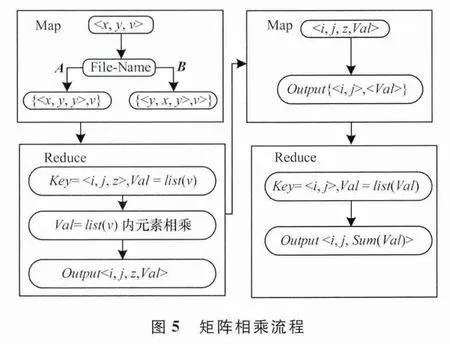
在這樣的矩陣乘法基礎上，給出如下偽代碼，以進行信任度矩陣的迭代計算，并通過累加，得到最終信任度。

2．2．3 社區傳播模塊

在得到用戶兩兩之間的最終信任度后，這里給出一種社區劃分的算法，首先賦予每個節點一個獨立的社區id，在每一輪迭代時，每個節點的社區id由其信任的那些節點決定，信任度越大對該節點的影響越大。通過這樣的社區id更新，相互信任度較高的節點集合會迅速對社區id達成共識，形成社區。每輪迭代只依賴于上一輪的社區id分配結果，利用三維數組＜User id，Community id，w＞將社區分配存儲下來，w是用戶被分配到該社區的強度，初始值為1，在迭代過程中與信任度相乘，并更新。若每一條數據分配12個字節，可以表示三維數組每維范圍為［1～232］，足以記錄千萬用戶數量級時的社區分配情況，在數據規模千萬級時需要百兆級別的內存，故可以在每輪迭代前將用戶的社區id分配結果放在內存中，通過get-Social-Id(User id)這樣的方法讀取。然后在Mapper端計算一個節點所有可能的社區id，并更新其對應的權重，在Reducer端完成對社區id的選擇，當各用戶的社區id分配穩定后(更改社區id的用戶數量小于用戶總數n×10-3)循環終止，在得到最終的社區id分配，并將其輸出。用戶節點更新社區id的偽代碼如下:

2．3 算法分析

算法采用信任度推薦者模型迭代計算任意2個用戶的信任度，然后在此基礎上采用社區傳播的方式進行社區劃分，相較于傳統的直接在網絡關系圖上進行圖聚類的算法而言，本文算法在第一輪的迭代過程中，加強了簇內用戶之間鏈接關系，而在第2輪的迭代過程中，處在簇內中心位置、與周圍信任度都較高的節點，會迅速將簇標簽信息(社區ID)傳播到整個簇內用戶節點，使得社區結構自然地呈現出來。

本文算法的復雜度，主要取決于迭代過程中計算大矩陣乘法的復雜度。通過針對矩陣乘法設計的偽代碼可知，若令No［Ai］代表矩陣A的第i行中非零值的個數，則本文所用稀疏矩陣相乘算法的時間復雜度為，與矩陣的實際稀疏程度相關。

3 實驗與結果分析

3．1 實驗環境及實驗數據

本文實驗在由10個節點組成的Hadoop集群上進行，集群中每臺機器硬件環境相同，配置信息如表1所示。

表1 集群基礎配置

清華大學唐杰教授通過隨機抽取100個新浪微博用戶，抓取他們的關注者和粉絲，并最終發布了一個有1 787 444個用戶節點、308 489 739條關注關系的社交網絡數據［8］。

此外，還有一些經典的小型社交網絡數據集［9］，Zachary數據集為美國一所大學的空手道俱樂部成員間關系的網絡;LesMis數據集為《悲慘世界中》人物關系網絡;Dolphin數據集為62只海豚組成的種群中，各成員交流頻度的社交網絡［10］。

3．2 精準度對比

首先在數據集上證明本文算法劃分社區的準確性，針對各類數據集，應用本文算法與傳統的Label-Propagation算法、Random-Walk算法和 Fast-Greedy算法進行實驗［11］，以證明本文算法社區劃分的準確度。這3種傳統算法均是針對單機環境設計完成的。由于Random-Work算法需要計算任意2個節點之間的距離，而Fast-Greedy算法需要迭代計算整體網絡圖的模塊度值，隨著節點數目的增加，這2種算法導致的時間耗費越來越大，在面對大規模微博數據集時，不能夠在有限的時間內完成。相對的，LP算法由于有著接近線性的時間復雜度，不需要計算復雜的優化公式，因而在微博數據集下，只令本文算法與LP算法進行比較。

社區劃分并無準確的判斷標準，現行的常見做法是采用Q函數［11］來評判社區的質量，具體結果如表2所示。由實驗結果可知，本文算法在Q函數評價標準下，較LP，RW，FG算法而言，有著更好的社區劃分效果。

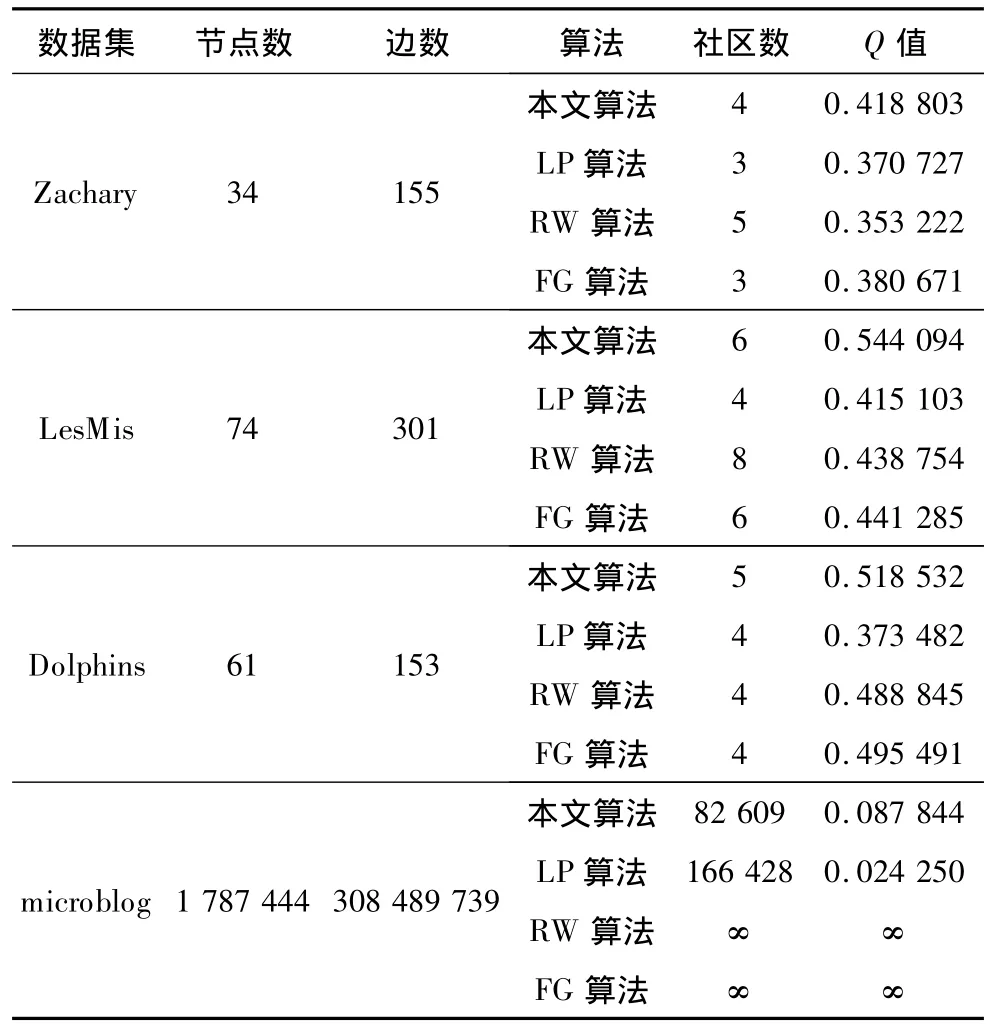
表2 各數據集上實驗結果比較

3．3 可擴展性

3．3．1 運行時間隨數據集大小的變化

將微博數據集上所有的節點分為10份，每輪實驗分別輸入1份 ～10份數據，觀察算法隨數據規模變化所耗費的時間，實驗結果如圖6所示。其中，輸入數據比例=輸入數據量/總數據量。

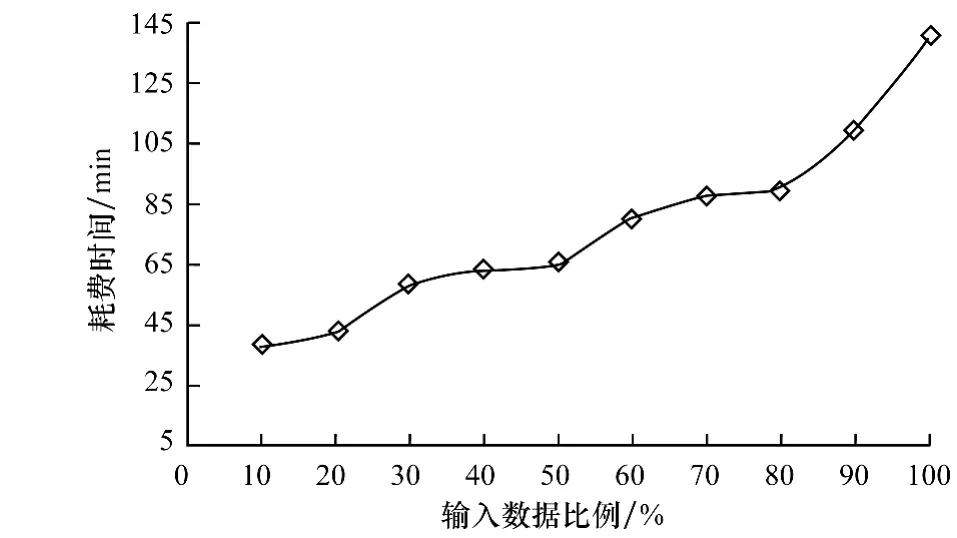
圖6 不同輸入數據量下算法執行時間

實驗結果表明，本文算法在千萬規模的數據集上，未存在計算時間急劇增多的問題，有較強的處理大規模社交網絡的能力。

3．3．2 運行時間隨節點數目的變化

將集群機器的數目改變，觀察算法運行時間與機器數量的關系。

從圖7可以看出，隨著機器數目的增加，算法的運行時間相應減少，這證明算法有很強的可擴展性。從上面的分析中可以看出，本文算法無論是在算法效率還是所得社區模塊度上都要明顯好于基準算法的效果，原因在于本文在第一步迭代信任度的過程中，加強了不直接相鄰節點相互關聯的潛在信息，避免直接進行社區擴散時可能導致的局部最優問題，取得了較好的結果。

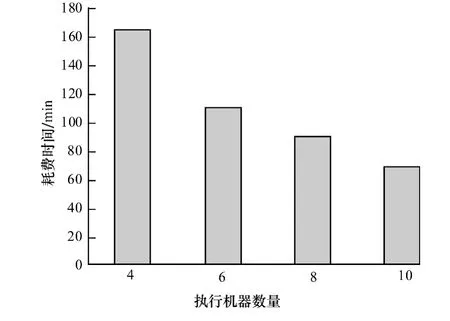
圖7 不同執行機器數目下算法執行時間

4 結束語

本文設計并實現了一種并行化的社區發現算法。該算法首先參考PGP算法里的推薦者信任模型，提出一種根據鏈接關系計算用戶之間信任度的方法，并在此基礎上，進行社區擴散，將處在社交網絡潛在社區內中心位置、與周圍信任度都較高的節點的社區ID傳播到整個潛在社區中，得到社區劃分的結果。本文還利用了Hadoop集群對算法進行并行化設計，使得算法具有較好的可擴展性。在數據集上的實驗結果表明，本文算法既在準確度上有所提高，也有處理大規模社交網絡的能力。然而，在真實的社交網絡中，可能還存在著重疊部分，本文的算法無法適用于社區重疊的情況，需要作進一步的改善。

［1］ Jennifer G，James H．Inferring Binary Trust Relationships in Web Based Social Networks［J］．ACM Transactions on Internet Technology，2006，6(4):497-529．

［2］ Symeonidis P，Ntempos D，Manolopoulos Y．Locationbased Social Networks［M］//Symeonidis P，Ntempos D，Manolopallos Y．Recommender Systems for Location-based Social Networks．New York，USA:Springer，2014:35-48．

［3］ Zimmermann P．Pretty Good Privacy User’s Guide［Z］．1993．

［4］ Jiang W，Wu J，Wang G．RATE:Recommendation-aware Trust Evaluation in Online SocialNetworks［C］//Proceedings of the 12th IEEE International Symposium on Network Computing and Applications．Washington D．C．，USA:IEEE Press，2013:149-152．

［5］ Liu G，Wang Y，Orgun M A，et al．Finding the Optimal Social Trust Path for the Selection of Trustworthy Service Providersin Complex SocialNetworks［J］．IEEE Transactions on Services Computing，2013，6(2):152-167．

［6］ 田俊峰，魯玉臻，李 寧．基于推薦的信任鏈管理模型［J］．通信學報，2011，32(10):1-9．

［7］ Buluc A，GilbertJR．ParallelSparse Matrix-matrix Multipli-cation and Indexing:Implementation and Experiments［J］．SIAM Journal on Scientific Computing，2012，34(4):170-191．

［8］ Zhang Jing，Liu Biao，Tang Jie，et al．Social Influence Locality for Modeling Retweeting Behaviors［C］//Proceddings of IJCAI’13．Menlo Park，USA:AAAI Press，2013．

［9］ Fortunato S．Community Detection in Graphs［J］．Physics Reports，2010，486(3):75-174．

［10］ Lusseau D，Newman M E J．Identifying the Role that Animals Play in Their Social Networks［J］．Proceedings of the Royal Society of London Series B-biological Sciences，2004，271(6):477-481．

［11］ 楊 博，劉大有，劉際明，等．復雜網絡聚類方法［J］．軟件學報，2009，20(1):54-66．