新型功率放大器PLTC行為模型及預失真應用

高明明，南敬昌，劉 月

(遼寧工程技術大學電子與信息工程學院，遼寧葫蘆島125105)

1 概述

無線通信正朝著多載波、多電平、寬頻帶和高頻譜效率方向高速發展，但是也伴隨著信號的峰均比不斷增高，這會使得無線系統中最核心的器件功率放大器進入非線性區，功率放大器在這種情況下將產生記憶效應和強非線性，使系統有效帶寬下降，影響功率放大器的附加效率。正交頻分復用(Orthogonal Frequency Division Multiplexing，OFDM)是一種高速率的多載波傳輸技術，利用多個彼此正交的子載波并行傳輸數據，最大程度利用頻譜資源，具有優異的抗噪聲性能和對抗多徑衰落的能力［1-3］，是4G或B3G的關鍵技術之一。但是OFDM當其載波的相位在某一時刻達到一致時，它的峰均比會很高，使得功率放大器非線性效應對OFDM信號的影響十分嚴重，從而產生帶外譜擴展和帶內失真。帶內失真降低系統性能，出現互調分量，帶外譜擴展則導致鄰近信道干擾。因此為了減小系統對信號的峰均比的要求，補償功率放大器的非線性，可以通過功放線性化技術來改善系統總體的優化設計［4-5］。

功率放大器的行為建模是非常重要的，經常作為分析功放性能的第一步，也為數字預失真技術提供必要的模型基礎。對具有記憶效應的非線性功率放大器建立精準的行為模型是現在研究的熱點問題，把建立的功放行為模型應用于預失真器模型，有助于提高預失真系統的性能及線性度，具有重大的理論實踐參考價值。有對于記憶預失真技術的關鍵就是在于描述功放的逆特性而選擇的非線性模型。

有很多功放行為模型被提出，一般有神經網絡模型和Volterra模型。Volterra級數的模型參數數量隨非線性和記憶深度的增加呈指數形式增長，雖然可以很好地描述非線性系統的物理意義，但是模型的復雜性導致系統參數辨識復雜［6］;模型的記憶效應表征精度低，直接影響了預失真器的線性化性能。因此很多Volterra模型的建立并沒有考慮到功放記憶效應的問題。很多文獻提出了簡化的Volterra模型，多項式模型(Model of Polynomial，MP)［7］，一般多項式模型(GeneralModelofPolynomial，GMP)［8］，包 絡 多 項 式 模 型 (Envelope Model of Polynomial，EMP)［9］、正交多項式模型［10］以及一些兩箱模型。這些兩箱模型如Hammerstein模型分裂增強型 Hammerstein模型、PLME模型、增強型Hammerstein模型、雙非線性雙箱模型(TNTB)，以及Winer模型、LMEC模型等。

本文提出一種新型精確簡化的三箱模型PLTC(parallel-LT-TMP-CIMT)，并用于帶有記憶效應的非線性功率放大器行為建模及預失真。該模型由查找表(Look-up Table，LUT)、三角記憶多項式(Triangular Memory Polynomial，TMP)［8］和記憶時刻信號交叉項并聯構成。PLTC模型在行為模型和預失真中的性能是使用16QAM信號驅動一個強非線性大功率Doherty功率放大器來驗證所提模型的性能。同時將新模型的性能與GMP模型、MP模型、PLME模型以及LMEC模型進行全面的比較，即通過對各種模型的NMSE、EPSD，以及系數數量進行的比較。

2 PLTC行為模型描述

PLTC模型是一個三箱模型，由3個非線性子模型并聯而成。由高階無記憶高階非線性函數、低階記憶多項式以及記憶時刻信號交叉項CIMT函數組成，先后處理了強靜態非線性和動態非線性。PLTC模型的結構如圖1所示。PLTC模型通過引入當前信號與其滯后包絡項之間的交叉項，獲得更高的準確度，并通過增加查找表單元來表征靜態強非線性，降低了記憶多項式子模型和包絡記憶多項式子模型中對非線性的階數要求，從而降低了整個模型的復雜度。由于在PLTC模型中，包含了同一時刻信號的交叉項、當前時刻與記憶時刻的交叉項以及記憶時刻信號間的交叉項三部分，因此，更加符合實際功放的非線性特性和記憶效應特性，適用于寬帶功率放大器的建模。

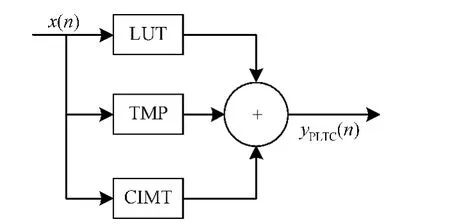
圖1 PLTC模型框圖

第1個子模型采用無記憶高階非線性函數，可以用查找表結構來實現。其數學表達式為:

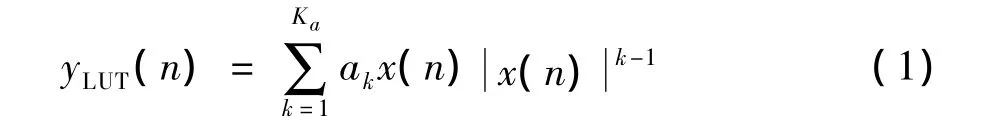
其中，x和y分別為第1個子模型的輸入和輸出信號;Ka表示非線性階數;ak表示第1個子模型的參數。

第2個子模型三角多項式(TMP)函數，描述無線通信系統中功放的非線性可以用離散有限記憶復基帶Volterra級數來表示，定義公式如下:

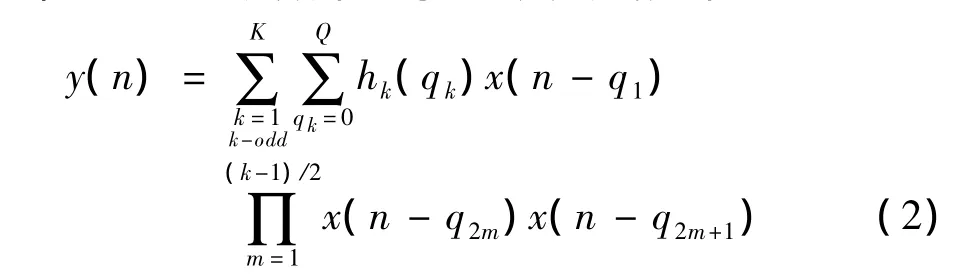
其中，x(n)和y(n)為系統的輸入和輸出;K為非線性階數;Qk為記憶深度;hk(qk)為k階Volterra核;qk由整數值延遲組成;對所有的 k=1，3，…，K有qk=0，1，…，Qk。龐大的系數數量使得 Volterra級數難以在實際中得到應用，因此在實際建模和DPD中常采用簡化的Volterra級數模型。

多項式模型(MP)為簡化了的Volterra級數模型。其輸入x(n)，輸出y(n)可表示為:

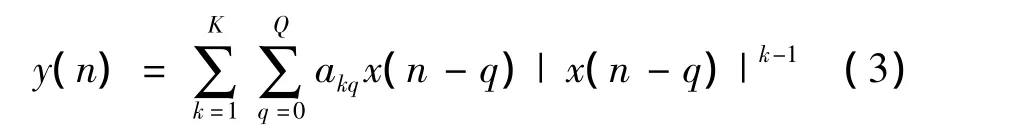
其中，k是非線性階數;q是記憶深度;x(n)和y(n)分別為多項式的輸入信號和輸出信號。在式(1)中，x(n－q)的k階多項式表征，akq為MP模型系數。最大非線性階數對輸入來說一般是恒定的。在基于OFDM無線寬帶通信系統中，當長期記憶效應被考慮進來的時候，最大記憶階數會比較大，這導致了大量系數的產生并提高了計算的復雜性。但由于在實際的實踐觀察中得知非線性動態效應會隨著記憶階數增加而逐漸減小，因此可以試著調整過去輸入的最大非線性階數在保持功放預失真性能的同時降低其系數數量。K=N，N定義如下:

那么式(3)變成:

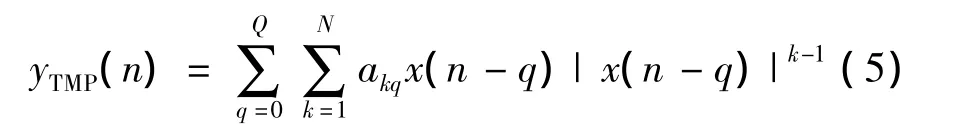
N為最大非線性階數時，Q是最大記憶深度。在式(4)中，最大非線性階數N是不連續的，是隨著記憶深度而變化的。把式(5)稱為TMP模型。在TMP模型中是Volterra模型的一種簡化形式，它只考慮Volterra核函數中對角線的值，其他均忽略不計，這樣模型中系數會隨記憶深度和非線性階數呈指數增長的問題就會被很好地解決［6］，可以使得系統隨非線性階數和記憶深度呈線性增長的關系［8］。

考慮到PLTC模型中查找表(LUT)表征了靜態非線性，因此TMP模型不包括無記憶項，q從1開始取值。TMP增加了歷史時刻包絡對當前輸入信號的影響項。

第3個子模型采用記憶時刻信號交叉項CIMT函數表示，其數學表達式為:

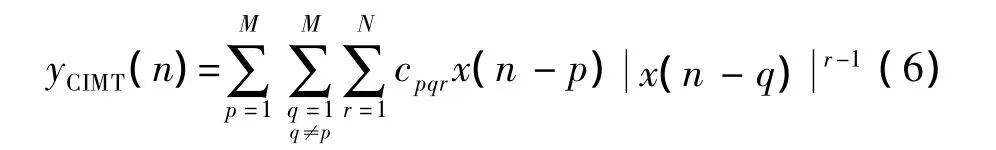
其中，CIMT子模型的輸出和輸入信號分別用y和x表示;CIMT子模型的交叉項的階數和交叉記憶深度分別用N和M表示;cpqr為CIMT模型的系數。記憶時刻的信號之間的高階非線性項對系統的影響較小，而且在模型各項中，階數增加會導致模型系數量的快速增長，大大增大了復雜性，所以本模型只考慮記憶時刻信號間的三階交調量，對系統影響較大的令式(3)中的r=3，式(3)化簡為:

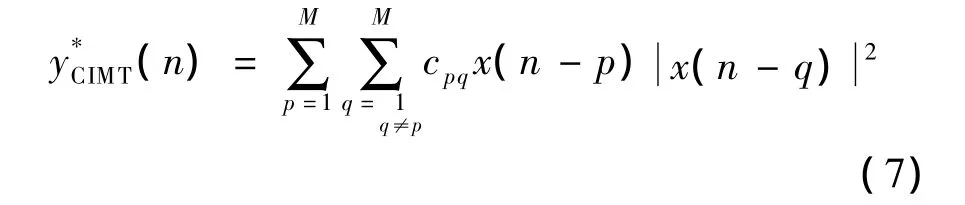
將式(1)、式(6)和式(7)相加，構成了新型PLTC模型，PLTC模型的數學表達式為:

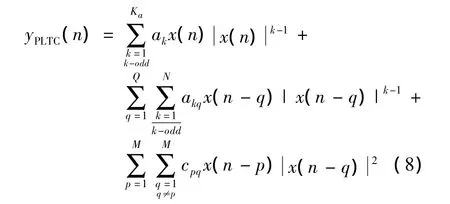
此模型避免了串聯形式下每個子模型需要同時選擇同樣非線性階數的問題，各項非線性階數相同會導致模型尺寸太大而增加模型計算的復雜度，因此PLTC模型需要通過一些方法來減小模型尺寸，通過添加并聯非線性子模型來解決。LT項表征了功率放大器的高階靜態非線性行為，TMP的子模型表征了功率放大器的低階非線性并控制了模型的尺寸，使總系數個數變得合理［11-14］。TMP增加了歷史時刻包絡對當前輸入信號的影響項。CIMT函數增加了記憶時刻信號交叉項。

3 PLTC模型的辨識

PLTC模型中LT，TMP和CIMT子模型可以彼此獨立地設置其非線性階數和記憶深度來提升整體模型的性能，如果按照習慣的方法會同時對這些子模型的記憶深度和非線性參數進行掃描，這樣就會得到大量不合理的組合，并增加了計算量。因此，必須采取分步的方法進行系數的確定。這樣既能提高模型的性能，又使得計算復雜度沒有明顯的增加。

PLTC模型的辨識分為3步。首先利用被測功放的輸入輸出數據完成無記憶高階靜態非線性子模塊的參數辨識，其次將功放的輸入輸出數據向下嵌入到TMP子模型中進行參數識別，最后對CIMT子模型中參數完成識別。

TMP子模型與CIMT子模型可同步辨識，首先令:

其中，Y是2個動態非線性多項式子模型的輸出向量;X為基于2個多項式基函數與輸入信號構成的矩陣。A是包含了TMP子模型與CIMT子模型系數的向量。矩陣X被定義為:

其中，XTMP和XCIMT分別為TMP與CIMT基函數構造的子矩陣。

其中，j以掃描方式從0～MCIMT;i以掃描方式從0到NCIMT。

最后，用最小二乘法法進行擬合，求得A為:

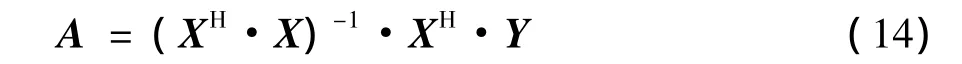
其中，［·］H為共軛轉置。

是否能增強模型的整體性能和選取適當的模型系數是PLTC模型的子模型尺寸的選取所要權衡的兩方面。模型精確度用歸一化均方誤差(Normalized Mean Square Error，NMSE)指標來衡量。模型尺寸一般選取能得到更小的歸一化均方誤差值以及對應組合產生系數最少的值。子模型尺寸的確定用一般的掃描方法。

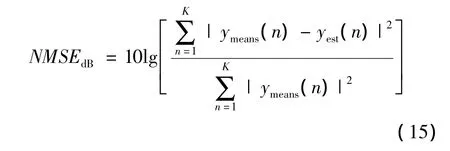
其中，ymeans為實際測量的功放輸出波形;yest為模型的輸出波形;K是輸出波形樣本的數量。

首先完成無記憶高階靜態非線性子模塊的參數辨識，對LT的非線性階數進行掃描，從1～17。然后，TMP子模型參數的確定是用足夠大范圍的掃描模型同時對TMP子模型的非線性階數和記憶深度進行掃描的。記憶深度掃描從0～5，非線性階數從0～15。TMP子模型中最大非線性階數是不連續的，是隨著記憶深度而變化的，忽略偶次項就克服了傳統最大記憶階數會比較大而導致的大量系數的產生并提高了計算復雜性的問題。

TMP模型的參數被確定時，CIMT子模型也在第三步被確定，CIMT子模型參數也同時在足夠大范圍掃描。對應每次迭代，TMP子模型和CIMT子模型系數同時確定，如同式(9)～式(14)描述。子模型的準確性是使用NMSE量化的指標，最后子模型參數選擇產生系數最少，達到最低NMSE的對應組合。

在分別對各個子模型進行系數選取時，有時可以獲得最佳NMSE值的組合會使系數數量變得很高，因此，非線性階數和記憶深度組合的選取要兼顧計算量的復雜性以及模型的精確度，要從中選取一個合適的方案。

最后確定LT的非線性階數為11，TMP子模型的記憶深度和非線性階數分別為7和5，忽略偶次項。CIMT子模型的記憶深度為3。PLTC模型的總系數個數是25，模型的NMSE值為－37．22 dB。

4 模型性能評估及驗證

為了驗證PLTC模型的性能，利用矢量信號發生器(N5182A)、高功率 LDMOS Doherty功率放大器、頻譜分析儀(PXA N9030A)、衰減器搭建測試平臺，如圖2所示。采用16QAM信號作為輸入信號。被測功放的中心頻率是 1．96 GHz，增益為50 dB。

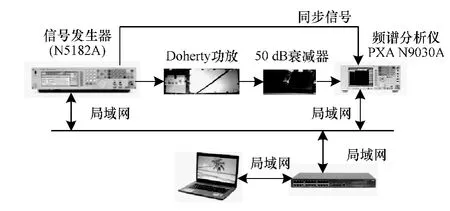
圖2 實際測試平臺

PLTC模型由于Ka，K，Q和M值的選擇直接影響模型的精確度，對這4個參數同時進行掃描會得到大量不合理的組合，提升了計算量，因此首先估計無記憶非線性子模型LT的參數Ka。利用采集到的數據建立無記憶非線性模型，非線性階數從1掃描到17，圖3顯示了對應不同Ka值時的NMSE。從圖3可以看出，隨著非線性階數的增加，模型的精確度也隨之升高，但同時伴隨著系數的增加。為兼顧模型精確度和復雜度兩方面因素，選擇Ka=11作為無記憶非線性子模型的參數。

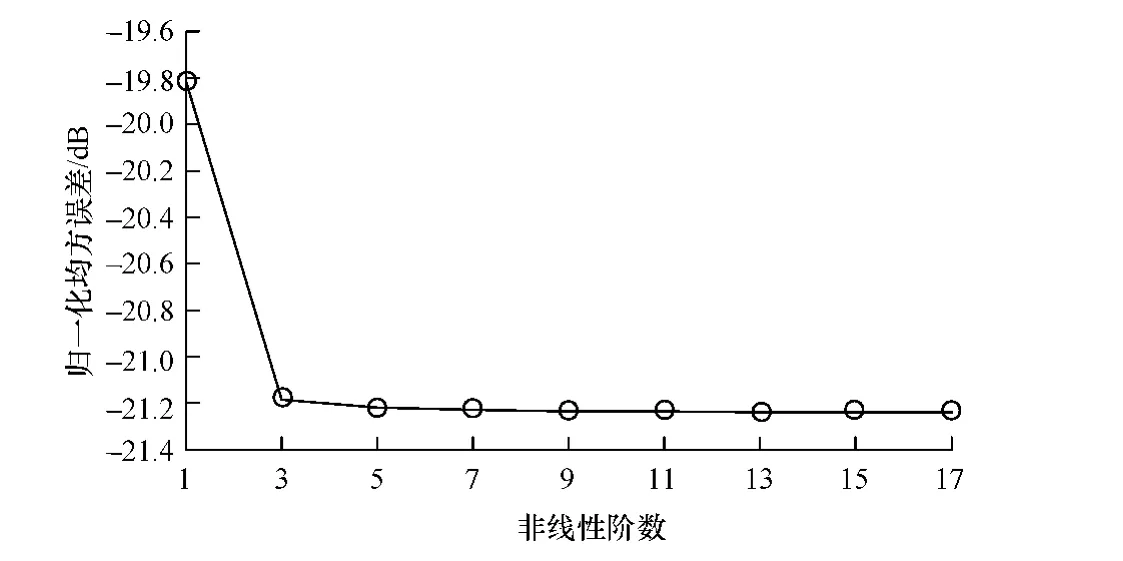
圖3 歸一化均方誤差性能曲線

射頻功率放大器中帶有記憶效應的輸入分量階數越高，對輸出的影響越小，記憶效應隨著時間變長而減弱，因此TMP子模型的非線性階數K可以適當降低，選取合理的值。對非線性階數從0掃描到15，記憶深度Q從0掃描到5。在時域中，功放模型的精確程度用歸一化均方誤差(Normalized Mean Square Error，NMSE)指標來衡量［15］。圖4 利用三維立體圖展示了對應不同K和Q值時的NMSE值，K=11時，NMSE為–21．236 2。從圖4中可以看到，隨著模型非線性階數與記憶深度的增加，文中所建立模型的精度逐漸提高。對射頻功率放大器進行建模時，必須合理地選取非線性階數K和記憶深度Q，結合較少的系數與較小的NMSE值綜合決定系數的取值。非線性階數和記憶深度的增加會使模型的準確度得以提升，但模型系數的數量也大大增加了。因此，TMP模型選取K=7，Q=5。忽略偶次項，大幅降低了模型的復雜性。為進一步降低PLTC模型的復雜度，令CIMT子模型中的M=3。

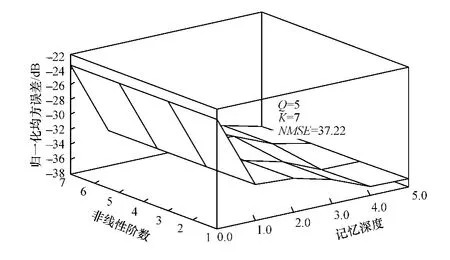
圖4 歸一化均方誤差性能三維立體圖

PLTC模型最終選定LT子模型的非線性階數為11，TMP子模型的記憶深度和非線性階數分別為7，5，CIMT子模型的記憶深度為3。其中，LT子模型系數為11，TMP模型的參數為K=7，Q=5，忽略偶次項，共8個系數，CIMT子模型系數為6。合計共25個參數。因此，PLTC模型的總系數個數是25，模型的 NMSE值為 －37．22 dB。表1為 PLTC模型與多項式模型 MP、一般多項式模型 GMP、LMEC模型的總系數與NMSE的對比。

表1 不同模型NMSE與總系數比較

圖5為利用LPTC模型作為預失真器對功放進行數字預失真前后的輸入輸出幅度特性曲線。可以看出，經數字預失真后的輸入輸出幅度特性曲線得到顯著改善，基本上形成一條直線，可以滿足系統要求。

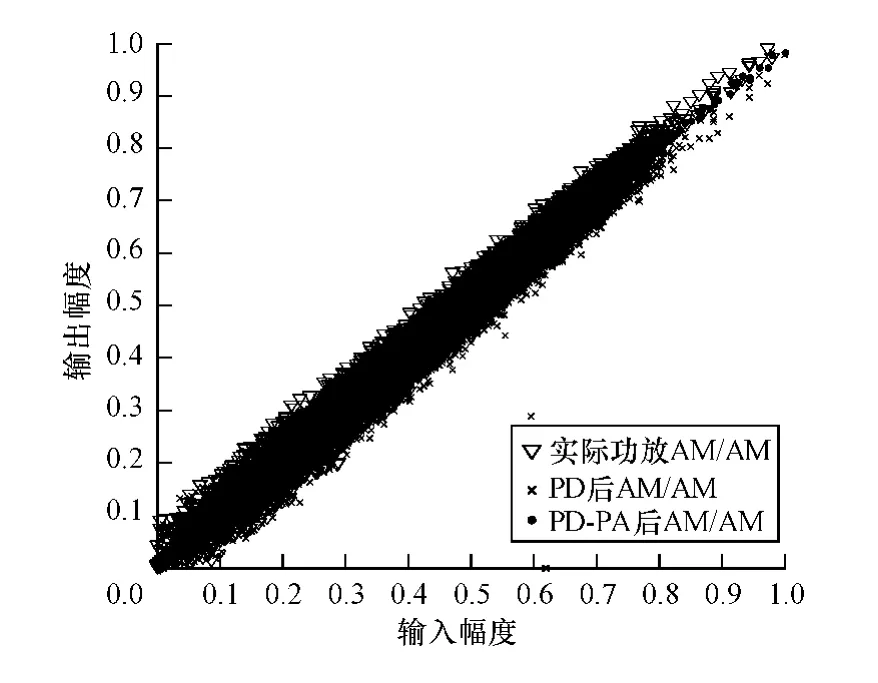
圖5 輸入輸出幅度特性曲線

在數字預失真技術中，所使用功率放大器行為模型的準確度越高，則仿真可以得到的預失真效果就越接近實際中的情況，將PLTC模型應用到數字預失真系統中，同時與MP模型、GMP模型和LMEC模型的預失真性能進行比較。圖6為使用16QAM信號時，使用3種模型進行數字預失真前后的功率譜密度。

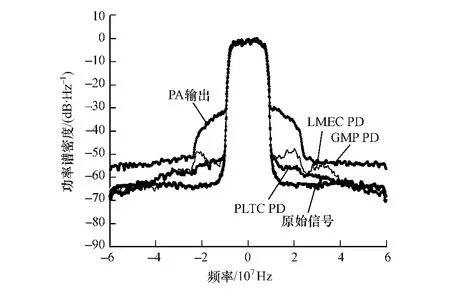
圖6 3種預失真方法性能比較

利用實際測試平臺來驗證PLTC預失真方法的實際線性化效果。對原始的輸入信號采用PLTC方法構建預失真器，數字預失真前后功率放大器輸出信號的PLTC對比如圖7和圖8所示，可以看出，經過PLTC預失真方法后，ACPR有大約22 dB的改善，說明該方法能夠有效地對功放進行線性化。

圖7 無預失真時功放輸出信號的ACPR值

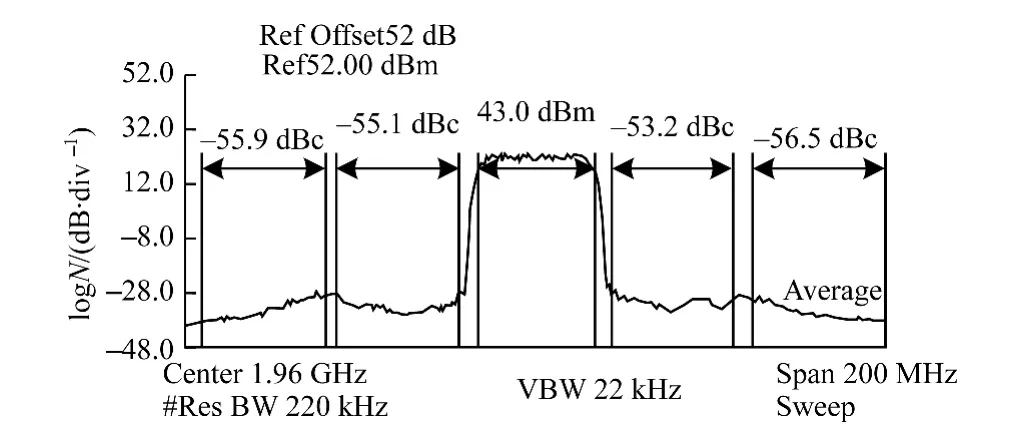
圖8 有預失真時功放輸出信號的ACPR值

5 結束語

本文針對功率放大器的記憶效應和非線性特征提出了PLTC模型。PLTC模型用于功率放大器的行為模型建模以及數字預失真的應用，該模型是簡化的三箱模型，由查找表、三角記憶多項式和記憶時刻信號交叉項并聯構成。使用16QAM信號驅動一個強非線性大功率Doherty功率放大器來驗證所提模型的性能。實驗結果表明，與 MP模型相比，PLTC模型的NMSE改善了3．02 dB，系數量節省了65%;與 GMP模型相比，PLTC模型的 NMSE與GMP和LMEC模型的NMSE相差不大，但是其系數量大大降低，比 GMP模型系數節省了75%;比LMEC模型系數節省了50%。對原始的輸入信號采用PLTC方法構建預失真器，經過PLTC預失真方法后，ACPR有大約22 dB的改善，說明該方法能夠有效地對功放進行線性化。

［1］ Kwan A，Hammi O，Helaoue M，et al．High Performance Wideband DigitalPredistortion Platform for 3G +Applications with Better than 55dBc over 40 MHz Bandwidth［C］//Proceedings of IEEE MTT-S International Microwave Symposium．Piscataway，SA:IEEE Press，2010:1082-1085．

［2］ Roblin P，Keun S，Chaillot D M，et al．Frequencyselective Predistortion Linearization of RF Power Amplifiers［J］．IEEE Transactions on Microwave Theory and Techniques，2008，56(1):65-76．

［3］ Sung C J，Hammi O， Ghannouchi F M． Design Optimization and DPD Linearization of GaN-based nsymmetrical Doherty Power Amplifiers for 3Gmulticarrier Applications［J］．IEEE Transactions on Microwave Theory and Techniques，2009，57(9):2105-2113．

［4］ 吳 靜．OFDM系統中的預失真技術研究［D］．西安:西安電子科技大學，2008．

［5］ 李 波．無線通信中射頻功率放大器預失真技術研究［D］．西安:西安電子科技大學，2009．

［6］ 廖 意，蘇東林，吳 琦，等．基于Volterra級數的功放行為模型建模與簡化［J］．北京航空航天大學學報，2013，39(7):990-994．

［7］ Hammi O，Ghannouchi F M，Vassilakis B．A Compact Envelope Memory PolynomialforRF Transmitters Modeling with Application to Baseband and RF-digital Predistortion［J］．IEEE Microwave and Wireless Components Letters，2008，18(5):359-361．

［8］ Yu Cuiping，Liu Yuan’an，Du Tianjiao，et al．New Predistorter sing Triangular Memory Polynomial for Power Amplifier of OFDM-based Wireless Broadband Communication System［J］．The Journal of China niversities of Posts and Telecommunications，2012，19(2):43-47．

［9］ Morgan D R，Ma Zhengxiang，Kim J，et al．A Generalized Memory Polynomial Model for Digital Predistortion of RF Power Amplifiers［J］．IEEE Transactionson Signal Processing，2006，54(10):3852-3860．

［10］ 佀秀杰，金明錄．一種新的用于Hammerstein預失真器的自適應結構［J］．電子與信息學報，2011，33(6):1345-1349．

［11］ Younes M，Hammi O．An Accurate Complexity-reduced“PLME”Model for Behavioral Modeling and Digital Predistortion ofRF PowerAmplifiers［J］．IEEE Transactions on Industrial Electronics，2011，58(4):1397-1405．

［12］ 曹新容，黃聯芬，趙毅峰．一種基于Hammerstein模型的數字預失真算法［J］．廈門大學學報:自然科學版，2009，48(1):47-50．

［13］ Hammi O，Ghannouchi F M．Twin Nonlinear Two-box Models for Power Amplifiers and Transmitters Exhibiting Memory Effects with Application to Digital Predistortion［J］．IEEE Microwave and Wireless Components Letters，2009，19(8):530-532．

［14］ Ding Lei，Morgan D R，Ma Zhengxiang，et al．A Robust Digital Baseband Predistorter Constructed sing Memory Polynomials［J］．IEEE Transactions on Communications，2004，52(1):159-165．

［15］ 金 哲，宋執環，何加銘．基于簡化Volterra級數的射頻功率放大器建模與辨識［J］．電路與系統學報，2008，13(5):90-94．