HTS電動機定子開槽引起的轉子渦流損耗計算
譚登洪,鄭 軍
(武漢電力推進裝置研究所,武漢430064)
0 引言
高溫超導(HTS)電機與傳統電機相比具有體積小、重量輕、噪音低、效率高、制造成本低、營運成本低和維修較少等優點;此外,電機在運行中負荷作寬范圍變化時,其高效率基本維持不變[1-4]。因此,HTS電機的研究對國防裝備和國民經濟建設都具有十分重要的意義。
HTS電機定子通常采用氣隙(無槽)電樞結構形式,對于初次進行HTS電機研究的項目,基于項目研究目的、研究經費和進度的考慮,也可采用常規電樞形式,盡管這樣與大容量電機的結構有一定差異,但可以集中精力解決轉子低溫電氣工程方面的問題,同時也可起到減少超導帶材用量的作用。
但HTS電機采用常規電樞結構形式時,定子開槽將帶來氣隙寬度的不均勻變化,從而產生了定子齒諧波。齒諧波和其它高次諧波一方面增大超導勵磁區域垂直磁場,進而降低臨界勵磁電流的大小,對提高氣隙磁密不利;另一更重要方面,齒諧波和其它高次諧波將會在轉子結構件中產生渦流,這些損耗過大將引起HTS帶失超,嚴重時將使HTS帶熔融毀壞。為消除這些不良影響,通常采取在外轉子加一個電磁阻尼屏來屏蔽這些諧波。另外,電磁阻尼屏還可消除負序及不對稱的故障電流所產生的相對轉子 2倍額定頻率的磁場,和由故障電流所產生的跳躍變化[3],因此需要對電磁阻尼屏的屏蔽效果進行精確的計算。
常用的電磁阻尼屏主要有圖1所示的兩種形式,支撐層由反磁性不銹鋼制成,電磁屏由高純銅制成。這兩種轉子電磁電磁阻尼屏蔽僅在結構上有區別,在屏蔽和阻尼效果上沒有不同之處,夾心式機械強度更好,但制造也要麻煩些。另外,Lawrenson(1976年)等人建議采用一種不同質有孔的屏蔽系統。

本文以某HTS電機為例,推導了HTS電機電磁場數學模型,采用場路耦合時步有限元法對齒諧波以及電樞反應引起的高次諧波在轉子結構件中產生的渦流損耗進行計算,計算了定子槽數和槽形對渦流損耗的影響,分析了電磁阻尼屏厚度與磁屏蔽效果的關系,同時計算了磁性槽楔對轉子結構件渦流損耗的影響。
1 HTS電機數學模型建立有限元與分析
某HTS電機二維結構模型如圖2所示,其運行原理和普通凸極同步電機類似。其轉子與普通電機轉子不同,主要由內外轉子構成。其中外轉子(電磁阻尼屏)由支撐殼和電磁屏構成,電磁屏主要起磁屏蔽作用,支撐殼主要起支撐作用,也有一定的磁屏蔽作用;內轉子主要由勵磁繞組、轉子骨架和轉子鐵心構成,其中轉子鐵心主要起改善勵磁繞組受力和提高氣隙磁密等作用。這些轉子結構件特別是內轉子結構件的渦流損耗將對HTS勵磁繞組正常勵磁和電機的安全運行產生很大的影響。
因此,電磁阻尼屏蔽系統的設計必須保證在內轉子結構件中產生的渦流損耗很微小或沒有,以及超導線中的磁通變化不會使超導體失超。
為便于計算,分析時作下述假定:
1)磁場沿軸向不變,電機內磁場作二維場處理;2)定子磁屏蔽外表面沒有漏磁,即磁力線平行于定子磁屏蔽外圓;3)定子磁屏蔽鐵心磁導率各向同性。

根據對稱情況,選擇圖2中電機一個極作為求解區域,在求解區域內矢量磁位A滿足電磁方程[5]

下面分別就求解域中的各個區域進行分析。
1)定子鐵芯、氣隙和轉子非勵磁電流區域
忽略鐵芯中的渦流效應,在鐵芯和氣隙中J=0,對式(1)進行單元分析后,得到具有如下形式的矩陣方程

2)定子繞組區域
不考慮定子繞組中的渦流效應中,得定子電路方程如下:
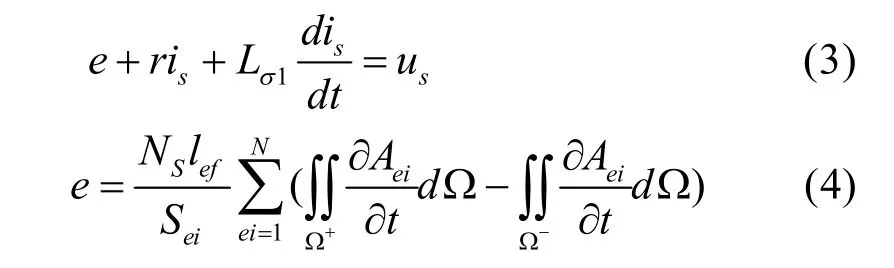
把式(4)代入(3)得

式中,r—每支路繞組的電阻;Lσ1—支路繞組的端部漏感Sei—單元面積;Aei—該單元中磁動勢的平均值;Ns—定子每個支路繞組中的串聯導體數。將矢量磁位和電流對時間的導數用差分來代替,經過整理,得定子繞組區域的矩陣方程:
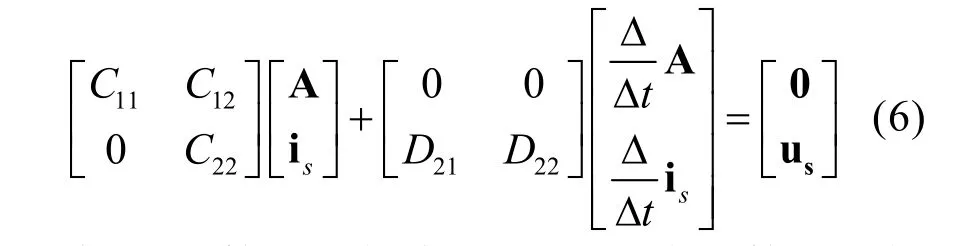
式(6)第一行與式(1)相對應,第二行與式(5)相對應,C11、C12、D21、D22分別由對應的系數項經單元合成而得。
3)勵磁繞組區域
勵磁繞組為超導磁體,無電阻,僅有直流電流if,因此有

4)總體合成方程
由以上分析,可以得到整個電機的場路耦合方程為

對上式進行時步有限元求解在時步法中,可用有限元復數模型來確定初值A(0),I(0)。因為鐵磁材料的磁導率具有非線性的特性,式(8)用牛頓——拉夫遜法求解,在每一步迭代中用不完全喬利斯基分解——共軛斜量法求解線性方程組。
2 轉子結構件渦流計算
轉子電磁屏蔽及其他結構件的渦流電流主要取決于定子齒諧波的大小,并且定子繞組正弦分布,因此轉子表面的矢量磁勢的空間分布可謂表示為[6]
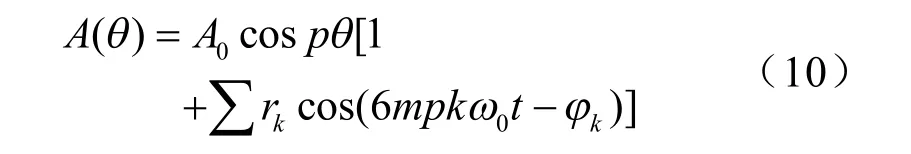
因此渦流電密可得到

由上式看出,產生的渦流是矢量磁勢A0的系數值的函數,A0和rk與電機負載狀況和導磁材料有關。
3 計算結果與分析
3.1 電機參數
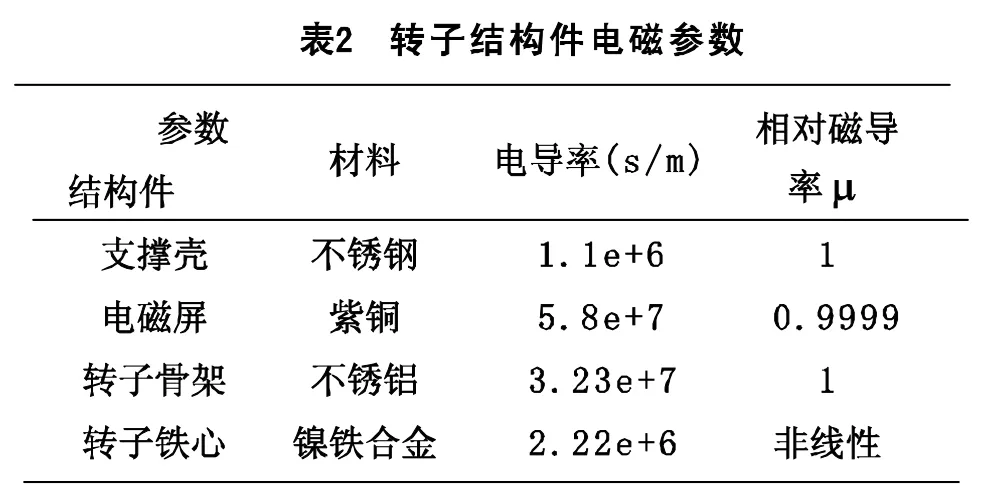
某HTS電機主要結構和材料參數如表1和表2所示,選用圖1(a)的電磁屏蔽結構形式。由于電磁屏的導電率越高厚度越厚其屏蔽作用越強,因此電磁屏也選用高純銅。計算時,考慮到渦流電流是矢量磁位對時間的導數,所以時間步長取得越短計算結果越準確,這里時間步取為0.00001 s。

?
?
3.2 定子槽形結構對轉子結構件渦流損耗的影響
3.2.1 槽數的影響
取電磁屏蔽厚度均為6 mm,計算定子54槽和72槽時轉子結構件渦流損耗,計算時54槽額定勵磁電流為60 A,定子電流89.2 A,72槽額定勵磁電流為58 A,定子電流88.86 A。

?

算得額定負載時考慮轉子渦流損耗的磁場分布如圖4所示,渦流損耗值如表3所示,從中看出采用 72槽轉子電磁屏蔽及內轉子結構件渦流損耗大大減小,這由于采用72槽時,定子槽形變小,減小定子齒諧波的強度及其投入深度。所以該電機選用72槽。
3.2.2 槽形及槽楔性能的影響
取定子72槽,電磁屏厚度為6 mm,根據式(11)算得不同槽形(圖5)和槽楔材料時轉子結構件渦流損耗如表4所示,其中磁性槽楔相對磁導率為10。
由表4看出:
1)定子槽形采用半開口槽時較之采用全開口槽,轉子結構件渦流損耗較小,特別是非磁性槽楔時效果更為明顯,渦流損耗減少了29.5%;
2)較之采用非磁性槽楔當采用磁性槽楔,轉子結構件渦流損耗明顯減小,全開口槽和半開口槽分別減少57.6%和44.3%。這是由于槽口寬較窄的半開口矩形槽和磁性槽楔,均能夠有效地降低定子齒諧波強度,進而減小轉子結構件渦流損耗。

3.3 外轉子電磁屏蔽厚度的確定
這里在定子72槽,槽形為全開口槽,采用非磁性槽楔的情況下,以內轉子結構件渦流損耗較小為設計目標,確定外轉子電磁屏厚度。
根據式(11)算得電磁屏蔽厚度hcu分別為4 mm、6 mm和8 mm時,轉子結構件渦流損耗如表5所示。

?
從圖6和表5看出:1)電磁屏越厚,內轉子結構件渦流損耗越小;2)電磁屏厚度達到一定大小后,屏蔽效果提高很小,如hcu=6 cm或8cm時的各項渦流損耗基本相等,但二者較hcu=4 cm時內轉子結構件渦流損耗減小了56.72%,已很微小。這是因為hcu=4 cm時齒諧波投入電機內轉子在超導勵磁線圈中將感應出較大的渦流損耗,而hcu=6 cm與hcu=8 cm兩種情況下,定子齒諧波已基本被外轉子的電磁屏蔽銅環屏蔽,不會透入到內轉子中去,或即使透入也很弱。圖7為hcu=6 cm時各結構件瞬時電密分布。

根據以上計算,對樣機,定子采用72槽,磁性槽楔,槽楔厚度為 4 mm,考慮到轉子內空間結構的大小,取電磁屏厚度為 6 mm,算得轉子結構件渦流損耗總和為80 W。
4 結論
通過以上對定子開槽的HTS電機轉子結構件渦流損耗的分析計算,得出如下結論:
1)定子槽口寬越小,由定子開槽引起的齒諧波強度越弱,對轉子結構件渦流損耗越小,因此設計時應在下線工藝允許的范圍內,盡量減小定子槽口寬;2)定子采用一定相對磁導率的磁性槽楔,可有效的減小齒諧波的影響,設計時應兼顧齒諧波的減小和漏磁增加兩方面考慮,來確定磁性槽楔厚度,對本文計算樣機磁性槽楔取其極限厚度4 mm為宜;3)電磁屏厚度一定時,選用電導率越高的非導磁材料屏蔽效果越好;電磁屏材料一定時,其厚度越大屏蔽效果越好,但達到一定厚度后,電磁屏厚度再增加,所起到的屏蔽效果提高很小,設計時需綜合考慮屏蔽效果和轉子內空間大小而確定電磁屏厚度。

[1]Biao,Gu Guobiao,Zhang Guoqiang,et al.Analysis and design of cooling system in high temperature superconducting synchronous machines [J].IEEE Transaction on Applied Superconductivity,2003,17(2): 1577-1560.
[2]MICHAEL Frank,PETER Van Habelt,PETER Kummeth.High-temperature superconducting rotating machines for ship applications[J].IEEE Transaction On Applied Superconductivity,2006,16(2): 1465-1468.
[3]SWARM S.Kalsi.Development status of rotating machines employing superconducting field windings[J].Proceedings of The IEEE,2004,92(10):1688-1704.
[4]SWARM S.Kalsi.Development status of superconducting rotating machines[J].IEEE PES Meeting,New York,2002: 27-31.
[5]VASSENT E,MEUNIER G,SABONNADIERE J C.Simulation of induction machine operation using complex magnet-dynamic finite elements[J].IEEE Trans on Mag,1989,25(4): 12-14.
[6]FREDERIC Bouillault and ADEL Razek.Eddy currents due to stator teeth in synchronous machine rotors[J].IEEE Trans on Mag,1984,20(5):1939-1984.

