基于改進型粒子群算法的艦船消磁電流調整方法研究

夏建超，徐正喜，左 超，耿 攀

（武漢第二船舶設計研究所，武漢 430205）

0 引言

現代艦船大都由鋼鐵材料建造，在地球磁場作用下會產生感應磁場，造成空間磁場畸變，成為暴露并破壞艦船隱身性能的重要物理特征。加裝消磁系統是提升艦船磁隱身性能的重要手段，而消磁繞組電流的調整是影響消磁系統補償性能的關鍵[1]。

求解艦船消磁繞組的電流等效于解一個多元一次矛盾方程組，由于該方程組沒有確定的解析解，因此通常采用最優解算法比如最小二乘誤差（LMS）算法對其進行擬合，然而這種方法主要是減小艦船結果磁場特征的均方根（RMS）誤差，它不以求解磁場峰值最小（PM）為目的。

而根據現代艦船磁隱身技術的要求，降低艦船空間結果磁場峰值成為最主要的目標[2]。針對這一目標，本文提出了目標函數為磁場峰值最小的粒子群算法，迭代求解每一個粒子的適應值，最終得到消磁繞組通電電流的最優解。同時為了使該粒子群算法快速收斂，又不至于陷入局部最優，本文通過最小二乘法初步約束粒子位置和速度的范圍，對其進行了改進。算例的實施和對比表明，這種改進型粒子群算法具備收斂速度快、優化結果穩定等優點。

1 艦船消磁原理

對采用分區消磁技術的艦船消磁系統，每個消磁繞組電流可單獨進行控制，以縱向消磁繞組為例，典型的船舶消磁系統如圖1。

首先，測量艦船在地磁場激勵下、典型測量線上的磁感應強度。然后，在無外界磁場激勵條件下，分別對每一個繞組通以單位安培電流，在相同的測量線上測量磁感應強度數值，作為該繞組的效率。最后，通過調整各繞組電流，使繞組的疊加磁場與艦船感應磁場盡可能大小相等、方向相反，以達到消磁目的。假設測量線上有m個點，縱向繞組共有n組，第i個區段的安匝量為xi，當安匝量為1時在第j個測量點上產生的磁場為aj,i，而這第j個測量點上的艦船感應磁場為bj；當j從1取到m時，得如下方程組

其中bj，aj,i可通過測量得到，方程組左邊系數構成繞組效率矩陣A，右邊為艦船感應磁場矩陣B，需要確定繞組安匝量矩陣 X，使 AX-B的峰值最小（PM），即可達到較好的消磁效果[3]。

2 算法介紹

2.1 最小二乘法原理

最小二乘法可使上述方程AX-B誤差平方和最小，也就是使方程組中每個方程左右兩端之差

的平方和取極小值，即

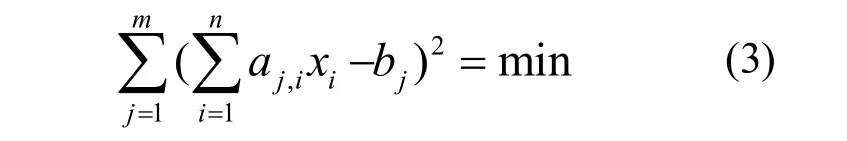
對其求偏導，有

其中k＝1,2,…n，若令，，則該方程可用下列矩陣表示

其中，C＝ATA,D＝ATB，該方程組的解是確定和易求的[4]。

2.2 粒子群算法原理

粒子群優化算法采用群體與進化的概念，將個體看作是在n維搜索空間中的一個沒有重量和體積的粒子。首先，在解空間內隨機初始化粒子，這些“粒子”在解空間內以某種規律移動，經過若干次的迭代后找到最優解。每一次迭代中，粒子通過跟蹤兩個值來更新自己：一個是粒子本身的最優解（pbest），另一個值是整個粒子群體當前找到的全局最優解（gbest）。找到這兩個值后，每個粒子根據自己的飛行速度，決定自身的走向及飛行距離而不斷進化。上述過程可由進化方程描述為：

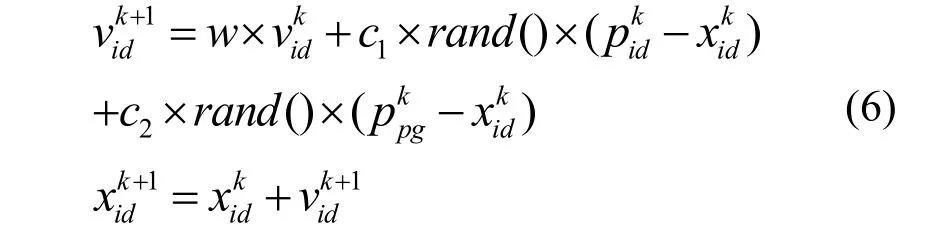
其中w表示慣性權重，i表示第i個粒子，d表示粒子的第d維，k表示第k代，rand()產生［0，1］的隨機數，c1、c2表示加速常數[5]。

粒子的位置范圍對算法的收斂能力起著重要的作用，合適的粒子位置范圍有利于解的快速收斂。粒子的飛行速度有一個最大值vmax，用來限制粒子飛行速度。vmax決定了粒子在解空間的搜索精度，如果vmax太大，粒子會飛過最優解；如果太小，粒子則陷入局部最優解而無法進行全局搜索。因此，通過調整粒子位置、粒子飛行速度可以達到粒子群算法的最佳尋優能力[6]。

2.3 改進型粒子群算法

對進化算法的研究表明，如果能壓縮搜索空間，就可以提高優化算法得到最優解的幾率[6]。而在以結果磁場峰值最小為目的使用粒子群算法求解消磁電流之前，難以確定每個繞組的電流范圍，也難以確定粒子的飛行速度。而以結果磁場方差和最小為目的的最小二乘法卻能快速準確的得到每個繞組的電流值。由于兩者解的相似性，可將最小二乘法得出的繞組電流范圍應用于粒子群算法的程序中，此時粒子飛行速度也會有一個參考，最優解也必須至少小于最小二乘法求出的最小峰值才有價值。

3 算法在艦船消磁電流調整中的應用

如圖1所示的某艦船在只有縱向地磁場激勵下，在某測量線101個點上的磁感應強度曲線構成感應磁場矩陣B，如圖2。

在該船上設置10個縱向消磁繞組，分別單獨通電1安培的效率曲線如圖3，測量線上的各繞組通電產生的磁場構成繞組效率矩陣A。

如2.1節所述，由最小二乘法可求解繞組電流矩陣IRMS，在 matlab中，可使用命令IRMS＝pinv(A)*B快速得到，將補償磁場D1＝A*IRMS的曲線與感應磁場 B的曲線進行比較，感應磁場與補償磁場差值即消磁之后的結果磁場為E1=D1-B，如圖4所示。

以上最小二乘法求解得到繞組電流值矩陣：

以此作為粒子群算法中粒子位置和速度的變化約束條件，在matlab中，第n個繞組電流范圍可設為：

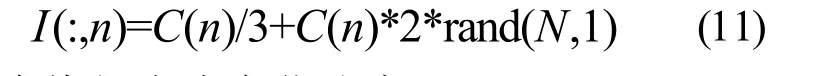
第n個繞組電流變化速度即：

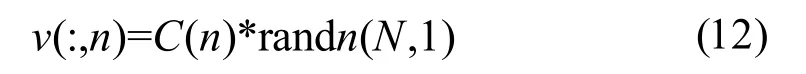
其中N表示粒子數目，C(n)就是IRMS中第n個元素[7]。根據迭代經驗，粒子數取N=400，粒子維數（未知數個數）取D=10，學習因子取c1＝c2＝1.4962，慣性權重w＝0.7298[8]，最大迭代次數取MaxDT＝1 000，目標函數為

可求出繞組電流矩陣:

將補償磁場D2＝A*IPM的曲線與感應磁場B的曲線比較，并作差值求結果磁場E2=D2-B，如圖5。

此時結果磁場最大峰值為0.130單位磁感應強度值，相比最小二乘的最大峰值0.194降低33%，優化效果明顯。此外，由圖6所示的最優解變化圖，可知算法在100步左右迭代就已收斂，運算時間只需12 s左右。

如果不采用最小二乘法進行初步約束，而將粒子位置和速度范圍設定為隨機值，其他條件與上述一致，最優解變化如圖7，可見經過5000步計算，結果仍不收斂，且最優解值較大，為0.345，相比最小二乘法的最大峰值0.194升高78%，且在同一臺電腦上運算需要1分鐘左右。

表1對比了三種求解方法的消磁電流、結果磁場最大峰值、迭代次數和計算時間，說明改進型粒子群法在最優解和收斂速度方面具備綜合優勢。

?

此外，由于基本粒子群算法本身參數的隨機性，連續求解10次，所得最優解每次都不相同，而運用改進型粒子群算法求解，最優解穩定性較高，如表2。

4 總結

本文提出了一種改進型粒子群算法用以調整艦船消磁電流，該算法使用最小二乘法的結果來約束粒子群算法中粒子位置和速度的變化范圍，限定求解空間和粒子速度，可以得到比最小二乘法和基本粒子群法更優的結果磁場，同時該算法直觀易懂、收斂速度快、結果穩定性高，實際算例說明此算法可用于艦船消磁電流的調整優化。

?

[1]張國友.艦船消磁原理及裝置[M].武漢: 海軍工程大學,2009: 68-92.

[2]韋春健,史振宇.德國海軍消磁系統發展現狀及應用[J].船電技術,2013,33(06): 36-38.

[3]唐申生,周耀忠,莊清華.大型艦船分區消磁理論研究[J].海軍工程大學學報,2003,15(1): 80-83.

[4]劉大明.艦船消磁理論與方法[M].北京: 國防工業出版社,2011: 137-138.

[5]J Kennedy,R C Eberhart.Particle swarm optimization.IEEE International Conference on Neural Networks,Perth,Australia,1995.

[6]胡會超.粒子群優化算法研究進展[A].全國冶金自動化信息網2013年會論文集[C],2013: 200-202.

[7]馬莉.MATLAB數學實驗與建模[M].北京:清華大學出版社,2010.

[8]周俊,陳璟華,劉國祥,許偉龍.粒子群優化算法中慣性權重綜述[J].廣東電力,2013,26(7): 6-12.