粗糙集屬性約簡(jiǎn)方法研究

張靜

（江蘇科技大學(xué) 計(jì)算機(jī)科學(xué)與工程學(xué)院，江蘇 鎮(zhèn)江 212003）

粗糙集 （Rough Set）理論由波蘭學(xué)者Z.Pawlak于1982年提出，是一種處理不精確、不相容和不完全數(shù)據(jù)的新的數(shù)學(xué)工具[1]。它已經(jīng)在決策與分析、故障診斷、模式識(shí)別、數(shù)據(jù)挖掘、系統(tǒng)建模、動(dòng)態(tài)目標(biāo)識(shí)別及跟蹤等領(lǐng)域取得了很大的成功[2]。屬性約簡(jiǎn)是粗糙集理論的核心內(nèi)容之一。目前已經(jīng)出現(xiàn)了很多屬性約簡(jiǎn)的方法，例如基于正區(qū)域的屬性約簡(jiǎn)[3]、基于差別矩陣的屬性約簡(jiǎn)[4]、基于信息熵的屬性約簡(jiǎn)[5]、基于分布的屬性約簡(jiǎn)及基于近似的屬性約簡(jiǎn)[6]、基于云模型的約簡(jiǎn)方法[7]、基于相對(duì)粒度的約簡(jiǎn)算法發(fā)[8]等。本文通過(guò)將決策信息系統(tǒng)樹(shù)形化，并定義了在此樹(shù)形結(jié)構(gòu)上的屬性約簡(jiǎn)，發(fā)現(xiàn)屬性可約簡(jiǎn)并不需要再次求得下上近似集，可直接由等價(jià)類所包含的決策屬性來(lái)決定，由此可增加屬性約簡(jiǎn)的效率。進(jìn)而給出了一種基于編碼解空間結(jié)構(gòu)的求粗糙集屬性約簡(jiǎn)最優(yōu)解的算法，并發(fā)現(xiàn)編碼解空間結(jié)構(gòu)對(duì)求取最優(yōu)解及次優(yōu)解均有好處。

1 粗糙集中屬性約簡(jiǎn)滿足的條件

粗糙集的主要研究對(duì)象是決策表，一個(gè)決策表就是一個(gè)決策信息系統(tǒng)。下面是Pawlak關(guān)于決策表以及下上近似集的定義：

定義 1:五元組 S=（U，C，D，V，f）是一個(gè)決策表，其中 U={x1，x2，x3，…，xn}表示研究對(duì)象的非空有限集；D 表示決策屬性C∪D→V是一個(gè)信息函數(shù)，它給U中每一個(gè)對(duì)象的所有屬性賦予信息值，即對(duì)?x∈U，a∈C∪D，有 f（x，a）∈Va；每一個(gè)屬性子集P?（C∪D）決定了一個(gè)二元不可分辨關(guān)系：

IND（P）={（x，y）|（x，y）∈U×U，?a∈P∧f（x，a）=f（y，a）}（1）

關(guān)系 IND（P）構(gòu)成了 U的一個(gè)劃分，用 U/IND（P）表示，簡(jiǎn)記為 U/P，U/P 中的元素[x]p={y|?a∈P，f（x，a）=f（y，a）}稱為 U關(guān)于P的等價(jià)類。

定義 2:在決策表 S=（U，C，D，V，f） 中， 設(shè)?R?C∪D，X?U 記 U/R={R1|R2，…，RL}，則稱 R（X）=U{Ri|Ri∈U/R，Ri?X}為 X 關(guān)于 R 的下近似集，R （X）=∪{Ri|Ri∈U/R，Ri∩X≠φ}為X關(guān)于R的上近似集。

根據(jù)下上近似集的定義可以得出下面兩種基于統(tǒng)計(jì)意義的推理規(guī)則：如果對(duì)象x在R上的值滿足某個(gè)條件，x就屬于X（規(guī)則1）；如果對(duì)象x在R上的值滿足某個(gè)條件，x就不屬于 X（規(guī)則 2）。

考慮到這個(gè)因素，給出了下面兩個(gè)粗糙集屬性約簡(jiǎn)的定義：

定義 3:在決策表中 S=（U，C，D，V，f），若?B?C，并且B（X）=C（X），B（X）=C（X）；?b∈B 均有（B-{b}）（D）≠C（D）或者（B-{b}）（D）≠C（D），則稱 B 是 C 相對(duì)于 D 的強(qiáng)屬性約簡(jiǎn)。 所有C相對(duì)于D的屬性強(qiáng)約簡(jiǎn)的集合記為StrongReduct（C，D）。

定義 4:在決策表中 S=（U，C，D，V，f），若?B?C，并且B（X）=C（X）；?b∈B 均有（B-{b}）（D）≠C（D），則稱 B 是 C 相對(duì)于D的弱屬性約簡(jiǎn)。所有C相對(duì)于D的屬性弱約簡(jiǎn)的集合記為 WeakReduct（C，D）。

強(qiáng)屬性約簡(jiǎn)可以保證約簡(jiǎn)后這兩個(gè)規(guī)則都不變，而弱屬性約簡(jiǎn)只能保證約簡(jiǎn)后規(guī)則1不變。為了得到通過(guò)等價(jià)類判斷屬性是否可被約簡(jiǎn)的規(guī)則，首先給出了決策信息系統(tǒng)的樹(shù)形表示，以及樹(shù)形表示約簡(jiǎn)算法。

2 決策信息系統(tǒng)的樹(shù)形表示以及此樹(shù)形表示約簡(jiǎn)的求解

決策信息系統(tǒng)的樹(shù)形表示：

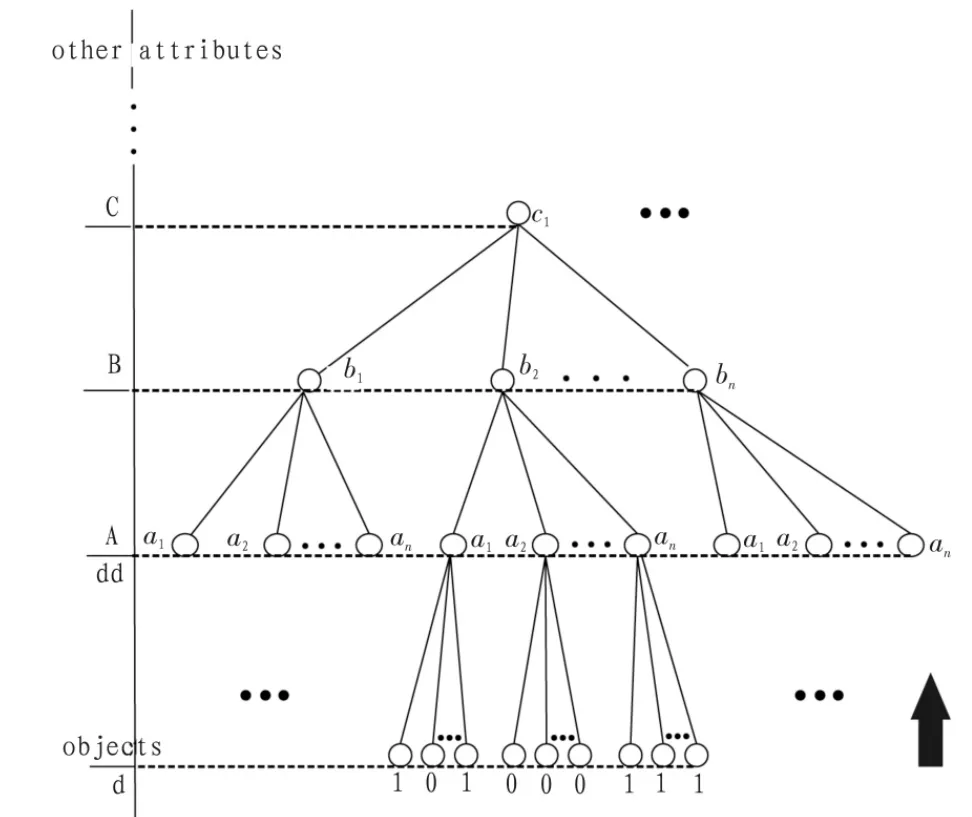
圖1 決策信息系統(tǒng)樹(shù)形表示圖Fig.1 A tree representation of decision information system

此樹(shù)（如圖1所示）是依據(jù)不可分辨關(guān)系建立的。從上往下，除最后一層分別代表屬性層，大寫字母代表屬性（為了以示和屬性集合的區(qū)別用小一號(hào)的大寫字母表示），小寫字母代表屬性的值。最后一層代表對(duì)象層，d代表此對(duì)象的決策屬性值。根據(jù)此表示方法易得，從上至下的每一條路徑pi（如…c1b1a2）代表著一個(gè)等價(jià)類。dd代表等價(jià)類的決策屬性值。?R?C，U/R={R1，R2，…，RL}表示由條件屬性集R對(duì)論域U的劃分，則根據(jù)不可分辨關(guān)系可建立雙射pc:P→U/R，其中P={pi}。 dd（pi）=1 代表著等價(jià)類 pc（pi），pc（pi）?R（X）；dd（pi）=2 代表著等價(jià)類 pc（pi），pc（pi）?R（X）；dd（pi）=0 代表著等價(jià)類 pc（pi），pc（pi）?R（XC）。 若 x 是決策信息系統(tǒng)中的一個(gè)對(duì)象（處于決策信息系統(tǒng)樹(shù)形圖的最底層），則 dd（x）=d（x）。

決策信息系統(tǒng)的樹(shù)形表示約簡(jiǎn)算法：

定義 5:在決策表 S=（U，C，D，V，f）中，A∈C，pi是一條路徑且最后一個(gè)節(jié)點(diǎn)是屬性A中的值如:

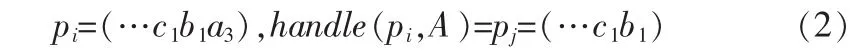
令Path（A）最后一個(gè)節(jié)點(diǎn)是屬性A中的值得路徑的集合，?pi，pj∈Path（A），則 handle（pi，A）=handle（pj，A）。

易證，?pi，pj∈Path（A），pc（pi）?pc（handle（pi，A））并 且pc（pj）?pc（handle（pj，A））。 下面給出由 dd（pi）和 dd（pj）求dd（handle（Path（A）））的算法，如圖 2 所示（易證）：

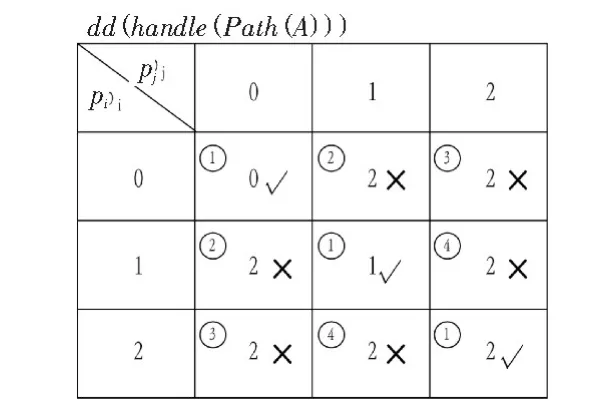
圖 2 dd（handle（path（A）））的取值表Fig.2 Value table of dd（handle（path（A）））

其中 2 的情況會(huì)同時(shí)縮小（C-{A}）（X）和（C-{A}）（XC）（如圖 3 所示）；3 的情況會(huì)縮小 （C-{A}）（XC）；4 的情況會(huì)縮小（C-{A}）（X）；只有 1 的情況是滿足約簡(jiǎn)條件的（如圖 4）。所以當(dāng)滿足2、3、4的時(shí)候?qū)傩圆豢梢员粡?qiáng)約簡(jiǎn)，只有滿足①的情況屬性A才能被強(qiáng)約簡(jiǎn)。這個(gè)結(jié)論也是易證的。有了這個(gè)結(jié)論我們就可以僅僅通過(guò)等價(jià)類和決策屬性就可以判斷在此樹(shù)形表示中是否可被約簡(jiǎn)。

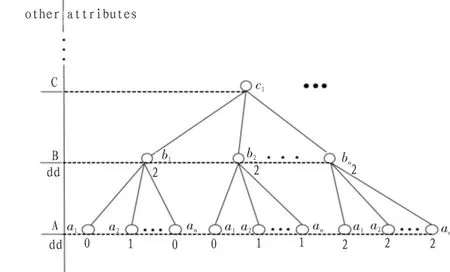
圖3 屬性A不可被強(qiáng)約簡(jiǎn)圖Fig.3 Unable to be strong reduction graph of A

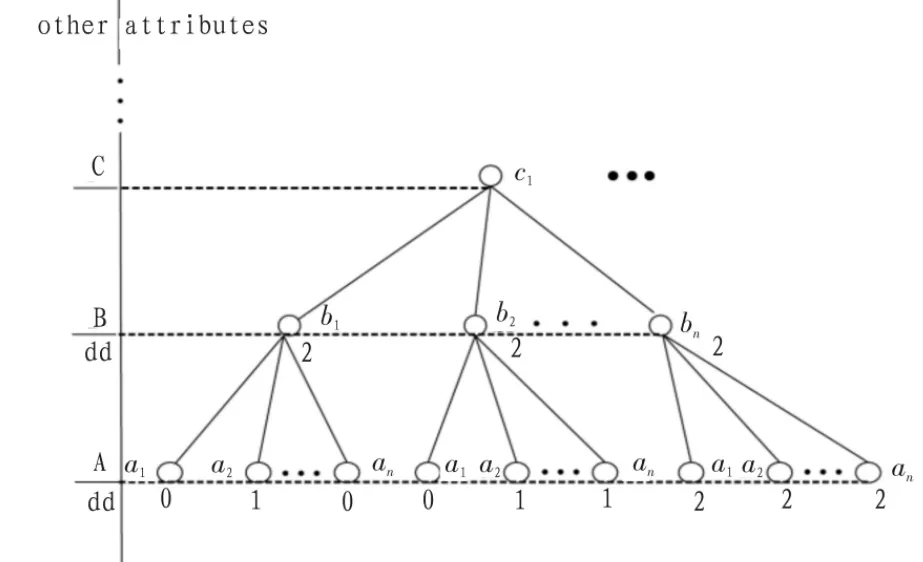
圖4 屬性A可被強(qiáng)約簡(jiǎn)圖Fig.4 Can be strong reduction graph of A

根據(jù)樹(shù)形表示與等價(jià)類之間的關(guān)系可得若某屬性在此表示下可被強(qiáng)約簡(jiǎn)則，它必可在決策信息系統(tǒng)中也可被強(qiáng)約簡(jiǎn)；若某屬性在此表示下不可被強(qiáng)約簡(jiǎn)則，它必可在決策信息系統(tǒng)中也不可被強(qiáng)約簡(jiǎn)。

對(duì)每一個(gè)屬性強(qiáng)約簡(jiǎn)（RE，C-RE），其中C-RE是強(qiáng)約簡(jiǎn)掉的屬性，RE是保留下來(lái)的屬性。Random（RE）是保留下來(lái)的屬性的隨機(jī)排列，Random（C-RE）是強(qiáng)約簡(jiǎn)掉的屬性的隨機(jī)排列（Random（RE），Random（C-RE））。 根據(jù)排列可以畫(huà)出一個(gè)屬性強(qiáng)約簡(jiǎn)的樹(shù)形圖，并根據(jù)此樹(shù)形圖的屬性約簡(jiǎn)又可得到最終的屬性約簡(jiǎn)。（易證）

3 樹(shù)形表示屬性約簡(jiǎn)分析

定義 6:在決策表 S=（U，C，D，V，f） 中，C 相對(duì)于 D 屬性強(qiáng)約簡(jiǎn)的核集定義為

在依據(jù)決策系統(tǒng)樹(shù)形圖的屬性約簡(jiǎn)中，令C相對(duì)于D第一次不可被強(qiáng)約簡(jiǎn)的屬性的集合為NStrongfirst（C，D）。

證明：①?NSfi∈NStrongfirst（C，D）?NSfi∈StrongCore（C，

使用反證法：若?NSfi?∩REj，則?j，NSfi?REj即 NSfi可以被約簡(jiǎn)，由于屬性的約簡(jiǎn)與順序無(wú)關(guān)。所以NSfi可被第一次約簡(jiǎn)。矛盾所以式子成立。

②?SCi∈StrongCore（C，D）?SCi∈NStrongfirst（C，D）

若?SCi∈StrongCore（C，D），SCi不可被任何約簡(jiǎn)，自然不可被第一次約簡(jiǎn)，即SCi∈NStrongfirst（C，D）。 定理證明完畢。

定義 7:在決策表 S1=（U1，C1，D1，V1，f1）中，A1?C1，B1?C1且 A1∪B1=C1，其中 B1={b1，b2，…，bn}。 在決策表 S2=（U2，C2，D2，（V1）bn}，?x∈U2，若 a∈A1∪D1， f2（x，a）=f1（x，a）；若 a=b，f2（x，b）=（ f1（x，b1），f1（x，b2），…，f1（x，bn））。向這樣通過(guò) S1定義 S2的過(guò)程稱為決策表 S1的屬性合并， 記為 S2=AmalAttr（S1，B，b）。其中b是由B合并的屬性。

定理二：有決策表 S1=（U1，C1，D1，V1，f1）、決策表 S2=（U2，C2，D2，V2，f2） 以及屬性集合 A1、B， 其中 A1?C1，B?C1，A1∪B=C1，S2=AmalAttr（S1，B，b），則 C2=A1∪b，IND（S1）=IND（S2）。由決策表的屬性合并的定義以及不可分辨關(guān)系的定義很容易證。

由上面兩條定理可得如下推論：

推論 1：有決策表 S=（U，C，D，V，f），以及屬性集合 A?C和B?C，其中A?B，如果A不可被約簡(jiǎn)，則B也不可被約簡(jiǎn)。

證明：S1=AmalAttr （S，A，a）=（U1，C1，D1，V1，f1）， 其中 C1=（C-A）∪{a}。 由定理二可知 IND（S）=IND（S1）。 根據(jù)上下近似集的定義可知 C（X）=C1（X），C（X）=C1（X）。 由于 C1-{a}=C-A，根據(jù)屬性合并的定義可知 （C1-{a}）（X）=（C-A）（X），（C1-{a}）（X）=（C-A）（X）。由屬性約簡(jiǎn)的定義可知若A在S中不可約，則 a 在 S1中不可約。那么 a∈NStrongfirst（C1，D1）。根據(jù)定理一可知 a∈StrongCore（C1，D1），所以在 S1中任何包含 a 的屬性集都不可約。所以（B-A）∪{a}在S1中不可約。根據(jù)屬性合并的定義可知（C1-（B-A）∪{a}）（X）=（C-B）（X），（C1-（B-A）∪{a}）（X）=（C-B）（X）。 又由于 C（X）=C1（X），C（X）=C1（X），根據(jù)屬性約簡(jiǎn)的定義可知若（B-A）∪{a}在S1中不可約，則B在S中不可約。證畢。

通過(guò)以上的分析可知，某一個(gè)屬性子集是否可被強(qiáng)約簡(jiǎn)可通過(guò)在此信息系統(tǒng)中將此屬性子集合并后得到的信息系統(tǒng)中，由此屬性子集生成的新的屬性在該信息系統(tǒng)樹(shù)形表示中是否可被第一次強(qiáng)約簡(jiǎn)決定。由于在信息系統(tǒng)樹(shù)形表示中屬性的約簡(jiǎn)只由等價(jià)類和決策屬性就可以決定了，所以在信息系統(tǒng)中也可以通過(guò)等價(jià)類以及決策屬性就可以決定了。

若這個(gè)屬性子集不可被強(qiáng)約簡(jiǎn)，則包含它的屬性子集也不可被強(qiáng)約簡(jiǎn)（即可被剪枝，假設(shè)屬性只有ABCD，則屬性子集的剪枝過(guò)程如圖5所示）。若在信息系統(tǒng)樹(shù)形表示中不能被第一次強(qiáng)約簡(jiǎn)，則該屬性屬于信息系統(tǒng)屬性強(qiáng)約簡(jiǎn)的核中。核是不可被約簡(jiǎn)的屬性，除核之外的屬性都是可被約簡(jiǎn)的屬性。

圖5 屬性子集剪枝過(guò)程圖Fig.5 Attribute subset pruning process diagram

4 結(jié) 論

屬性約簡(jiǎn)在粗糙集理論研究中發(fā)揮著巨大的作用。本文從樹(shù)形結(jié)構(gòu)考慮給出了決策信息系統(tǒng)的樹(shù)形表示。基于本文提出的樹(shù)形結(jié)構(gòu)文中進(jìn)一步的得出了一個(gè)判斷屬性是否可被約簡(jiǎn)的好的方法，通過(guò)理論分析，本文提出的屬性約簡(jiǎn)算法可以大大的減少屬性搜索的步驟從而降低屬性約簡(jiǎn)所需要的時(shí)間。

[1]Pawlak Z.Rough Sets-theoretical aspects of reasoning about data[M].Kluwer Acadamic Publisher，1991.

[2]Pawlak Z.A rough set view on Bayes’theorem[J].International Journal of Intelligent Systems，2003，18（5）:487-498.

[3]Pawlak Z.Rough set[J].Communication of the ACM，1995，38（11）:89-95.

[4]Skowron A，Rauszer C.The discernibility matrices and functions in information systems[M].Intelligent Decision Support Handbook of Applications and Advances of the Rough Sets Theory.Kluwer Academic Publishers，1992.

[5]Wang G Y，Yu H，Yang D C.Decision table reduction based on conditional information entropy[J].Chinese Journal of Computer，2002，25（7）:759-766.

[6]Zhang W X，Mi J S，Wu W Z.Knowledge reductions in inconsistent information systems[J].Chinese Journal of Computer，2003，26（1）:12-18.

[7]代勁，何中市.基于云模型的決策表規(guī)則約簡(jiǎn)[J].計(jì)算機(jī)科學(xué)，2010，37（6）:265-267.DAI Jin，HE Zhong-shi.Rules reduction for decision table based on cloud model[J].Computer Science，2010，37（6）:265-267.

[8]徐久成，史進(jìn)玲，孫林.一種基于相對(duì)粒度的決策表約簡(jiǎn)算法[J].計(jì)算機(jī)科學(xué)，2009，36（3）:205-207.XU Jiu-cheng，SHI Jin-ling，SUN Lin.Attribute reduction algorithm based on relative granularity in decision tables[J].Computer Science，2009，36（3）:205-207.