基于SCM模型的信道預測方法

張忠培，董琪玲

(電子科技大學通信抗干擾技術國家級重點實驗室，四川成都611731)

0 引言

在移動通信中，反射、繞射和散射普遍存在于各種環境，不可避免存在多徑傳播;發射端與接收端的相對移動，又不可避免的產生多普勒擴展。由于寬帶無線信道中的多徑擴展和多普勒擴展，使寬帶無線信道呈現出頻率選擇性和時變特性，從而使無線傳播環境變得復雜。惡劣的無線傳播環境會導致傳輸信號失真。為了降低系統存在的符號間干擾和誤碼率，通常利用信道估計得到的信道信息進行預編碼或接收信號均衡。但是對于快速時變信道，利用傳統的基于判決反饋的信道估計方法得到的信道信息是過時的，不足夠反映當前的信道狀況。因而，為了提升體統性能，利用信道預測較準確地得到信道的變化趨勢，從而獲得未來信道較為準確的狀態信息很有必要。

信道預測是指根據信道當前和過去的信道信息對未來的信道信息進行預測。信道預測分長期預測和短期預測兩種。短期預測利用當前和先前相鄰幾幀的信道信息準確預測下一幀的信道信息，預測效果較好。長期預測是預測信道間隔較長一段時間后的信道信息的變化情況，通過長期預測可以明確信道是在變好還是變壞，這種變化信息可為多種自適應算法提供參考。信道長期預測的意義即在于:無論信道變化快還是慢，信道長期預測可以根據先前間隔相同幀數的信道增益預測出將來間隔同樣幀數的信道增益，進行自適應處理，而利用信道估計方法卻無法得到未來的信道信息。文中的預測方法為短期預測方法。

現存的諸多信道預測方法，雖然能夠較為準確地預測信道的變化趨勢，卻并不關注信道預測技術在現實場景中的實用性問題。信道預測技術的現實工程意義在于:減小系統資源開銷，使信號發送端獲取更為準確的信道信息。在信道時變性較大時，系統為了保證所獲取的信道信息準確性，需要增加信道估計的頻率，這就需要系統在單位時間內使用更多的導頻來進行有效的信道估計。這會增加系統資源開銷，降低系統傳輸速率。如果能夠融合有效的信道預測算法，就可以通過使用信道預測，在盡量不損失所獲信道信息精確度的前提下減少信道估計頻率，從而實現單位帶寬內更多信息的傳輸，減小系統資源開銷。

大量文獻表明，無線信道具有時域相關性。考慮到信道的時域相關性，基于信道的時域相關性提出兩種信道預測方法，給出信道預測的最佳表達式。此外，由于目前SCM(Spatial Channel Model)信道模型是最接近真實信道的信道模型，文中所展現的信道時域相關性都是基于SCM信道模型的仿真得到。采用這種模型進行分析也使得所提出的算法更具有實用性。還使用MATLAB仿真了根據提的兩種信道預測算法預測所得信道信息與實際信道信息的MSE值，并與現有協議下系統所持信道信息與實際信道信息的MSE值進行對比分析。

后續內容組織如下:第一節闡述信道的時變性對系統的影響;第二節通過數值仿真分析SCM信道的時域相關幅度特性與相位特性，此類特性能夠很大程度上決定信道預測方法的設計;第三節基于第二節中信道的時域相關特性，提出兩種信道預測算法;第四節對兩種信道預測算法的性能進行仿真和分析。

1 信道的時變性對系統性能的影響

為了闡述信道預測的重要性，先分析信道時變對通信系統性能的影響。圖1為SISO-OFDM下行系統鏈路。在此系統中，用戶以一定的速度移動，不同的移動速度將導致信道不同程度的時變。

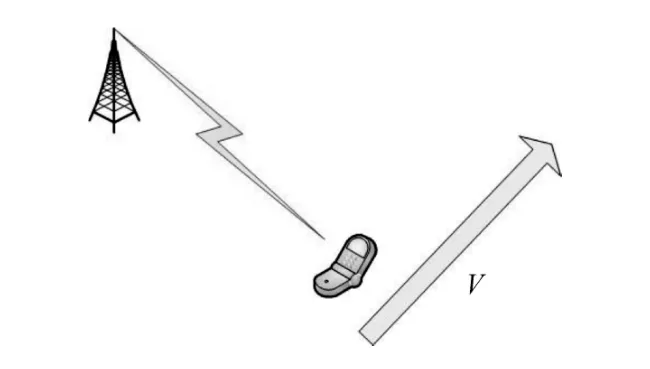
圖1 SISO時變系統傳輸圖

在OFDM系統中，傳輸時域信號x( tn)可以由發送數據d(fp)做N位IFFT得到

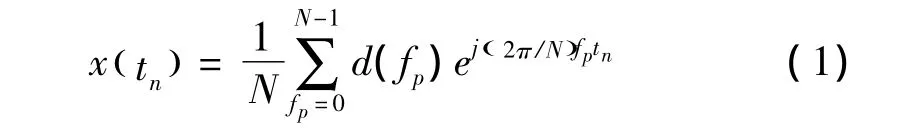
其中d(fp)代表子載波fp上的傳輸數據，tn是對應的時間參數。

接收端得到的時域信號y(tn)由時域信號經歷M條徑傳輸，在接收端疊加上白噪聲后得到

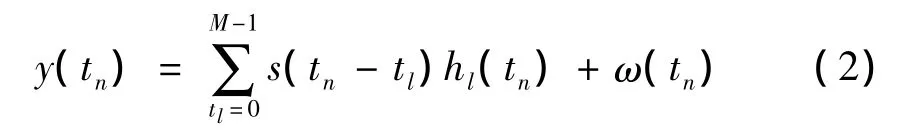
其中hl(tn)代表信道對應tn時刻路徑l的沖擊響應。對y(tn)做FFT，得到接收端對應子載波fk的頻域信號

一般認為多徑數目遠遠小于FFT數目，即M?N，因此對應時刻tn和載波fp的信道響應表達式為

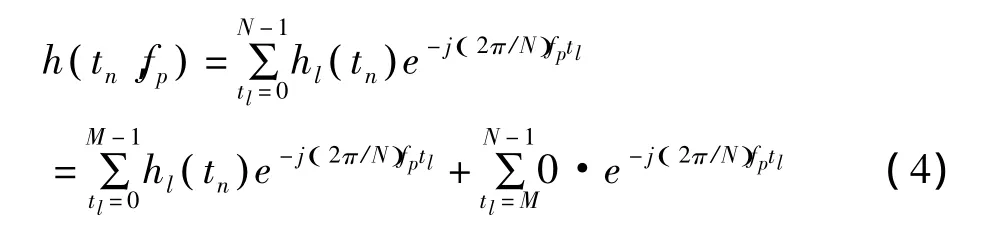
進一步可以得到s( fk)關于 h ( tn，fp)的表達式

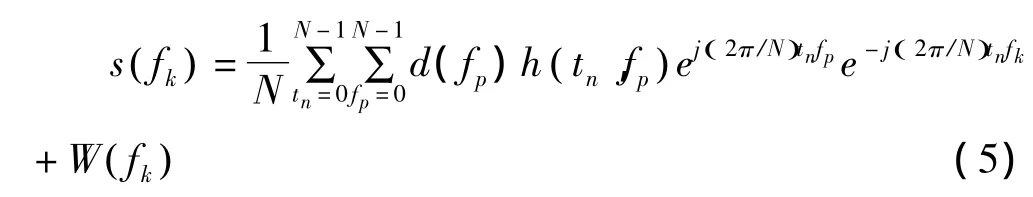
在時域慢衰落信道條件下，往往認為兩次信道估計之間，無線信道保持不變。系統會使用同一h(tn，fp)進行傳輸調制與解調。

因此，在時域慢衰落信道條件下，接收信號的頻域表達式為

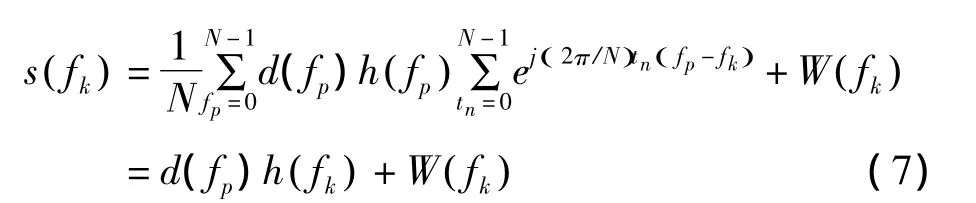
系統只要通過信道估計，在OFDM符號時隙初期獲得信道參數h( fk)，即可恢復發送數據d(fp)。

而現實系統中，不可忽略的是系統中發送/接收端或者反射體間存在相互移動，這就會導致信道的時變性較大。一旦無線信道的時變較為劇烈，信道不再保持不變。

在信道時變性不可忽略的情況下，s( fk)的表達式如下

大量文獻研究表明，可以將信道短時間內的變化視為線性過程，即只要滿足fdTOFDM＜0.1，(htn，fp)可以被近似線性描述

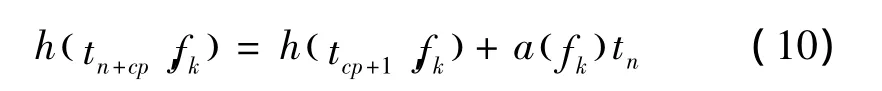
此外，假定系統能夠通過信道估計獲取第一個OFDM數據起始處的準確信道信息h( tcp+1，fk)。

根據式(10)可得到s( fk)表達式為

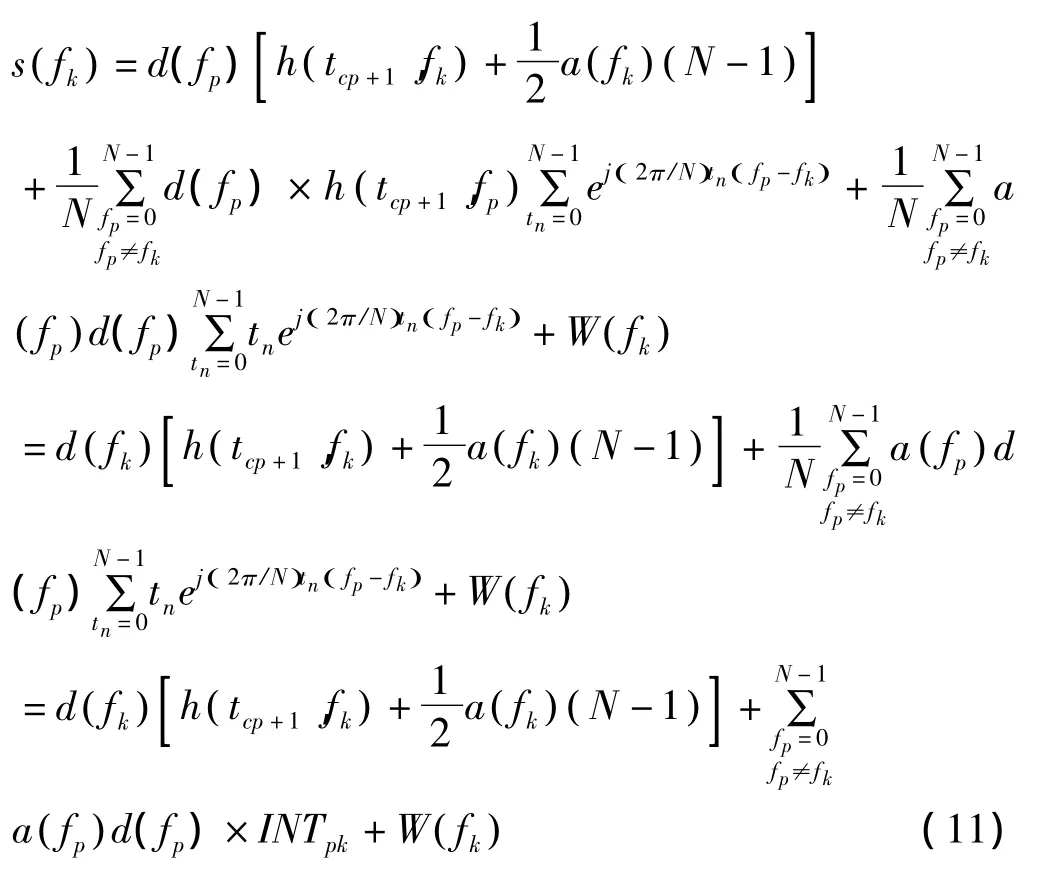
2 信道的時間相關性的幅度特性與相位特性

圖2為信道的時間相關性的幅度特性圖。圖中實線為采用SCM模型生成的信道值的相關性的幅度和歸一化傳播距離的關系圖，虛線表示相關性幅度值的理論值的曲線圖，此理論值為零階貝瑟爾函數，此函數在圖中的第一段可以用二次函數來近似。

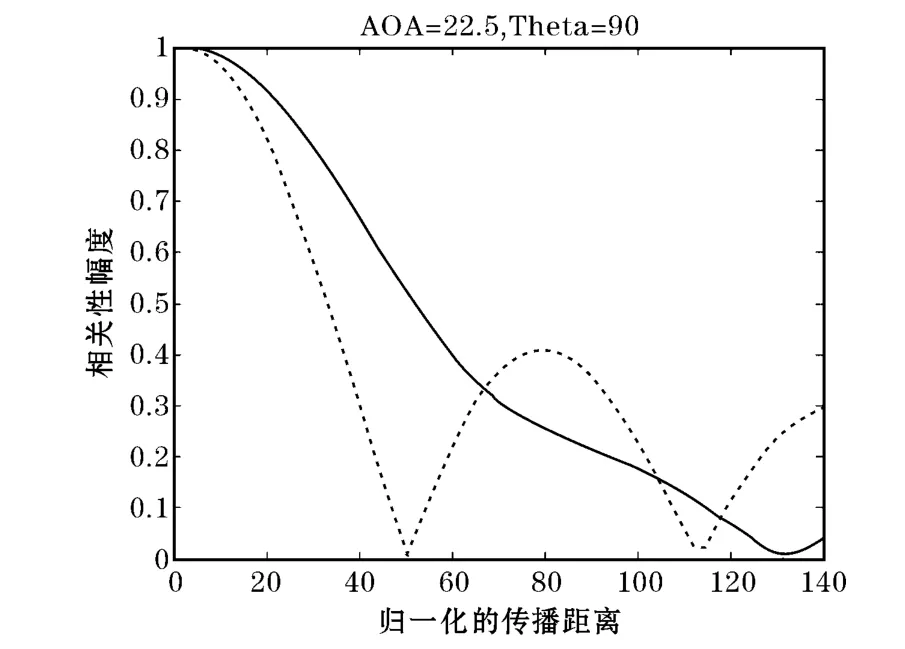
圖2 信道的時間相關性的幅度特性圖

假設第一次信道估計值為h( T－2，fk)，按照現有協議規定，每兩個OFDM時隙做一次信道估計，則當前時刻的信道值h( T ，fk)為第二次信道估計的信道值，而 h( T +1，fk)為下一時刻的信道值。假設信道相位線性變化，圖3為h( T +1，fk)和 h( T ，fk)分別針對 h( T－2，fk)的相位差的概率分布圖，從圖中可見，相位差集中在0附近。這為進行信道預測時將相移假定為線性提供一定依據。

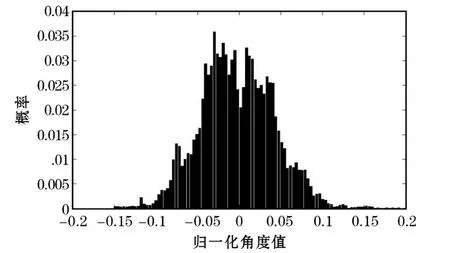
圖3 信道相對相位差的概率分布圖

3 預測方法解析

由于信道時變性對OFDM系統會產生較大的影響，提出兩種基于信道時間相關性的信道預測算法對信道進行預測。

這兩種信道預測算法都是根據系統已經獲知的當前時刻信道信息h( T ，fk)推導對應下一OFDM時隙的對應時刻信道預測值( T +1，fk)，并假設引起的信道預測誤差為 ε( T +1，fk)，不妨假設(T+1，fk)滿足

其中 γ1為預測更新因子，Δh( T ，fk)=h( T ，fk)－h( T－2，fk)，h( T－2，fk)表示對應當前時刻的上一次信道估計所獲得的信道參數值，h( T ，fk)表示當前時刻信道估計獲得的信道參數值。

則 ε ( T +1，fk)滿足

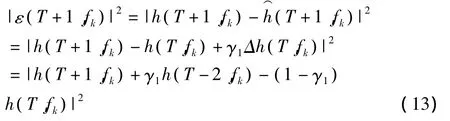
對于信道相關性變化趨勢的分析，采用線性外推法和二次外推法兩種方法進行推導，線性外推法即將信道相關性的變化趨勢視為線性過程進行分析，而二次外推法將變化趨勢擬合為某未知二次函數進行分析。

當前時刻與下一OFDM符號間的信道時域相關性表達式可以表示為

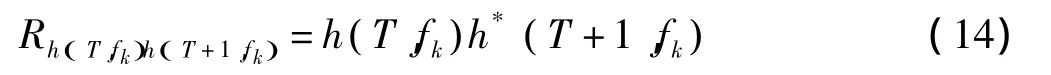
3.1 線性外推法

使用線性外推法，視信道時間相關性的變化為線性變化，可以根據前兩次信道估計所得的信道值推導出的值。

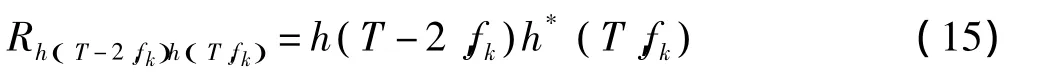
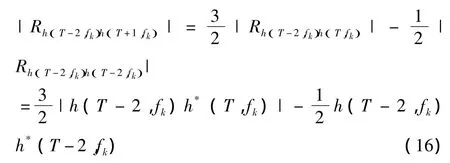
再次利用信道時域相關的幅度特性的線性性質，可以得到

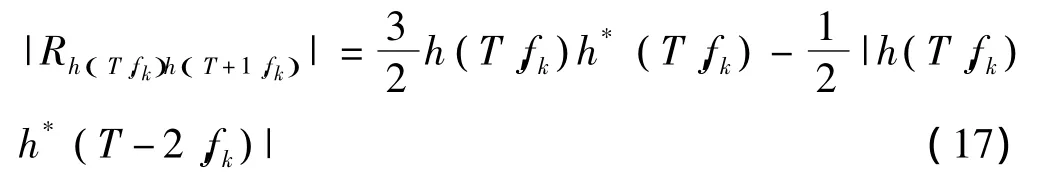
此外，|Rh(T+1，fk)h(T+1，fk)|可以通過|Rh(T，fk)h(T+1，fk)|與|Rh(T，fk)h(T，fk)|得到

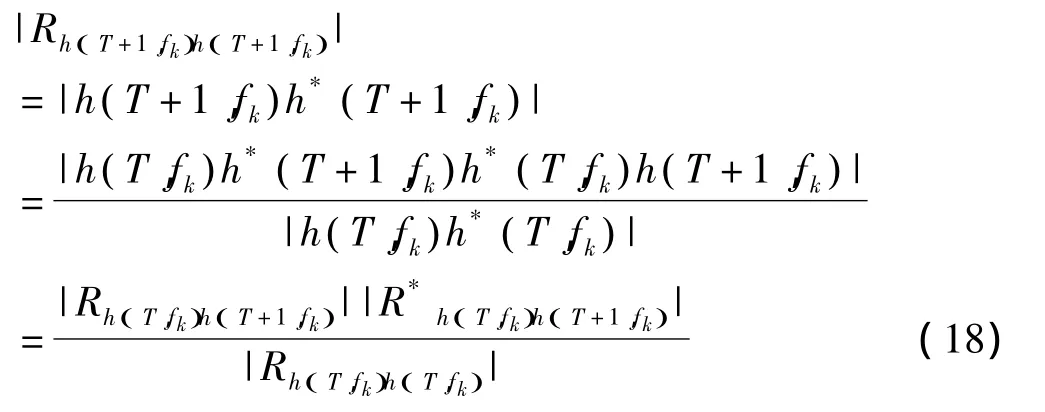
結合式(17)、(18)可以得到

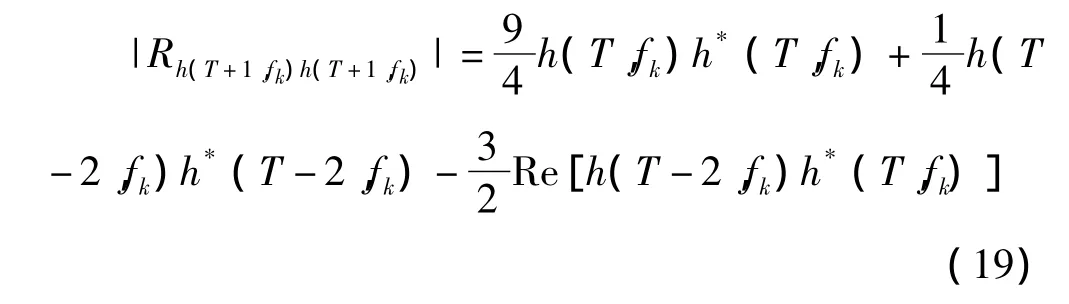
此外，根據圖3的結果，可見將相對相位假設成線性是合理的，于是有

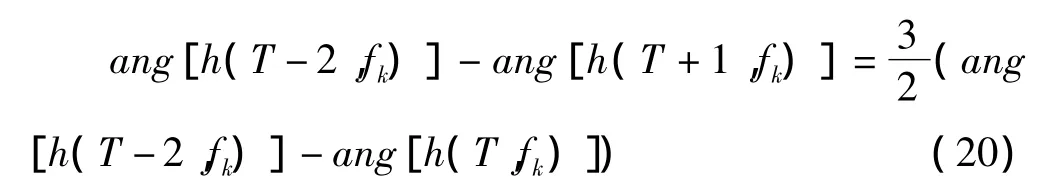
將式(16)、(17)、(19)、(20)代入式(13)，并對|ε ( T +1，fk)|2求導、令導數值為零得到線性外推法下預測更新因子的最優值為

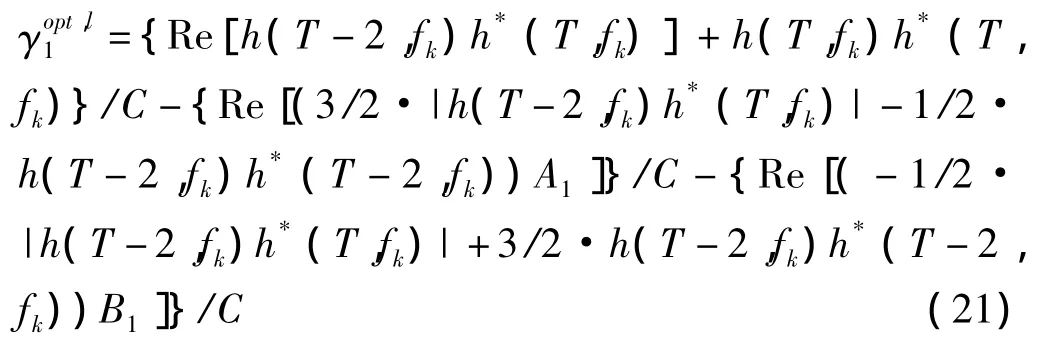
其中，

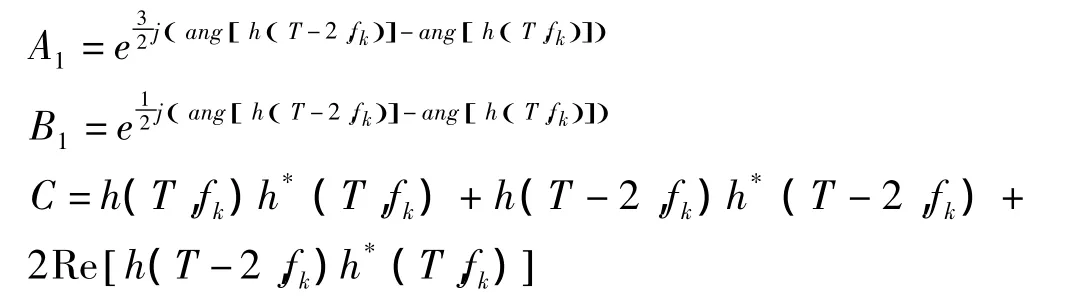
3.2 二次外推法

使用二次外推法，視信道時間相關性的變化為二次變化，在假設信道相關性的幅度為二次關系的前提下，與對應時間呈二次函數關系，根據圖2中仿真得到的信道相關性的幅度特性圖，于是有

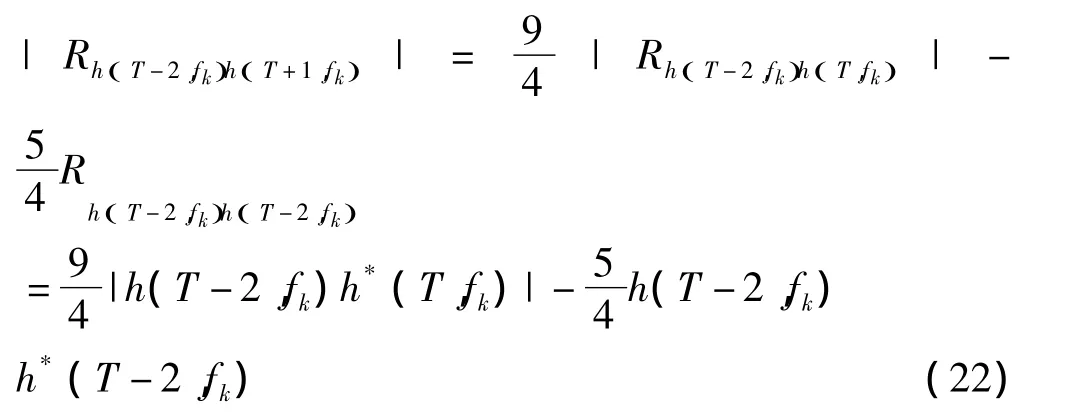
進一步可以得到

將式(22)、(23)、(24)、(20)代入式(13)，并對求導、令導數值為零得到二次外推法下預測更新因子的最優值為

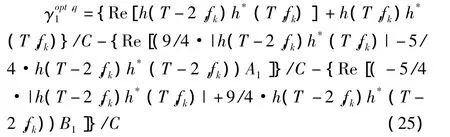
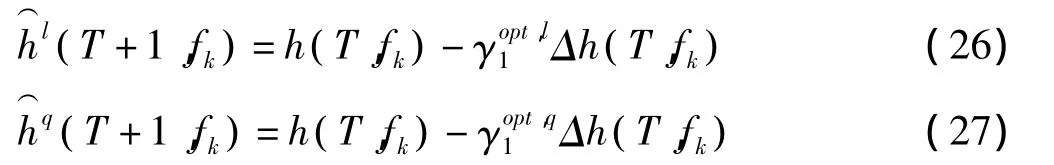
其中:Δh( T ，fk)=h( T ，fk)－h( T－2，fk)

依照式(26)、(27)，系統就可以利用當前信道估計值和上一次信道估計值根據線性外推和二次外推對未來信道信息進行預測，而不是簡單的將未來時刻的信道信息視為保持h( T ，fk)不變。這樣就實現了對信道信息的校正，使得系統用于預編碼等操作的信道信息更接近真實值。

4 仿真結果及分析

按照現有LTE標準，每兩個OFDM時隙做一次信道估計，將兩次信道估計之間的信道視為保持不變，然而，由前面的分析可知，當用戶存在一定的移動速度時，信道的時變性會較明顯，此時將兩個OFDM時隙間的信道視為時不變、采用同一個估計的信道值進行預編碼等操作，會對系統性能造成不利影響。而通過本文的信道預測算法，可以預測各個OFDM符號處的信道信息，而不是簡單的將信道視為同一個估計值。本部分將通過MATLAB仿真來驗證算法的性能。本次仿真基于SCM信道模型，仿真比較了用戶在不同移動速度下，系統采用二次外推法和線性外推法進行信道預測所得的信道估計值與實際信道的MSE值。此外，還與不采用信道預測算法、只是簡單地認為兩個OFDM時隙間信道時不變情況下的信道值與實際信道的MSE值。仿真參數如表1所示，仿真結果如圖4所示。

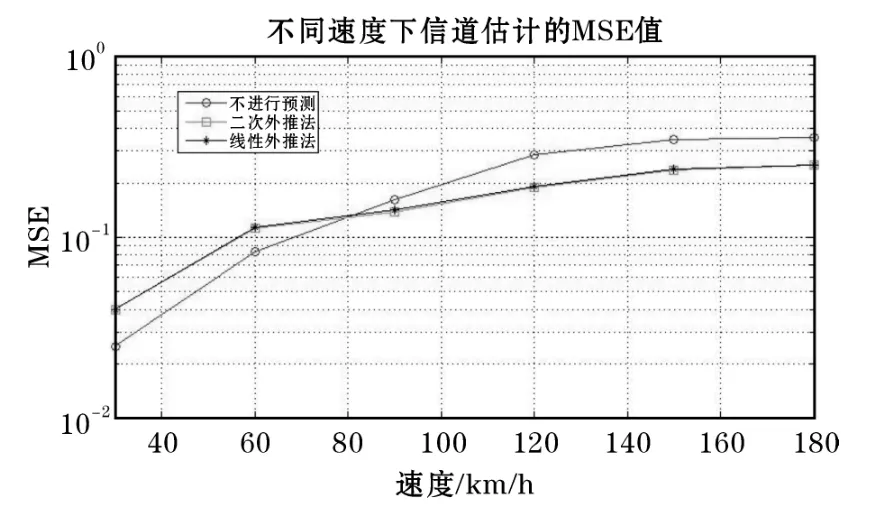
圖4 不同算法下信道估計的MSE值

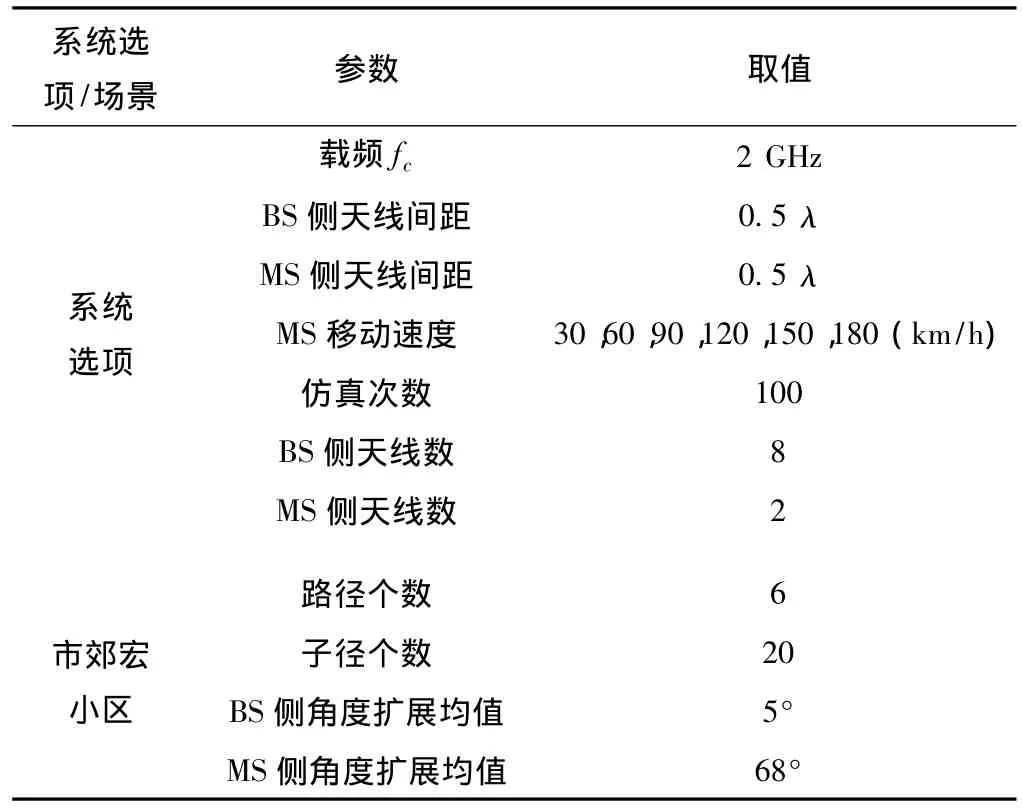
表1 仿真參數

由圖4可見，在用戶速度較高時，采用所提的兩種信道預測算法能使信道估計的MSE值減小，并且線性外推法和二次外推法的性能基本一致。還可以看到，在用戶移動速度較小時，采用信道預測算法并不能降低信道估計的MSE值，這是由于，在用戶移動速度較小時，信道的時變性主要由隨機性因素造成，多普勒頻移造成的影響還比較小，而所提出的兩種算法都是針對多普勒頻移對信道的時變性造成的影響而設計的，因而在用戶移動速度較大時，多普勒頻移對信道時變性的影響占主導因素，因而提出的兩種預測算法能降低信道估計的MSE值。

[1] Wong I C，Evans B L.Sinusoidal Modeling and A-daptive Channel Prediction inMobile OFDM Systems[J].Signal Processing，2008，56(4):1601－1615.

[2] Tan S，HiroseA. Low-calculation-costfading channel prediction using chirp Z-transform[J].E-lectronics Letters，2009，45(8):418－420.

[3] Heidari A，Khandani A K，McAvoy D.Adaptive Modeling and Long-Range Prediction of Mobile Fading Channels[J].IET Communications，2010，4(1):39－50.

[4] Falahati S，Svensson A，Ekman T.Adaptive modulation systems for predicted wireless channels[J].Communications，IEEE Transactions，2004，52(2):307－316.

[5] Shengli Zhou，Giannakis G B.How accurate channel prediction needs to be for adaptive modulation inRayleigh MIMO channels[J].Acoustics，Speech，and Signal Processing，2003.Proceedings.(ICASSP＇03).2003，4:4－81.

[6] Schafhuber，Dieter，Matz G.MMSE and adaptive prediction of time-varying channels for OFDM systems[J].Wireless Communications，2005，4(2):593－602.

[7] Khrwat A S，Sharif B S，Tsimenidis C C.Channel prediction for precoded spatial multiplexing multiple-input multiple-output systems in time-varying fading channels[J].Signal Processing，2009，3(6):459－466.

[8] Viet-Ha Pham，Xianbin Wang，Nadeau J.Long Term Cluster-Based Channel Envelope and Phase Prediction for Dynamic Link Adaptation[J].Communications Letters，2011，15(7):713－715.

[9] Oien G E，Holm H，Hole K J.Impact of channel prediction on adaptive coded modulation performance in Rayleigh fading[J].Vehicular Technology，2004，53(3):758－769.

[10] W Weichselberger，M Herdin，H O¨zcelik，et

al.A stochastic MIMO channel model with joint correlation of both link ends[J].IEEE Transactions on Wireless Communications，2006，5(1):90－99.

[11] Cheng Xiang Wang.Spatial-Temporal Correlation Properties of the 3GPP Spatial Channel Model and the Kronecker MIMO Channel Model[Z].EURASIP Journal on Wireless Communications and Networking，Volume2007，Article ID 39871，9 pages.National Institute of Standards and Technology，Valiated FIPS 140-1 and FIPS 140-2 Cryptographic Modules，2011.