一維大地電磁Occam反演拉格朗日乘子的搜索

張君濤，周 軍，王緒本，夏時斌，鐘紅梅

（1.成都理工大學地球探測與信息技術教育部重點實驗室，成都 610059；2.四川省核工業地質調查院，成都 610061）

一維大地電磁Occam反演拉格朗日乘子的搜索

張君濤1，周 軍1，王緒本1，夏時斌1，鐘紅梅2

（1.成都理工大學地球探測與信息技術教育部重點實驗室，成都 610059；2.四川省核工業地質調查院，成都 610061）

在大地電磁反演中，Occam法因其在反演穩定性和模型分辨率等方面的優勢，得到廣泛應用。但由于其每次迭代都需要不斷地搜索拉格朗日乘子，因而拉格朗日乘子的搜索效率對Occam法反演的運算速度起著至關重要的作用。為提高拉格朗日乘子的搜索效率，這里提出將拉格朗日乘子的搜索從自然數域中轉到以10為底的對數域中進行，同時在區間最小值的搜索中采用二次函數極小值搜索法。通過大量一維大地電磁反演驗證，該方法將拉格朗日乘子的搜索效率提高了20%～50%，大大提高了Occam反演的運算速度，方便了其在高維反演中的應用。

大地電磁；Occam反演；拉格朗日乘子；對數；二次函數搜索

0 引言

在大地電磁反演中，利用目標函數梯度信息的最優化方法占據著主要的地位［1－3，9］，包含Occam法［4－5］、非線性共軛梯度法（NLCG）［7］、擬牛頓法等反演方法。其中Occam法因其在反演穩定性和模型分辨率等方面的優勢，在現今的大地電磁反演中得到了廣泛地應用，但由于該方法在每次反演迭代中，都要搜索一個滿足數據誤差最小或者模型粗糙度最大的拉格朗日乘子，因而需要進行多次正演，增加了反演的計算量，限制了其在高維反演的應用。

很多學者在優化Occam反演的計算量上做了大量的研究，Siripunvaraporn［6－7］等研究了數據空間Occam反演，并且成功的應用到了MT二維、三維反演，極大的加強了Occam法在二維、三維反演中的應用；吳小平［11］等在討論了Occam反演中數據擬合差隨拉格朗日乘子變化的基礎上，采用拉格朗日乘子在一定步長下逐次遞減的求取方法，每次迭代只需一次正演，極大地提高了計算速度，但初始拉格朗日乘子及減小比例的設定對反演穩定性及結果影響較大。在對拉格朗日乘子搜索方式的改進上，也有很多人提出了改進方式［12－13］，但依然有很多地方值得探討。

基于上述考慮，作者對Occam法反演中提高拉格朗日乘子的搜索效率上做了進一步研究，結合拉格朗日乘子在Occam方法反演迭代中的變化特性，提出了對該參數應當采用對數變換，并結合二次搜索方法來開展搜索計算。將上述方法應用到了一維Occam反演的拉格朗日乘子搜索中，試圖提高拉格朗日乘子搜索的計算速度。這里首先介紹了Occam法反演的原理，然后詳細介紹了對數二次法搜索原理，并進行一維模型算例分析，說明了其快速搜索的優勢。

1 Occam反演基本原理

一維Occam反演的目標函數包含數據目標函數和模型粗糙度函數：

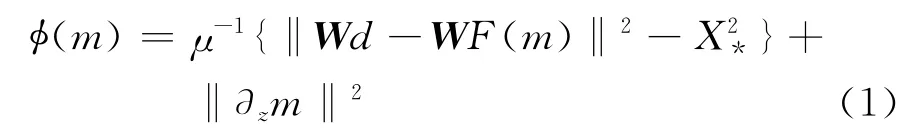
其中：μ為拉格朗日乘子；大括號內的為數據目標函數：d為實測數據；F為正演算子；W為數據誤差加權矩陣；X＊為擬合差期望值；‖?zm‖2為模型粗糙度函數。

反演的過程就是尋找使目標函數得到最小值的模型。為此Occam法將正演算子F線性化，在初始模型m0處按一階泰勒級數展開：

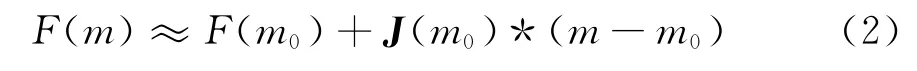
其中：J（m0）為正演算子F對模型參數m0的導數，稱為雅可比矩陣。將式（2）帶入式（1）中，由此得到的目標函數已經簡化為一個關于模型參數m的二次函數：

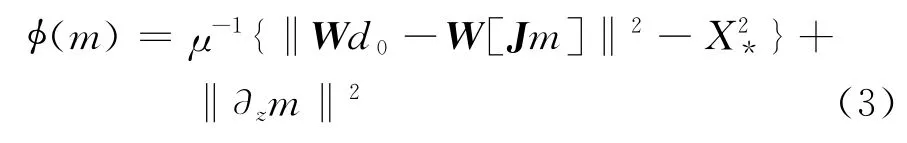
其中：d0＝d－F（m0）＋Jm0，J＝J（m0），再求式（3）關于m的一階導數，得到梯度函數g（m）：

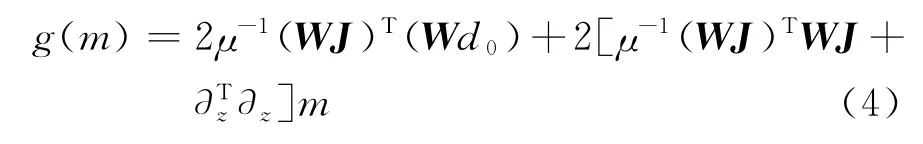
此時的梯度函數是一個關于模型參數的一次函數，令梯度g（m）＝0，求得的模型參數即為目標函數取得極小值的模型：

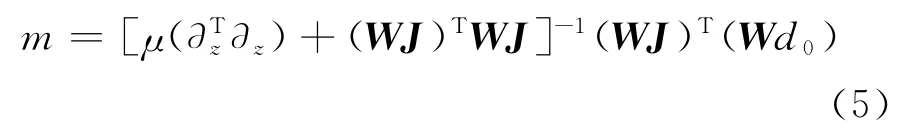
由于正演算子是非線性的，目標函數也不是二次函數，故反演過程中需要不斷迭代，反復修正初始模型m0，重復式（5）過程，最終求得目標函數的最小值。

在每次迭代中，對于不同的拉格朗日乘子u，利用式（5）可得到不同的模型參數及其相應的絕對擬合誤差。相比其他反演方法直接輸入一個經驗的拉格朗日乘子，Occam法反演提出在每次迭代中都要通過搜索，得到一個滿足數據擬合誤差最小的μ值（如果數據擬合誤差低于目標擬合誤差，則搜索滿足目標數據擬合差的最小模型粗糙度的μ值）。用此μ值求得模型參數m再作為下一次迭代的初始模型，進行第二次迭代。這樣反復迭代，最后找到一個滿足目標擬合差且粗糙度最小的模型，或者是達到最大迭代次數后得到的擬合差最小的模型。正是由于Occam法反演對拉格朗日乘子的搜索，使其具有很高的反演穩定性和模型分辨率，但同時也增加了反演的運算量。

2 拉格朗日乘子的搜索方法

考慮到拉格朗日乘子的搜索效率對Occam法反演運算時間的巨大影響，作者對拉格朗日乘子的搜索方式進行改進。

所有患者采用隨機數字表法分為舌下含服組和口服組,每組各40例。口服組患者口服酒石酸美托洛爾片(阿斯利康制藥有限公司,產品批號1407184)25 mg(1片);舌下含服組患者舌下含服酒石酸美托洛爾片25 mg(1片)。

對于μ值的搜索，一般采用先搜索到一個谷值區間，然后在此區間上搜索數據擬合差的最小值，搜索到最小值后進行下一次迭代；而在搜索過程中，一旦有數據擬合誤差小于目標擬合誤差就直接進入滿足擬合差的最小模型粗糙度的μ值搜索。這里也采用以上搜索策略，但做了兩點改進。

2.1 拉格朗日乘子對數化搜索

理論上μ值可以為大于“0”的任意數，但如果直接對μ進行搜索，在區間搜索過程中，μ值的修正步長是隨著μ值的變化而變化的，且初始μ值如果給的不合適，區間搜索的次數會相對較大。考慮到將原目標函數中的拉格朗日乘子μ變為10λ后，并不會改變其原有目標函數的極值特性，只要滿足μ＝10λ其對應的模型參數及其對應的目標函數與數據擬合差都是一致的，因而作者大膽設想將μ值做對數變化，從而將目標函數中對μ值的搜索轉為對10λ中的λ做搜索。將μ＝10λ代入到目標函數式（1）中得式（6）。

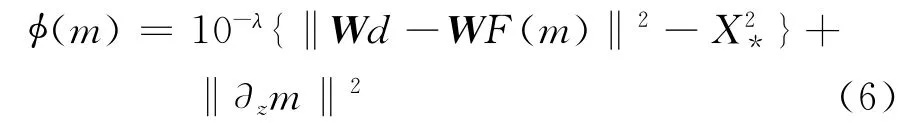
式（6）經過式（3）、式（4）、式（5）運算過程可得每次迭代中模型參數的求取公式：

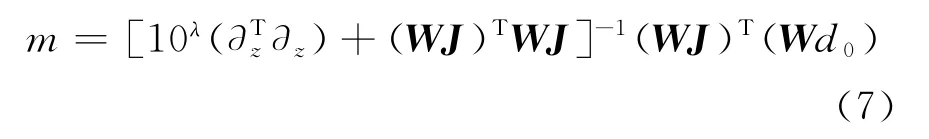
可以看出式（7）只是將式（5）中的μ變為10λ，從而將對μ的搜索轉為對λ的搜索，這將更加快速地搜索到谷值區間，并減小初始λ值對搜索效率的影響。

從圖1可以看出，圖1（a）絕對擬合誤差曲線整體上變化平緩，更近似一個二次曲線；如果我們將區間搜索步長在以10為底的對數上設為“1”，一般在左右幾個步長之內就能搜索到谷值區間，從而擺脫了初始值的設定對搜索次數的影響。圖1（b）絕對擬合誤差曲線在最小值左右變化相當劇烈，而在μ值較大時變化相當平緩。這給區間搜索步長的確定帶來很大的不便，且初始μ值對區間搜索的次數有很大的影響。正是基于上述因素，這里更加明確將拉格朗日乘子的搜索從自然數域中轉到了以10為底的對數域進行，將拉格朗日乘子變化為μ＝10λ，從而將對μ值的搜索改為對λ的搜索，其實質就是在以10為底的對數上進行μ值搜索。為便于進行谷值區間最小值搜索，將搜索到的谷值區間三點按λ值從大到小保存為（λ0，rms0）、（λ1，rms1）、（λ2，rms2）。

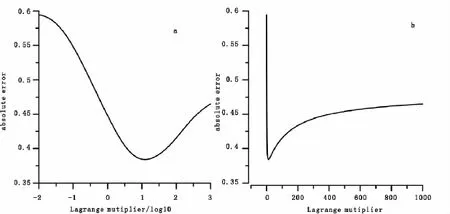
圖1 模型一首次迭代絕對擬合誤差曲線Fig.1 The absolute error curve of the first iteration of the model 1 （a）拉格朗日乘子以10為底；（b）拉格朗日乘子用自然數

2.2 二次函數搜索區間極小λ值

做了上述變化后能快速地搜索到一個谷值區間，但此區間的范圍相對自然數搜索的區間較大，如果區間最小值搜索繼續使用二分法進行，則搜索次數相對自然數搜索的谷值區間二分法，增加了很多次。同樣以圖2（a）為例，首次迭代對數搜索區間次數為4次，但用二分法進行區間最小值搜索則用了8次，共計12次；自然數區間搜索用了9次，但最小值搜索只用了5次，共14次；二者相比，對數搜索基本沒有優勢。因此，提出利用二次函數極小值來搜索區間最小值。

構建二次函數：

本文對于退出搜索需要滿足以下要求：

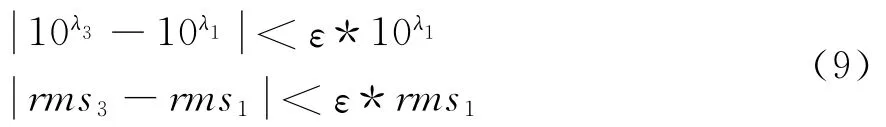
其中ε≤1。當滿足式（9）要求后，則取擬合差小的λ值及其相對應的模型進入下一次迭代。

3 算例分析

為了驗證本方法的搜索效率，建立了四種地電模型（圖2）。特別說明模型一為陳小斌［10］在自適應正則化反演中的八層驗證模型，這里利用此模型將本方法與傳統拉格朗日乘子二分法的搜索過程進行了詳細地比較。四個模型的反演目標擬合差均為0.001。為便于敘述，將作者所描述的搜索方法稱為“對數二次法搜索”，將傳統拉格朗日乘子二分法的搜索稱為“自然二分法搜索”。

表1為八層模型在首次迭代中的μ值變化過程，對數二分法只經過4次區間搜索加3次最小值搜索就完成了迭代，而自然二分法經歷了9次區間搜索加5次最小值搜索才完成迭代。而從搜索的結果來看，兩種方法搜索到的μ值基本上沒有差異，甚至本例中對數二次法搜索得到的絕對擬合誤差還更小一點。可見對數二分法在搜索上的優勢，這種優勢在首次迭代中體現得最為明顯。

圖2 地電模型及Occam反演結果Fig.2 The geoelectric model and Occam inversion results （a）模型1；（b）模型2；（c）模型3；（d）模型4

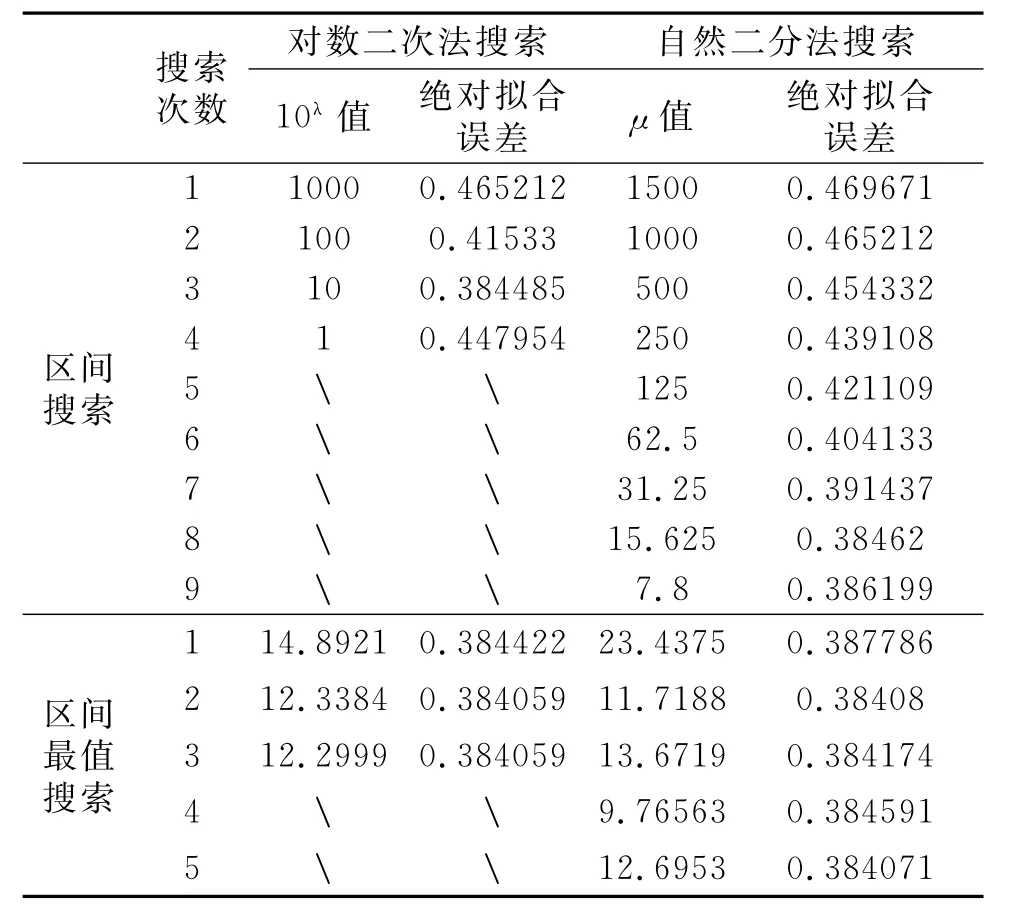
表1 模型1首次迭代μ值搜索過程Tab.1 The searching process of Lagrange multiplierin first iteration of model 1

表2、表3分別為模型一Occam反演用對數二次法搜索與自然二分法搜索的詳細迭代過程。結果可以看出，對數二次法區間搜索往往只需要3次～4次，而3次搜索已經是區間搜索的極限；二次最小值搜索基本上也只需要1次～3次。整體對比，每次迭代對數二次法搜索的次數都明顯少于自然二分法搜索。

表4為四種模型分別用兩方搜索法進行Occam反演的μ值變化次數對比。無一例外，對數二次法搜索次數均少于自然二分法搜索，減小比例在20% ～50%之間。

從圖2反演結果上看，本方法在提高μ值搜索效率的同時，對Occam反演的結果沒有任何影響。

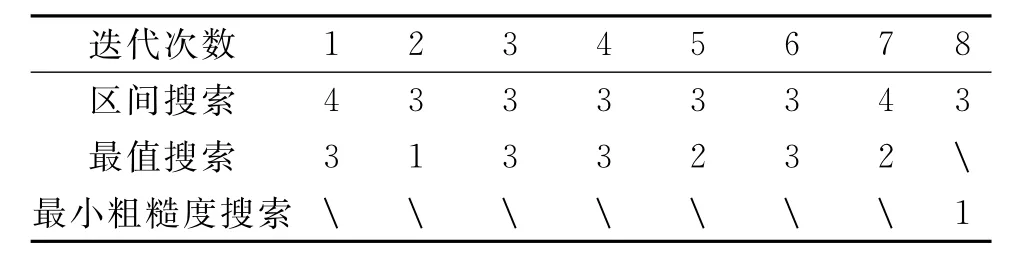
表2 模型1每次迭代對數二次法搜索次數Tab.2 The search process of each iteration of model 1by logarithmic quadratic method

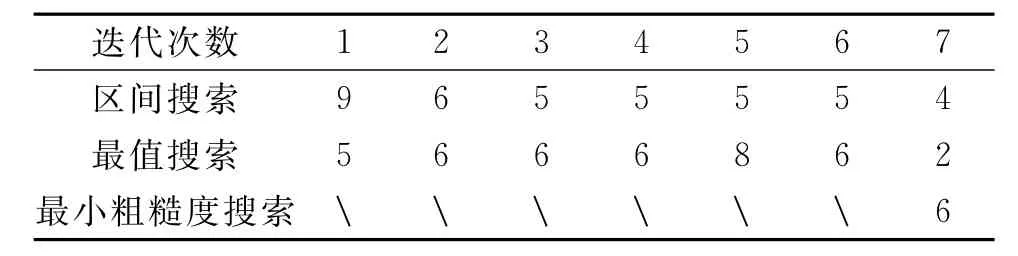
表3 模型1每次迭代自然二分法搜索次數Tab.3 The search process of each iteration of model 1by natural dichotomymethod

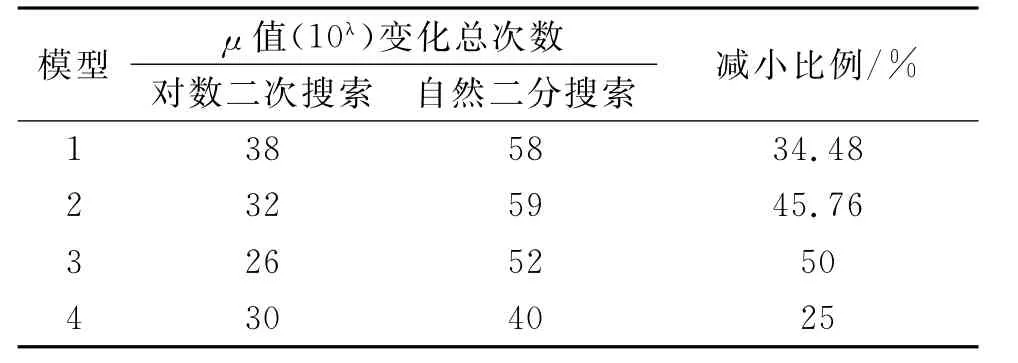
表4 四種模型μ值變化總次數對比Tab.4 The comparison of the number of Lagrange multiplier's search

4 結論

作者提出了一種Occam反演中拉格朗日乘子的搜索方法，此方法主要做了以下兩方面的改進。

1）利用關于拉格朗日乘子的絕對擬合誤差曲線的形態特征，用公式μ＝10λ對拉格朗日乘子做個變化，從而將對μ值的搜索變為對λ值的搜索，即將拉格朗日乘子的搜索從自然數域中轉化到了以10為底的對數域中進行。在運用過程中，發現對λ進行區間搜索的確很快，但也變相地加大了區間最小值的搜索范圍，在實際算例中，整體的搜索效率并沒有提高多少，故而進行了第二次改進。

2）利用區間搜索到的已知三點，構建關于λ值的擬合差二次函數，并求得此二次函數取得極小值時的λ值；用此λ值代入反演中求得擬合差，再得到一個新的谷值區間。這樣反復進行二次函數構建，尋找區間最小值。在實際算例中，我們發現往往只需要1次～3次二次函數構建就能搜索到區間的最小值，這大大地提高了區間最小值的搜索效率。

將以上兩種改進運用到拉格朗日乘子的搜索中，用模型算例驗證發現，此方法將搜索效率提高了20%～50%，大大減少了Occam法反演的運算時間。

本搜索方法僅僅在一維大地電磁反演中進行了驗證，有待在二維、三維中運用。

［1］ 石應駿，劉國棟，吳廣耀，等.大地電磁測深法教程［M］.北京：地展出版社，1985.

SHI Y J，LIU G D，WU G Y，Tutorial of MT sounding［M］.Beijing：Geological Publishing House，1985.（In Chinese）

［2］ 陳樂壽，劉任，王天生.大地電磁測深資料處理與解釋［M］.北京：石油工業出版社，1989.

CHEN L S，LIU R，WANG T S.Data processing and interpretation of MT sounding［M］.Beijing：Petroleum Industry Press，1989.（In Chinese）

［3］ 王家映.地球物理反演理論［M］.北京：高等教育出版社，2002.

WANG J Y.Inverse theory in geophysics［M］.Beijing：Higher Education Press，2002.（In Chinese）

［4］ CONSTABLE S C，PARKER R L，CONSTABLE C G.Occam's inversion：A practical algorithm for generating smooth models from electromagnetic sounding data［J］.Geophysics，1987，52（3）：289－300.

［5］ DEGROOT－HEDLIN C D，CONSTABLE S C.Occam's Inversion to Generate Smooth Two Dimensional Models form MagnetotelluricData［J］.Geophysics，1990，55（12）：1613－1624.

［6］ SIRIPUNVARAPORN W，EGBERTG.An efficient data－subspaceinversion method for 2－D magnetotelluricdata［J］.Geophysics，2000，65（3）：791－803.

［7］ SIRIPUNVARAPORN W，UYESHIMA M，EGBERT G.Three dimensional inversion for network－magnetotelluricdata［J］.Earth Planets Space，2004，56（9）：893－902.

［8］ RODI W L，MACKIE R L.Nonlinear conjugate gradients algorithm for 2－D magnetotelluricinversion［J］.Geophysics，2001，66（3）：174－187.

［9］ 韓波，胡祥云，何展祥，等.大地電磁反演方法的數學分類［J］.石油地球物理勘探，2012，47（1）：177－187.

HAN B，HU X Y，HE ZH X，et al.Mathematical classification of magnetotelluric inversion methods［J］.Oil Geophysical Prospecting，2012，47（1）：177－187.（In Chinese）

［10］陳小斌，趙國澤，湯吉，等.大地電磁自適應正則化反演算法［J］.地球物理學報，2005，48（4）：937－946.

CHEN X B，ZHAO G Z，TANG J，et al.An adaptive regularized inversion algorithm for magnetotelluric data ［J］.Chinese J Geophys，2005，48（4）：937－946.（In Chinese）

［11］吳小平，徐果明.大地電磁數據的OCCAM反演改進［J］.地球物理學報，1998，41（4）：547－554.

WU X P，XU G M.Improvement of OCCAM＇s inversion for MT date［J］.Chinese J Geophys，1998，41 （4）：547－554.（In Chinese）

［12］樸英哲，李桐林，劉永亮.在大地電磁二維Occam反演中求取拉格朗日乘子方法改進［J］.吉林大學學報：地球科學版，2014，44（2）：660－667.

PAK Y C，LI T L，LIU Y L.Improvement of choosing lagrange multiplier on MT 2DOccam inversion ［J］.Journal of Jilin University：Earth Science Edition，2014，44（2）：660－667.（In Chinese）

［13］劉俊峰，鄧居智，陳輝，等.一種用于Occam反演中搜索拉格朗日乘子的方法［J］.工程地球物理學報，2013，10（3）：344－350.

LIU J F，DENG J Z，CHEN H，et al.A method used for searching lagrange multiplier in Occam inversion ［J］.Chinese journal of engineering geophysics，2013，10（3）：344－350.（In Chinese）

Lagrange multiplier's search in one－dimensional magnetotelluric Occam's inversion

ZHANG Jun－tao1，ZHOU Jun1，WANG Xu－ben1，XIA Shi－bin1，ZHONG Hong－mei2
（1.Key Lab of Earth Exploration ＆information Techniques of Ministry of Education，Chengdu university of technology，Chengdu 610059，China；2.Sichuan Nuclear Industry Geological Survey Institute，Chengdu 610059，China）

In magnetotelluric inversion，because of its stability in inversion and the advantage of model resolution and so on，Occam method is widely used.But in each iteration，Occam＇s inversion needs to constantly search Lagrange multiplier.The searching efficiency of Lagrange multiplier to Occam＇s inversion speed plays a vital role.To improve the search efficiency of Lagrange multiplier，a new searching method was presented in this paper.First Lagrange multiplier of transfer from the natural number field to search for the 10logs base domain.Second in the search of interval minimum search method using quadratic function.Through a number of one－dimensional magnetotelluric inversions，Lagrange multiplier search efficiency is increased by 20%－50%，and the operation speed of Occam＇s inversion is greatly improved.

magnetotelluric；Occam inversion；Lagrange multiplier；logarithmic；quadratic function

P 631.3

：A

10.3969／j.issn.1001－1749.2015.06.03

1001－1749（2015）06－0687－06

2014－11－18改回日期：2014－12－14

地質調查項目（12120113095100）；重大儀器專項（2011YQ05006007）；四川省科技支撐計劃項目（2013FZ0084）；四川省教育廳項目（13ZB0062）

張君濤（1989－），男，碩士，主要研究方向為電磁法數據處理與正反演解釋，E－mail：Zjuntao＠foxmail.com。