雙足被動步行的全局穩定性分析

胡峻峰,曹 軍

(東北林業大學機電工程學院,哈爾濱150040)

雙足被動步行的全局穩定性分析

胡峻峰,曹 軍

(東北林業大學機電工程學院,哈爾濱150040)

在經典雙足被動步行動力學模型的基礎上,分析環境和力學參數影響下機器人被動步行的全局穩定性。計算不同模型參數下被動步行穩定不動點,采用胞胞映射計算得到不同模型參數下該動力學模型穩定單周期步態的吸引區域。研究發現雙足被動步行的魯棒性與其環境、力學參數關系密切,同時提出估計不動點吸引域形狀的2個度量:最小半徑與最大半徑。實驗結果給出被動步行穩定區域與斜坡傾角和質量比值的關系,同時通過分析某些偏離不動點較大的穩定吸引胞,以及吸引域的最小半徑與最大半徑的變化趨勢,反映了雙足被動步態的魯棒性。

雙足被動步行;全局穩定性;胞胞映射;不動點;吸引域;魯棒性

1 概述

傳統主動雙足機器人[1]盡管智能化程度高,能完成的動作多,可自主或受控改變行走速度和方向,但其結構復雜,步態顯得很機械,能量消耗大。雙足被動步行機器人充分利用自身機構固有的自然動力學特性,天生具有自然的步態,以及與人類步行相似的能量效率,迅速成為雙足機器人研究領域的一個嶄新且重要的分支。

經過近十年蓬勃發展,當前被動機器人在本體樣機設計和研制上種類繁多[2-3],但在行走穩定性方面仍無突破,具體體現在對行走初態的要求苛刻以及系統魯棒性很差,這與人類自然行走還有很大的差距[4-5]。雙足被動機器人要想取得進一步發展,就必須要研究雙足步行的內在固有特點,深入研究其控制與穩定性機理,雙足被動步行中的穩定性問題[6]主要分為步態局部穩定性與步態全局穩定性兩方面,作為雙足步行研究的基礎,其所得結論可以用來指導雙足機器人的設計和控制,實現降低控制器的復雜度和提高機器人整體能量效率。

目前被動行走步態的局部穩定性研究相對成熟,不動點的估計[7]與計算的數值方法[8]已經不少,但是步態的全局穩定性問題[9]研究有待深入,譬如應該如何衡量雙足被動機器人在不同參數下的全局穩定性的差異,從而選擇合適的參數來設計高效魯棒性好的被動機器人,另一方面,文獻[10]提出分域控制的思想,通過進一步分析機器人的穩定行走的吸引區域,有利于提出高效的全局穩定分域控制切換邏輯。文獻[11]等使用胞胞映射定性地刻畫出相應被動步行模型的穩定不動點的吸引區域[12]的形狀和體積,從而反映在不同參數下滿足能讓被動機器人穩定行走的初始條件集合的變化情況[13],但是上述吸引區域及機器人在相應模型下的全局穩定性[14]需要進行分析并提取特征。因此,本文通過數值研究,分析討論在不同環境與力學參數影響下雙足被動步行穩定步態[15]吸引區域的差異及演化規律。

2 預備知識

2.1 雙足被動步行的動力學建模

將文獻[14]的無膝雙足被動行走模型作為研究對象,其2條均質剛性直腿有完全相同的質量與幾何參數,直腿質心處集中了腿上所有質量,同時髖關節處具有質量,如圖1所示。

圖1 斜坡上的雙足被動步行動力學模型

其中:

在擺動腿觸地瞬間,系統的支撐腿與擺動腿發生互換,狀態變量發生突變,假設碰撞時間極短且為完全非彈性碰撞,易知在碰撞瞬間雙腳都著地,兩腿角度滿足如下關系式:

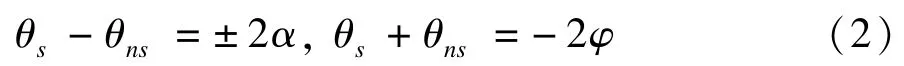
根據角動量守恒原理,在碰撞時刻T前后的狀態變量滿足如下代數方程:

2.2 步態的穩定性分析與計算

文獻[5]首先定義并研究了步態的局部穩定性,自其開創性工作以來,研究者一般首先建立步態方程,然后沿用Newton-Raphson方法[5]在預先估計的狀態空間里搜索系統的穩定周期解。通過類似方法,建立上述模型的步態方程,見式(1)與式(3),然后以雙足著地的碰撞瞬間作為Poincare截面,根據式(2),則2次碰撞之間的過程是一個三維Poincaré映射F,其狀態變量Xi∈R3,i=1,2,…,n,可知Xi+1=F(Xi),若F(X?)=X?,則周期步態存在,此時龐加萊映射的固定點X?稱為不動點,以穩定的不動點作為步態初值,機器人行走會呈周期步態。然而機器人具有局部穩定性,僅能說明機器人可以形成穩定的行走狀態,而機器人行走的初始條件偏離其穩定不動點多大范圍內仍能形成穩定行走狀態,需要對其進行全局穩定性分析。全局穩定性越好,魯棒性越好,滿足穩定行走的初始條件的范圍越大,被動機器人穩定行走抗干擾的能力就越強。滿足能讓被動機器人形成穩定步態的集合稱為不動點的吸引域,把吸引域內的點作為雙足被動步行機器人的初始條件,經過有限步運動以后都將收斂到穩定運動狀態。因此,可以用吸引域的大小等特征來分析雙足被動機器人的全局穩定性。

文獻[12]在上述局部穩定性研究方法上進行了擴展,采用胞胞映射方法在Poincaré像空間上找到不動點的吸引域。為了衡量雙足被動步行系統在不同參數下的魯棒性以及給后續控制算法提供理論支持,定義吸引域最小半徑Rmin與最大半徑Rmax。

設在Poincaré像空間上取一初始狀態集S,Σ是其內部穩定不動點的吸引點集,易知Σ?S,將任意點Y與穩定不動點Y0之間的距離定義為d=Y-Y0,S中任意滿足d≤Smin的初始狀態變量Y都能收斂到穩定不動點上。在初始狀態空間中滿足d＞Smax的任意初始狀態變量Y肯定無法收斂到穩定不動點上。可見,吸引域最小半徑Smin反映了雙足被動機器人在初始狀態偏離不動點多大程度時經過有限步以后必定可以回到單周期穩定步態。

而吸引域最大半徑Smax反映了機器人在初始狀態偏離不動點多大程度時仍舊有可能經過有限步回到單周期穩定步態。

3 數值實驗與分析

3.1 實驗環境

文獻[10]中發現,被動步行行走過程對環境擾動的魯棒性是由機器人的力學參數和斜面坡度共同決定。下面分析質量參數μ,斜面坡度φ的變化對穩定不動點吸引域的影響。

3.2 參數μ對穩定步態吸引域的影響

采用前述Newton-Raphson迭代方法求取了μ=1∶ 0.1∶10下的穩定不動點變化情況,在參數連續變化時,系統的穩定不動點的變化也是連續的,而且隨參數μ的增大,穩定不動點的變化越來越小,如圖2所示。

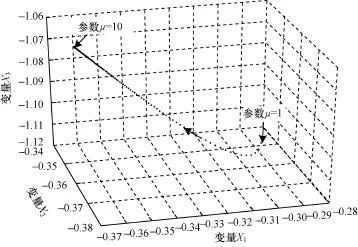
圖2 參數μ從1增加到10時的系統穩定不動點

在上述胞化的初始狀態空間里,利用胞映射法求取了不同的參數μ下吸引到其對應的穩定不動點的初始狀態胞,其中,μ=1,2,4,6,8下的吸引域如圖3所示。

圖3 隨參數μ從1～10變化時穩定不動點的吸引域

如圖3所示,隨參數μ的增大,穩定不動點的吸引域的體積在μ=3時明顯變大,然后繼續變大,可見雙足被動機器人的髖關節重量相對腿重量越大,其魯棒性越好,而且在比值大約為3時,其穩定性區域就可以達到較理想的程度,這與人類身體結構重量分配的常識也是一致的。在圖中取μ=1時的不動點的吸引區域一遠端點Ym=[0.696 39, -2.932 5,2.812 5],對其進行迭代,發現其在迭代次數n≤20時就可以迅速收斂到不動點Y0= [-0.295 69,-0.362 84,-1.1063],如表1所示。

表1 吸引點Ym的收斂情況

由表1可知,如果雙足被動機器人的初態哪怕偏離穩定步態很遠,如果合適的話,恢復到穩定狀態的過渡時間T與狀態偏差d收斂很快,因此,可以迅速回到穩定的單周期步態。通過觀察圖3發現,這樣的點與擺動腿角速度的正負有關系,如果擺動腿的角速度為正,且足夠大的話,那系統就有足夠的機會回到穩定步態。隨后,估算隨參數μ變化,穩定不動點吸引域的最小半徑與最大半徑如圖4所示。

圖4 吸引域的最小半徑與最大半徑

由圖4可知,在參數μ增加時,雙足被動步行機器人的魯棒性越來越好,在μ≈7時,步行機器人肯定可以承受最大偏離程度的擾動,但是此時最大半徑較小,如果偏離較大,需要消耗更多能量鎮定到離其最近可以調整到穩定步態的狀態上。而在參數μ≈2時,即使步行機器人受到的擾動較大,但是仍舊在最大半徑所包含的范圍內,僅需少許能量就可以將其狀態鎮定到距離其最近的吸引點上,因此,有利于工程實現與設計。

3.3 斜坡傾角φ對穩定步態吸引域的影響

采用前述Newton-Raphson迭代方法求取了φ= 0.25°∶0.25°∶4°下的穩定不動點的變化情況,由圖5可知,隨傾角變化,穩定不動點在相空間中的變化也是連續的。

圖5 參數φ從1增加到10時的系統穩定不動點

在上述胞化的初始狀態空間里,利用胞映射法求取了不同斜坡傾角φ下吸引到其對應的穩定不動點的初始狀態胞,其中,φ=0.25°,1°,2°,3°,4°下的吸引域如圖6所示。從圖6可以看出,隨傾角φ的增大,穩定不動點的吸引域的體積在φ=3時明顯變大,然后繼續變大,可見斜坡傾角在合適的范圍內相對較大時,雙足被動機器人的魯棒性更好,而且在比值大約為3時,其穩定性區域就可以達到較理想的程度。

隨后,也同時估算了隨傾角φ變化,穩定不動點吸引域的最小半徑與最大半徑,如圖7所示。

圖6 隨參數φ從0.25°到4°變化時穩定不動點的吸引域

圖7 吸引域的最小半徑與最大半徑

可知在斜坡傾角φ增加時,雙足被動步行機器人的吸引區域越來越大,隨斜坡傾角的增大,其吸引域的最大半徑與最小半徑增長較快,系統的魯棒性越來越好,但是斜坡傾角大于5.07°時會出現復雜的動力學現象[14],如倍周期分岔、混沌等。

4 結束語

本文使用數值方法對不同環境與力學參數下雙足被動行走模型的全局穩定性進行了研究與討論。研究發現,雙足被動步行的魯棒性與其環境、力學參數關系密切,同時提出估算其不動點的吸引區域的最小半徑與最大半徑對后續的工程設計以及控制策略提供支持,如在環境參數給定的情形下,設計具備與它匹配的力學參數的機器人以獲得最大的吸引區域,同時在評估當前控制策略設計是否合理時應該著重考慮2個關鍵性度量,即吸引區域最小半徑與最大半徑。下一步工作主要集中在如何高效且精確地計算其不動點的吸引區域以及能量問題。

[1] Sakagami Y,Watanabe R.The Intelligent ASI-MO:System OverviewandIntegration[C]//Proceedingsof InternationalConferenceonIntelligentRobotsand Systems.Piscataway,USA:IEEE Press,2002:2478-2483.

[2] Wisse M.Three Additions to Passive Dynamic Walking; Actuation,an Upper Body,and 3D Stability[C]// Proceedings of International Conference on Humanoid Robots.New York,USA:IEEE Press,2004:113-132.

[3] Collins S H,Ruina A.A Bipedal Walking Robot with Efficient and Human-like Gait[C]//Proceedings of Conference on Robotics and Automation.Piscataway, USA:IEEE Press,2005:1983-1988.

[4] Tedrake R.Stochastic Policy Gradient Reinforcement Learning on a Simple 3D Biped[C]//Proceedings of InternationalConferenceonIntelligentRobotsand Systems.NewYork,USA:IEEEPress,2004: 2849-2854.

[5] McGeer T.Passive Dynamic Walking[J].International Journal of Robotics Research,1990,9(2):62-82.

[6] 毛 勇,王家廒,賈培發,等.雙足被動步行研究綜述[J].機器人,2007,29(3):274-280.

[7] 蘇學敏,趙明國,張 楫,等.被動行走周期性步態不動點搜索的新算法[J].清華大學學報:自然科學版, 2009,49(8):1109-1112.

[8] 柳 寧.雙足模型步行中的倍周期步態和混沌步態現象[J].物理學報,2009,58(6):3772-3779.

[9] 倪修華,陳維山.基于BP神經網絡的被動步行穩定不動點的估算[J].機器人,2010,32(4):478-483.

[10] Spong M W.Passivity Based Control.of the Compass Gait Biped[C]//Proceedings of IFAC World Congress. Amsterdam,the Netherlands:Elsevier Science Ltd., 1999:19-23.

[11] 曲俊法,雙足被動步行機器人行走穩定性的研究[D].哈爾濱:哈爾濱工業大學,2008.

[12] Wisse M,Frankenhuyzen J.Design and Construction of Mike,A 2d AutonomousBipedBasedonPassive Dynamic Walking[C]//Proceedings of Conference on Adaptive Motion of Animals and Machines.Kyoto, Japan:[s.n.],2003.

[13] 柳 寧,李俊峰.用胞胞映射計算被動行走模型不動點的吸引盆[J].工程力學,2008,25(10):218-223.

[14] Goswami A,Thuilot B,Espiau B.Compass-like Biped Robot PartI:StabilityandBifurcationofPassive Gaits[R].HondaResearchInstituteUSA,Inc., Technical Report:INRIA 2996,1996.

[15] 胡運富.無膝雙足被動機器人的運動特性和穩定性研究[D].哈爾濱:哈爾濱工業大學,2009.

編輯 顧逸斐

Analysis for Global Stability of Passive Bipeds Walking

HU Junfeng,CAO Jun
(College of Mechanical and Electrical Engineering,Northeast Forest University,Harbin150040,China)

Based on the classical dynamic model of passive biped walking,the globel stability of passive bipeds walking which is influenced by the environment and mechical parameters is discussed.The calculaion about stable fix points on variable parameter is given.Cell-cell map is used to compute the attractive region of the1-periodic steady gait of the walking model with variable parameters.It is found that the robustness of passive bipeds is connected closely to the environment and mechanical parameters.Moreover,this paper also proposes the two metrics to evaluate the shape of attractive region:minimum radius and maximum radius.Simulation results also reveal the relationship between the attractive region of passive walking and the parameters like ground slope or mass ratio.Simultaneously,the robusness of passive biped walking gaits is analyized by special attracive cell and the variable tendency with the maximum reach and the mininum reach of the attractive region.

passive bipeds walking;global stability;cell-cell mapping;fix point;attractive region;robustness

胡峻峰,曹 軍.雙足被動步行的全局穩定性分析[J].計算機工程,2015,41(2):173-177.

英文引用格式:Hu Junfeng,Cao Jun.Analysis for Global Stability of Passive Bipeds Walking[J].Computer Engineering, 2015,41(2):173-177.

1000-3428(2015)02-0173-05

:A

:TP39

10.3969/j.issn.1000-3428.2015.02.033

中央高校基本科研業務費專項基金資助項目(DL10AB06);國家林業局“948”基金資助項目(2011-4-04);黑龍江省自然科學基金資助項目(QC2012C101)。

胡峻峰(1980-),男,博士研究生,主研方向:人工智能,圖像處理;曹 軍,教授、博士、博士生導師。

2013-10-08

:2013-12-27E-mail:hujunfeng_2013@126.com