雙索同時張拉無應力狀態(tài)控制方法模型研究

楊 春

（上海浦東建筑設計研究院有限公司,上海市 201204）

0 引言

無應力狀態(tài)控制方法是秦順全[1]提出的一種解決橋梁施工控制的理論方法。這種控制方法基于兩個最重要的基本原理[2]，其一，一定的結(jié)構(gòu)體系、邊界條件、外荷載和無應力狀態(tài)量唯一決定了結(jié)構(gòu)的內(nèi)力和變形，只要上述4個條件不變，結(jié)構(gòu)的內(nèi)力、變形與安裝成形過程無關(guān)；其二，無應力狀態(tài)量不隨其余3個條件的變化而變化，只在自身調(diào)整時才會變化。結(jié)構(gòu)的無應力狀態(tài)量是施工過程中眾多參量中穩(wěn)定的控制量[3]，是無應力狀態(tài)控制法的核心。無應力狀態(tài)控制方法實現(xiàn)了分階段施工控制中對溫度、臨時荷載影響的自動過濾[4]，同時能解決并行作業(yè)的施工控制問題[5]。該方法不僅在多種橋型的施工過程中成功運用[6～13]，而且還被用于一些特殊的施工工藝[14～15]。

斜拉橋的無應力狀態(tài)量主要有斜拉索的無應力長度和主梁的無應力曲率。其中，主梁無應力曲率很難在施工過程中進行調(diào)節(jié)，一般通過調(diào)整索力和加臨時配重的方式使主梁平順合攏得以實現(xiàn)，合攏后再不能對主梁無應力曲率進行調(diào)整，而斜拉索無應力長度則能在任意階段進行調(diào)整。因此，斜拉橋施工過程的無應力狀態(tài)控制主要是對斜拉索無應力長度進行控制。在已有的文獻中，關(guān)于斜拉索無應力長度控制的理論模型只限于單索張拉，然而在實際施工中，通常要求對稱張拉斜拉索，單索理論并不適用多索同時張拉的情況。針對這個問題，本文將在單索理論的基礎上提出雙索同時張拉的一般理論模型，并對模型參數(shù)的取值進行討論。

1 模型建立

斜拉橋的雙索同時張拉模型如圖1所示。其中，用M表示斜拉索主梁張拉端，N表示斜拉索主塔張拉端，主梁彈性剛度分別為KM1和KM2，主塔彈性剛度為KN，1#和2#索的彈性模量分別為E1和E2、截面面積分別為A1和A2，1#和2#索的張力分別為T1和T2、無應力長度分別為L10和L20，塔、梁間的無應力距離為S。

圖1 雙索模型示意圖

在初始平衡狀態(tài)下，斜拉索的有應力長度與塔、梁變形量之和等于塔、梁間無應力距離，其幾何變形協(xié)調(diào)關(guān)系如下：

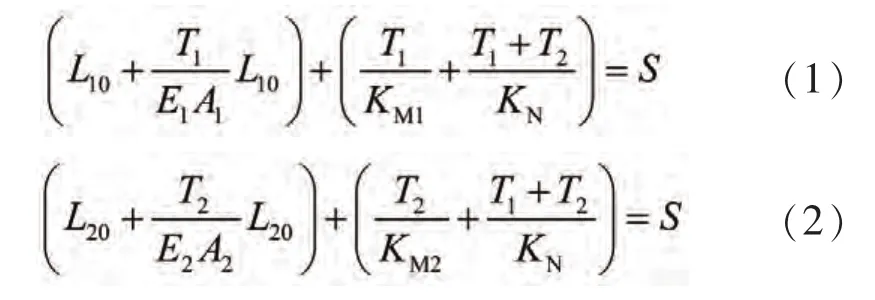
通過千斤頂主動調(diào)整1#和2#索的張拉力，調(diào)整量分別為△T1和△T2，調(diào)整后的無應力長度分別為L'10和L'20，在新平衡狀態(tài)下的幾何變形協(xié)調(diào)關(guān)系如下：

將式（3）-式（1）、式（4）-（2），并忽略二階小量得：

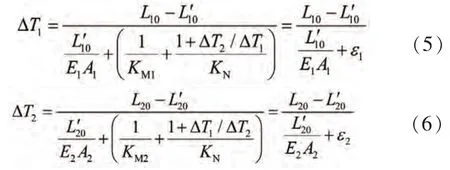
式中：ε1為1#索施加單位張力、2#索施加張力△T2/△T1時，沿1#索方向塔、梁距離的變化量；ε2為2#索施加單位張力、1#索施加張力△T1/△T2時，沿2#索方向塔、梁距離的變化量。

2 關(guān)鍵參數(shù)討論

式（5）和式（6）表明在結(jié)構(gòu)體系、外荷載不變時，斜拉索無應力長度調(diào)整量與索力調(diào)整量存在一一對應關(guān)系。但在雙索同時張拉時，式（5）和式（6）相互耦合，無法直接進行計算。下面對式（5）和式（6）中參數(shù)ε的幾種取值情況進行討論。

（1）大多數(shù)斜拉橋采用對稱懸臂方式施工，斜拉索對稱張拉，若在懸臂階段需要對稱調(diào)整索力，那么有△T1=△T2，于是，式（5）、式（6）可以簡化為：

（2）對于雙索非對稱調(diào)整索力的情況，可先假設△T1=△T2，代入式（5）和（6）分別計算出△T1和△T2，如此循環(huán)迭代，直至滿足收斂要求，即可得到相應的非對稱索力調(diào)整量。

（3）主梁合攏后，索力往往不再需要進行對稱調(diào)整，更多的是對單索進行調(diào)整，這種情況下式（5）和式（6）就退化為單索模型，即：

（4）對于在主梁跨中區(qū)域錨固的長索，單位索力作用下索塔的彈性變形遠小于主梁彈性變形，因此可忽略索塔變形對參數(shù)ε的影響，于是式（5）和式（6）可解耦成獨立的單索模型，即：

（5）對每根索而言，剛度KM、KN在懸臂施工階段與主梁合攏后是不相同的，具體的取值根據(jù)索力調(diào)整時的結(jié)構(gòu)體系而定。

3 算例驗證

為了驗證上述雙索模型的正確性，下面以一座假想的三跨斜拉橋作為算例，如圖2所示。該斜拉橋計算模型采用塔梁墩固結(jié)體系，中跨35 m，邊跨20 m，塔高20 m，墩高5 m，梁端索距5 m，墩與塔截面1 m×1 m，主梁截面0.5 m×0.5 m，索截面直徑0.01 m，塔梁墩材料C50，索材料Q345，不計墩與塔結(jié)構(gòu)自重，假定主梁自重80kN/m。斜拉索編號由邊跨到中跨分別為 3#、2#、1#、4#、5#、6#。

圖2 三跨斜拉橋算例有限元模型示意圖

該斜拉橋的目標成橋狀態(tài)按先梁后索的施工方式優(yōu)化索力得到，實際施工正裝分析計算按懸臂施工方式進行。斜拉索的初張力可隨意指定，在該模型中短索到長索的初張力分別為250 kN、250 kN、200 kN。主梁合攏時采用施加臨時配重方式使得主梁平順合攏。主梁合攏后再將每根索的無應力長度調(diào)至目標成橋狀態(tài)，調(diào)索按1#與4#、2#與5#、3#與6#的組合方式依次進行。該 算例的計算分析采用通用有限元軟件平臺Midas Civil，施工過程計算考慮結(jié)構(gòu)的幾何非線性，這樣計算的結(jié)構(gòu)受力過程更符合真實情況。

斜拉索目標成橋狀態(tài)、初張拉和調(diào)索后的索力、無應力長度，以及調(diào)索時的ε值計算結(jié)果見表1所列。主梁目標成橋狀態(tài)和調(diào)索后的彎矩分別如圖3和圖4所示，圖中索間梁段彎矩圖未出現(xiàn)下彎，是因為Midas非線性分析時只輸出單元節(jié)點的計算結(jié)果，不輸出單元內(nèi)部的插值結(jié)果。通過比較目標成橋狀態(tài)與調(diào)索后的索力、無應力長度和主梁彎矩，可以看出：

表1 三種狀態(tài)下的索力及其無應力長度一覽表

圖3 主梁目標成橋彎矩圖（單位：kN·m）

圖4 主梁調(diào)索后彎矩圖（單位：kN·m）

（1）調(diào)索后的索力、無應力長度與目標成橋狀態(tài)非常接近，主梁彎矩分布趨勢也一致，但存在較小的差異，說明本文提出的雙索同時張拉無應力狀態(tài)控制模型是正確的。

（2）調(diào)索后的索力均偏小，無應力索長均偏大。出現(xiàn)這種差異主要有兩個原因：一是該算例中的塔、梁的長細比較大，且承受的軸壓力也較大，在這種情況下，塔、梁的幾何非線性比較顯著，剛度出現(xiàn)明顯的軟化現(xiàn)象，而式（5）和式（6）是在彈性理論基礎上建立的，其計算出的ΔT值會偏小；二是懸臂和先梁后索兩種施工成形的主梁無應力梁長會有差異，在施工過程模擬中未對無應力梁長做調(diào)整，這必然會對兩種方式的成橋內(nèi)力帶來差異。

4 結(jié)語

（1）本文在單索無應力狀態(tài)控制模型的基礎上提出了雙索同時張拉的無應力狀態(tài)控制理論模型。研究發(fā)現(xiàn)雙索同時張拉模型的無應力長度調(diào)整量與索力調(diào)整量依然存在一一對應關(guān)系，只是兩索之間相互耦合，這可以通過迭代求解方式得以解決。通過對各種情況下關(guān)鍵參數(shù)ε取值的討論，發(fā)現(xiàn)雙索模型實際上包含單索模型，在索塔剛度遠大于主梁剛度的情況系下，可以近似解耦成兩個獨立的單索模型。對于多索同時張拉的情況，完全可以在本文思路的基礎上加以拓展。

（2）以一座假想的三跨斜拉橋為例，驗證了本文雙索模型的正確性。計算結(jié)果表明，即使在幾何非線性比較顯著的情況下，雙索模型依然能得到可靠的無應力長度調(diào)整量。

[1]秦順全,林國雄.斜拉橋安裝計算——倒拆法與無應力狀態(tài)控制法評述[A].1992年全國橋梁結(jié)構(gòu)學術(shù)大會論文集[C].上海:同濟大學出版社,1992:569-573.

[2]秦順全.分階段成形結(jié)構(gòu)過程控制的無應力狀態(tài)控制法[J].中國工程科學,2009,(10):72-78.

[3]秦順全.斜拉橋安裝無應力狀態(tài)控制法[J].橋梁建設,2003,（2）：31-34.

[4]秦順全.分階段施工橋梁的無應力狀態(tài)控制法[J].橋梁建設,2008,（1）:8-14.

[5]萬淑敏.無應力狀態(tài)控制法在斜拉橋并行作業(yè)中的應用[J].世界橋梁,2012,（4）:59-63.

[6]秦順全.橋梁施工控制——無應力狀態(tài)法理論與實踐[M].北京:人民交通出版社,2007.

[7]靳國勝.無應力狀態(tài)施工控制法在松花江斜拉橋的應用[J].山西建筑,2007,（9）:324-325.

[8]李斌.無應力狀態(tài)法在結(jié)合梁斜拉橋施工控制中的應用[D].成都:西南交通大學,2010.

[9]吳運宏,岳青,江湧，等.基于無應力狀態(tài)法的鋼箱梁斜拉橋成橋目標線形的實現(xiàn)[J].橋梁建設,2012,42(5):63-68.

[10]白絮.基于無應力狀態(tài)法的無背索斜拉橋施工控制[D].西安:長安大學,2012.

[11]劉建.鋼管混凝土拱橋無應力狀態(tài)法施工控制研究[D].成都:西南交通大學,2013.

[12]秦順全.無應力狀態(tài)控制法——斜拉橋安裝計算的應用[J].橋梁建設,2008,（2）:13-16.

[13]劉小剛.無應力狀態(tài)法在鋼桁梁斜拉橋施工控制中的應用[D].廣州:華南理工大學,2012.

[14]李文武,潘勝山,張哲,葉毅.無應力狀態(tài)有限元法在橋梁豎轉(zhuǎn)施工中的應用[J].武漢理工大學學報,2010,32(21):46-50.

[15]苑仁安,秦順全.無應力狀態(tài)法在鋼絞線斜拉索施工中的應用[J].橋梁建設,2012,42(3):75-79.