基于低秩表示中稀疏誤差的可變光照和局部遮擋人臉識別*

楊國亮，豐義琴，魯海榮

(江西理工大學電氣工程與自動化學院，江西 贛州 341000)

基于低秩表示中稀疏誤差的可變光照和局部遮擋人臉識別*

楊國亮，豐義琴，魯海榮

(江西理工大學電氣工程與自動化學院，江西 贛州 341000)

可變光照和有遮擋人臉識別是人臉識別問題中的一個難點。受到魯棒主成分分析法(RPCA)和稀疏表示分類法(SRC)的啟發，提出一種基于低秩表示(LRR)中稀疏誤差圖像的可變光照有遮擋人臉識別算法。在訓練階段，利用LRR計算每類人臉低秩數據矩陣，在此基礎上求解每類人臉圖像低秩映射矩陣，通過各類低秩映射矩陣將未知人臉圖像投影得到每類下的低秩數據矩陣和稀疏誤差矩陣，為了有效提取稀疏誤差圖像中的鑒別信息，分別對稀疏誤差圖像進行邊緣檢測和平滑度分析，設計了基于兩者加權和的類別判據。在Extended Yale B和AR兩個數據庫上進行了詳細的實驗分析，實驗結果與其它算法相比較有明顯提高，證實了所提算法的有效性和魯棒性。

低秩表示；低秩映射；稀疏誤差圖；人臉識別

1 引言

由于受到光照和局部遮擋等因子的影響，傳統的人臉識別方法受到實用性的考驗。最近幾年已經有很多的專家學者開始致力于帶光照變化以及局部遮擋的人臉識別研究。主成分分析法PCA(Principal Component Analysis)是將高維數據提取主要特征后實現有效降維。PCA方法對于數據中幅值小的噪聲具有較好的魯棒性，當噪聲幅值較大時，算法性能嚴重下降。Candès E[1]和Wright J[2]提出的魯棒主成分分析法RPCA(Robust Principal Component Analysis)對具有較大幅值的稀疏誤差具有較好的恢復效果，RPCA方法是將數據矩陣分解成低秩矩陣和稀疏噪聲兩部分，在數據受到較大污染的情況下也能在一定程度上比較好地實現低秩矩陣恢復，具有較強的魯棒性，因而受到機器視覺領域的廣泛關注。

Wright J等人[3]在2009年提出基于Lasso回歸的稀疏表示分類器方法SRC(Sparse Represenlation_based Classificaton)。SRC是將人臉識別問題看作是多元線性回歸模型中的分類問題，將測試的人臉圖像表示成所有訓練圖像的線性組合，然后利用重構樣本和測試樣本間的殘差來判斷測試樣本所屬的類別。針對SRC對連續遮擋情況下的魯棒性減弱問題，Naseem I等人[4]提出了線性回歸分類器方法LRC(Linear Regression Classification)。LRC是將人臉識別問題看作線性回歸問題，對于每一類的所有訓練樣本都采用最小二乘估計，然后對測試圖像進行擬合。該方法充分考慮了殘差圖像的稀疏特性，此外，SRC和LRC在處理人臉光照問題上具有較好的效果。

受到RPCA和SRC及LRC方法的啟發，本文采用最新的低秩表示模型LRR(Low Rank Representation)將數據矩陣分解為低秩數據矩陣和稀疏噪聲兩部分，與RPCA不同的是，LRR[5,6]是假設對于某個字典，數據集的表示系數是低秩的，旨在尋求數據矩陣的最低秩表示。本文使用LRR對每一類的訓練樣本進行分解，得到低秩矩陣與稀疏矩陣和的形式。由于遮擋部分在誤差圖像中特征比較顯著，使得稀疏誤差圖像不僅包含了類內信息，而且包含了類間信息，其中類間信息對分類起著關鍵作用。為了避免對每個測試樣本都進行LRR分解，本文先利用LRR模型計算每類的低秩映射矩陣，即通過LRR模型對每類樣本分別計算其低秩數據矩陣，建立每類原始樣本與低秩數據樣本之間的低秩映射關系(低秩映射矩陣)；然后將測試樣本在每類低秩映射矩陣下進行投影，從而可以得到一系列稀疏誤差圖像。為了充分提取稀疏誤差圖的鑒別信息，使用邊緣檢測刻畫稀疏誤差圖像的局部邊緣信息，同時使用平滑度分析方法獲取整體誤差圖像的全局梯度信息，采用邊緣信息和平滑度信息的加權和對人臉圖像進行分類。

2 基于稀疏誤差圖像的可變光照和局部遮擋人臉識別算法

針對可變光照和有遮擋人臉識別問題，借鑒低秩建模理論，本文提出了一種基于低秩表示模型中稀疏誤差圖像的魯棒人臉識別算法，其主要步驟為：(1)對每類訓練人臉利用LRR模型計算低秩數據矩陣，建立低秩數據矩陣與原始訓練樣本之間的低秩映射關系，得到每類人臉圖像的低秩映射矩陣；(2)利用各類低秩投影矩陣計算測試樣本對應的低秩數據矩陣，進而得到測試樣本對應的稀疏誤差圖像；(3)對稀疏誤差圖像進行邊緣檢測和平滑度分析，提取稀疏誤差圖像中的鑒別信息；(4)采用邊緣信息與平滑度信息加權和作為人臉識別依據。具體的算法框架如圖1所示。

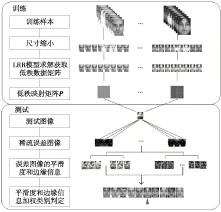
Figure 1 Framework of the proposed method

2.1 低秩表示

對訓練樣本數據集X=[x1,x2,…,xn]∈Rd×n，構造一個字典A=[a1,a2,…,am]∈Rd×m，使得X=AZ,其中Z是表示系數矩陣，Z=[z1,z2,…,zn]。一般情況下字典A都是過完備的，這就使得Z有很多個解，而低秩表示的目的則是為了尋找其最低秩解，即尋找一個最低秩的Z。一般地，為了簡化模型結構，多選用數據矩陣本身來構造字典。問題轉化為如下模型的求解：

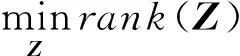
s.t. X=XZ

(1)

由于直接求解矩陣的秩是一個NP難問題，Candès E等人[1]提出使用核范數替代矩陣的秩，并證實了該方法的有效性。因此，問題(1)可以轉變成如下凸優化問題：

s.t. X=XZ

(2)

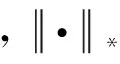
s.t. X=XZ+E

(3)

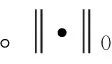
s.t. X=XZ+E

(4)

對于問題(4)的求解，文獻[8]詳述了比較多的求解算法，本文采用非精確增廣拉格朗日乘子法IALM(Inexact Augmented Lagrange Multiplier)。為降低模型計算難度，參照文獻[9,10],引入輔助變量J，模型轉化為：

s.t. X=XZ+E,Z=J

(5)

其所構建的增廣拉格朗日函數如下:

(6)

(7)

(8)

(I+XTX)-1(XTX-XTEk+1+Jk+1+

(XTY1,k-Y2,k)/μk)

(9)

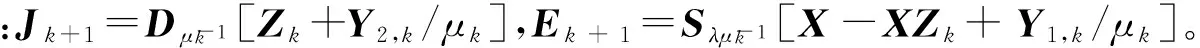
使用IALM法分別對拉格朗日函數中的每個變量進行交替迭代尋優，具體實現步驟如算法1所示。

算法1使用IALM算法求解低秩表示模型

輸入：數據矩陣X∈Rd×n，參數λ;

輸出：Z*，E*。

初始化：Z0=J0=E0=0，Y1,0=Y2,0=0,μ0=10-6,μmax=1030,ρ=1.1,ε=10-8；

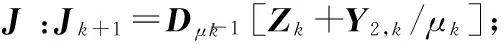
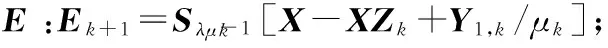
3.更新Z: Zk+1=(I+XTX)-1(XTX-XTEk+1+Jk+1+(XTY1,k-Y2,k)/μk);

4.更新乘子Y1,Y2:Y1,k+1=Y1,k+μk(X-XZk+1-Ek+1),Y2,k+1=Y2,k+μk(Zk+1-Jk+1);

5.更新μ：μk+1=min(ρμk,μmax) ;

6.更新k：k←k+1;

End while

2.2 低秩映射矩陣

對于任意輸入的一張測試圖片，無法判定其具體所屬的類別，又由于遮擋部分在誤差圖像中特征顯著，為了獲得實用有效的稀疏誤差圖，在對每一類的訓練樣本數據進行LRR模型求解獲取低秩數據矩陣后，在訓練樣本數據與低秩數據之間建立低秩映射。獲取低秩映射矩陣的過程是一個離線的過程，這樣，在對人臉的測試過程中，只需要將測試人臉圖像在每一類的低秩映射矩陣上進行映射，再與原圖作差即可獲得相應的稀疏誤差圖像，在一定程度上減少了計算復雜度，節約了測試時間。

關于低秩映射矩陣P的獲取，算法描述為：假定有一個訓練樣本X=[X1,X2,…,XN]∈RM×L，M=m×n為每一張訓練圖像的大小，N為訓練的所有類別數,L為整個訓練樣本中圖像的總數。對于第i類訓練樣本數據Xi,i∈(1,N)，根據算法1求解低秩表示模型，獲得對應的一組(Zi,Ei)，從而計算出該類訓練樣本數據的低秩部分數據矩陣Yi=XiZi，為了計算實際測試人臉圖像在每類上對應的低秩數據矩陣，必須通過X和Y對低秩映射矩陣P進行學習。對于每一類(Xi,Yi),可以找到一個潛在的低秩映射矩陣Pi，使得PiXi=Yi。對于低秩映射矩陣Pi的求解可以轉化為模型(10)的優化問題：

s.t. Yi=PiXi

(10)

對問題(10)進行凸優化，轉化成對問題(11)的求解：

s.t. Yi=PiXi

(11)

算法2基于低秩表示求解低秩映射

輸入：第i類訓練樣本數據Xi,i∈(1,N);

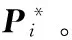
1.求解LRR模型，獲取低秩表示Zi;

2.計算低秩數據矩陣Yi：Yi=XiZi;

3.構建低秩映射關系：PiXi=Yi;

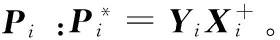
2.3 稀疏誤差圖分析

本文算法中，在訓練部分對每一類的訓練樣本數據使用算法2獲得其對應低秩映射矩陣Pi。在測試部分，數據庫中任意給定的一張測試圖片y，都可以通過Pi在第i類訓練樣本上獲得相應的低秩數據圖，然后將測試樣本與低秩數據圖作差便可獲得稀疏誤差圖，即對于每一個輸入的測試樣本將通過低秩映射矩陣P產生與總類別數相同的稀疏誤差圖。

為了更好地提取稀疏誤差圖的類別信息，首先想到的是使用基于Sobel算子的邊緣檢測來刻畫，然而邊緣檢測方法只能獲取稀疏誤差圖的局部邊緣信息，缺乏對全局信息的提取，進而加入對誤差圖求導的平滑度分析方法，從梯度的角度獲取誤差圖全局梯度信息。本文在3.1節和3.3節分別進行了只提取邊緣信息和同時提取邊緣與平滑度信息作為鑒別信息并進行了實驗分析。

圖2為同一張測試圖像在不同的類上所獲取的稀疏誤差圖，以及對應的平滑度圖和邊緣信息圖，圖2b～圖2d中的第一張圖分別為正確類產生的稀疏誤差圖、邊緣信息圖以及平滑度圖。

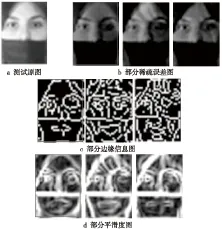
Figure 2 Images of a test sample

從圖2c中可以直觀地了解到，在正確類所對應的邊緣信息圖中的邊緣線明顯比非正確類的邊緣線少；在圖2d中可以看出，正確類對應的平滑度圖表現得更加平滑。無論是平滑度圖還是邊緣信息圖都顯示，正確類對應的稀疏誤差圖與非正確類對應的稀疏誤差圖存在明顯區別，這些信息刻畫了樣本的類間差異，可以作為分類的判斷依據。

為了更好地進行描述，定義兩個描述子：平滑度描述子Dsmooth和邊緣信息描述子Dedge。

(12)

其中，ex和ey分別表示稀疏誤差圖像在x方向和y方向上的梯度，BW為稀疏誤差圖像的邊緣檢測后的二值圖像。

選擇對圍巾遮擋下的不同稀疏誤差圖分別進行邊緣信息和平滑度實驗比較分析。分別計算測試圖像在不同類別上所產生的稀疏誤差圖的平滑度值和邊緣信息值，并將其歸一化為0～1,實驗結果如圖3所示。

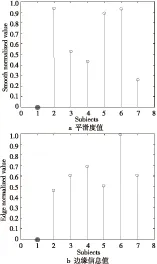
Figure 3 Extracted information from sparse error images of different face categories with scarf

圖3中，被標記點對應的是測試樣本所屬正確類別。也就是說，在同一類別上所獲得的稀疏誤差圖的平滑度值和邊緣信息值都為最小。結合這一特征，本文采用平滑度信息與邊緣信息的加權和作為判別依據，即：

(13)

由此，判別準則為：

(14)

其中，α∈(0,1)，為平滑度信息與邊緣信息之間的權衡系數。

綜合所有的因素，本文提出了基于稀疏誤差圖像的人臉識別算法，具體實現步驟如算法3所示。

算法3基于稀疏誤差圖像的人臉識別算法

輸入：訓練樣本集X=[X1,X2,…,XN]∈RM×N，測試樣本y∈RM;

輸出：測試樣本類別Subject(y)。

1.For i=1:N

根據算法1，獲取低秩表示Zi;

根據算法2，求解低秩映射矩陣Pi;

End

2.求解y在Pi上的低秩映射數據矩陣Piy，i=1,2,…,N;

4.根據式(12)，計算ei的平滑度Dsmooth和邊緣信息Dedge;

3 實驗結果及分析

本文選用Extended Yale B和AR兩個數據庫對算法進行有效性驗證。實驗主要硬件環境：Intel Pentium(R) E5500雙核處理器，主頻2.80 GHz，內存2.00 GB，WindowsXP操作系統；軟件環境：Matlab R2010a。實驗分三部分進行，首先在帶光照變化的Extended Yale B數據庫上對算法進行光照變化測試；然后再進行不同光照情況下的人為遮擋人臉識別測試；最后在具有光照變化和輕微表情變化條件下帶有持續遮擋的AR數據庫上進行真實遮擋測試。為了充分說明本文算法的有效性，將算法與傳統的LPP(Locality Preserving Projections)+NN(Nearest Neighbors)和NPE(Neighborhood Preserving Embedding)+NN，以及最近比較流行的SRC(Sparse Representation-based Classification)和LRC(Linear Regression-based Classification)四種算法進行比較。

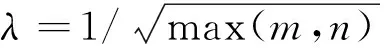
3.1 變化光照下的人臉識別

這一部分實驗在Extended Yale B數據庫上進行，該數據庫中包含38個人(即38類)，每人64幅不同光照條件下的正面人臉圖像。為了充分證實算法處理變化光照的有效性，根據文獻[13]，將每個人的所有圖像按照光照影響程度分成五個子集，從子集1到子集5光照影響程度逐步變強，每個子集分別含有7、12、12、14、19幅正面人臉圖。各子集部分圖像如圖4所示。

Figure 4 Images of the 5 subsets divided from the Extended Yale B

將子集1作為訓練樣本，其他四個子集分別作為測試樣本，進行不同光照影響下的識別測試。本文算法與NPE+NN和LPP+NN以及SRC和LRC算法進行實驗比較，表1顯示的是實驗測試結果。

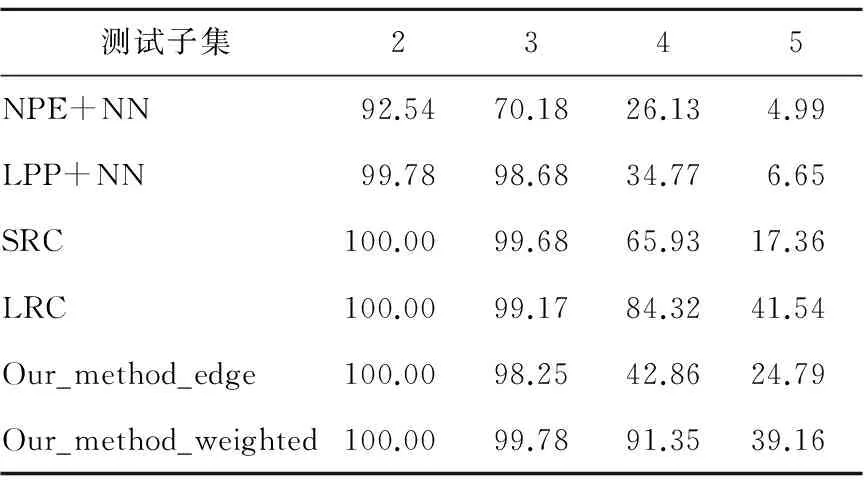
Table 1 Recognition rates of different methods with various illuminations表1 不同光照影響下的人臉識別率 %

從表1中可以獲知，在光照影響不是很大的子集2和子集3上，幾種算法的識別率都很高；隨著光照影響程度的加強，Our_method_edge算法在不同光照下所表現出的識別率明顯低于Our_method_weighted算法，證實了邊緣檢測算法對光照的敏感性，同時也證實了本文對誤差圖采用邊緣檢測與梯度求導進行加權分析的正確性；在子集4上，本文加權算法依然比較穩定，識別率為91.35%，比較多地超出其他幾種算法。不過在子集5的測試中，所有算法的識別率都嚴重下降，相對而言，SRC、LRC和本文算法的識別率表現了優勢。實驗結果證實了對誤差圖進行分析的正確性和可靠性。然而在光照影響較大的情況下，誤差圖的幾何特征變得十分模糊，所以識別率較低。

3.2 變化光照下的人為遮擋人臉識別

針對本文加權算法Our_method_weighted，為測試其在具有不同光照影響下不同物體遮擋的人臉識別情況，分別在具有不同光照程度的子集2和子集3上進行測試，并給測試人臉圖像添加不同形式的遮擋，遮擋覆蓋面積從10%到90%。實驗中分別給圖像添加隨機噪聲、狒狒臉和黑塊。圖5為測試人臉圖像分別添加30%不同形式遮擋后的效果圖。

Figure 5 Effect of adding 30% of different occlusion to a test image

將子集1作為訓練樣本，分別在具有光照變化比較明顯的子集2和子集3上進行遮擋測試。本文加權算法Our_method_weighted的測試結果如表2所示。

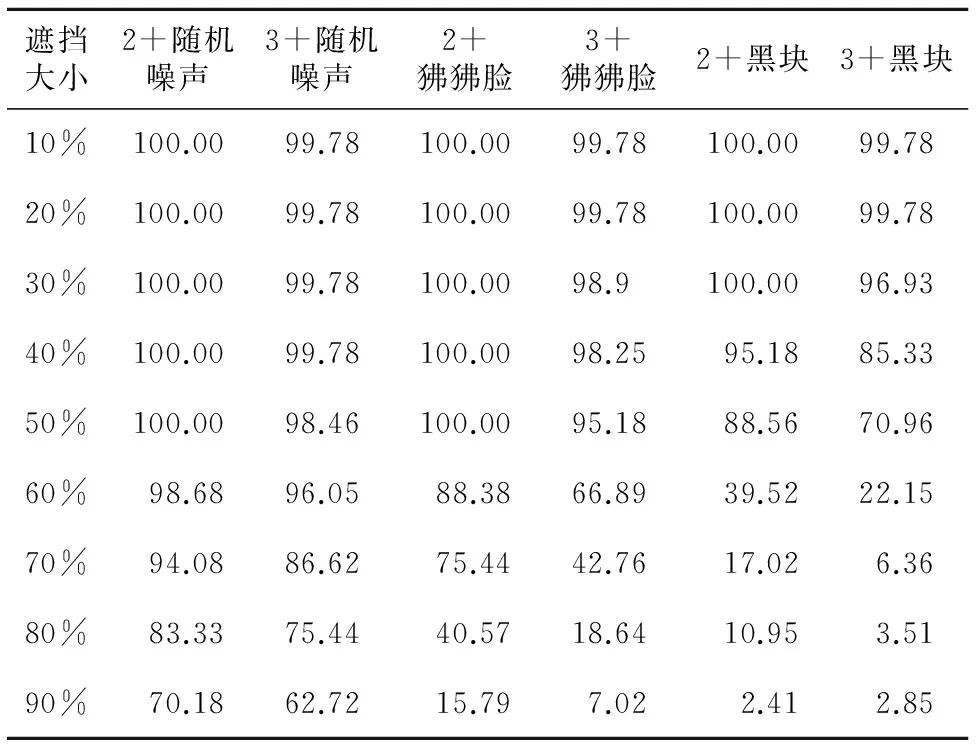
Table 2 Face recognition rates of our method weighted on different subsets with different occlusion表2 Our_method_weighted算法在不同光照影響下不同遮擋物人臉識別率 %

測試結果分析如下：(1)對隨機噪聲的遮擋，本文算法具有非常好的識別效果，表現了穩定性和極好的魯棒性，在噪聲覆蓋達60%時，子集2和子集3上的識別率都可以超過96%，并且，在覆蓋率90%的情況下，在子集2上依然保證有70.18%的識別率，而在光照影響更大的子集3上也有高達62.72%的識別率。(2)針對塊狀遮擋，也取得了比較好的識別效果。狒狒臉遮擋時，在子集2上，50%的遮擋面積下依然可以保證100%的識別率，同等情況下子集3上的識別率也可達95.18%，此外，在遮擋高達70%時，子集2上的遮擋識別率有75.44%，子集3上的識別率為42.76%，具有實際使用價值。(3)針對黑塊遮擋，在遮擋面積不高于50%時，識別效果比較穩定，然而在遮擋60%時，識別率陡降，因為黑塊不具有紋理，難于刻畫其特征，從而使得識別難度陡增。

3.3 光照變化下真實遮擋人臉識別

這一部分實驗在AR數據庫上進行。AR數據庫中包含100個人(50個男人，50個女人)，每人26張不同時間、不同表情、不同光照條件下的帶遮擋圖像。AR數據庫中的部分人臉圖像如圖6所示。

Figure 6 Some images from a subset on AR

實驗中，選用AR庫中的100個人(即100類)進行訓練與測試。每一類中，選擇八幅正常狀態下的人臉圖像作為訓練樣本集，六幅有圍巾遮擋的人臉圖像作為測試集1，六幅戴太陽鏡的人臉圖作為測試2。

Table 3 Recognition rates of different methods on AR表3 AR數據庫上各種算法的識別率 %

從表3可以比較明顯地看出，本文提出的算法取得了比其他幾種算法更好的識別效果，并且從中能夠認識到：(1)從算法本身的性質分析，NPE、LPP都是基于局部結構信息的保持，在實驗中遮擋實驗無論是墨鏡還是圍巾遮擋所表現的識別率都不理想，魯棒性不強；SRC、LRC則是從遮擋物圖像對全局數據造成的影響出發，挖掘其特征，這兩種方法在整體上對遮擋實驗的識別率有了比較顯著的提高；而本文提出的基于低秩表示的低秩映射方法則是在保持全局結構信息的基礎上最大化地尋求局部結構信息，因而能夠更加準確地識別出人臉圖像所屬類別。(2)同等條件下，SRC、LRC算法以及本文算法對墨鏡遮擋圖像識別率遠遠高于對圍巾遮擋圖像的識別率，因為圍巾遮擋部分面積明顯高于墨鏡遮擋所占面積。(3)本文算法在只對稀疏誤差圖采用邊緣檢測時，識別率明顯低于邊緣檢測信息與平滑度信息加權處理的識別率，因為邊緣檢測屬于局部上提取邊緣信息，平滑度分析則是從整個圖像的梯度角度出發，二者相結合更能反映誤差圖像的結構信息。(4)與3.2節相比，本節實驗的識別率有所降低，尤其在圍巾遮擋時表現得更為顯著。主要原因有：一為本節實驗數據中圍巾遮擋大概為40%，墨鏡遮擋大概為20%，且實驗數據除了受光照影響較大外，還包含了表情的變化，給實驗結果帶來了一定的干擾；二為本節所用的AR數據庫中類別數為100類，而3.2節所用的Extended Yale B中樣本類別數為38類，對識別率具有一定影響。

4 結束語

由于受到變化光照和局部遮擋等因子的影響，傳統的人臉識別方法受到實用性的考驗。因此，針對變化光照和局部遮擋的人臉識別問題，本文提出了基于低秩表示的稀疏誤差人臉識別算法。使用低秩表示模型將每一類訓練樣本數據都分解為低秩矩陣與稀疏矩陣和的形式并求取各類低秩映射矩陣，再利用低秩映射矩陣對測試的人臉圖像進行投影，獲取稀疏誤差圖，為了提取稀疏誤差圖中包含的全局與局部鑒別信息，分別對稀疏誤差圖進行邊緣信息計算和平滑度分析，采用兩者加權和作為人臉圖像判斷依據。在Extended Yale B和AR兩個數據庫上的實驗結果顯示了本文算法比其他算法具有更高的識別率，證實了算法的有效性和魯棒性。此外，針對光照變化明顯，遮擋面積較大的人臉識別，本文算法依舊表現出了很好的穩定性，具有較好的實際應用價值。

[1] Candès E,Li X D,Ma Y,et al. Robust principal component analysis[J]. Journal of the ACM, 2011,58(3):11,Article.

[2] Wright J,Ganesh A,Rao S,et al. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization[C]∥Proc of Neural Information Processing Systems (NIPS),2009:1.

[3] Wright J,Ma Y,Mairal J,et al. Sparse representation for computer vision and pattern recognition[C]∥Proc of IEEE,2009:1031-1044.

[4] Naseem I, Togneri R, Bennamoun M. Linear regression for face recognition [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32 (11): 2106-2112.

[5] Liu G,Lin Z,Yu Y. Robust subspace segmentation by low-rank representation[C]∥Proc of the International Conference on Machine Learning,2010.

[6] Liu G, Lin Z, Yan S, et al. Robust recovery of subspace structures by low-rank representation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(1): 171-184.

[7] Recht B，Fazel M，Parrilo P A. Guarantee minimum-rank solutions of linear matrix equations via nuclear norm minimization [J]．SIAM Review，2010，52(3): 471-501.

[8] Lin Z,Chen M,Ma Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices [J]. arXiv preprint arXiv: 1009. 5055,2010.

[9] Lin Z,Liu R,Su Z. Linearized alternating direction method with adaptive penalty for low rank representation[C]∥Proc of NIPS, 2011:1.

[10] Shi Jia-rong, Zheng Xiu-yun, Wei Zong-tian, et al. Survey on algorithms of low-rank matrix recovery[J].Application Research on Computers, 2013,30(6):1601-1605.(in Chinese)

[11] Zhuang L,Gao H,Lin Z,et al. Yu. Non-negative low rank and sparse graph for semi-supervised learning[C]∥Proc of CVPR, 2012:1.

[12] Jie Chen,Zhang Yi. Sparse representation for face recognition by discriminative low-rank matrix recovery[J]. Journal of Visual Communication and Image Representation, 2014,25(5):763-773.

[13] Luan Xiao,Fang Bin,Liu Ling-hui,et al. Extracting sparse error of robust PCA for face recognition in the presence of

varying illumination and occlusion[J].Pattern Recognition,2014,47(2):495-508.

附中文參考文獻：

[10] 史加榮,鄭秀云,魏宗田,等.低秩矩陣恢復算法綜述[J].計算機應用研究,2013,30(6):1601-1605.

楊國亮(1973-),男,江西豐城人，博士，副教授，研究方向為智能控制和圖像處理與模式識別。E-mail:ygliang30@126.com

YANG Guo-liang,born in 1973,PhD,associate professor,his research interests include intelligent control，image processing, and pattern recognition.

豐義琴(1989-),女,江西豐城人，碩士生，研究方向為圖像處理與模式識別。E-mail:feng5253995253@163.com

FENG Yi-qin,born in 1989,MS candidate,her research interests include image processing, and pattern recognition.

魯海榮(1989-),男,江西宜春人，碩士生，研究方向為圖像處理與模式識別。E-mail:1248278429@qq.com

LU Hai-rong,born in 1989,MS candidate,his research interests include image processing, and pattern recognition.

Face recognition with varying illumination and occlusion based on sparse error of low rank representation

YANG Guo-liang,FENG Yi-qin,LU Hai-rong

(School of Electrical Engineering and Automation,Jiangxi University of Science and Technology,Ganzhou 341000,China)

Although difficult to deal with, face recognition with varying illumination and occlusion has been widely investigated in recent years. Motivated by the popular methods of robust principal component analysis (RPCA) and sparse representation-based classification (SRC), we present a novel algorithm which uses the sparse error of low rank representation (LRR) for face recognition with varying illumination and occlusion. As for each type of training samples, we first calculate their low-rank matrix using LRR and then construct low rank projection between the training face matrix and the obtained low-rank data matrix. With the constructed low-rank projection, any test face image can obtain a low-rank matrix and a sparse error matrix corresponding on each face category. In order to fully extract the discrimination information of the sparse error image, its smoothness and edge information are analyzed respectively. Furthermore, a set of concrete classification criteria is proposed, which fuses smoothness information with the edge information using weighted sum rules. Experiment results on face databases of AR and the Extended Yale B confirm that the proposed method is robust to varying illumination and occlusion, and has better recognition rate than many other methods.

low rank representation;low rank projection;sparse error image;face recognition

1007-130X(2015)09-1742-08

2014-10-20;

2015-01-16基金項目：國家自然科學基金資助項目(51365017，61305019)；江西省科技廳青年科學基金資助項目(20132bab211032)

TP391.4

A

10.3969/j.issn.1007-130X.2015.09.024

通信地址：341000 江西省贛州市紅旗大道86號 江西理工大學電氣工程與自動化學院

Address:School of Electrical Engineering and Automation,Jiangxi University of Science and Technology,86 Hongqi Avenue，Ganzhou 341000,Jiangxi,P.R.China