SHPB 試驗中應力波在損傷非線彈性材料中的傳播

翟 越，李 楠，趙均海，王思維

（長安大學地質工程與測繪學院，陜西 西安，710054）

巖石類材料在沖擊載荷作用下的強度、變形與破壞規律的研究對于國防工程、隧道工程與建筑抗震等方面具有重要的現實意義，但是由于沖擊載荷施加和測量的難度大，加之非均質脆性材料的復雜性，使得這方面的研究進展緩慢．各種沖擊荷載試驗研究方法中，分離式霍普金森壓桿試驗技術(Split Hopkinson Pressure Bar, 簡稱SHPB)已成為研究中高應變率（101-104s-1）下，材料動態力學特性的最有效方法之一[1-4]．但是SHPB試驗的測量精度與數據處理方面還存在準確度較低和可靠性較差的問題，因此隨著計算機技術的迅猛發展，對于SHPB試驗的數據處理及數值模擬的研究成為熱點，并取得了一些成果[5-9]．這類問題的研究中，應力波在介質中的傳播是一個核心問題[10-11]．

本文構建了應力波在考慮損傷弱化及應變率強化效應的非線彈性巖石試件和高強度鋼制壓桿組成的桿系中傳播的波動方程，并根據試件兩端與入射桿及透射桿接觸面的應力波反射與透射關系，以及壓桿端部的自由邊界，給出初始條件和邊界條件，利用混合遺傳算法和有限差分法相結合，編制了優化數值計算程序，反演分析出試件的彈性模量、分布參數等，進而得到試件的應力、應變數值．通過計算應力-應變曲線和試驗曲線對比，驗證了非線彈性應力波動方程的可靠性，以及數值分析方法的適用性．

1 應力波在細長桿件中的波動方程

1.1 應力波在長細桿件中的傳播理論

將SHPB試驗的數值分析問題，轉化為在物質坐標中研究應力波在一組不同材料等直截面的細長桿系中的縱向傳播問題．取變形前(時間 0t= )質點的空間位置作為物質坐標，桿系中心軸線為X軸，如圖1所示．設定桿在變形前的初始截面積0A(m2)、初始密度0ρ(kg/m3)和其它材料性能參數都與坐標無關，截面形狀一般也無限制．

應力波在各種介質內傳播的問題中，波動方程是最基本、最重要的理論基礎．波動方程的建立可以通過聯立運動方程、動力方程和介質材料的物理方程，即本構方程[12]，組成的方程組求解三個未知函數應力),(tXσ，應變),(tXε和質子速度),(tXv，從而得到應力波在該材料中傳播的波動方程．下面分別探討應力波在線彈性鋼制壓桿以及考慮損傷的非線彈性巖石試件中傳播的波動方程．規定應力和應變均以拉為正，而質點速度以沿X軸正方向為正，反之為負．

圖1 質點空間位置的物質坐標Fig.1 Space coordinates of material point

1.2 應力波在線彈性細長桿件中的波動方程

運動學方程，即連續方程或質量守恒方程，由位移u的單值連續條件就可得到聯系應變ε和u的相容性方程，如式(1)所示．

動力學方程，即動量守恒方程，利用連續性條件可以得到：

材料本構方程，即物理方程，可以表示為應力與應變的連續函數．SHPB裝置的撞擊桿、入射桿和透射桿都是由高強度不銹鋼制成，其材料在一般加載條件下可以看成理想線彈性體，因此其符合胡克定律，即：

式中，0E為材料的初始彈性模量，單位MPa．聯立求解式(1)、式(2)和本構方程(3)，則應力波在線彈性材料中的波動方程可表示為：

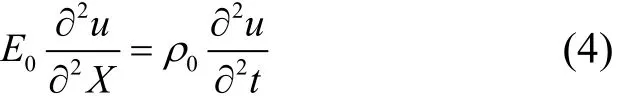
1.3 應力波在考慮損傷的動態非線彈性桿件中傳播的波動方程

1.3.1 考慮損傷的動態非線彈性本構模型

當加載應變率較大時（100s-1以上），巖石類材料的應力-應變曲線呈現出明顯的非線性，此時用線彈性本構模型來描述顯然不太適合．國內外學者提出多種的非線性本構方程，其中，Saenz[13]建立的非線性本構模型，在鋼筋混凝土的有限元分析中有廣泛的應用[14]，其公式如下所示：

式中：B、C分別為材料的特征參數；fε為峰值應力對應的應變．

為了考慮損傷對巖石類材料力學性能的影響，根據應變等效原理，受損材料的本構方程可由損傷后的有效應力來取代無損材料本構方程中的名義應力，從而構建出[15]，因此本文引入考慮閾值的統計損傷演化因子w，如下式．

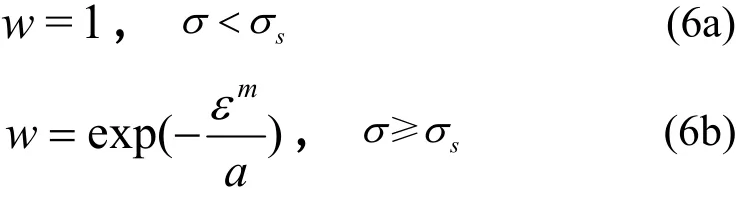
式中，m和a為損傷因子的分布參數；sσ為損傷應力閾值，單位Pa．當應力小于它時，不考慮損傷．

同時，為了考慮沖擊荷載作用下的應變率相關性，引入應變率強化因子dR，如式(7)所示：

式中，λ是材料參數，反映巖石類材料受壓時的率效應；ε˙表示在動荷載作用下反映材料動態響應的應變率，單位為s-1，在SHPB試驗中一般取平均應變率值．

將式(6)和式(7)分別代入式(5)，則構建出考慮損傷的動態本構方程，如式(8)所示：

式中，參數意義同前所述，其中sσ、fε和˙ε分別可由試驗得到，其他特征參數可以在試驗研究基礎上，通過優化反演分析確定出來．

1.3.2 應力波在非線性粘彈性材料中的波動方程

建立應力波在非線彈性材料中的波動方程時，采用上述式(8)作為巖石類材料的本構方程，將其與運動學方程(1)和動力學方程(2)聯立求解，可得考慮損傷的非線彈性應力波波動方程微分形式，如式(9)所示：

2 巖石類材料動態特性的數值分析

2.1 數值計算基本假定

為了便于數值計算，在可靠性可以接受的情況下，作如下假定：首先，桿件在變形時橫截面始終保持為平面，沿橫截面只有均布的軸向應力，因此各材料參數都只是位置X和時間t的函數，整個問題簡化為一維問題，而忽略桿中質點橫向運動的慣性作用，即不計橫向收縮或膨脹對動能的影響．根據桿中彈性波的精確解可知，只要波長比桿的橫向尺寸大很多時，這一近似假定所引起的誤差是允許忽略的[2]；其次，由于應力波波速很高，在通過微元體的瞬間，微元體還來不及和鄰近的其它微元體進行熱量交換，因此可近似地認為沖擊加載過程是絕熱的，無需列出能量守恒方程，就可得到關于變量σ、ε和v的封閉的控制方程組．數值分析及試驗所用的SHPB裝置示意圖如圖2所示．

圖2 SHPB結構圖Fig.2 Sketch map of SHPB apparatus

2.2 壓桿和試件中應力波波動方程的有限差分解

有限差分是一種常用的數值解法，它是用差商代替偏導數，得到在微分方程的差分形式，通過解差分方程得到微分方程解的近似值．應力波在鋼制壓桿中的波動方程式(4)，可用有限差分法的中心差分格式表述如下：

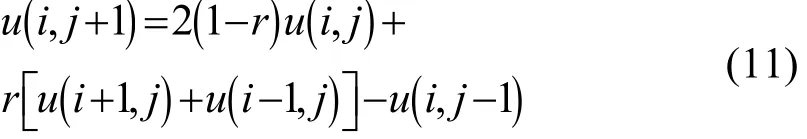
試件中的應力波波動方程式（9）的有限差分解可按上述中心差分方法得到．

2.3 初始條件和邊界條件

2.3.1 初始條件

假設在加載過程中，子彈和入射桿始終保持接觸狀態，此時在接觸面上的軸向方向，兩桿的質點位移相同，即初始條件為：時間點為1時（j=1），入射桿初始端與子彈接觸面上質點的位移 Wz(i,1)等于接觸面上子彈質點速度 Vi( 1)與時間的乘積：

由此，將試驗測得的子彈撞擊波形整形器改進后的入射桿時產生的半正弦加載應力波（如圖3）通過初始條件直接加載在入射桿的初始端．

2.3.2 邊界條件

要數值模擬應力波在整個SHPB壓桿和試件中的傳播，必然要確定壓桿兩端的邊界條件，以及試件和壓桿的接觸面上的邊界條件．這里將試件在動態沖擊荷載作用下的慣性和端頭摩擦效應忽略不計．

(1) 桿件端部邊界條件

當端部固定時，由于入射波 R (C0,t)與反射波F(C0,t)的疊加，其邊界條件為端頭處的位移 u0始終為零，而應力σ0為入射時的2倍．其中C0為應力波波速．

當端部自由時，同樣由于入射波 R (C0,t)與反射波F(C0,t)的疊加，邊界條件為自由端的應力為零，而位移為入射時為2倍．

(2) 兩種介質接觸面上的邊界條件

由于壓桿和巖石試件的阻抗(00Cρ)存在較大差異，根據一維應力波在不同介質的傳播理論[11]，SHPB試驗中的應力波會在兩種介質的接觸面上發生反射與透射．試驗中測得的入射波和反射波是在入射桿上測得的，而透射波是在透射桿上測得的，也就是第一個界面的透射波通過試件傳播到第二個界面產生的透射波，因此試驗測量的三個波并不是在同一界面上發生的．在相同壓桿和入射波R(C0,t)的條件下，反射波 F (C0,t)和透射波 T (C0,t)的大小是由試件的阻抗所決定的，計算公式如下所示：

式中，F和T分別為應力波由壓桿向巖石類材料傳播時的反射系數和透射系數，可由下式計算：

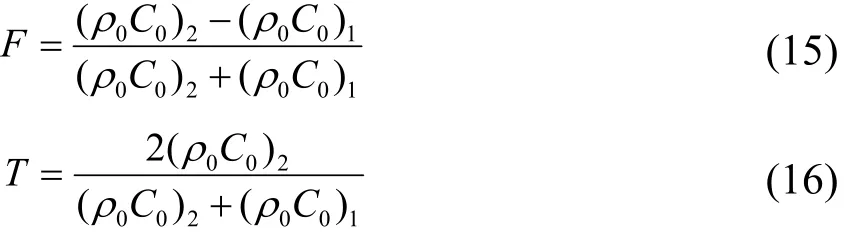
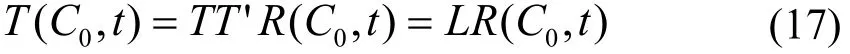
式中，T′為應力波由巖石試件向透射桿透射的系數；L為應力波由入射壓桿向試件透射后，再由試件向透射桿透射的兩次透射系數，可表示為：

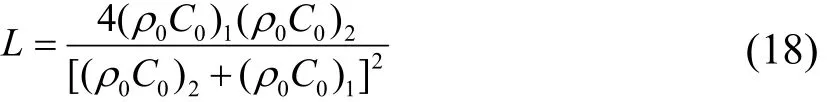
2.4 數值分析程序及計算結果分析

2.4.1 花崗巖SHPB試驗及數值分析程序

為了給數值分析提供試驗基礎，對花崗巖試件進行了SHPB試驗，所用裝置如圖2所示．SHPB系統的壓桿和子彈的材料均為高強度不銹鋼，直徑皆為50 mm，入射桿、透射桿和吸收桿的長度皆為2 000 mm，子彈長度為300 mm，并采用了直徑為18 mm、厚度為1 mm的圓形銅片作為波形整形器，將應力波改進為半正弦波[16]，如圖3所示．試驗中控制氣壓為0.8 MPa，子彈沖擊速度為12.84 m/s，測得平均應變率為50 s-1．

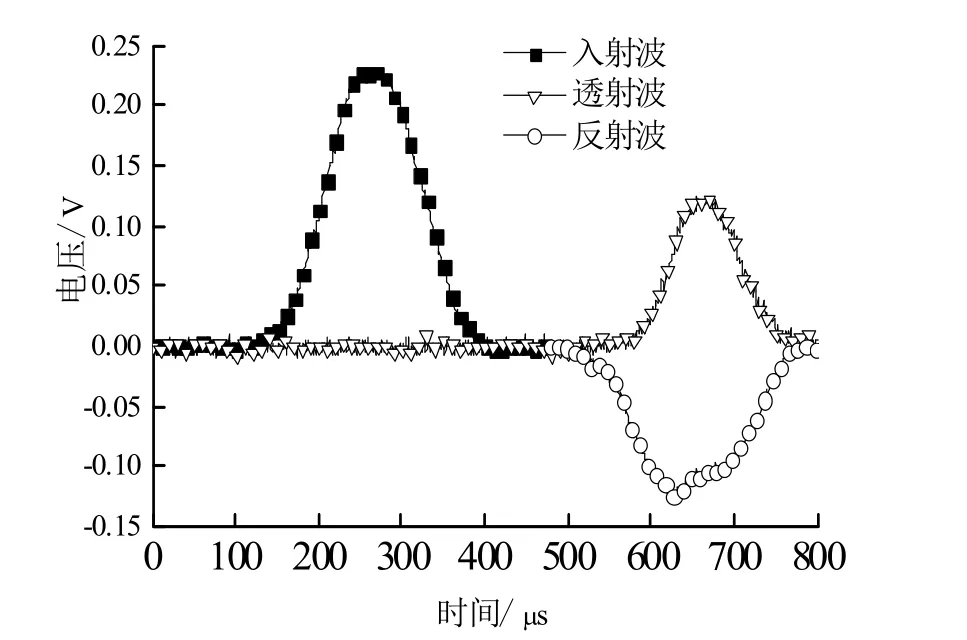
圖3 加脈沖整形器后的波形圖Fig.3 Pulse curve with pulse shaper

基于上述有限差分法求解波動方程、初始條件和邊界條件所組成的方程組，應用VC++編寫了巖石類材料的動態分析程序．在數值計算時，應得到非線性本構方程中的特征參數．為此編制了自適應混合遺傳算法[17]，并嵌入到有限差分程序中，實現每一次數值分析應力波傳播的同時進行優化反演分析，從而確定波動方程中的待定參數．數值分析中的物理參數選取如表1所示．

表1 數值模擬程序的計算參數選取Tab.1 Count parameter of numerical simulation program

2.4.2 數值分析結果

基于試驗數據，通過有限差分數值計算和優化反演的混合程序，確定出花崗巖的動態本構模型的特征參數如表2所示．

表2 花崗巖非線彈性動態本構模型反演分析結果Tab.2 Inversion Analysis results of nonlinear elastic constitutive model

為了和試驗結果比較，取數值分析中壓桿中心處的應力應變值，作為花崗巖試件的平均應力和應變．試驗應力-應變曲線和計算應力應曲線的對比如圖4所示．圖中，兩曲線有較好的一致性，表明所采用考慮損傷弱化和應變率強化的非線彈性本構方程和在此基礎上推導出來的非線彈性應力波波動方程都是適用和可靠的，同時也驗證了這種數值分析方法是合理的．

圖4 花崗巖的試驗曲線和再生曲線（應變率50s-1）Fig.4 Test curve and reproduction curve of granite

這種方法相對于SHPB傳統數據處理方法的兩個最突出的優點，一是采用的數據可以采自壓桿的任意位置；二是不再要求入射桿和透射桿要滿足足夠的長度．該方法適用于各種巖石類材料和低阻抗材料的動態特性的研究，為SHPB裝置的試驗結果分析與數據處理提出一種有效的方法．

3 結 論

(1) 基于考慮損傷弱化和應變率強化的非線彈性動態本構方程，及相應的運動方程和動力方程，建立了應力波在巖石類材料桿件中傳播的波動方程；

(2) 在上述波動方程的基礎上，利用有限差分法編制了可以分析了沖擊加載波由入射桿傳播到試件再到透射桿的整個加載過程的數值計算程序；

(3) 將數值程序與混合遺傳算法相結合，辨識出方程的特征參數，將理論計算結果與試驗結果比較得到了可靠性驗證．

References

[1] DAI feng, HUANG Sheng, XIA Kaiwen, et al Some fundamental issues in dynamic compression and tension tests of rock using split Hopkinson pressure bar[J]. Rock Mech Rock Eng, 2010, 43: 657-666.

[2] EZIO Cadoni. Dynamic characterization of orthogenesis rock subjected to intermediate and high strain rates in tension[J]. Rock Mech Eng, 2010, 43: 667-676.

[3] YAN fei, FENG Xiating, CHEN Rong, et al. Dynamic tensile failure of the rock interface between tuff and basalt[J]. Rock Mech Rock Eng, 2012, 45: 341-348.

[4] 翟毅, 許金余, 王鵬輝. 纖維混凝土動態壓縮力學性能的SHPB試驗研究[J]. 西安建筑科技大學學報: 自然科學版, 2009, 41(1): 141-148.ZHAI Yi, XU Jinyu, WANG Penghui. Dynamic compressive testing and mechanical behavior of fiber reinforced concrete using a split Hopkinson Pressure Bar[J]. J. Xi’an Univ. of Arch. &Tech: Natural Science Edition, 2009, 41(1): 141-148.

[5] 江見鯨, 賀小崗. 工程結構計算機仿真分析[M]. 北京:清華大學出版社, 1996.JANG Jianjing, HE Xiaogang. Computer simulation analysis of engineering structure[M]. Bejing: Tsinghua University press, 1996.

[6] 唐志平, 王禮立. SHPB試驗的電腦化數據處理系統[J].爆炸與沖擊, 1986, 6(4): 320-327.TANG Zhiping, WANG Lili. Computerized data processing system of SHPB experiment[J]. Explosion and Shock Waves, 1986, 6(4): 320-327.

[7] LIFSHITZ J M, LEBER H. Data processing in the split Hopkinson pressure bar tests[J]. International Journal of Impact Engineering, 1994, 15(6): 723-733.

[8] LI X B, LO T S, Zhao J, et al. Oscillation Elimination in the Hopkinson bar apparatus and resultant complete dynamic stress-strain curve for rocks[J]. International Journal of Rock Mechanics & Mining Sciences, 2000, 37:1055-1060.

[9] HAO Y, HAO H. Numerical investigation of the dynamic compressive behaviour of rock materials at high strain rate[J]. Rock Mech Rock Eng, 2013, 46: 373 -388.

[10] FOLLANSBEE P S, FRANTZ C. Wave propagation in the split Hopkinson pressure bar[J]. Journal of Engineering Materials Technology, 1983, 105: 61-66.

[11] FAN L F, REN F, MA G W. Experimental study on viscoelastic behavior of sedimentary[J]. Rock Mech Rock Eng, 2012, 45: 433-438.

[12] 王禮立. 應力波基礎[M]. 北京: 國防工業出版社, 2005.WANG Lili. Foundations of Stress Waves[M]. Beijing:National Defense Press, 2005.

[13] SAENZ L P. Discussion of Equation for the Stress-strain Curve of Concrete by Desay and Krishnan[J]. Journal of ACI, 1964, 61(9): 1229-1235.

[14] 呂西林, 金國芳, 吳曉涵. 鋼筋混凝土結構非線性有限元理論與應用[M]. 上海: 同濟大學出版社, 1996.Lü Xilin, JIN Guofang, WU Xiaohan. The structure of the nonlinear finite element theory and application of reinforced concrete[M]. Shanghai: Tongji University press, 1996.

[15] 商懷帥, 楊魯生. 基于損傷理論的混凝土雙軸壓本構模型[J]. 中南大學學報: 自然科學版, 2013, 44(1): 340-344.SHANG Huaishuai, YANG Lusheng. Constitutive model of damage of concrete under biaxial compression[J].Journal of Central South University: Science and Technology, 2013, 44(1): 340-344.

[16] 翟越, 馬國偉, 趙均海, 等. 花崗巖和混凝土在沖擊荷載下的動態性能比較研究[J]. 巖石力學與工程學報,2007, 26(4): 762-768.ZHAI Yue, MA Guowei, ZHAO Junhai, et al. Dynamic capability of granite and concrete under impact compressive loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(4): 762-768.

[17] 翟越, 趙均海. 基于自適應混合遺傳算法的巖石類材料動態參數反演分析[J]. 地球科學與環境學報, 2008,30(3): 286-291.ZHAI Yue, ZHAO Junhai. Inverse analysis based on adaptive hybrid genetic algorithms for dynamic characteristic parameters of rock materials[J]. Journal of Earth Sciences and Environment, 2008, 30(3): 286-291.