巴特沃斯濾波器在高保真音響系統中的應用
陶有軍
(西安理工大學 高等技術學院,陜西 西安 710082)
人們的生活離不開音樂,音響系統則是重放音樂信號最常用的設備,因為大功率全頻帶的揚聲器很昂貴,所以音頻信號都要通過分頻器分為高低不同的成分,分別送到不同頻帶的揚聲器去還原。分頻器有后級功率分頻和前級電子分頻之區別。功率分頻因為成本低,效果好而被人們廣泛接受。電子分頻雖然成本高,但因其音質更佳也有一定的市場。目前,解決前級電子2分頻、3分頻電路的幅頻特性、相頻特性的問題,發燒友們在打造音響系統時各有其道,但真正經過細化研究、可以照章索取的資料好像很是有限。
1 巴特沃斯高、低音2階2分頻器
前級電子分頻電路不僅要把音樂信號從幅度上分為高、低兩個頻段,而且要保證從高通和低通濾波器中通過的同頻率信號,它們的相位必須保持一致,否則就產生了相位失真,在高保真音響技術中,這是不允許的。
筆者經過理論仿真與實物制作發現,嚴格按巴特沃斯濾波器參數設計的2分頻2階濾波器,只要將其中一路的信號倒相,就能夠嚴格滿足上述要求,而且巴特沃斯2階濾波器的幅頻特性非常平坦,性能自然優異。但美中不足是它的衰減特性是40 dB/sec,重疊部分比較寬。圖1所示電路A點之前為高低頻提升電路,B點之后是按巴特沃斯濾波器參數設計的1 kHz為分頻點的2分頻2階濾波器。由于分頻點附近兩個通道里都有1 kHz左右的信號,且衰減緩慢,造成疊加后中音頻率帶明顯提升。以仿真實驗為例,在圖1的電路中,去掉高低頻提升電路,也就是將電路中A、B兩點之間斷開,將信號源直接加在分頻器輸入端B點,取80 Hz,800 Hz,10 000 Hz 3個典型頻率作為輸入進行測試,圖2所示為80 Hz、10 000 Hz信號輸出振幅均為1.75 V時,分頻點附近800 Hz信號在兩個通道里的輸出波形,顯然其振幅大約為2.5 V(1.5 V+1 V)。因為人的聽覺對于中音的失真最為敏感,所以中音帶相對提升對改善音質不利。
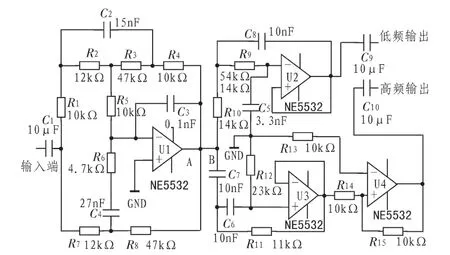
圖1 1 kHz為分頻點的2階濾波器Fig.1 1 kHz frequency division 2 order filter
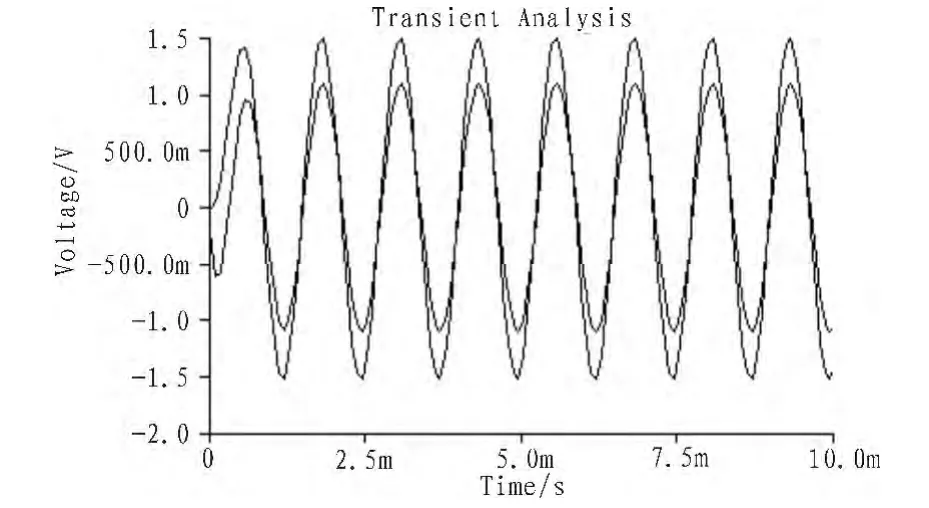
圖2 800 Hz信號通過2分頻器后的波形Fig.2 800 Hz signal after the frequency divider by 2 waveform
以上波形雖然為仿真結果,經實物電路驗證結果基本一致。為彌補中音頻率帶明顯提升這一缺陷,如圖1所示可以在分頻器之前加一個高低音補償電路,電路的元器件參數要反復設計與仿真,力求整體系統的幅頻特性平坦。仿真結果如圖3所示,當80 Hz,10 000 Hz信號輸出振幅均為1.75 V時,分頻點附近800 Hz信號在兩個通道里輸出波形的振幅相加也大約為1.75 V(1.0 V+0.7 V)左右。在全音頻范圍內測試其幅頻特性,發現在高、中、低3個區域內幾近平坦。經過實物試聽,總體音質非常好,高音纖細透亮,中音明亮柔和,低音渾厚飽滿。當然這也需要高性能的后級功放作支撐。
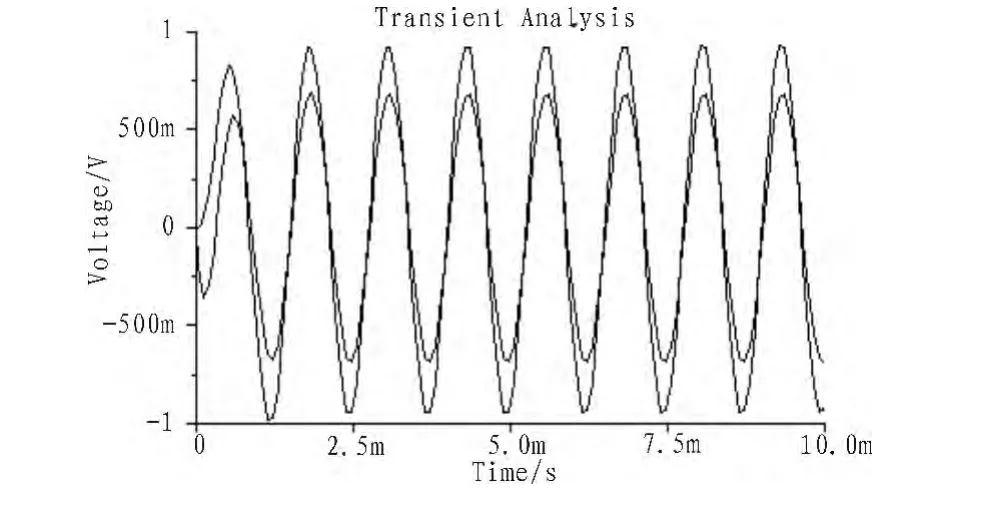
圖3 800 Hz信號通過2分頻器后的波形Fig.3 800 Hz signal after the frequency divider by 2 waveform
2 巴特沃斯高、中、低2階3分頻器
高保真前級電子分頻器的難點在于,完成幅度分頻的同時,要保證分頻點附近不同的通道中同一信號的相位必須一致。在兩分頻電路中這一點不難做到,但是在三分頻電路中就不一樣了,必須附加相位校正電路。假如選定兩個分頻點分別是800 Hz和4 000 Hz,第一種設計思路是分別設計800 Hz的低通濾波器、4 000 Hz的高通濾波器及800~4 000 Hz的帶通濾波器,這樣設計的結果是分頻點附近高、中、低3個通道中同一信號的相位相互不同,除非以其中一個通道為基準,其它兩個通道加上合適的相位校正電路,這樣做難度很大。圖4就是基于上述思路設計的電路,圖5則是分頻點附近3個通道里輸出1 200 Hz時的仿真波形,顯然它們的相位互不相同,補償困難。
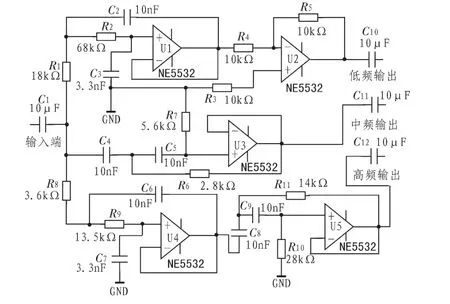
圖4 第一種三分頻電路Fig.4 The first three points frequency circuit
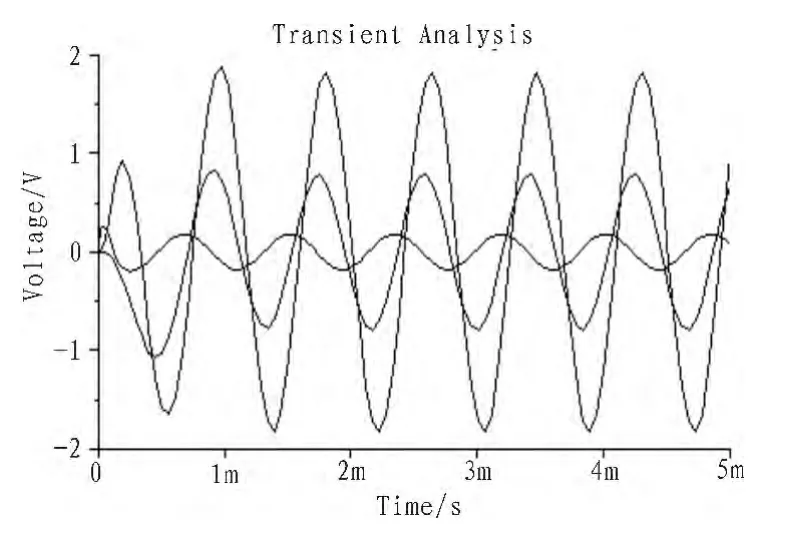
圖5 1 200 Hz通過3個通道后的波形Fig.5 Waveform after 1 200 Hz through three channels
第二種設計思路是先將整個頻段以800 Hz為準分為高、低兩個頻段,再將高頻段以4 000 Hz為分頻點分為中、高兩個頻段,如此一來,后兩個通道在頻率重疊區的信號不會發生相位失真,只要在低通濾波器后面加上一個合適的相位校正電路,其頻率重疊區信號相位失真情況就會得到明顯改善。圖6所示為基于第二種思路設計的濾波器電路,元件R17、C12、R19、C14是針對低音通道附加的相位校正電路。圖 7 所示為去掉相位校正電路時,1 200 Hz信號經過三個通道后的仿真波形,顯然其中兩個波形的相位是一致的,只要想辦法補償低頻通道的信號就可以了。
加上相位校正電路后,重新測試發現,在3個通道的頻率重疊區域基本消除相位失真。圖8所示為1 200 Hz信號分別經過高、中、低三通道后的仿真波形。在重疊區的其它頻率點上測試,效果基本相同。
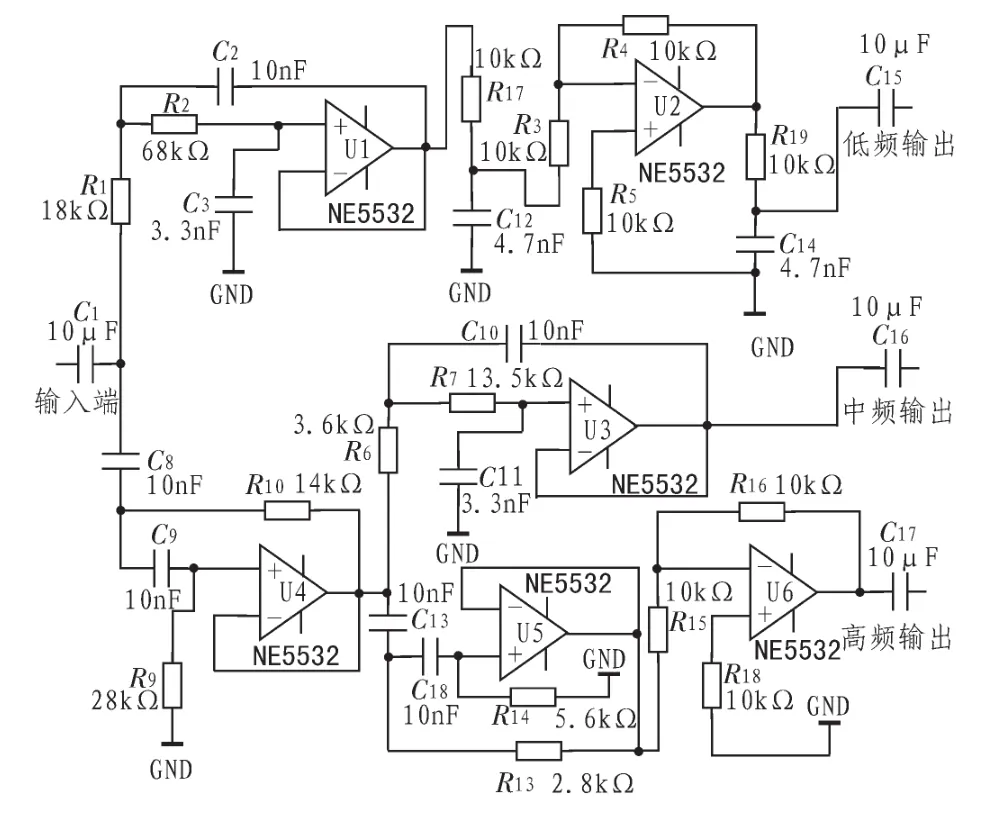
圖6 第二種三分頻電路Fig.6 The second three points frequency circuit
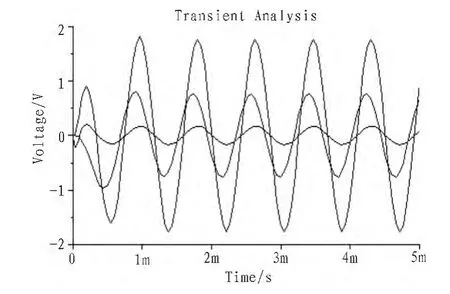
圖7 1 200 Hz信號通過三個通道后的波形Fig.7 Waveform after 1 200 Hz through three channels
3 結束語

圖8 1 200 Hz信號通過3個通道后的波形Fig.8 Waveform after 1 200 Hz through three channels
高保真音響系統中的分頻器,在進行幅度分頻的同時要保證相位不會產生失真,巴特沃斯濾波器就是首選的電路之一,但是為提高音質,針對不同的分頻器還需要做一些改進。比如改善信號幅頻特性的高低音提升電路,改變相頻特性的相位校正電路等。通過這些措施,力求音頻信號從信號源到揚聲器之間的通道中既不產生幅度失真也不產生相位失真,這樣的音響系統才真正接近高保真。
[1]Ray Alden.揚聲器系統設計與制作進階[M].北京:人民郵電出版社,2013.
[2]Douglas Self.音頻功率放大器設計手冊[M].北京:人民郵電出版社,2009.
[3]劉南平.電子產品設計與制作技術[M].北京:科學出版社,2009.
[4]李新平.實用電子技術與仿真[M].北京:機械工業出版社,2003.
[5]王興亮,洪琪,達新宇,等.現代音響與調音技術[M].西安:西安電子科技大學出版社,2002.
[6]《電子報》編輯部.電子報合訂本[M].成都:電子科技大學出版社,2001.
[7]D.E約翰遜,J.L希爾伯恩.有源濾波器的快速實用設計[M].北京:人民郵電出版社,1986.

