改進自適應中值濾波算法研究

華顯立，倪江楠

（河南工業職業技術學院 河南 南陽 473009）

在數字圖像信號的形成、傳輸和接收過程中，因各種因素的影響，實際數字圖像中的信號總是和噪聲共存。由于噪聲嚴重地影響了圖像的質量和視覺效果，因此在進行圖像分割、邊緣檢測、特征提取等處理之前，對圖像噪聲進行濾波是必不可少的。中值濾波是處理椒鹽噪聲的一種常用方法，既能有效抑制椒鹽噪聲，又能保護圖像的細節、邊緣，對低密度分布的椒鹽噪聲具有良好的去除效果，故在圖像處理領域得到了廣泛應用。大量研究表明：中值濾波的去噪性能受濾波窗口的形狀和大小的影響較大，在抑制圖像噪聲和保護細節兩方面存在一定的矛盾[1]：濾波窗口越小，可較好保護圖像細節，但去噪能力會受到限制；反之，濾波窗口越大，就可加強噪聲抑制能力，但對細節的保護能力會減弱。尤其在去除細節較豐富的圖像噪聲時，往往會將非噪聲點誤判斷為噪聲點，造成圖像中相對濾波窗口較“細小”的諸如點、細線、拐角和紋理等細節結構的丟失或破壞，而這些“細小”結構往往包含圖像中的重要信息。選擇合理的濾波窗口尺寸，是使中值濾波達到最佳濾波效果的關鍵。標準中值濾波的濾波窗口大小是預先設定的，無法自主選擇最佳窗口尺寸，去噪性能不穩定。為此提出了自適應中值濾波方法[2]。

1 自適應中值濾波（AMF）

自適應中值濾波，其基本思想是基于由m×n矩形濾波窗口Sxy定義的區域內圖像的統計特性，對比預先設定的約束條件判斷是否需要擴大窗口S的大小。即能夠根據預設條件自主選擇最佳窗口尺寸，在最終選定的濾波窗口內進行中值濾波。

設圖像大小為 M×N，f(i，j)為圖像信號點(i，j)對應的灰度值，W(i，j)為以(i，j)為中心的矩形濾波窗口，初始窗口常取為 3×3，預設的最大窗口為 Wmax；fmax、fmin、fmed分別為 W(i，j)中的灰度最大值、最小值和中值。自適應中值濾波算法有兩個層次，分別定義為A層和B層:

A 層:設定初始窗口大小，若 fmin＜fmed＜fmax，則轉至 B 層；否則增大窗口 W(i，j)的尺寸，若 W(i，j)的尺寸小于 Wmax的尺寸，則重復第 A 層，否則 原值輸出 f(i，j)。

B 層:對圖像各區域進行噪聲點檢測，若 fmin＜f(i，j)＜fmax，輸出原始灰度值 f(i，j)，否則輸出濾波窗口中值 fmed。

由于對噪聲點和信號點采用不同處理方法，更好地保護圖像細節，有效緩和了抑制噪聲和保護細節兩者之間的矛盾[2]；亦減少了計算量，提高了運算效率。但是，簡單的認為區域內的極值點就是噪聲點，可能導致將邊緣信號點誤判為極值點，從而誤判為噪聲點進行中值濾波，導致圖像邊緣或細節的損失；當達到濾波窗口最大尺寸，窗口中值仍為極致點時，直接輸出中心像素點灰度值，將導致部分噪聲點不能被濾除（即漏判），濾波質量下降。

2 改進型自適應中值濾波算法

自適應中值濾波在噪聲密度較小時，濾波效果和細節保持能力均較好；當噪聲密度大于50%時，為了更好地去噪必須增大濾波窗口，從而導致邊緣、細節等被破壞。同時，對于細節豐富的圖像，必須盡可能地使用小窗口進行濾波，為了緩和了抑制噪聲和保護細節兩者間的矛盾，提出了改進的自適應中值濾波算法[3－6]。

2.1 改進算法1（IAMF1）

這種改進算法是基于小窗口非空信號點的：首先檢測最小窗口，當窗口中所有像素都被噪聲污染時，即非噪聲污染像素點（稱為信號點）的數目為零時，才會擴大窗口[5]。否則，就采用此窗口中未被噪聲污染像素的灰度進行中值濾波，即只要當前濾波窗口內存在信號點就不擴大窗口，就可以維持較小窗口的中值輸出，從而較好地保持了圖像細節。所謂非噪聲污染像素（信號點），是指當前濾波窗口內灰度值滿足像素點集合，流程圖如圖1所示。

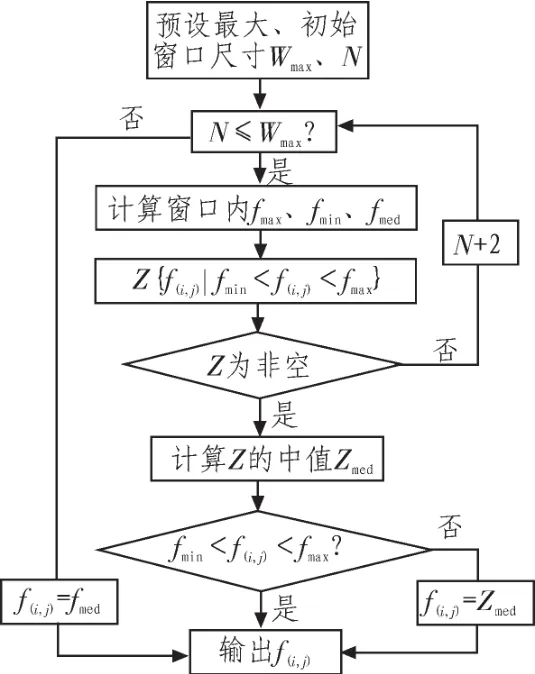
圖1 改進算法1流程圖Fig.1 Flow chart of IAMF1

2.2 改進算法2（IAMF2）

隨著噪聲密度的增大，首次包含非空信號點的窗口尺寸亦增大，同時將邊緣、細節等信號點誤判為噪聲點的幾率亦增加。自然圖像相鄰像素點間存在著很大的相關性，像素點間的距離越近相關性越大。引入最小幾何距離測度[6](簡稱MSD)。MSD定義為:

f(i，j)為(i，j)中心像素點的灰度值，Z 為當前濾波窗口內未污染點的集合。MSD反映了中心像素值與未污染集合的相關性，MSD越小相關性越大，表明f(i，j)是未污染點（信號點）的可能性越高。 根據統計特性設置閥值 k，當 MSD＜k時，可認為 f(i，j)為信號點，否則為噪聲點。

具體流程如圖2，主要步驟為：1)設定最大、初始濾波窗口N=Wmax、N=3，閾值k，未污染點集合Z初始為空。2)計算當前濾波窗口內的灰度最大 fmax、最小值 fmin。 3)若 f(i，j)滿足 fmin＜f(i，j)＜fmax，判定為信號點，直接輸出 f(i，j)，否則計算未污染點集合 Z。若 Z 為空集，且 N＜Wmax，擴大窗口，令 N=N+2，轉步驟 2)；若 Z為非空，計算Z的中值Zmed，并計算N=Wmax時的Z值Z′。4)若N=Wmax，判斷 Z 是否為空。若為空，則輸出 f(i，j)；否則計算 MSD。5)若 MSD＜k，判定為信號點，濾波輸出 f(i，j)；否則判定為噪聲點，濾波輸出Z的中值Zmed。

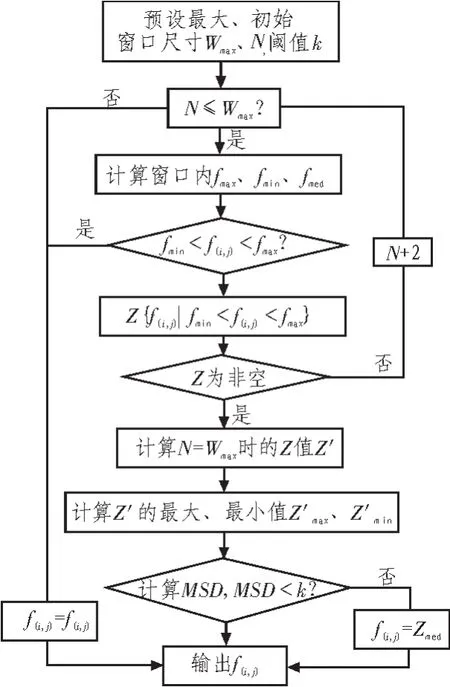
圖2 改進算法2流程圖Fig.2 Flow chart of IAMF2

需要強調的是：由于濾波窗口大，平滑作用強；濾波窗口小，能更好的保持圖像邊緣、細節。因此，步驟4)在計算MSD=選擇的Z，其范圍為最大濾波窗口N=Wmax時的Z′，在最大非空集合內能夠更準確判斷中心象素是否為信號點。像素點間距離越近，相關性越大，步驟5)的噪聲點輸出時，其非空集合選擇的是Z，能更好保持圖像細節。

3 去噪效果比較及分析

在MATLAB7.1上，采用lena標準測試圖像進行仿真實驗。分別對測試圖像加20%、30%、50%、70%、80%、90%強度的椒鹽噪聲，再用自適應中值濾波算法、改進算法1、改進算法2對加噪圖像做濾波處理，最大濾波窗口設為9、MSD的閾值k設置為2。實驗結果如圖3、4。可看出自適應中值濾波算法的去噪能力隨椒鹽噪聲概率密度增加越來越弱，在椒鹽噪聲大于30%后，出現明顯椒鹽點，漏檢率增加，改進算法1、改進算法2的去噪效果較好。從圖4看出，即使是超高密度噪聲，去噪后的圖像中幾乎不存在噪聲點，細節保持也較好。

采用峰值信噪比PSNR作為客觀評價標準比較3種算法，如表1所示，PSNR保持在25 dB以上；尤其是在高密度噪聲時，改進算法的PSNR比改進前的提高17 dB以上，顯示數據與視覺評價結論一致。兩種改進算法在不同噪聲密度下的PSNR相差不大，主要是由于隨著噪聲密度的增加，首次包含非空信號點的窗口尺寸N更接近于最大濾波窗口，就與亦很接近，即兩種改進算法的用來判斷是信號點或噪聲點的標準幾乎相同，濾波效果基本一樣。但改進算法2的運算時間稍長于改進算法1。

圖3 3種算法的濾波結果Fig.3 Filtering results of three filters

圖4 3種算法的濾波結果Fig.4 Filtering results of three filters

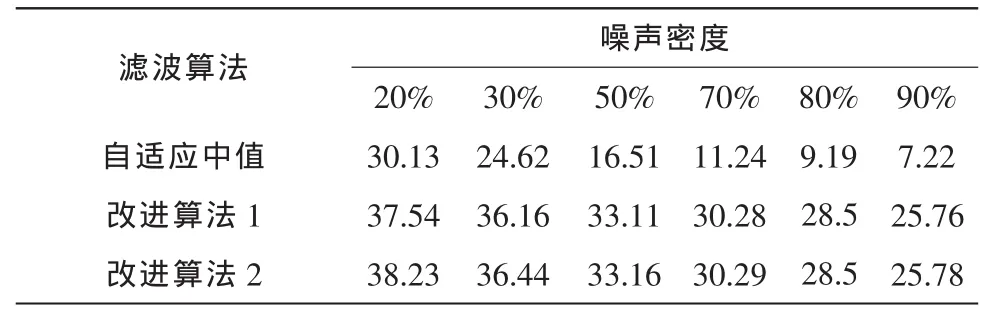
表1 3種濾波算法在不同噪聲密度下的PSNRTab.1 Results in PSNR at various noise density for three filters

4 結論

本文運用自適應中值濾波算法及兩種改進算法對不同噪聲密度的圖像去噪。仿真實驗結果表明：圖像主觀視覺評價和PSNR客觀評價結果一致，兩種改進算法去噪效果基本相同，都優于自適應中值濾波算法；改進算法的PSNR保持在25 dB以上，在高密度噪聲時也能得到細節較為清晰的圖像，PSNR比改進前的值提高17 dB以上，但運算時間較長。實際圖像濾波時，可結合噪聲強度估計的思想，對未知噪聲強度的圖像，先進行噪聲強度估計，若椒鹽噪聲為0.3以下進行自適應中值濾波算法，0.3以上運用改進算法1或改進算法2進行濾波。

[1]Ataman E,Aatre V K,Wong K M.Some statistical properties of median filters[J].IEEE Trans on Acoustics,Speech and Signal Processing,1981,29(5):1073-1075.

[2]Hwang H,Haddad R.Adaptive median filters:new algorithm and results[J].IEEE Transactions on Image Processing,1995(4):499-502.

[3]邢藏菊,王守覺,鄧浩江，等.一種基于極值中值的新型濾波算法[J].中國圖象圖形學報，2001,6(6):533-536.XING Zang-ju,WANG Shou-jue,DENG Hao-jiang,et al.A new filtering algorithm based on extremum and median value[J].Journal of Image and Graphics,2001,6(6):533-536.

[4]郭琳,尚振宏.一種有效的自適應中值濾波算法[J].長春工業大學學報:自然科學版,2008,29(1):87-90.GUO Lin,SHANG Zhen-hong.An effective adaptive median filter algorithm [J].Journal of Changchun University of Technology:Natural Science Edition,2008,29(1):87-90.

[5]錢偉新,劉瑞根,王婉麗.一種改進的自適應中值濾波算法[J].光學與光電技術，2011,9(4):35-38.QIAN Wei-xin,LIU Rui-gen,WANG Wan-li.An improved adaptive median filtering algorithm[J].Optics&Optoelectronic Technology,2011,9(4):35-38.

[6]姚文偉,張智斌.一種改進的自適應中值濾波方法[J].東華理工大學學報:自然科學版，2012,35(4):428-431.YAO Wen-wei,ZHANG Zhi-bin.An improved method of adaptive median filtering[J].Journal of East China Institute of Technology:Natural Science,2012,35(4):428-431.