一種抗混疊濾波器的設計

郭紅玉

（朔州職業技術學院 山西 朔州 036002）

濾波是指從混雜的信號中提取有用信息的過程。對于電力系統來講，隨著時間的延續，變化的電壓或電流將會以“波”的形式出現 。通過信號采集設備，把獲取到得波分類處理，轉換成為時間波形，即信號。在這個過程中，系統實現了對信號的濾波。濾波器是對采集到信號進行過濾處理的器件。

混疊現象是指對連續信號進行等間隔采樣時，如果不能滿足采樣定理，采樣后就會有頻率重疊現象，即高于采樣頻率和低于采樣頻率的信號混雜在一起。失真現象就出現了，而這種失真即為混疊失真。在統計、信號處理和相關領域中，混疊是指取樣信號被還原成連續信號時產生彼此交疊而失真的現象。當混疊發生時，原始信號無法從取樣信號還原。而混疊可能發生在時域上，稱做時間混疊，或是發生在頻域上，被稱作空間混疊。抗混疊濾波器一般指低通濾波器。濾波器可以分為低通濾波器、帶通濾波器、帶阻濾波器、高通濾波器、高阻濾波器。抗混疊濾波器可提高采樣頻率，使之達到最高信號頻率的兩倍以上，可限制信號的帶寬，使之滿足采樣定理的條件。

濾波器的應用領域非常廣泛。例如，采樣視頻系統中的信號混疊現象，當超出視頻頻段范圍的高頻信號通過數模轉換器的采樣過程混疊回視頻頻段時，就會產生混疊現象；隨著電力電子技術的不斷發展，電力電子裝置廣泛投入運行，因而有大量的高次諧波注入電網，產生了嚴重的諧波污染，對于工農業生產造成了嚴重的影響；在當代煤礦的電網中，由于大量大功率和非線性設備的應用，致使部分煤礦電網中的諧波含量已經遠遠超出國家標準；在自動控制、測控系統的數據采集過程中，不可避免地會有高頻干擾信號混雜在有用信號當中，當這些信號的數據采集頻率超過采樣定理所規定的范圍時，就會采集到一些不確定的信號并對有用信號造成干擾，即頻率混疊。因此，諧波的測試和信號分析就成了經常和必須的工作[1-5]。

為了最大程度地抑制或消除混疊現象對動態測控系統數據采集的影響，就需要用抗混疊濾波器對無用信號進行過濾處理。因為有源濾波器[6]的精度依賴于電阻和電容值的精度，因此精度相比無源濾波器得到充分提高，有源濾波器的應用越來越廣泛。

1 幾種常見濾波器的比較

濾波器是一種對信號有處理作用的器件或電路。隨著電子市場的不斷發展也越來越被廣泛生產和使用。常見的濾波器有巴特沃斯濾波器、貝塞爾濾波器、切比雪夫濾波器、橢圓濾波器等。

1.1 巴特沃斯濾波器

巴特沃斯濾波器是由英國工程師替芬·巴特沃斯于1930年提出的，也是最常用的一種電子濾波器，特別適用于低頻段。其特點是通頻帶響應平坦，無起伏，之后緩慢衰減到截止頻率點，最后接近－20ndB/decade的衰減率。從振幅對數對角頻率波特圖上觀察，從一邊界角頻率開始，隨著角頻率的增加振幅會逐漸減小，趨于無窮大。

對于n階巴特沃斯低通濾波器幅頻特性關系式如下：

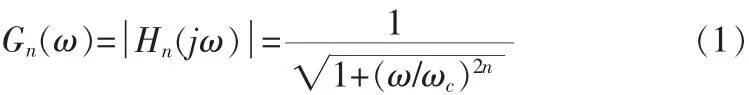
公式中：G是濾波器的放大率，H為傳遞函數，n是濾波器級數，ω是信號的角頻率，ωc為振幅下降3分貝時的截止頻率。令截止頻率時ωc=1，將對公式（1）進行歸一化有：

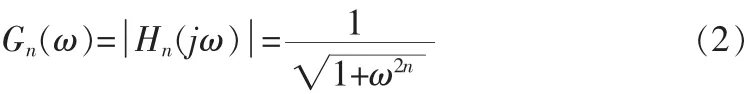
規一化的巴特沃斯多項式：

表1 歸一化的巴特沃斯多項式Tab.1 Normalized butterworth multinomial

1.2 貝塞爾濾波器

貝塞爾濾波器是由德國數學家弗雷德里希·貝塞爾提出的，是一種線性濾波器，其特點是延遲性，即具有最平坦的群延遲。在音頻系統中應用比較多。模擬貝賽爾濾波器在幾乎整個通頻帶都具有恒定的群延遲，因而在通頻帶上保持了被過濾的信號波形。

1.3 切比雪夫濾波器

切比雪夫濾波器是以俄羅斯數學家巴夫尼提·列波維其·切比雪夫命名的，由于能夠在通帶或阻帶上實現頻率響應幅度等波紋變動，又可分為“I型切比雪夫濾波器”和“II型切比雪夫濾波器”。其特點是在過渡帶呈現快速衰減，但頻率響應不及巴特沃斯平坦。切比雪夫濾波器和理想濾波器的頻率響應曲線之間的誤差最小，但是在通頻帶內存在幅度波動。

I型切比雪夫濾波器和II型切比雪夫濾波器相比應用較多，因為I型切比雪夫濾波器屬于通帶濾波器，而II型切比雪夫濾波器截至速度慢不常用。根據工作要求不同，如果需要快速衰減而允許通頻帶存在少許幅度波動，可用I型切比雪夫濾波器；如果需要快速衰減而不允許通頻帶存在幅度波動，可用II型切比雪夫濾波器。

1.4 橢圓濾波器

橢圓濾波器也叫考爾濾波器，特點是在通帶和阻帶呈現等波紋的。相比其他類型的濾波器，在階數相同的條件，橢圓濾波器有著最小的通帶和阻帶波動。這一特點是與巴特沃斯和切比雪夫最大的區別所在。

1.5 幾種常見濾波器的比較

下圖所示頻率響應圖分別為巴特沃斯濾波器、I型切比雪夫濾波器、II型切比雪夫濾波器及橢圓函數濾波器。

由圖可見，衰減速度最為緩慢平坦的是巴特沃斯濾波器，幾乎沒有幅度變化；I型切比雪夫濾波器、II型切比雪夫濾波器處于中等變化水平；橢圓函數濾波器呈現出較大的幅度波動。因此在選擇濾波器的時候，橢圓濾波器能夠以較低的階數獲得較窄的過渡帶寬，但是它在通帶和阻帶上都有波動。

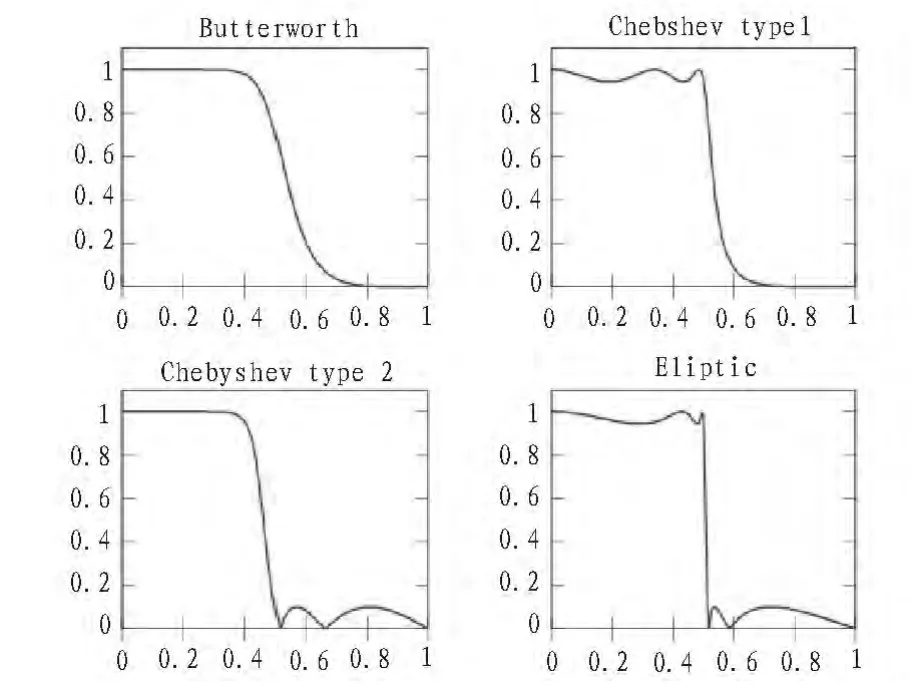
圖1 幾種常見濾波器頻率響應圖比較Fig.1 The compared with several filters

2 抗混疊濾波器的設計

抗混疊濾波器，采用二階巴特沃斯型帶通濾波器，這種類型濾波器的最大優點就是通帶衰減特性平坦。該濾波器可用于儀器儀表中的變換裝置，如用作頻譜分析儀中的選頻裝置。

2.1 濾波器的設計參數

1）中心頻率：245 kHz，帶寬：490 kHz（10～500 kHz）（其依據是后端AD轉換器的采樣率是1.6 MHz，為中頻信號帶寬的3倍）。

2）特征阻抗：50Ω。由于濾波器截止頻率較低，如果采用無源濾波器需要較大的電感，故采用Sallen－Key有源濾波器。有源濾波器其通帶內的信號不僅沒有能量損耗，而且還可以放大，負載效應不明顯，多級相聯時相互影響很小。

2.2 二階巴特沃斯型帶通濾波器的傳輸函數

圖2 二階巴特沃斯帶通濾波器傳輸函數Fig.2 2nd order band pass Butterworth continuous transfer function

2.3 二階巴特沃斯型帶通濾波器電路

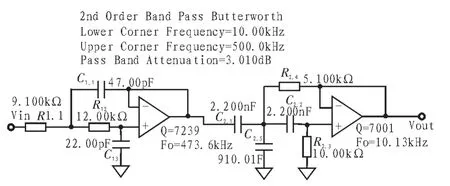
圖3 二階巴特沃斯型帶通濾波器電路Fig.3 2nd order band pass Butterworth circuit

2.4 二階巴特沃斯帶通濾波器響應

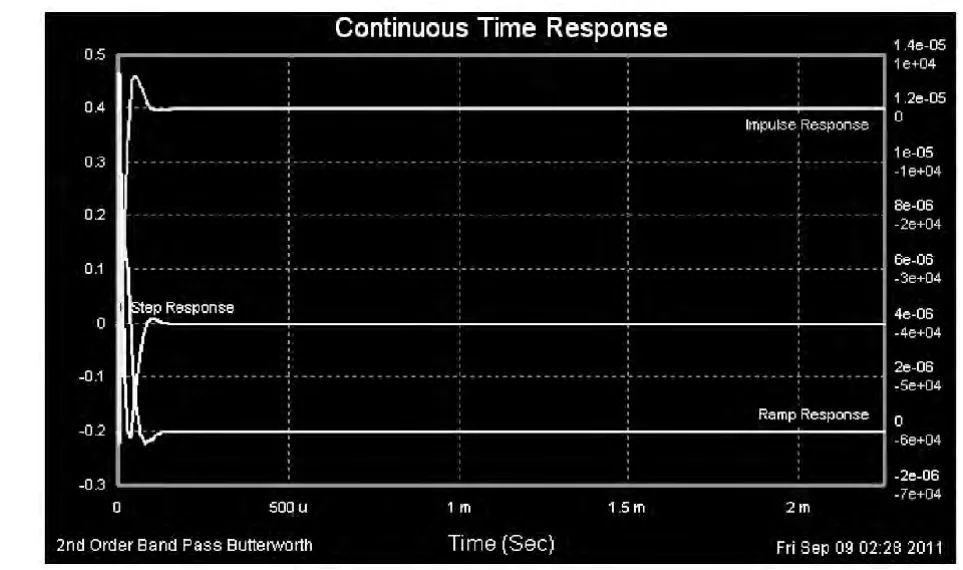
圖4 二階巴特沃斯型帶通濾波器的連續時間響應圖Fig.4 2nd order band pass Butterworth continuous time response

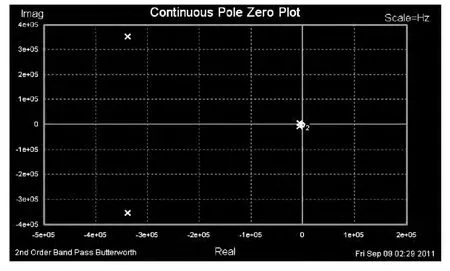
圖5 歸一化的二階巴特沃斯型帶通濾波器的零極點圖Fig.5 Normalized 2nd order band pass Butterworth continuous pole zero plot

3 結論

文中設計了一種基于二階巴特沃斯的帶通濾波器，該濾波器具有抗混疊特性，濾波結果平穩，能夠有效地將頻段內的信號輸出。利用Filter Solutions進行仿真，從仿真結果分析，實現了通帶衰減特性平坦，該濾波器可以有效消除信號混疊現象，使系統能夠穩定、可靠地對特定輸入信號進行采樣處理。

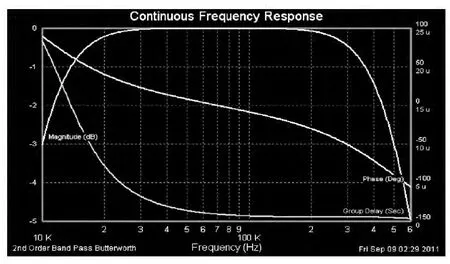
圖6 歸一化的二階巴特沃斯型帶通濾波器的頻率響應曲線Fig.6 Normalized 2nd order band pass Butterworth continuous frequency response

[1]文智江，朱名日.高頻信號直接采樣系統中的抗混疊濾波器設計[J].微型機與應用，2013，32（2）：28-33.WEN Zhi-jiang，ZHU Ming-ri.Design of anti-aliasing filer in direct sampling systemof high-frequency signal[J].Microcomputer＆ its Applications，2013，32（2）:28-33.

[2]彭永勝，王太勇，范勝波，等.高品質抗混疊濾波器設計[J].西南交通大學學報，2003，38（5）：596-601.PENG Yong-sheng，WANG Tai-yong，FAN Sheng-bo，et al.Design of high quality anti-aliasing filter[J].Journal of Southwest Jiaotong University，2003，38（5）:596-601.

[3]林祥金，張志利，朱智.Butterwort有源抗混疊濾波器設計[J].電子測量技術，2008，31（2）：66-69.LIN Xiang-jin，ZHANG Zhi-li，ZHU Zhi.Design of Butterworth active anti-aliasing filter[J].Electronic Measurement Technology，2008，31（2）:66-69.

[4]李偉濼，張龍.適應于有源電力濾波器的抗混疊濾波器設計[J].軟件，2012，33（1）：116-117.LI Wei-le，ZHANG long.Design of the anti-alias filter for active power filter[J].Software，2012，33（1）:116-117.

[5]李紹銘，張國利.用于電網諧波分析的抗混疊濾波器設計[J].華東冶金學院學報，2000，17（1）：42-45.LI Shao-ming，ZHANG Guo-li.Dseign of the anti-alias filter for the electric network harmonics analysis[J].Jof East China University of Metallurgy，2000，17（1）:42-45.

[6]葛帥.基于模糊控制的有源濾波器直流母線電壓控制[J].電子科技，2013（6）:25-27，30.GE Shuai.Active filter control dc bus voltage based on the fuzzy control[J].Electronic Science and Technology，2013（6）:25-27，30.