基于動態(tài)Kalman濾波的多傳感數(shù)據(jù)融合算法研究
吳耀+李文鈞+姜華+何風行


摘 要:提出一種基于動態(tài)Kalman濾波的多傳感器數(shù)據(jù)融合算法。首先通過模糊理論和協(xié)方差匹配技術(shù)對傳統(tǒng)的Kalman濾波算法中的噪聲協(xié)方差進行調(diào)整,使模型的噪聲更接近真實的噪聲水平,這在很大程度上提高了Kalman濾波器對模型變化的適應(yīng)能力。然后使用矩陣加權(quán)多傳感器線性最小方差意義下的最優(yōu)信息融合算法實現(xiàn)數(shù)據(jù)融合。最后通過仿真實驗驗證了本文所提出的算法優(yōu)于經(jīng)典的卡爾曼濾波算法。
關(guān)鍵詞:數(shù)據(jù)融合;噪聲協(xié)方差;卡爾曼濾波;傳感器
中圖分類號:TP274 ? ? ? ? ? 文獻標識碼:A ? ? ? ? ? ? ? ? ? ? 文章編號:2095-1302(2015)01-00-03
0 ?引 ?言
多傳感器數(shù)據(jù)融合結(jié)果的性能是一直存在的問題[1],針對這個問題的其中一個解決辦法是通過經(jīng)典卡爾曼濾波算法,它采用方差上界消除相關(guān)和統(tǒng)一的信息分配原則[2],避免了互協(xié)方差陣的計算來對多傳感器組合系統(tǒng)進行數(shù)據(jù)處理,后來又有人在此基礎(chǔ)上提出了極大似然融合估計算法[3-5],但是要求假設(shè)隨機變量服從正態(tài)分布,以便構(gòu)造似然函數(shù)。這在很大程度上提高了多傳感數(shù)據(jù)融合的準確度,但是,在實際的融合過程中經(jīng)典卡爾曼濾波器技術(shù)存在著難以克服的發(fā)散問題等,當觀測噪聲和過程噪聲不再是白噪聲時,濾波器就會變得不穩(wěn)定。
針對傳統(tǒng)的卡爾曼濾波器與系統(tǒng)模型的耦合度強、魯棒性差以及難以克服的發(fā)散問題[6,7],本人在研究了大量現(xiàn)有的數(shù)據(jù)融合算法的基礎(chǔ)之上,提出了一種基于動態(tài)卡爾曼濾波的多傳感器數(shù)據(jù)融合算法,在很大程度上提高了Kalman濾波器對模型變化的適應(yīng)能力,使濾波精度更高。最后通過仿真實驗驗證了本文所提出的算法優(yōu)于經(jīng)典的卡爾曼濾波算法。
1 ?系統(tǒng)總體概述
首先,假設(shè)存在N個不同的傳感器,它們的采樣率是一致的。多傳感器動態(tài)系統(tǒng)的模型可描述為:
X(k)=A(k)X(k-1)+B(k)P(k) ? ? ? ? ? ? ?(1)
Yi(k)=Zi(k)X(k)+Mi(k),i=1,2,…,N ? ? ? ? ? (2)
其中:k表示離散時間,X(k)∈Rn是系統(tǒng)的n維狀態(tài)向量,A(k)∈Rn是系統(tǒng)的狀態(tài)轉(zhuǎn)移矩陣,B(k)是噪聲與狀態(tài)向量之間的轉(zhuǎn)移矩陣,隨機向量P(k) ?表示狀態(tài)轉(zhuǎn)移時系統(tǒng)的高斯噪聲,且P(k) ?滿足:
E{P(k) }=0 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (3)
E{P(k)PT(s) }=Q(k)δks ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(4)
其中:E為數(shù)學期望,T為轉(zhuǎn)置,δkj為克羅內(nèi)克函數(shù)。
式(2)中i表示第i個傳感器,Yi(k)∈Rn為第i個傳感器的觀測向量,Zi(k)∈Rn為第i個傳感器的觀測陣,Mi(k)∈Rn為對應(yīng)傳感器的觀測噪聲,滿足均值為0的高斯分布,且M(k)滿足:
E{Mi(k)}=0 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(5)
E{Mi(k)MiT(s)}=Ti(k)δks ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(6)
其中:E為數(shù)學期望,T為轉(zhuǎn)置,δkj為克羅內(nèi)克函數(shù)。
2 ?經(jīng)典Kalman濾波描述
2.1 ?經(jīng)典Kalman濾波算法
1960年由卡爾曼首次提出卡爾曼濾波,Kalman濾波是一種線性最小方差估計。Kalman濾波理論在很多領(lǐng)域都得到了較好的應(yīng)用,阿波羅登月飛行和C-5A飛機導航系統(tǒng)的設(shè)計是早期應(yīng)用中的成功者。本文主要講述景點卡爾曼濾波算法在多傳感數(shù)據(jù)融合領(lǐng)域的應(yīng)用。
對于第一節(jié)中的系統(tǒng),經(jīng)典Kalman濾波算法描述為:
X(k)=X(k/k-1)+H(k)[Y(k)-Z(k)X(k/k-1)] ? ? (7)
X(k/k-1)=A(k)X(k/k-1) ? ? ? ? ? ? ? ? ?(8)
H(k)=r(k/k-1)Z(k)T[Z(k)r(k/k-1)Z(k)T+T(k)]-1 ? (9)
r(k/k-1)=A(k)r(k-1)A(k)T+B(k)Q(k)B(k)T ? (10)
r(k)=[I-H(k)]Z(k)r(k-1) ? ? ? ? ? ? ?(11)
2.2 ?線性最小方差加權(quán)數(shù)據(jù)融合算法
在線性最小方差意義下的多傳感器系統(tǒng),有如下加權(quán)數(shù)據(jù)融合定理。
定理1:已知有n個不同傳感器,它們的隨機向量Y∈Rn的N個無偏估計為Yi(k/k),i=1,2,…,n,且已知估計誤差的協(xié)方差陣為Pij,i,j=1,2,…,m,則按矩陣加權(quán)線性最小方差無偏融合估計Y0(k/k)為:
(12)
最優(yōu)加權(quán)陣Bi,i=1,2,…,m由下面的公式計算:
B=P-1e(eTP-1e)-1 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (13)
其中,P=(Pij),i=1,2,…,m是nm×nm的對稱正定矩陣,B=[B1,B2,…,Bm]T和e=[In,I2,…,In]T都是nm×m的矩陣。最優(yōu)融合估計誤差方差陣為:
P0=(eTP-1e)-1 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (14)
其中P0
3 ?動態(tài)Kalman濾波算法
對于第一節(jié)所描述的系統(tǒng),在線性最小方差意義下經(jīng)典卡爾曼濾波器給出了無偏融合估計。在過程噪聲和觀測噪聲的數(shù)學期望均為零且均為白噪聲的前提下,經(jīng)典卡爾曼濾波給出的系統(tǒng)狀態(tài)估計還算準確,與實際系統(tǒng)符合程度較高。但是,在實際的環(huán)境中,過程噪聲和觀測噪聲的協(xié)方差矩陣是不能準確知道的,而且一般情況下的過程噪聲和觀測噪聲也不再是白噪聲了,此時若還用經(jīng)典Kalman濾波,將會導致系統(tǒng)的狀態(tài)估計誤差非常大,甚至很容易導致濾波的發(fā)散,一旦出現(xiàn)濾波發(fā)散將會使數(shù)據(jù)融合失敗。
為了使系統(tǒng)的過程噪聲和觀測噪聲更符合實際情況,而不能提前就確定過程噪聲和觀測噪聲的協(xié)方差矩陣,因此,必須采取一定的措施來動態(tài)的估計以上兩種噪聲的協(xié)方差,從而提高濾波的精度,防止濾波的發(fā)散,修正系統(tǒng)狀態(tài)估計值,使得估計值與真實值較為接近。
本節(jié)主要研究通過協(xié)方差匹配技術(shù),增強殘差的理論協(xié)方差和實際協(xié)方差的一致性來實現(xiàn)。殘差u(k),可表示為:
u(k)=Y(k)-Z(k)X(k/k-1) ? ? ? ? ? ? ? ?(15)
殘差的理論協(xié)方差S(k+1) ,可通過下面的表達式計算:
S(k+1) =H(k+1) P(k+1/k) HT(k+1) +R(k+1) ? ? ? ? ?(16)
殘差的實際協(xié)方差F(k),可通過下面的表達式計算:
(17)
其中:K是經(jīng)驗參數(shù),表示用來計算實際協(xié)方差陣的窗口大小,一般取20左右。通過比較殘差的實際協(xié)方差和殘差的理論協(xié)方差的差值大小,采用模糊推理系統(tǒng)調(diào)整R(k) 來消除二者之間的差異,即:殘差的理論協(xié)方差和實際協(xié)方差基本一致時,不作調(diào)整。殘差的理論協(xié)方差大于實際協(xié)方差時,減小R(k) 的值。殘差的理論協(xié)方差小于實際協(xié)方差時,增大R(k) 的值。
FLS包括3個部分:模糊化、模糊控制規(guī)則生成以及反模糊化。模糊化是把輸入的精確量轉(zhuǎn)化成輸入的模糊量,而模糊控制規(guī)則生成是將輸入的模糊量通過推理生成輸出的模糊量,最后的反模糊化過程則把輸出的模糊量輸出轉(zhuǎn)化成精確量的輸出。反模糊化的主要方法有最大隸屬度法、重心法,其中,重心法是目前應(yīng)用較多的反模糊化方法,本文采用的就是重心法,其計算公式如下:
(18)
式中:α表示計算出的精確值,μ(αi)表示隸屬度函數(shù),αi表示模糊集合的元素。
圖1 ?動態(tài)卡爾曼濾波算法流程圖
4 ?實驗驗證
假設(shè)存在兩個傳感器,滿足以下的線性系統(tǒng):
(19)
(20)
其中: x1(k), x2(k)分別為k時刻輸入信號的狀態(tài)值, u1(k),u2(k)是線性不相關(guān)的且數(shù)學期望為零的高斯白噪聲序列,其協(xié)方差矩陣為Q=0.02I2;yj1(k),yj1(k)分別為第j個傳感器在k時刻對系統(tǒng)狀態(tài)的觀測值,vj1(k),vj1(k)分別為第j個傳感器的噪聲序列,為兩個傳感器的觀測矩陣。
為了方便比較,采用如下記號作為性能指標:
其中:Xi(k)與Xi(k/k)分別表示定位物體在k時刻的真實值和估計值。下表給出了經(jīng)典Kalman濾波和動態(tài)Kalman濾波仿真實驗均方誤差的比較:
表1 ?經(jīng)典卡爾曼濾波與動態(tài)卡爾曼濾波均方誤差的比較
均方誤差(Δi) Δ1 Δ2
經(jīng)典Kalman濾波 0.923 1 0.931 6
動態(tài)Kalman濾波 0.714 8 0.725 3
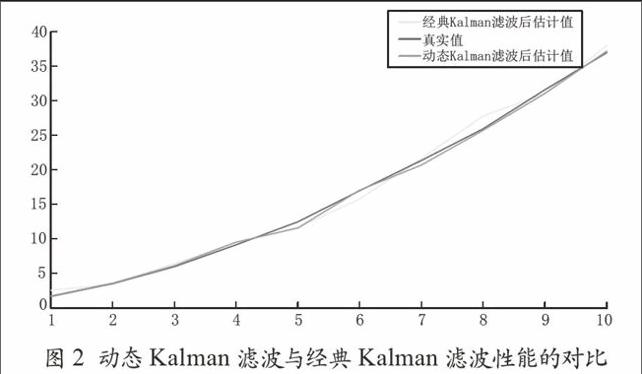
下圖給出了分別采取經(jīng)典Kalman濾波和動態(tài)Kalman濾波的兩種情形下系統(tǒng)狀態(tài)的最優(yōu)估計值與真實值的對比。
對本文提出的動態(tài)卡爾曼濾波算法和經(jīng)典卡爾曼濾波算法性能和誤差進行了對比,如圖2、圖3所示。在相同實驗室環(huán)境下,本文算法的最優(yōu)估計值與真實值更加接近且均方誤差<0.75。
圖2 ?動態(tài)Kalman濾波與經(jīng)典Kalman濾波性能的對比
圖3 ?動態(tài)Kalman濾波與經(jīng)典Kalman濾波均方誤差的對比
5 ?結(jié) ?語
針對實際情況下,過程噪聲協(xié)方差和觀測噪聲協(xié)方差不能事先確定這一問題。本文提出了一種基于動態(tài)Kalman濾波器的多傳感數(shù)據(jù)融合算法。通過協(xié)方差匹配技術(shù),增強殘差的理論協(xié)方差和實際協(xié)方差的一致性來實時地估計兩種噪聲的協(xié)方差。仿真實驗表明了,本文提出的算法是可行的也是有效的。當然這里還存在一個問題待以后繼續(xù)研究,即傳感器數(shù)量選擇問題,并不是傳感器數(shù)量越多越好,達到一定數(shù)量以后,任意增加個數(shù)可能還會有負面的影響。
參考文獻
[1] 王媛彬.多傳感器信息融合概述及其應(yīng)用[J].傳感器世界,2010(12):6-9.
[2] 李海艷,李維嘉,黃運保.基于卡爾曼濾波的多傳感器測量數(shù)據(jù)融合[J].武漢大學學報,2011,44(4):521-526.
[3] Bar-shalom,Y. On the track-to-track correlation problem[J]. IEEEE Transactions on Automatic Control,1981(2):571-572.
[4] 彭冬亮,文成林, 薛安克.多傳感器多源信息融合理論及應(yīng)用[M].北京:科學出版社,2010.
[5] Bar-Shalom Y, Li X R. Estimation and Tracking, Principles, Techniques, and Software[M]. Artech House, 1993.
[6] 郝凱,孟正大. 基于卡爾曼濾波的室內(nèi)服務(wù)機器人定位[J].華中科技大學學報,2008,36(1):193-195.
[7] 徐田來,游文虎,崔平遠.基于模糊自適應(yīng)卡爾曼濾波的INS/GPS組合導航系統(tǒng)研究[J].宇航學報,2005,26(5):571-575.
[8] Carlson N A, Berarducci M P. Federated Kalman filter simulation results[J]. Journal of the Institute of Navigation,1994,41(3):297-321.
[9] LeBlanck, Saffiotti. A Multi-robot Object Localization: A Fuzzy Fusion Approach[J]. IEEE Transon Systems, Man, and Cybernetics, PartB: Cybernetics, 2009,39(5):1259-1276.
[10] 徐琦,蔡聰,王熠釗. 一種基于數(shù)據(jù)融合的機動目標跟蹤預(yù)測算法[J].系統(tǒng)仿真學報,2011,23(11):2444-2448.
[11] 權(quán)義寧,姜振,黃曉冬,等. 一種新的數(shù)據(jù)融合航跡關(guān)聯(lián)算法研究[J].西安電子科技大學學報,2011,39(1):82-90.
[12] Hall L D. Mathematical Techniques in Multisensor Data Fusion[M]. Norwood, MA:Artech House,2002.

