偏心度與間隙比對軸流泵流動激勵力的影響

王玨星　楊愛玲　陳二云　戴韌　李國平

摘 要： 葉輪偏心將會引起軸流泵葉輪頂部間隙沿周向不均勻，從而導致附加的流動激勵和噪聲.利用計算流體力學商業軟件Fluent模擬不同偏心度和間隙比的軸流泵非定常流場，研究周向非均勻間隙對泵內壓強脈動及葉輪激勵力的影響.結果表明：壁面壓強脈動強度并不是在最小間隙處達到最大，而是出現在偏離最小間隙處約30°～60°的方向，并隨著間隙比增大，脈動強度最大值發生位置逐漸向最小間隙處靠攏；同時，偏心造成的非均勻葉頂間隙引起了軸頻處的壓強脈動，在間隙比為2.5%下偏心度從0%增加到60%，軸頻處的壓強脈動相對增量為661.54%；葉輪受到的徑向激勵力時均值與偏心度呈線性關系，其斜率與間隙比的平方根成正比.

關鍵詞：非均勻葉頂間隙； 偏心度； 間隙比； 壓強脈動； 葉輪激勵力

中圖分類號： TH 312 文獻標志碼： A

隨著流體機械以及渦輪機械載荷的不斷加大，軸系渦動現象日益顯著.軸系渦動導致葉輪頂部間隙沿周向呈非均勻分布，產生附加流動激振力，從而引起旋轉機械振動并輻射噪聲.這一問題已得到國內外學者的關注.

早在上世紀五、六十年代，Thomas[1]、Alford[2]對汽輪機及燃氣輪機的轉子偏心進行了研究，結果發現葉輪高速旋轉時會出現偏心現象，并且Alford導出了葉輪偏心引起的激振力公式，該力也被稱為Alford力.1984年Vance等[3]利用鼓風機進行的偏心實驗證實了Alford力的存在.1994年晏礪堂等[4-5]對偏心引起的自激力作了理論和實驗分析，研究表明自激力會推動轉子反進動.2006年唐云冰等[6]以Jeffcott轉子為例研究了葉輪偏心間隙引起的氣流激振力對轉子穩定性的影響規律.2008年黃來等[7]通過數值模擬方法分別對不同間隙、偏心度、轉速對氣流激振力的影響進行了研究.2011年游磊等[8]對軸流泵振動加速度作了監測，證實轉速為960 r·min-1時存在軸偏心和葉輪偏心.

國內外公開發表的研究資料[9]表明，葉輪在旋轉時會出現偏心現象，且這種葉輪偏心引起的周向葉頂間隙不均勻性會隨著葉片載荷的增加而增加.學者們對汽輪機的轉子偏心間隙問題高度關注，并開展了深入細致的研究.然而，關于因轉子偏心導致的周向非均勻葉頂間隙對軸流泵性能與流動激勵力的影響的研究十分匱乏.本文利用數值方法模擬在不同偏心度、間隙比下葉頂非均勻間隙對軸流泵殼壁靜壓脈動以及激勵力的影響，以期對今后研究水泵振動以及噪聲問題有所幫助.

1 幾何模型及數值求解方法

1.1 軸流泵幾何參數

本文研究的軸流泵葉輪輪轂半徑R1=66.67 mm、葉輪葉頂半徑R2=125 mm、葉片數Z=4、額定轉速n=960 r·min-1、額定流量Qs=300 m3·h-1.圖1為軸流泵葉輪幾何參數示意圖，其中：δ0為初始均勻葉頂間隙；e為葉輪偏心量；h為葉高.葉輪在工作過程中，由于轉軸渦動及流體不平衡力作用，葉輪可能偏離中心位置，形成周向不均勻的葉頂間隙.在實際情況下，e在葉輪工作過程中一直隨時間變化，直接采用數值方法模擬葉輪偏心運動過程帶來的非均勻葉頂間隙時，需不斷計算葉輪位置并生成新的旋轉葉輪及間隙區域網格，需模擬的時間物理尺度包括偏心運動周期和葉輪旋轉周期，這些都存在較大的困難.本文對模型進行了簡化，忽略葉輪偏心運動的動力特性，在不同偏心度下模擬軸流泵流場，對比分析非均勻葉頂間隙對軸流泵水力性能、流動非定常激勵力的影響.表1給出了本文模擬葉輪偏心的模型參數，其中：J為間隙比，為δ0與h的比值；P=e/δ0，為偏心度，用于衡量非均勻葉頂間隙的程度，P=0%對應于葉輪位于泵管中心的狀態.

1.2 計算域及計算網格

圖2為軸流泵模型的計算域示意圖，其中：r為徑向軸；z為軸向軸；ω為葉輪旋轉角速度；D2為管徑.為了簡化幾何模型，忽略了軸面幾何細節，并在葉輪前、后分別加了一段長為6倍管徑的延長段.計算域由葉輪域、間隙域、進口延長域和出口延長域4部分組成，其中葉輪域為旋轉域，其它域為靜止域.

計算域采用結構網格進行離散，總體網格數約162萬，其中：葉輪域網格數為101萬；間隙

域網格數為18萬；進、出口延長域網格數均為22萬左右.圖3～4分別為葉輪域和間隙域網格軸向視圖及其中的局部放大圖，圖3中A為葉輪域和間隙域交接處；B為葉輪葉根前緣處.

1.3 數值計算方法及邊界條件設置

軸流泵的工質為水，在常溫常壓下一般視為不可壓液體.因此，本文采用三維不可壓的雷諾時均N-S方程組作為定常流場的控制方程，相應的湍流模型為k-ε RNG模型，流場迭代求解采用SIMPLEC壓力速度耦合方法.將獲得的定常流場收斂解作為初場，采用大渦模擬方法計算軸流泵內的非定常場，從而獲取泵內壓強脈動與激勵力信息.在非定常計算中，時間步長ΔT=T/360，T為葉輪旋轉周期.每迭代一個時間步長，相當于葉輪旋轉了1°.采用該時間步長，流場脈動信號中最高分辨頻率f不小于2 880 Hz（f=1/（2ΔT）），遠高于葉片通過頻率64 Hz.

軸流泵的流場邊界條件主要有3類：進口邊界、出口邊界及固壁邊界.進口邊界以質量流量的進口方式給定，該方式在已知進口流量的情況下相比速度入口更為方便，因為不需要考慮進口截面上的速度分布.在出口壓強未知的情況下采用自由出流條件，出口邊界條件為默認流體出口處流動已充分發展，法向速度梯度為零.計算中，無論是靜止固壁（殼壁）還是運動固壁（葉片表面、軸面），均采用無滑移邊界條件，即相對固體壁面流體的法向與切向速度等于零.對計算域動靜交界面的處理，本文在定常計算中采用多重坐標系，而在非定常計算中采用滑移網格.

1.4 網格無關性驗證

為了確定網格的總體尺度，本文分別選取94萬、123萬、162萬、205萬等4種網格數，在相同的轉速、湍流模型以及邊界條件下對軸流泵性能進行計算.

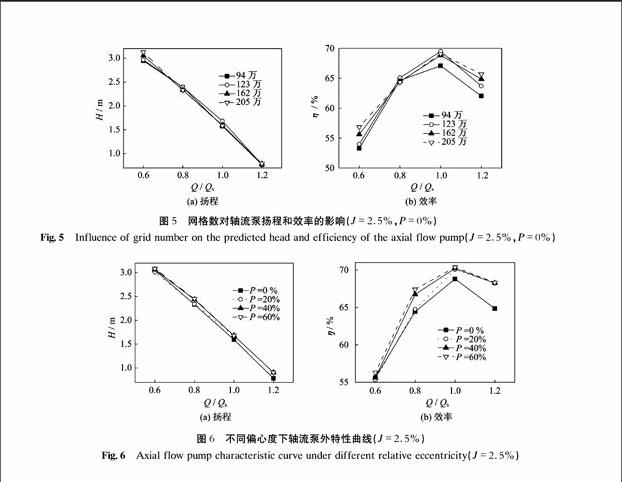
圖5給出了間隙比為2.5%、葉輪處于泵體中心（即P=0%）時網格數對水泵揚程H和效率η的影響.圖中橫坐標為無量綱流量，例如Q/Qs=1.0表示額定流量.需要說明的是，這4種網格數僅考慮了葉輪域網格的疏密變化，其它計算域的網格數保持不變.從圖5可知，隨著網格數增加，水泵揚程和效率均逐漸增加，但增加趨勢逐漸放緩.在額定流量下，網格數從94萬增加到205萬，η增加了3%；從162萬增加到205萬，η僅增加了0.26%，增加幅度明顯減小.可見，選擇162萬和205萬網格數均可滿足計算要求，但采用這4種網格數在相同的并行計算機上獲得收斂數值解的計算時間分別為4、6、7、11 h左右.如果進行非定常計算，獲得穩定的非定常流場解所需時間是相應定常計算時間的20多倍.綜合數值解準確度和計算效率兩方面因素，本文后續的軸流泵模型在相同的網格劃分方式下，網格數均控制在162萬左右.

2 計算結果及分析

2.1 不均勻葉頂間隙對軸流泵水力性能的影響

圖6（a）、（b）分別給出了間隙比為2.5%不同偏心度的揚程和效率.隨著葉頂間隙的不均勻程度增加，小流量情況下揚程和效率幾乎未受影響，而在大流量情況下揚程和效率均受到一定影響，并且隨著葉頂間隙的不均勻程度增加，揚程和效率均有所增加.以額定工況下Q/Qs=1.0為例，從偏心度0%增加至60%，H增加了5.43%，η增加了1.58%.

2.2 不均勻葉頂間隙對殼壁壓強脈動特性影響

為了分析不均勻葉定間隙對軸流泵內非定常流場的影響，在不同的間隙比和偏心度下計算了軸流泵非定常流場，計算工況為軸流泵額定工況.圖7給出了軸流泵殼體壁面上24個監測點的分布，相鄰監測點間的周向夾角均為15°.

式中：p為每個監測點的瞬時靜壓；paver為監測點的脈動靜壓時均值；ρ為密度；ΔT為每個計算時間步長，本文取ΔT=1.736 111×10-4 s；T為整個計算時間，本文的T為葉輪旋轉3圈對應的時間，即T=0.187 5 s.

圖8（a）、（b）給出了J=2.5%、P=60%時1、3、5、21、23等5個監測點的壓強脈動系數Cp在頻域的分布.圖8（a）的橫坐標為無量綱頻率，其中fz為葉頻（本文軸流泵旋轉速度為960 r·min-1，葉片數為4，fz=64 Hz）.可見，各監測點的壓強脈動在頻譜上均表現出明顯的離散頻譜特性，極大值對應于葉片通過頻率及其諧頻，一階葉頻處的壓強脈動系數峰值最大，且最大峰值出現在監測點5處，大小為0.161 3，如圖8（b）所示.

為了說明偏心度對葉頻處壓強脈動的影響，圖9（a）、（b）給出了間隙比分別為2.5%和5.0%時1、3、5、21、23等5個監測點的一階葉頻峰值隨偏心度的變化.從圖可知，間隙比從2.5%增加到5.0%時，各監測點在葉頻處的脈動幅值減小了約10%～12%，最大脈動幅值點由監測點5向最小間隙處靠攏，監測點3的幅值達到最大.在同一間隙比下，各監測點葉頻峰值隨偏心度的變化規律并不一致.

圖10為J=2.5%時軸頻附近各點壓強脈動分布.隨著偏心度從0%增加到60%，監測點1的壓強脈動在軸頻下的峰值增加了661.54%，如圖10（d）所示.可見，隨著偏心度增大，軸頻（f/fz=0.25）附近壓強脈動開始顯著變化，軸頻處幅值越來越大.這是由于從均勻間隙轉變為非均勻葉頂間隙時，周向葉頂間隙的中心對稱性被打破，因而造成軸頻處出現壓強脈動，且隨著偏心度的增大，軸頻最大值出現在最小間隙處，即監測點1的位置，大小為0.013 2.

圖11給出了間隙比分別為2.5%和5.0%時，不同偏心度下軸流泵殼體內壁面監測點的壓強脈動強度的分布.從圖可看出，無論J=2.5%還是J=5.0%，最小間隙處（監測點1）的脈動強度均大于最大間隙區（監測點13），且殼壁上半圈（監測點1至13點）的脈動強度普遍大于殼壁下半圈（監測點13至24），這是由于葉輪旋轉造成的非均勻間隙流道非對稱效應.由于葉輪旋轉，在間隙區上部流道逐漸減小，為膨脹過程，而下半圈正好為壓縮過程.同樣的原因，殼壁脈動強度最大處并不出現在最小間隙處，而是在上半圈偏離最小間隙處約30°～60°處（監測點3至5點）.圖11還表明，隨著間隙比從2.5%增加到5.0%，各偏心度下的最大脈動強度減小.這表明隨葉頂間隙增加，間隙內流動由于偏心引起的膨脹和壓縮效應減弱，此時，最大脈動強度位置也向最小間隙處偏移.

2.3 葉輪激勵力分析

由于在未偏心時，葉輪流動參數呈周向對稱，因而徑向力約為零.隨著偏心度增加，存在徑向不平衡，使得徑向力變大.圖12給出了不同間隙比時徑向激勵力時均值隨偏心度的變化.從圖可知看，當J=2.5%，偏心度分別為0%、20%、40%、60%時，葉輪受到的時均徑向激勵力Fr分別為0.295、5.398、10.518、17.225 N；當J=5.0%，Fr分別為0.273、7.775、16.455、24.365 N.若以線性規律擬合數據，當J=2.5%，直線斜率為0.282；當J=5.0%，斜率為0.402，其斜率變化規律與間隙比的平方根成正比.

對間隙比J=2.5%的軸流泵模型的徑向力Fr時域信號進行傅里葉變換，不同相對偏心比下徑向激勵力頻譜圖如圖13所示.從圖可看出，隨著偏心度P不斷增加，徑向力的軸頻信號（f/fz=0.25）幅值也不斷增加，且隨著偏心度的增加，徑向力Fr主要頻譜峰值出現在f/fz=1.6，即約102 Hz處.

3 結 論

本文利用Fluent軟件對不同偏心度和間隙比的軸流泵模型進行了模擬計算，研究結果表明：

（1） 從殼壁的壓強脈動強度分布規律看，無論間隙比為多少，最小間隙區的壓強脈動強度均大于最大間隙區.但最小間隙處（監測點1）并不是壓強脈動強度最大處，而是在距最小間隙約30°～60°左右（監測點3至監測點5段內）的非均勻葉頂間隙膨脹區.隨著間隙比增大，最大壓強脈動強度向最小間隙處偏移.

（2） 因未考慮葉輪質心運動，故從頻譜上看，殼壁的脈動表現出明顯的離散頻譜特性，且極大值對應于葉片通過頻率和其諧頻.但葉輪在旋轉偏心時所帶來的非均勻葉頂間隙會對泵內流場在軸頻處壓強脈動產生影響.隨著葉頂間隙的非均勻程度增大，即隨偏心度增大，軸頻下壓強脈動增加，且增幅遠大于葉頻處的脈動增幅.

（3） 葉輪徑向激勵力的時均值與偏心度成正比，其斜率則與間隙比的平方根成正比，且隨著偏心度的不斷增加，徑向力的軸頻信號幅值也不斷增加.

參考文獻：

[1] THOMAS H J.Unstable natural vibration of turbine rotors induced by the clearance flow in glands and blading[J].Bull.de lAIM，1958，71（11/12）：1039-1063.

[2] ALFORD J S.Protecting turbomachinery from selfexcited rotor whirl[J].Journal of Engineering for Gas Turbines and Power，1965，87（4）：333-343.

[3] VANCE J M，LAUDADIO F J.Experimental measurement of Alfords force in axial flow turbomachinery[J].Journal of Engineering for Gas Turbines and Power，1984，106（3）：585-590.

[4] 晏礪堂，洪杰，李其漢，等.壓氣機葉輪偏心引起的自激力和穩定性的理論分析[J].航空動力學報，1994，9（2）：157-160.

[5] 晏礪堂，洪杰，李其漢，等.壓氣機葉輪偏心引起的自激力和穩定性的實驗研究[J].航空動力學報，1994，9（2）：161-164.

[6] 唐云冰，高德平，羅貴火，等.葉輪偏心引起的氣流激振力對轉子穩定性影響的分析[J].航空學報，2006，27（2）：245-249.

[7] 黃來，駱名文，丁學俊，等.葉輪偏心間隙氣流激振力的數值模擬[J].流體機械，2008，36（4）：19-21.

[8] 游磊，方方，李平勇，等.軸流泵振動加速狀態監測診斷系統的研究與設計[J].四川大學學報，2011，43（S1）：236-239.