鋼結構企業多項目調度的混沌粒子群算法優化研究

雷兆明 ，李秀婷，花季偉，王東澤

（1.河北工業大學 控制科學與工程學院，天津 300130；2.天津師范大學 計算機與信息工程學院，天津 300387）

隨著近年來科技的高速發展，鋼結構產品越來越受到人們的青睞，大多數的鋼結構企業所接收的項目不再單一，且客戶要求各有不同，不同的項目對鋼結構企業的人力、資源、工期以及鋼構件要求各有差異，企業想要在各個不同項目執行中最大限度的滿足客戶需求且使企業效績最優，就必須將多項目調度問題作為企業調度管理的重中之重[1]。

目前，對于以上提到的問題，許多學者紛紛提出了切實有效的辦法。文獻[2]提出一種緩存更換搜索算法（CRS-PSO），將基本算法和緩存的概念設計在一起，有效地解決了收斂速度慢的問題。文獻[3]使用混沌粒子群算法結合混合優先規則優化多項目管理問題，對項目管理中的柔性資源受限問題提出了較好的解決辦法。文獻[4]嘗試開發新的數學模型和一個標簽化的啟發式搜索方法作為方案解決多項目調度問題。本文針對傳統的粒子群優化算法易陷入局部收斂的特性，提出將混沌擾動加入算法流程，并對粒子的速度位置進行改進，進而在資源約束的情況下，對鋼結構企業多項目調度問題進行優化。

1 鋼結構多項目調度優化模型描述

一個典型的鋼結構多項目調度問題可描述為企業有Q個獨立的項目，每個項目均包含不同鋼構件數的工作，即第i個項目包含Qi件工作；每件工作有不同或相同的工序，每個工序使用不同或相同的資源，在資源庫中有R種資源，每種工序加工時間固定， j∈［1，Qi］，i∈［1，Q］。 針對所述問題，采用取最小方差的方法進行建模。要求鋼構項目資源分配均衡，并且要根據項目的優先級來合理分配資源。

式中：T為所有鋼構項目的總的預定完成工期；Rk為第k種資源的總量；Rk（t）為第t個工作日所有鋼構項目對第 k 種資源的需求量；Rij，k（t）為第 i個鋼構項目中第j件工作的工序在第t個工作日對第k種資源的需求量；φ為各個鋼構項目的優先級權重；φi為第i個鋼構項目的權重。

模型約束條件如下：

第i個鋼構項目中第j件的工序在t時刻的資源消耗量必須小于該資源的供應量。

保證t時刻進行的工序沒有超出工期范圍：

保證決策變量為正整數：

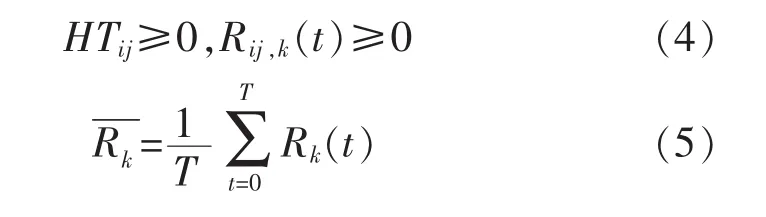
式中：Tij為第i個鋼構項目第j件工序的開始時間；dij為第i個鋼構項目第j件工序的持續時間；HTij為第i個鋼構項目第j件工作工序總富余時間；Uij為所有緊前工作的緊前工序集；TUij為第i個鋼構項目第j件工序的緊前工序開始時間；dUij為第i個鋼構項目第j件工序的緊前工序持續時間；Rk為第k種資源的平均需求量。

考慮到不同鋼構項目的重要程度不同，所有鋼構項目權重表示如下：

2 基于混沌粒子群的鋼結構企業多項目調度算法

2.1 局部模型和全局模型的統一粒子群算法

通過對鳥群捕食行為和自然群聚的研究，文獻[5-6]中提出了微粒群優化算法PSO（particle swarm optimization）。

在n維搜索空間中，將全局粒子群與局部粒子群相結合，粒子速度更新公式變為

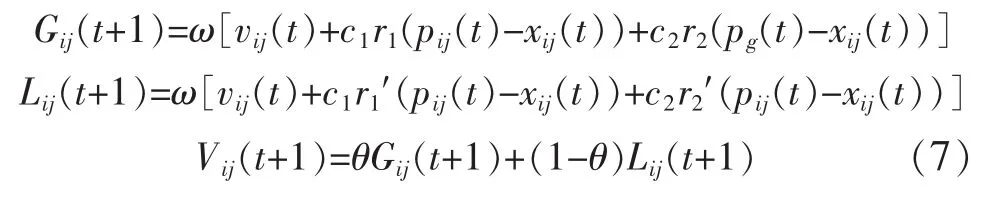
式中，Gij（t+1）和 Lij（t+1）分別是全局/局部版本的速度更新公式，θ是統一模型參數（0≤θ≤1），用于調整全局粒子群與局部粒子群搜索能力，本文采用動態θ值。位置更新公式為

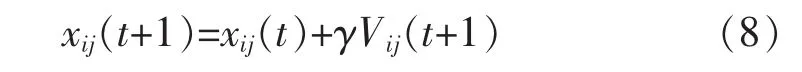
式中：ω為慣性權重；c1和c2為學習因子，值通常為2；r1和 r2為［0，l］之間的不同隨機數；γ 為約束因子，通常設置為1[7]。為了防止粒子飛行時脫離規定范圍，通常設置 Vij∈［-νmax，νmax］，Xij∈［-xmax，xmax］。

2.2 混沌改進的統一粒子群（CPSO）算法

混沌變量在粒子群運動過程中起到控制粒子混沌程度的作用[8]。典型的混沌系統（Logistic方程）為

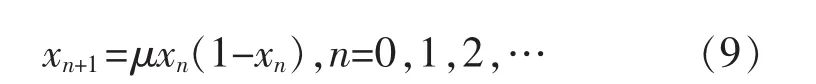
式中描述的是第n代與第n+1代間的邏輯關系，μ為控制參量；x為狀態變量；xn記錄第n代的狀態，xn∈［0，1］，0≤ μ≤4。

在統一粒子群中應用混沌進行粒子搜索，混沌擾動設在gbest鄰域進行，基本步驟如下：

1）由式（9）產生l個軌跡不同的混沌變量Yi=（yi1，yi2，…，yin），1≤i≤l；

2）將Xi的各個分量載波到混沌擾動范圍［-η，η］，擾動量 Δy=（Δy1，Δy2，…，Δyn），且 Δyj=-η+2ηYij，ynew=gbestk+Δy；

3）計算 f（ynew），若 f（ynew）＜ f（gbestk），則 gbestk=ynew。

2.3 早熟處理機制

粒子在搜索過程中易出現早熟現象，采用適應度方差來判斷粒子早熟，建立早熟處理機制，具體方法如下：

1）將粒子 Xak（k=1，…，n）按下式映射：

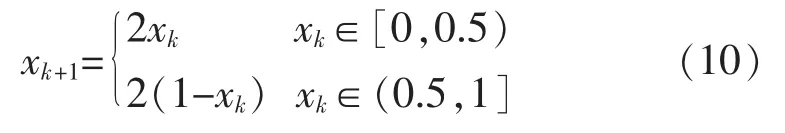
2）設迭代次數為N，產生混沌序列：

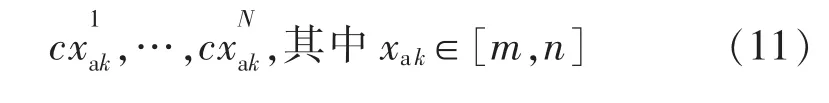
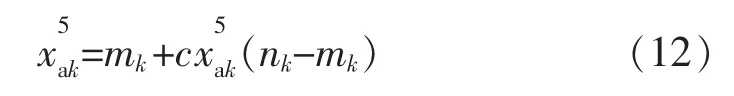
4）Xa經Tent映射后得到的新的混沌點列：

2.4 算法的編/解碼方式

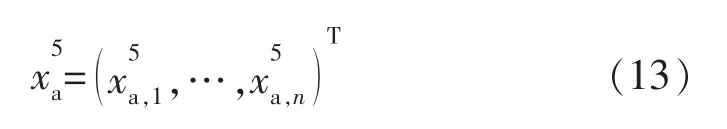
對于鋼結構企業多項目調度問題，本文提出一種適用于粒子群算法的項目編解碼方法，將各項目和項目中工序的排序在編碼中表示出來，優先值賦予公式為

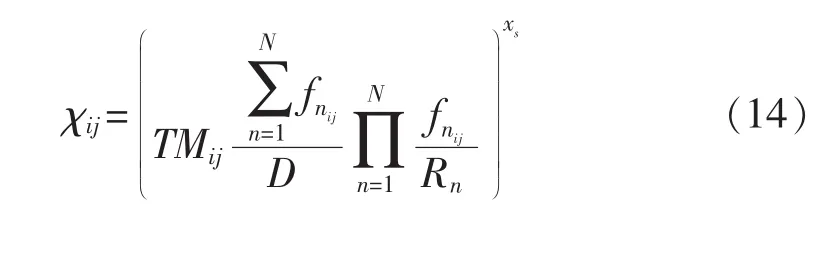
設置總工序數為n，項目數為s，以n維的實數向量表示粒子的狀態，編/解碼的過程如下：

1）隨機生成1～s+1間n個任意實數向量表示粒子的狀態；

2）對此n個實數向量進行分類，其中小數第一位相同的為一組；

3）在同一組中，按照實數向量的小數部分第二位的大小進行排序，形成鋼結構項目工序的調度順序。

假設某鋼結構企業現有3個項目，總共8道工序，采用上述編碼方式如下：

P：（1.12，3.14，5.11，7.13），（2.23，3.21，4.25，6.21），（1.31，2.34，3.32，6.31，8.32）表示 3 個不同項目。 按上述解碼方法，將P中小數第一位相同的分在同一組，得 X=（1.12，1.31，2.23，2.34，3.21，3.14，4.25，4.32，5.11，6.21，6.31，7.13，8.32）；然后，在每個分組內，按照P小數部分第二位從大到小排列，得到X=（1.12，1.31；2.34，2.23；3.14，3.21；4.25，4.32；5.11；6.21，6.31；7.13；8.32）。 將上述狀態映射到對應的鋼結構項目中，即可生成這組編碼對應的優先規則方案 Y=（1，3，3，2，1，2，2，3，1，2，3，1，3）， 表示第一個安排項目一中的工序，第二個安排項目三中的工序，第三個安排項目三中的工序，以此類推。

在上述編碼方式中，項目總工序的數與粒子維數相當，只需進行一次排序和取整運算即可解碼，對于像鋼結構多項目這樣的大規模問題，可以節約計算時間。此編碼方式與混沌粒子群相切合，可以使用其已有規則，更快獲得最優解。

2.5 算法優化調度流程

根據上面對混沌粒子群算法優化調度問題的描述，算法流程如圖1所示。

3 算例分析

以某鋼結構企業多項目調度問題為例，設定有8種不同資源，10種不同工序，各工序間有緊前緊后約束時間，不同項目間有相同工序，不同工序也可使用同種資源，各項目在所需工序后面顯示編號，不需要則顯示0，具體情況如表1所示。

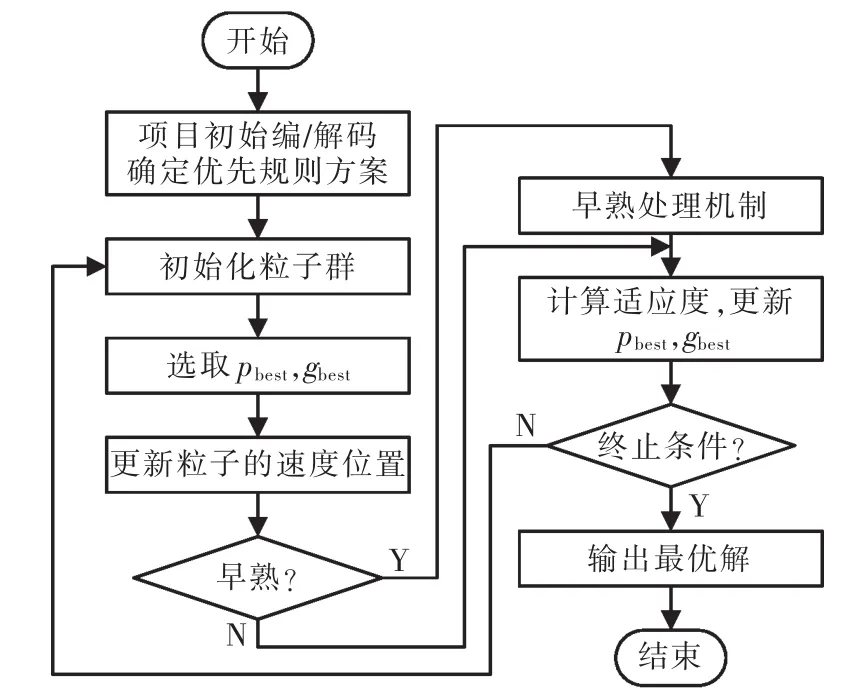
圖1 算法流程Fig.1 Flow chart of algorithm process

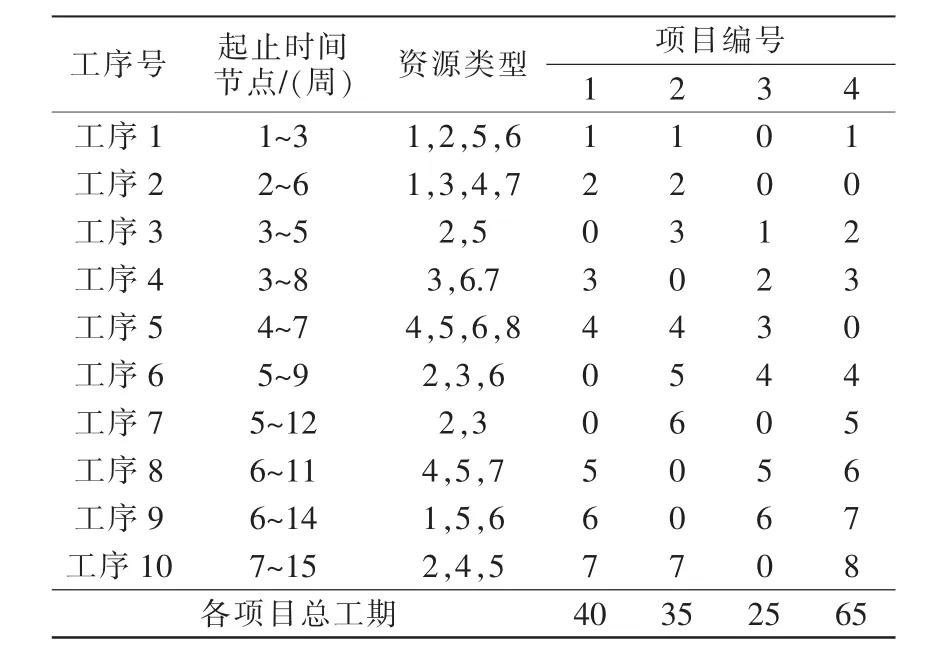
表1 各項目所需資源類型及時間約束Tab.1 Project resource types and time constraints

為了說明本文算法的有效性，經編/解碼計算，優先規則方案為 Y=（2，1，2，4，3，1，2，2，4，4，3，1，4，1，3，4），分別使用PSO、CPSO對調度問題進行優化。參數設置如下：種群規模50；最大迭代次數350；慣性因子ω=0.95；學習因子c1=c2=2；統一模型參數θ=0.78；CPSO的種群適應度方差σ2=0.5。每種參數下均隨機運行40次，得到結果如表2所示，仿真圖如圖2所示。

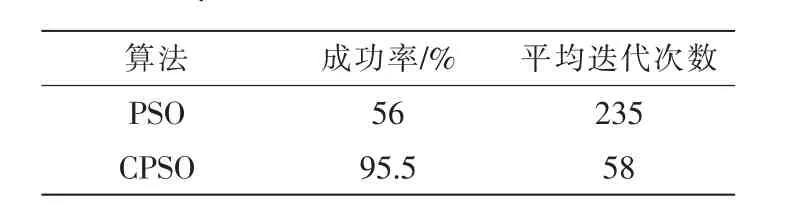
表2 PSO、CPSO運算結果比較Tab.2 Comparison results of PSO and CPSO

圖2為該多目標算例分別在基本粒子群算法和改進后的混沌粒子群算法所得到的平均最優適應值曲線圖，即收斂圖的比較。可以看到，PSO算法在求解該項目調度問題時，需要進行219次迭代才能達到收斂效果，且容易出現局部收斂現象，而改進的混沌粒子群算法只需52次迭代運算即可達到收斂，由此可見CPSO算法收斂性更好，全局收斂能力強，速度快且結果比較穩定。

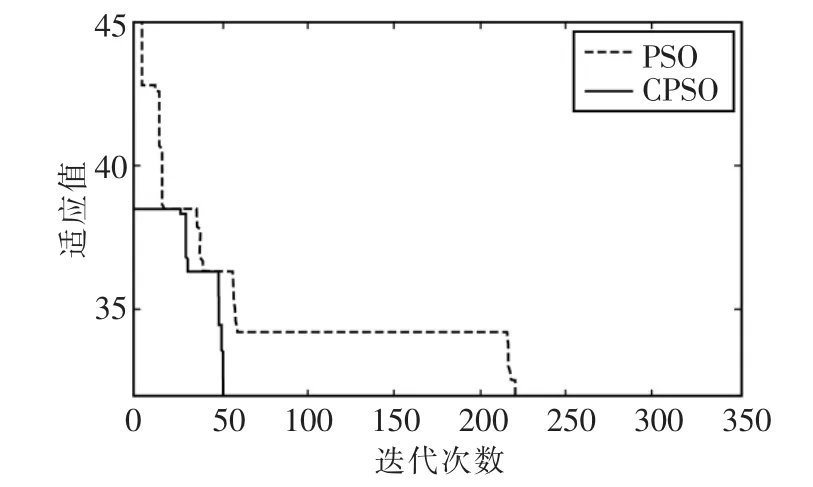
圖2 PSO、CPSO收斂性分析Fig.2 Convergence analysis of PSO and CPSO

4 結語

針對PSO存在著精度較低，易陷入局部收斂等缺點，利用混沌變量的隨機性，遍歷性，本文提出了使用統一粒子群優化算法與混沌相結合的改進思想。仿真結果表明，改進后的算法較好地克服了標準粒子群優化算法的缺點，尤其是在防止種群陷入局部最優點上取得了很好的效果。將該優化算法用于求解多項目管理優化調度問題，能夠較好地兼顧計算速度和結果精度，并且能夠合理地處理約束條件，為多項目管理調度問題的優化提供了一條有效的途徑。

[1]趙海洋.多項目協同管理系統的設計與實現[D].陜西：西北大學，2013.

[2]Mingyue Feng，Hua Pan.A modified PSO algorithm based on cache replacement algorithm[J].Computational Intelligence and Security（CIS），IEEE Con.2014，558-562.

[3]陳君蘭，葉春明.柔性資源受限多項目調度的混沌粒子群算法研究[J].計算機應用研究，2013，30（1）：117-120.

[4]Roshanaei V，Ahmed Azab，ElMaraghy H.Mathematical modelling and ameta-heuristic forflexible job shop scheduling[J].International Journal of Production Research，2013：6247-6274.

[5]Kennedy J，EberhartR C.Particle swarm optimization[C]//Proceeding of 1995 IEEE International Conference on Neural Networks，New York，1995：1942-1948.

[6]Eberhart R C，Kennedy J.A new optimizerusingparticle swarm theory[C]//Proceedings of the Sixth International Symposium on Micro Machine and Human Science，New York，1995：39-43.

[7]曾建潮，介婧，崔志華.微粒群算法[M].北京：科學出版社，2004.

[8]胥小波，鄭康鋒，李丹，等.新的混沌粒子群優化算法[J].通信學報，2012，33（1）：28-34，41.