基于大數據的多尺度系統軟測量方法及其應用

楊 彬

（中環天儀股份有限公司，天津 300384）

隨著信息技術的進步，大數據的存儲和使用成為可能，將基于大數據的分析方法用于軟測量中，可以實現多種難以測量或者暫時不能測量的重要參數的檢測。

論文在定義多尺度系統的基礎上，提出一種基于大數據的軟測量方法，并將之用于鍋爐輻射受熱面灰污程度的軟測量。

目前輻射受熱面灰污監測的方法主要有加裝熱流計，測量各點的熱流量反映其灰污程度[1]；采用傳熱學理論計算以實現灰污監測[2]；采用數值模擬的方法計算爐膛內溫度場的分布狀況，獲得受熱面的灰污程度等[3]。然而當前的方案或存在投資成本高、維護困難的問題，或存在部分重要參數，如火焰中心位置、煤質等，在目前的技術水平下無法測量的問題[4-8]，因此上述監測方法難以獲得令人滿意的效果。

采用本文提出的算法，可以在一定程度上解決輻射受熱面灰污程度的軟測量問題，為進一步的吹灰優化等提供技術依據。

1 多尺度系統

對一個非線性時變系統：Y=f（U，t）將輸入 U、輸出Y做k尺度小波變換，um∈U，yn∈Y可分解為細節分量重構信號 um1、um2…umj，yn1、yn2…ynj， j=1，…，k，以及近似分量重構信號 uma、yna，定義：

um、yn的第j尺度細節分量重構信號能量pdet（umj）、 pdet（ynj）為

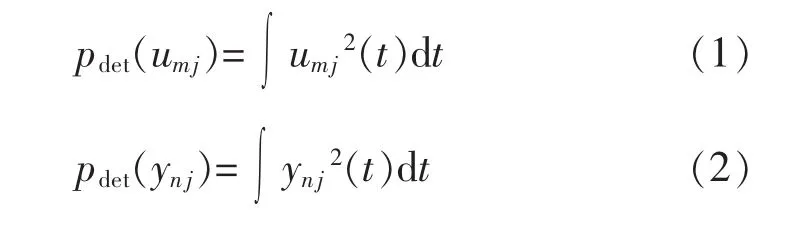
um、yn的第j尺度近似分量重構信號能量papp（uma）、papp（yna）為

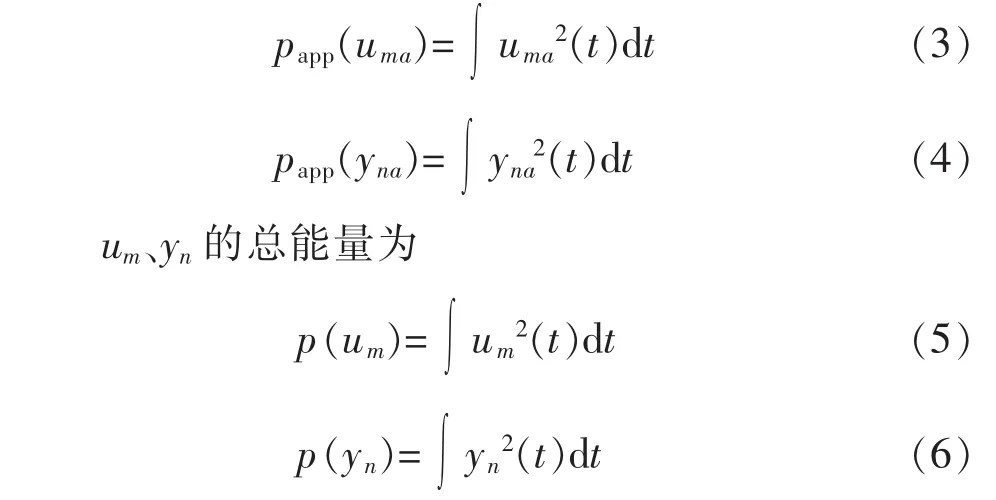
um、yn的細節分量重構信號能量與近似分量重構信號能量代表了系統變量分布在不同尺度下的能量，其大小表明參數在此尺度上分布的強弱。

基于上述信號能量，可以定義um、yn的多尺度相對能量矩陣A、B如下：

多尺度相對能量矩陣A、B分別表明了輸入、輸出變量分布在不同尺度下的分量間強弱關系，利用多尺度相對能量矩陣A、B，可以定義多尺度系統如下：

當0＜∑aij＜∞時，說明系統的輸入在每一個尺度上都存在分量，此時稱非線性時變系統Y=f（U，t）為輸入多尺度系統；

當0＜∑bij＜∞時，說明系統的輸出在每一個尺度上都存在分量，此時稱非線性時變系統Y=f（U，t）為輸出多尺度系統；

當條件1與條件2同時滿足時，稱非線性時變系統 Y=f（U，t）為輸入輸出多尺度系統。

非線性時變系統的輸入往往無法通過測量全部獲取，對形如 Y=f（V，W，t）的非線性時變系統，其中vi∈V為系統可測輸入，wi∈W為系統不可測輸入。 此時，由于無法按式（7）、（8）計算系統的多尺度相對能量矩陣A，因此無法判斷是否屬于多尺度系統。

考慮在工程實際中，通常采集到的信號是長度有限的，故在此前提下對系統進行分析時，可以認為是有限長度的變量，此時滿足：

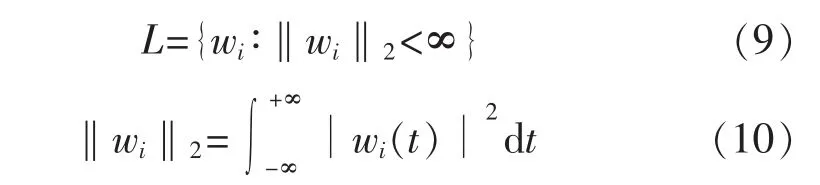
即wi可以進行快速傅里葉變換，分解為不同頻率的分量，且對某一頻率范圍 Φ∈［fjl，fjh］，通常滿足：

其中：fjl、fjh分別為對wi做k尺度小波變換后第j尺度上信號的頻率范圍。因此，對實際系統，不可測輸入wi具有多尺度特性。

將上述結論推廣至可測輸入V及輸出Y，可以看出對實際工程中出現的非線性時變系統，通常滿足輸入、輸出的多尺度相對能量強度矩陣∑aij＜∞、∑bij＜∞，即可以看作輸入輸出多尺度系統。

2 基于大數據的多尺度系統軟測量方法

論文提出的基于大數據的多尺度系統軟測量方法核心在于利用工業信息系統中的大數據，建立軟測量對象的基準模型，而后將設備運行中的可測信息與基準模型提供的參考信息進行比較構成殘差序列，并通過對殘差序列的多尺度分析構成系統的軟測量參數。

在工業生產過程中，設備并不總是固定在某個工況點運行，操作人員會根據生產需要、調度指令等對設備的工作狀態進行調整。在調整過程中，各個參數會發生不同程度的波動，即設備處于動態變化的過程中，這種工況是一種臨時的、非穩態的。

由于基準模型不但依賴于數據的真實性，而且要求各數據間具有較強的一致性，即在確定運行邊界的條件下，用于描述設備運行狀態的眾多變量符合確定的對應關系。由于工業過程通常具有大延遲、大滯后的特性，上述要求通常只有在設備長時間穩定運行時可以實現。因此，為了提高算法的精度，論文同時建立了系統的動態工況基準模型與穩態工況基準模型。

動態工況基準模型是指利用經過預處理的建模數據建立的、包含設備運行動態過程的模型。盡管動態過程中存在嚴重的不一致現象，但動態工況運行數據通常占有極大比例，將其舍棄意味著浪費了大量富含信息的數據。通過機理分析、統計分析等方法，可以改善動態工況的建模品質。

穩態工況基準模型是指利用提取了穩態工況的原始數據建立的、只包含設備穩態運行時參數對應關系的模型。

系統穩態工況的判定方法是，在時間區間［t1，t1+Δt］內，建模變量 xi滿足：

其中：xi，max、xi，min分別為 xi在時間區間［t1，t1+Δt］內的最大值和最小值；xi，e為在此工況下的額定值；δk為波動閾值；Δt及δk應根據對象的實際特性確定。

動態工況基準模型與穩態工況基準模型反映了系統不同狀態下參數間的對應關系。在建立基準模型的基礎上，將運行數據代入動態工況基準模型中，可以獲得系統動態過程的預測值為

對數據倉庫中的運行數據按式（12）提取穩態工況，將穩態工況運行數據代入穩態工況基準模型中，可以獲得系統穩態過程的預測值為

其中：yi，preDYM、yi，preSTD分別為動態模型預測值與穩態模型預測值；｛xi|xi∈［（x1，x2，…，xn）］｝為對象動態運行數據；｛xi′|xi′∈［x′1，x′2，…，x′m］｝為對象穩態運行數據。

將 yi，preDYM、yi，preSTD分別與實際運行數據比較，如式（15）、（16）所示，可以獲得系統的動態殘差 erri，DYM以及穩態殘差 erri，STD為

其中：yi、yi′分別為實際運行數據及穩態運行數據。

由于大數據的海量性，將大數據的串行處理轉變為并行處理，可以極大提高計算效率，降低計算時間。為此，論文基于信息粒化的思想，將上述動態殘差及穩態殘差進行有機結合，形成多個信息粒，而后通過對信息粒的并行計算降低狀態監測算法運行時間，節約運算資源。

由于系統總是處于穩態→動態→穩態交替運行的過程中，因此可以基于系統這種動態、穩態的交替過程劃分信息粒，即以系統的一個動態過程，或者數個連續動態過程及其相對應時間的穩態過程組成一個信息粒。

在信息粒內，穩態殘差與動態殘差屬于異步信息，二者可以看作是2種不同的傳感器對融合殘差異步觀測的結果。因此論文基于卡爾曼濾波，建立了一種簡單高效的異步信息融合算法，利用穩態殘差構建對象的差分方程，對動態殘差進行濾波，以此獲得二者的最優估計—融合殘差。算法可以通過回歸分析，利用信息粒中的穩態殘差，建立融合殘差的差分方程為

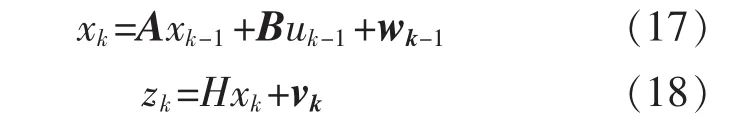
其中：wk和vk分別為過程激勵噪聲和觀測噪聲的協方差矩陣。

系統的穩態工況基準模型精確度高，且系統在穩態工況時噪聲較動態工況小，因此可以認為過程激勵噪聲的協方差矩陣wk為一個較小的常數γ。

觀測噪聲通常處于高頻段，其協方差可以由動態殘差小波變換細節重構估算出來：

其中：W（s，err）為動態殘差 errDYM在第 s尺度上小波變換的細節分量的重構。

在確定了卡爾曼濾波器的參數后，可以使用卡爾曼濾波算法，對動態殘差進行濾波，獲得二者的最優估計—融合殘差。

3 鍋爐輻射受熱面灰污的軟測量

論文研究數據來自某電廠1000 MW超超臨界機組，鍋爐為直流、單爐膛、一次再熱、切圓燃燒方式。

基準模型需要反映輻射受熱面無灰污染時，各變量的對應關系。工質吸熱動態工況基準模型為

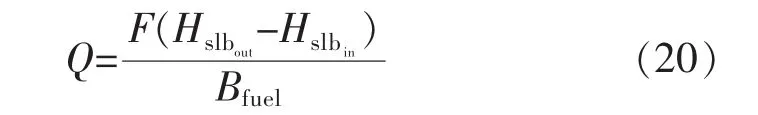
其中：Hslbout為水冷壁出口工質焓值，kJ/kg；Hslbin為水冷壁入口工質焓值，kJ/kg；F為鍋爐給水流量，t/h；Bfuel為燃料量，t/h。

基準模型表明單位燃料量釋放的熱量引起的水冷壁工質焓升。相同工況下，水冷壁無灰污染時，受熱面熱阻較小，工質可以吸收較多的熱量，而當灰渣逐漸在管壁外層積累，受熱面熱阻增加，接收相同輻射能時，工質只能吸收少部分能量，其焓升會大大降低。因此，利用工質在受到相同輻射傳熱時吸熱量的多少可以反映出受熱面灰污染程度的高低。

由于煤燃燒釋放的熱量不僅被輻射受熱面吸收，還要供應給爐膛頂部的頂棚過熱器，以及后續的二級、三級過熱器、再熱器等。因此不同受熱面吸熱量的分配會對式（20）的工質吸熱量造成影響，如表1所示。

表1 受熱面吸熱量Tab.1 Heat requirement of heat-exchanger

從表1可以看出，對中、高負荷，水冷壁吸熱量占系統總吸熱量的50%左右，波動基本不超過1%，因此，可以認為在中、高負荷下，鍋爐正常燃燒時水冷壁吸熱量占系統總吸熱量的比例基本維持不變。

論文選取了機組運行16 h的數據，此時機組運行于中、高負荷，如圖1所示。基于式（12）提取系統穩態工況，利用式（20）建立的動態工況基準模型和穩態工況基準模型的預測值與實際運行值進行比較，構成動態殘差與穩態殘差，結果如圖2所示。

圖1 機組負荷Fig.1 Unit load

圖2 穩態殘差與動態殘差Fig.2 Residuals of dynamic state and steady state

論文以每相鄰2個穩態殘差以及對應時間的動態殘差組成一個信息粒，以其中一信息粒i為例，融合殘差的差分方程為

則此信息粒的穩態殘差、動態殘差、融合殘差如圖3所示。

圖3 信息粒殘差Fig.3 Residuals of information granule

將全部信息粒進行處理，可以得到輻射受熱面吸熱量的融合殘差，如圖4所示。

從其統計數據可以看出，煤質在16 h的運行時間內不斷變化，但平均變化率較低，其波動大部分表現為一種中、高頻的小范圍抖動。因此，煤質對狀態監測結果的影響可以看做為一種中、高頻干擾，其余未建模噪聲與煤質波動具有類似的特性。通過基于小波變換的多尺度分析算法，采用haar小波基，提取其低頻分量作為鍋爐受熱面污染度指數，用以反映其灰污程度，結果如圖5所示。

圖4 融合殘差Fig.4 Fusion residuals

圖5 輻射受熱面污染度指數Fig.5 Ash pollution index of radiant heating surface

4 結語

論文提出了一種基于大數據的多尺度系統軟測量方法，利用工業信息系統中的大數據建立系統的基準模型，并將運行數據與基準模型的預測數據進行比較構成殘差序列，進而通過對殘差序列的多尺度分析構造研究對象的軟測參數，實現系統的軟測量。論文以某機組輻射受熱面灰污染程度的軟測量為例，驗證了算法的有效性。

[1]杜慶軍.電站鍋爐吹灰優化系統的研究與應用[D].北京：華北電力大學，2009.

[2]藍曉村.電站鍋爐灰污監測與吹灰優化的應用研究[D].南京：東南大學，2005.

[3]張春麗.電站鍋爐吹灰優化系統的研究與開發[D].北京：華北電力大學，2007.

[4]Piboontum S J，Swift S M，Conrad R S.Boiler modeling optimizes sootblowing[J].Power，2005，149（8）：34-37.

[5]Kalisz Sylwester，Pronobis Marek.Investigations on fouling rate in convective bundles of coal-fired boilers in relation to optimization of sootblower operation[J].Fuel，2005，84（7-8）：927-937.

[6]Erkki Valimaki，Keijo Salmenoja.Measured data for sootblowing optimization[C]//2004 TAPPI Fall Technical Conference：Engineering and Pulping，October 31，2004-November 3，2004，Atlanta，GA，United states，2004.

[7]Erkki Valimaki，Keijo Salmenoja.New tools for sootblowing optimization studies[C]//Asian Paper-New Applied Technology Conference，April27，2004-April29，2004，Suntec，Singapore，2004.

[8]Sarunac Nenad，Sale John W，Bian Xiadong，et al.Sootblowing optimization for opacity control[C]//EPA-DOE-EPRI-A and WMA PowerPlantAirPollutantControlMegaSymposium 2006，August 28，2006-August 31，2006，Baltimore，MD，United states，2006.