基于改進RBF神經網絡的鋼構件質量預測研究

雷兆明 ，王東澤 ，花季偉 ，王 軍

（1.河北工業大學 控制科學與工程學院，天津 300130；2.天津師范大學 計算機與信息工程學院，天津 300387）

近年來，隨著國民經濟的顯著提高，人們生活節奏加快，社會對橋梁、道路、商場、車站等基礎設施建設有了更高的要求，以鋼結構為主體的鋼結構建筑體系應用得到快速發展，其速度快、安全性高的特點得到了社會各界的廣泛認可[1]。質量問題是企業生產過程中最為重要的環節，因此，設計合理高效的產品質量預測系統，研究產品的質量預測問題，對于尋找生產過程中最優工藝參數，為在生產過程中實現最優控制有著重要作用。

一個完善的質量預測系統，應用生產過程中采集的大量數據進行質量預測，隨著現代化生產線快速發展，對這些數據的采集愈加完善和準確，如何高效利用這些數據，進行更加準確的質量預測，保證產品質量控制在理想的范圍內，是目前現代質量控制的重點發展方向。然而，影響產品質量的工藝參數有很多，而且他們與產品質量的關系一般存在著復雜的非線性和強耦合關系，人工神經網絡能模擬實現復雜的輸入輸出關系，適合解決非線性和不確定性高的問題。

1 改進RBF神經網絡算法

1.1 RBF神經網絡的學習

目前，徑向基函數 RBF（radial basis function）神經網絡算法在質量預測領域得到了廣泛的應用[2]，RBF神經網絡擁有強大的自學習能力，使它在應對復雜多變的生產過程中的工藝參數時，有很強的適用性；同時它的高度并行處理能力，使它在質量預測系統中，擁有很高的信息處理速度[3]。但是隨著廣大科研人員對RBF神經網絡研究的愈加深入和在眾多系統應用中得到檢驗，一些不足之處漸漸顯露出來，容易陷入局部極小值、收斂速度較慢和隱含層節點數目難以確定。針對上述缺點，采用相應的方式對其進行改進，使其在實際應用中達到更為理想的效果。

RBF神經網絡學習參數有3個：基函數中心、寬度（方差）和輸出權值。其中基函數中心和寬度直接影響輸入層到隱含層之間的空間映射結構，所以他們的選擇是重中之重。

一般可以通過3種方法來確定基函數中心，直接法、自組織學習法和有監督學習法[4]。直接法就是根據經驗和樣本特點直接確定；自組織學習法就是采用聚類方法，通常利用K-均值聚類把樣本聚成M類，這樣RBF的中心就選取類的中心；有監督學習法是讓3個參數通過監督學習后再確定，通過修正誤差一點點來優化參數。

然后，通常會用固定法來確定基函數的寬度，例如，當RBF神經網絡基函數采用高斯函數時，其方差為

式中：dmax為基函數各中心之間的最大距離；Nh為隱含層單元數量。

固定了基函數中心和寬度之后，輸入層到隱含層的空間結構就固定了，這時可以把網絡等效成一個單層網絡，并且是帶有線性輸出的，通常采用最小二乘法求權值。

1.2 遺傳算法的研究

遺傳算法是一種智能搜索算法，是在上世紀七十年代被美國學者John Holland提出的[5]，如圖1所示為遺傳算法的工作流程圖，通過觀察，可以發現遺傳算法就是通過迭代運行進行求解，具體運算流程如下：

①把要解決的問題參數集映射到合適的染色體編碼空間；

②設定適應度函數；

③設計選擇、交叉、變異等算子，然后再確定種群規模N、交叉概率和變異概率的遺傳算法參數；

④假設t=0，任意的生成N個初始個體得到種群 P（0）；

⑤評價P（t）中各個個體的適配值；

⑥判斷新種群能否終止算法，如果不能就繼續執行算法，能的話就直接輸出適配值最高的個體；

⑦得到新一代種群P（t+1），即把之前設計的選擇、交叉和變異算子作用于種群；

⑧用產生的新種群 P（t+1）代替原來的 P（t），再返回⑤繼續執行。

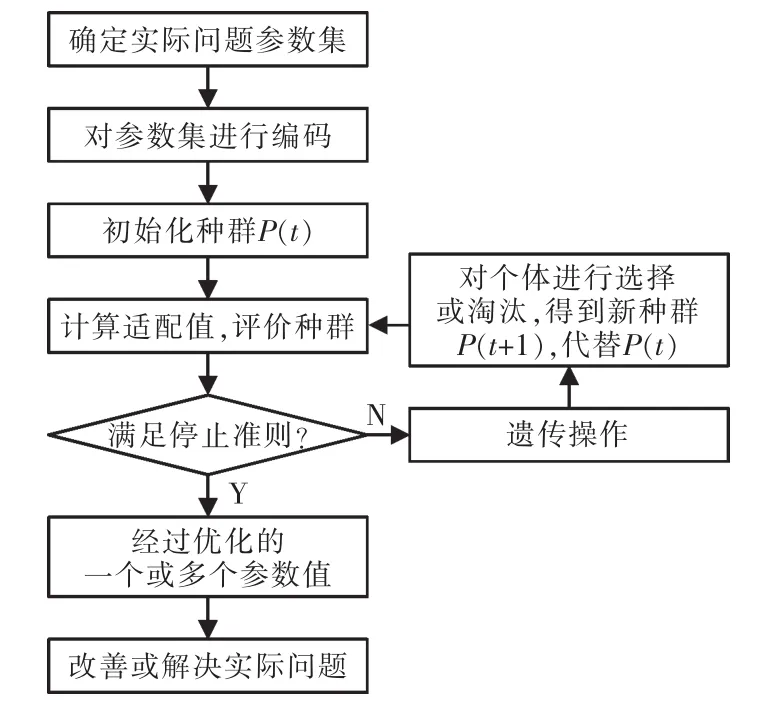
圖1 遺傳算法工作流程示意Fig.1 Genetic algorithm work flow chart

1.3 遺傳算法改進RBF神經網絡算法

由于遺傳算法具有搜索全局最優解的能力，而上面提到基函數中心和寬度對RBF神經網絡很重要，利用遺傳算法來優化RBF神經網絡的參數，可以避免局部最優的情況，所以采用遺傳算法來優化RBF神經網絡隱含層的基函數中心cj、寬度σj和權值 ωi[6]。

根據上文提到的遺傳算法尋優過程，具體操作如下：

1）編碼操作

在編碼時，把基函數中心cj、寬度σj和權值ωi放在同一條染色體上，使σj和cj交替排列，權值ωi的編碼放在染色體末端。設輸入節點數為m、隱含節點數為p、輸出節點數為n，染色體長度為l，則

染色體的結構如圖2所示。

圖2 染色體編碼示意Fig.2 Chromosome coding schemes graph

2）適應度函數的構造

遺傳算法中適應度函數是對個體評價的主要指標，進行優化時，將目標函數轉化為適應度函數，讓目標函數和適應度函數有著一致的優化方向，這樣適應度最大時目標函數也會達到最大。訓練RBF神經網絡時，希望輸出與參考輸出之間誤差盡量小，將第i個個體適應度函數表示如下：

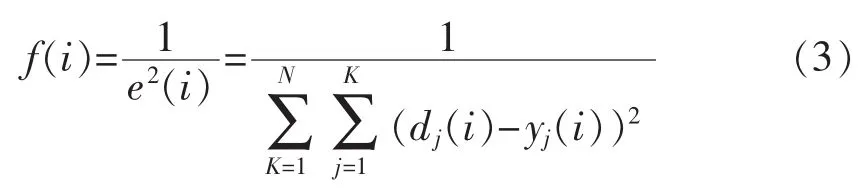
式中：dj（·）表示第 j個輸出節點的參考輸出；yj（·）表示第j個節點的實際輸出；N為訓練的樣本數量；K為輸出節點數。

3）種群初始化

本文對RBF神經網絡的基函數中心cj、寬度σj和權值ωi進行初始化。在遺傳過程中，一般的操作都是對初始種群的基因進行的，通常基因范圍不會超出原始基因，所以在遺傳算法尋優時種群初始化非常重要。

根據經驗，選取60作為種群數量，基因的初始化一般采用隨機數生成，讓基函數中心cj和寬度 σj在［-15，15］區間生成，權重 ωi在［-1，1］區間生成。

4）選擇操作

作為種群進化的核心，它決定父代種群中的個體能否遺傳到下一代中，本文選擇遺傳算法里面常用的適應度比例方法。

設個體數為N，其中個體xi的適應度為fi，pi為個體被選擇的概率，則有

選擇時，在區間［0，1］選一個隨機數 r，當 r滿足下式時，則第j個個體被選擇。

5）交叉

交叉操作分為單點和多點，單點交叉操作如圖3所示。

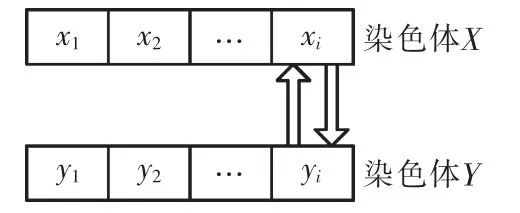
圖3 交叉操作示意圖Fig.3 Crossover operation schematic

式中，0＜α＜1，一般情況下α取隨機數或交叉概率。

6）變異

在以實數編碼的染色體中，通過變異可以得到定義空間的任何值，由于生物的基因變異具有方向不確定的特點，在應用時，采用隨機數來處理。變異時，先隨機選擇一條染色體 X=｛x1，x2，x3，…，xk，…，xn｝，再利用隨機數選擇變異基因xk，設基因xk的定義域是［xkmin，xkmax］。 然后在（0，1）區間內生成一個隨機數β，則變異后的基因xk′如下式，最后用新基因xk′替換基因xk，從而形成新的染色體。

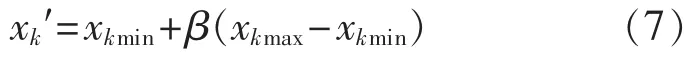
進行交叉時，先生成一個隨機數，在隨機數所對應染色體位置進行交叉變異。由于采用了實數編碼，因此定義交叉后基因式如下：

2 質量預測的仿真與結果分析

2.1 仿真中輸入輸出的選擇

在大型鋼構件加工生產過程中，焊接是影響產品質量最為重要的工序，焊接質量更會直接影響整個構件甚至整個工程的質量。本文以河北某個大型鋼構件制造業為背景，以質量問題和焊接過程中的工藝參數作為RBF神經網絡的輸入，造成質量問題的原因作為輸出，質量問題包括咬邊、飛濺、夾渣、弧坑裂紋、接頭不良、氣孔6個主要問題，工藝參數包括電流、電壓、CO2流量、焊接速度、裝配間隙、焊條直徑和焊件厚度，輸出為造成質量問題原因編碼。質量問題的編碼如表1所示，輸入對應如表2所示，輸出位對應編碼如表3所示。

表1 質量問題編碼表Tab.1 Quality problem code table

表2 輸入變量對應表Tab.2 Table of input variables

表3 輸出位對應編碼表Tab.3 Coding schedule of output bit

2.2 仿真結果與分析

本文中選取30組從實際生產中采集的數據進行仿真，如表4所示，仿真過程中隱含層節點數為20，訓練誤差精度為10-2。

表4 樣本數據Tab.4 Table of sample data

采用RBF神經網絡進行仿真，得到的仿真結果如圖4所示，從結果中可以看出，訓練沒有達到要求的精度，訓練200次以后，系統誤差不再減少，即陷入局部最優，因此需要改進RBF神經網絡算法。

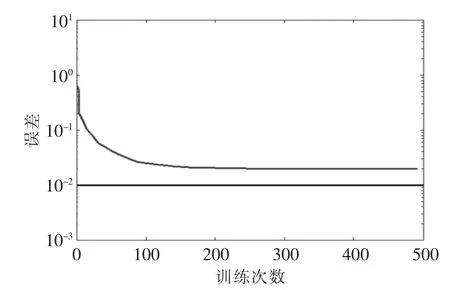
圖4 樣本訓練誤差與進化次數仿真結果（RBF）Fig.4 Samples training error and the number of evolution simulation result

用遺傳算法改進RBF神經網絡之后，得到如圖5所示的仿真結果，從中發現誤差隨著訓練次數快速下降，能夠達到10-2以下。

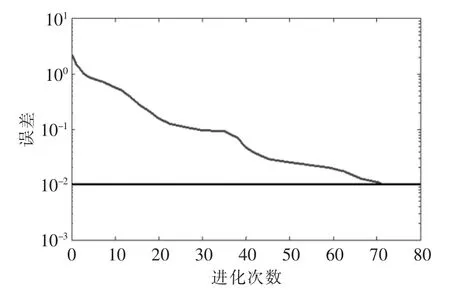
圖5 樣本訓練誤差與進化次數仿真結果（改進RBF）Fig.5 Samples training error and the number of evolution simulation result

用樣本｛5，420，36，18，1.2，1，1.6，6｝對訓練后的RBF進行驗證，系統輸出為｛0.0023，-0.0016，-0.0011，1.0027，0.0039｝，經過取整后為｛0，0，0，1，0｝，轉化為質量問題原因后是焊接速度過大，診斷結果符合實際情況。以此方法一共用5組樣本對訓練后的RBF神經網絡進行驗證，得到驗證結果均與實際結果相符，驗證結果如表5所示。

表5 樣本驗證結果Tab.5 Table of sample test results

3 結語

針對大型鋼構件生產過程中的質量問題，本文采用改進RBF神經網絡進行預測，RBF神經網絡本身具有強大的學習能力和適用性，采用遺傳算法對其進行改進，優化了RBF神經網絡主要參數的選擇，相比較于其他算法，遺傳算法更可避免其陷入局部最優。最后，通過仿真證明，該方法應用在實際質量預測中是有效的，在實際生產中可得到推廣。

[1]賀海勃.淺議鋼構件加工質量控制[J].中國建筑金屬結構，2013（8）：77-79.

[2]雷琪，劉君賢，何勇，等.基于PCA與RBF的焦炭質量預測模型[J].控制工程，2010，17（4）：513-516，520.

[3]Han H G，Chen Q，Qiao J F.An efficient self-organizing RBF neural network for water quality prediction[J].Neural Networks，2011，24（7）：717-725.

[4]Schubert M，Muffler A，Mourad S.The use of a radial basis neural network and genetic algorithm for improving the efficiency of laccase-mediated dye decolourization[J].Journal of Biotechnology，2012，161（4）：429-436.

[5]辛若波.基于遺傳優化和貝葉斯正規化神經網絡的空氣質量預測研究[D].山東：山東大學，2013.

[6]李寶棟，宿忠娥，吳曉紅，等.基于GA-RBF神經網絡的電火花成形加工電參數優化[J].工業儀表與自動化裝置，2013（2）：87-89.