PSO動態(tài)優(yōu)化的ADRC控制器研究

張墩利 ，周國棟 ，2，張 健

（1.湖南廣播電視大學 機電工程系，長沙410004；2.中南大學 機電工程學院，長沙 410083；3.國網(wǎng)天津城東供電公司，天津 300000）

目前，自抗擾控制器（ADRC）的參數(shù)都是線下靜態(tài)優(yōu)化，好處是計算速度快，并且能解決大部分工業(yè)系統(tǒng)帶來的干擾[1-2]，但是在大時滯和強干擾系統(tǒng)中，如熱工系統(tǒng)，靜態(tài)的參數(shù)往往會帶來輸出超調(diào)甚至不穩(wěn)定[3]。這時靜態(tài)參數(shù)機制的ADRC暴露出其局限性。

針對以上問題，本文提出動態(tài)優(yōu)化ADRC算法。該算法的核心思想是根據(jù)擾動量，動態(tài)調(diào)整擴張狀態(tài)觀測器（ESO）的誤差估計系數(shù)。

粒子群優(yōu)化算法（PSO）在多目標參數(shù)優(yōu)化中具有收斂速度快、計算效率高等特點，將用于ESO誤差系統(tǒng)的動態(tài)調(diào)整。

1 典型ADRC控制器及其改進研究

ADRC是一種新型非線性PID控制器。該控制器不需要被控對象的精確數(shù)學模型便可以實現(xiàn)高精度控制，具有響應速度快、抗干擾能力強、魯棒性強等優(yōu)點[4]，因此具有很強的工業(yè)實用價值。在電力系統(tǒng)、機器人控制、電機控制、飛行控制等領(lǐng)域得到廣泛應用[5]。

典型的二階ADRC結(jié)構(gòu)如圖1所示，主要由3部分組成，分別是輸入跟蹤微分器（TD）、擴張狀態(tài)觀測器（ESO）和非線性反饋控制器（NLSEF）。

圖1 ADRC控制器結(jié)構(gòu)圖Fig.1 Diagram of ADRC regulator

其中，TD的作用是為輸入控制信號安排過渡過程并提取微分信號，其計算表達式為

式中：h0為濾波因子；r為跟蹤速度參數(shù)。

ESO是ADRC控制器的核心部件，其作用是估算出系統(tǒng)的內(nèi)外擾動總和，表達式為

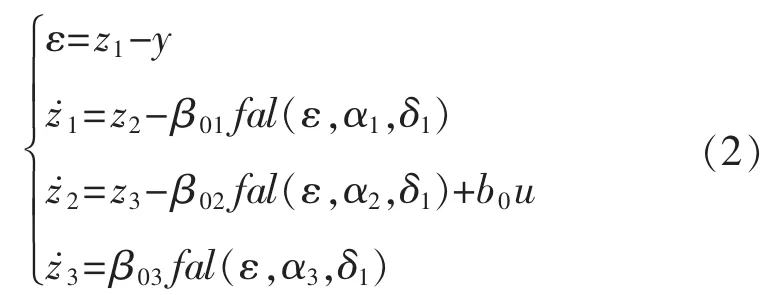
ESO估算的擾動量是否準確，決定于3個關(guān)鍵參數(shù) β01，β02和 β03。

NLSEF主要是根據(jù)輸入微分信號和ESO的狀態(tài)變量反饋值計算出輸出控制量，該計算律實際上是非線性PD控制算法。其表達式為

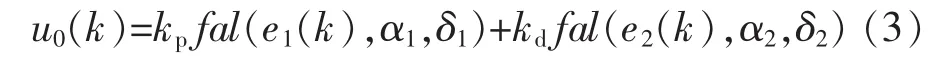
式中， fst（）函數(shù)和 fal（）函數(shù)參見文獻[4]。

由于ADRC控制器參數(shù)多，調(diào)節(jié)十分困難。近年來，對ADRC控制器優(yōu)化、改造的研究很多，出現(xiàn)了模糊ADRC[6]、混沌粒子群優(yōu)化ADRC[7]、免疫微粒群自抗擾控制[8]等。這些智能算法的引入大大提高了該控制器參數(shù)整定效率，擴展了其實用價值。但這些改進大都是采用靜態(tài)優(yōu)化機制，因此ESO的誤差估計范圍往往有限，一旦系統(tǒng)時滯嚴重或干擾跳動大，實際誤差超出設(shè)計范圍，系統(tǒng)將出現(xiàn)紊亂。這正是靜態(tài)估算機制暴露出的不足。

2 PSO動態(tài)優(yōu)化ADRC設(shè)計

2.1 PSO-ADRC結(jié)構(gòu)

粒子群優(yōu)化算法（PSO）是進化算法的一種[9-10]，該算法的求解過程是從一組隨機初始解出發(fā)，通過鄰域搜索計算方法，不斷迭代尋優(yōu)，在每次迭代計算中，粒子群通過個體最優(yōu)解和群體最優(yōu)解不斷更新自己，直至找到最優(yōu)解。相比遺傳算法等進化算法，粒子群算法沒有交叉和變異運算，可采用實數(shù)編碼，結(jié)構(gòu)簡單，計算速度快，作為在線優(yōu)化的算法具有很大優(yōu)勢[11]。

采用PSO動態(tài)優(yōu)化的ADRC結(jié)構(gòu)如圖2所示。PSO嵌入在ESO前，其作用是優(yōu)化ESO的3個擾動量估計系數(shù)。

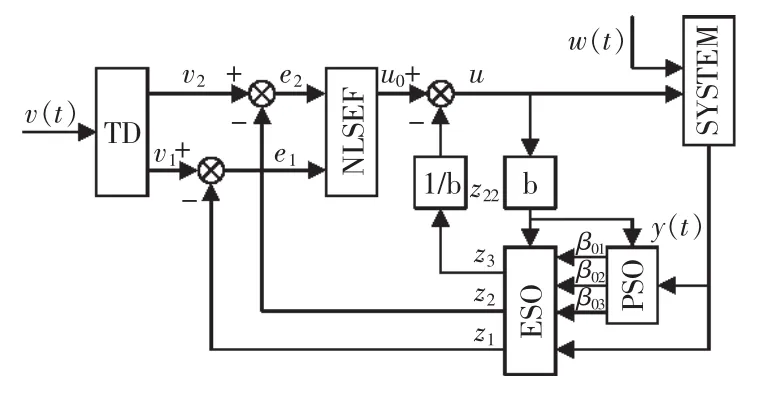
圖2 PSO-ADRC控制器結(jié)構(gòu)圖Fig.2 Structure of PSO-ADRC

動態(tài)優(yōu)化面臨的主要問題是實時性如何保證。為獲取最大的計算效率，做了2個方面的改進：因為ADRC自身有抗干擾能力，因此沒有必要每次都需要PSO在線優(yōu)化，只有滿足一定條件下才有必要進行優(yōu)化，本實驗中設(shè)置了一個誤差閾值，只有當誤差大于設(shè)定的閾值，PSO的在線優(yōu)化才會啟動；其次是PSO算法的時間復雜度本來就高，為滿足控制系統(tǒng)的實時性要求，有必要對現(xiàn)有PSO算法進行改進。

2.2 Pareto精英保留策略PSO

為提高計算效率，在經(jīng)典PSO算法基礎(chǔ)上采用了Pareto精英保留策略[12]，該算法也稱非劣最優(yōu)求解，其運算流程如圖3所示。

圖3 PSO優(yōu)化流程Fig.3 Optimize process of PSO

Pareto-PSO方法是使用優(yōu)化前的ESO誤差系數(shù)作為初始值，不斷保留進化過程中的精英。為克服粒子群算法的早熟缺陷，對適應度函數(shù)加以改進，加入粒子的密集度和優(yōu)勢度參數(shù)，其計算律為

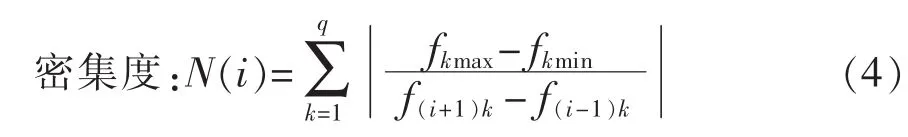
式中：q為待優(yōu)化函數(shù)的維度；fkmax和 fkmin函數(shù)為第k 個待優(yōu)化函數(shù)的 2 個極值；f（i+1）k和 f（i-1）k為粒子的相鄰粒子的第k個待優(yōu)化函數(shù)值。

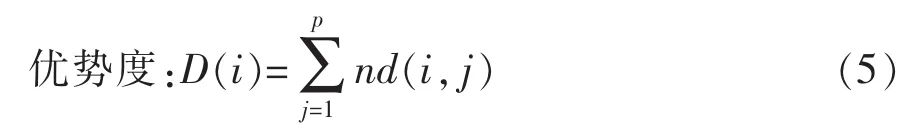
式中：p 為鄰域范圍；nd（i， j）為粒子優(yōu)勢計算值，當i粒子優(yōu)于j粒子時值為1，反之為0。

粒子群適應度函數(shù)計算律為

式中：ess、e（t）、Mp分別為穩(wěn)態(tài)誤差、反饋誤差和超調(diào)量；Kess、Ke、Kmp為相應系數(shù)。 優(yōu)化目標為使 J值取值最小。

3 仿真研究

仿真環(huán)境：計算機處理器為英特爾CORE i5 2.5 GHz，內(nèi)存 4 GB，WINDOWS7 操作系統(tǒng)，采用MATLAB 9.0編寫算法程序。

實驗分別采用ADRC控制算法和本文提出的PSO-ADRC控制算法對典型時滯系統(tǒng)進行在線優(yōu)化，以文獻[3]中的熱工時滯系統(tǒng)為例，其傳遞函數(shù)為

式中，kp、Tp、τ為隨鍋爐運行工況不同而變化的參數(shù)。本實驗采用65%負荷狀態(tài)，其參數(shù)kp=7.5，Tp=150，τ=45，α=12。

ADRC控制器參數(shù)值設(shè)置如表1所示。

表1 ADRC系統(tǒng)參數(shù)Tab.1 Parameters of ADRC

3.1 魯棒性能測試

當系統(tǒng)負荷從65%跳變到100%時，以上參數(shù)也隨之會產(chǎn)生攝動，系統(tǒng)分別采用ADRC控制器和PSO-ADRC（粒子群優(yōu)化自抗擾控制）控制器，其中PSO-ADRC控制器參數(shù)初始種群數(shù)為200，尋優(yōu)最大迭代次數(shù)為tmax=1000，PSO優(yōu)化啟動誤差閾值為4%，其階躍響應曲線分別如圖4所示，從圖中可以看出，ADRC控制器的輸出超調(diào)量為 20%，PSOADRC控制器的輸出超調(diào)量為14.7%，但系統(tǒng)調(diào)節(jié)時間比ADRC延長了64 s。

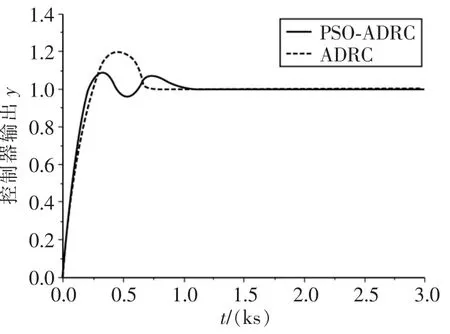
圖4 PSO-ADRC魯棒性仿真測試Fig.4 Robustness simulation tests of PSO-ADRC

3.2 抗干擾仿真測試

在輸入信號中加入一段大的擾動信號，其響應曲線如圖5所示，從圖中可以看出，超調(diào)量從18%減少到3%，但調(diào)節(jié)時間延長了32 s。

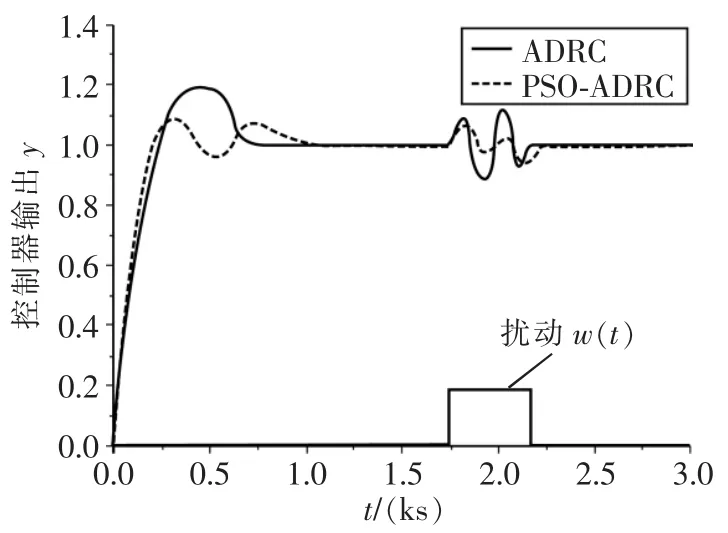
圖5 PSO-ADRC抗干擾仿真測試Fig.5 Anti-interference simulation test of PSO-ADRC

4 結(jié)語

本文根據(jù)ADRC控制器的特點，針對其在大時滯系統(tǒng)和強干擾系統(tǒng)控制中的不足，以動態(tài)調(diào)整其誤差估計系數(shù)的實時優(yōu)化為方案，采用改進的Pareto精英保留PSO算法進行實時快速優(yōu)化。針對熱工時滯系統(tǒng)的仿真實驗結(jié)果表明，對于大時滯和強干擾系統(tǒng)的控制具有很好的性能改善。

[1]潘文婷，孫運全，盛吉.基于粒子群的自抗擾靜止同步補償器仿真研究[J].計算機仿真，2011，28（8）：298-301.

[2]楊瑞光，孫明瑋，陳增強.飛行器自抗擾姿態(tài)控制優(yōu)化與仿真研究[J].系統(tǒng)仿真學報，2010，22（11）：2689-2693.

[3]管志敏.自抗擾控制器對一類熱工對象的控制性能研究[J].熱能動力工程，2011，26（4）：445-448.

[4]韓京清.自抗擾控制技術(shù)-估計補償不確定因素的控制技術(shù)[M].北京：國防工業(yè)出版社，2008.

[5]劉昊，王濤，范偉，等.氣動人工肌肉關(guān)節(jié)的自抗擾控制[J].機器人，2011，33（4）：461-466.

[6]宗陽，張科，王靖宇.一種基于模糊ADRC的舵機控制算法設(shè)計與實現(xiàn)[J].西北工業(yè)大學學報，2011，29（2）：217-221.

[7]程啟明，程尹曼，汪明媚，等.基于混沌粒子群算法優(yōu)化的自抗擾控制在蒸汽發(fā)生器水位控制中的應用研究[J].華東電力，2011，39（6）：311-314.

[8]劉朝華，張英杰，章兢，等.基于免疫雙態(tài)微粒群的混沌系統(tǒng)自抗擾控制[J].物理學報，2011，60（1）：69-74.

[9]J Kennedy，R Eberbarl.Particle swarm optimization[C]//Proc IEEE Int Conf on Nerural Networks，Perth，1995：1942-1948.

[10]R Eberbarl，J Kennedy.A new optimizer using particle swarm theory[C]//Proc 6th Int Symposium on Micro.Machine and Human Science，Nagoya，1995：39-43.

[11]張海軍，岳恒，李春，等.基于PSO在線優(yōu)化的多模型自適應動態(tài)矩陣控制[J].系統(tǒng)仿真學報，2007，19（15）：3506-3509.

[12]陳錦珠，郭文忠，陳國龍.求解VLSI布圖規(guī)劃問題的多目標粒子群優(yōu)化算法[J].計算機工程與科學，2010，32（9）：57-60.