七模類Lorenz系統的界估計及計算機仿真

徐鴻鵬，王記昌

（河南工業職業技術學院 河南 南陽 473000）

1963年美國科學院院士E.N.Lorenz在研究大氣對流時，首次給出了一個簡單的三維自治系統，即著名的Lorenz系統[1]，采用的辦法就是對Navier-Stokes方程和熱傳導方程進行Fourier級數展開進行截取前三項所得。以后，又有其他學者進行有限項截斷，得到不同模數的非線性微分方程組[2-4]。混沌吸引子是相空間中的一個點集，隨著運動時間的增加，所有軌線都趨向于它。這些混沌系統的全局吸引子的存在性和部分動力學行為已經被許多研究者所認識和研究。除了Lorenz系統族[5]之外，也存在其他混沌系統[6]，這些新混沌系統的提出和研究為混沌系統甚至混沌理論的應用提供了一定的理論基礎和參考價值。文獻[7]研究了Navier-Stokes方程的七模截斷的全局吸引子的存在性，并給出了部分數值模擬圖像，本文進一步考慮該系統，通過理論和數值方法給出了系統的相圖、Poincare映射圖、分岔圖等揭示系統的復雜動力學行為，并構造出廣義李雅普諾夫函數給出了新的全局指數吸引集的估計表達式，并給出理論計算和實際數值計算的結果比較，表明了本文方法的正確性。

1 數學模型及其主要結果

王賀元等研究的一個七模Lorenz混沌系統的方程為[7]:

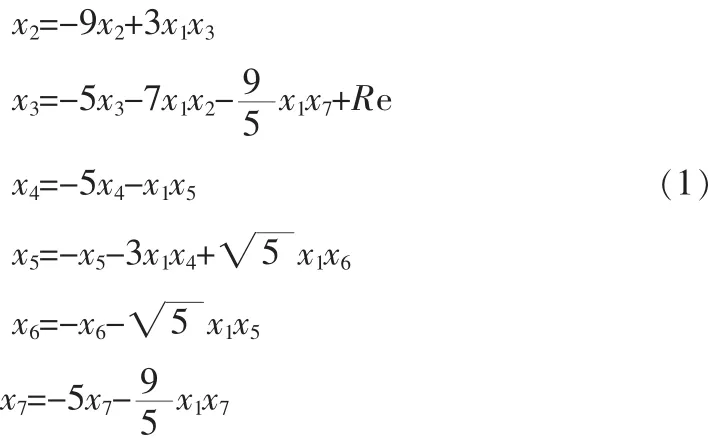
其中（x1，x2，x3，x4，x5，x6，x7）∈R7為狀態變量，R e 為系統實參數。

系統（1）在坐標變換下（x1，x2，x3，-x4，-x5，-x6，x7）保持不變，說明系統具有該變化下的對稱性。根據劉維爾定理，由于系統的平均散度所以系統屬于耗散系統，并以指數e-28t收縮，說明系統存在吸引子。當R e=100時，初值取（1，1，1，1，1，1，1），系統（1）的軌線的吸引子相圖如圖1所示。

隨著參數R e的變化，系統表現出穩定到平衡點、極限環 （周期軌或擬周期軌）和混沌吸引子等不同的非線性行為，即出現Hopf分叉和混沌現象。下面通過數值模擬給出不同于典型混沌吸引子的復雜周期軌的吸引子相圖以驗證圖4中的結論，此時R e=200。并結合Poincare映射圖來進一步加以說明，Poincare映射截面上有一些具有分形結構的密集點，說明系統是混沌狀態，截面上只有幾個離散的點，說明系統處于周期狀態或擬周期狀態。這與圖3和圖5的結論是吻合的。

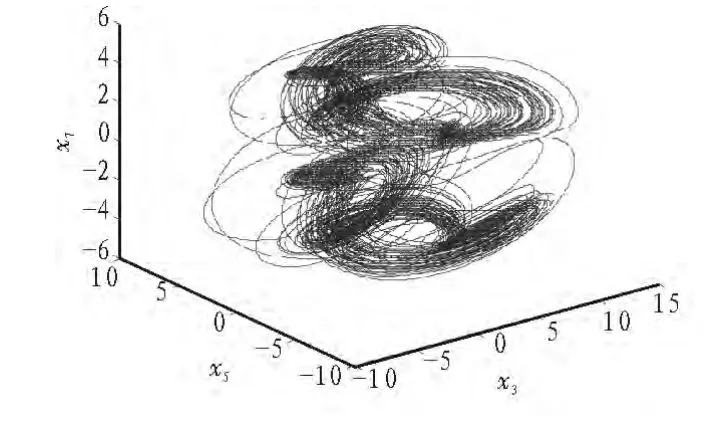
圖1 系統（1）的軌線相圖Fig.1 Phase portrait of system （1）

圖2 系統（1）的分岔圖Fig.2 Bifurcation diagram of system （1）

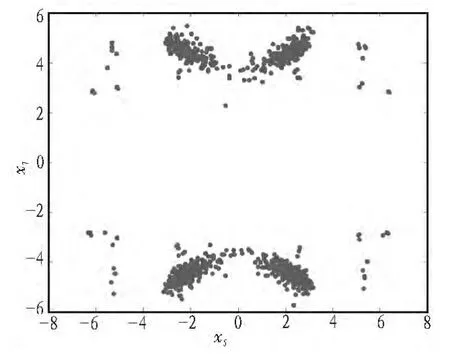
圖3 Poincare映射圖Fig.3 Poincare mapping diagram

圖4 系統（1）的復雜周期軌Fig.4 Complex periodic orbit of system （1）

2 系統的界估計和數值模擬

下面給出系統的界估計和最終有界集的結論。

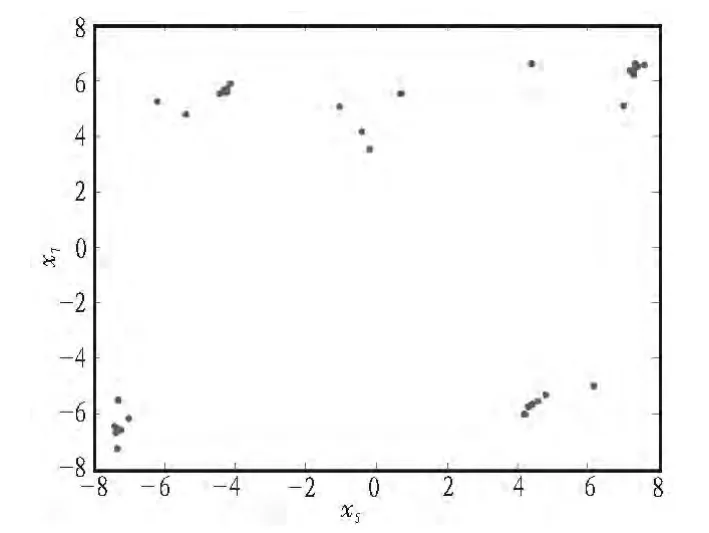
圖5 系統（1）的Poincare映射圖Fig.5 Poincare mapping diagram of system （1）

對V沿系統（1）的軌線對時間求導有，

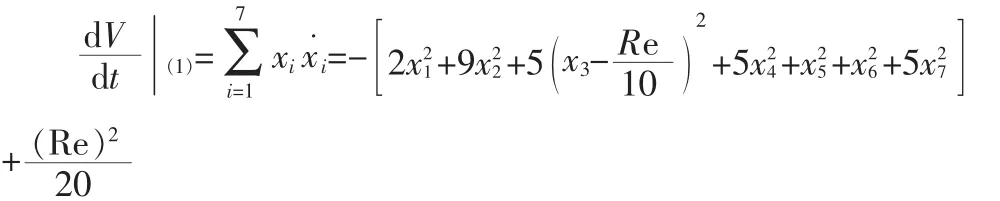
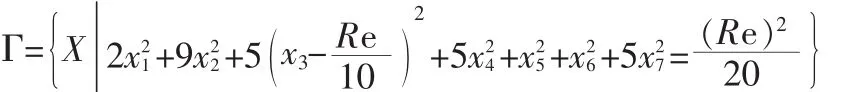
注1：本文給出的結論比文獻[7]的范圍更小，為了便于比較，采用文獻[7]的符號記法，在文獻[7]中的結論

注2：該定理不僅給出了系統解的最終界估計式，而且給出了系統（1）的軌線從吸引集外進入吸引集的速率估計表達式。

當參數R e=100時，系統（1）的最終界估計表達式為，Ω=數值模擬如圖15所示。

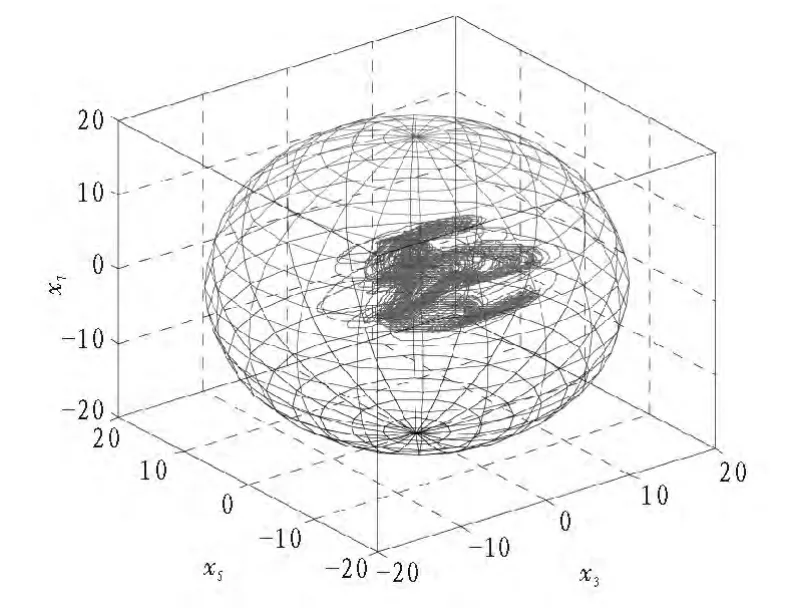
圖6 混沌吸引子的最終界Fig.6 Ultimate bound of chaotic attractor

3 結 論

本文研究了參數Re變化時系統（1）的部分動力學行為和全局指數吸引集，并且給出了相應的計算機仿真[9]。由于該系統具有豐富的動力學行為，可以為信息加密技術提供良好的信號源，因此其混沌機理的研究以及電子振蕩電路的實現是我們下一步研究的重點任務。

[1]Lorenz E N.Deterministic non-periods ows[J].J.Atoms.Sci.1963，20（2）:130-141.

[2]Franceschini V，Tebaldi C.A seven-modes truncation of the plane incompressible Navier-Stokes equations[J].Journal of Statistical Physics，1981，25（3）:397-417.

[3]Boldrighini C，Franceschini V.A five-dimensional truncation of the plane incompressible Navier-Stokes equations[J].Communications in Mathematical Physics，1979，64（2）:159-170.

[4]Franceschini V，Zanasi R.Three-dimensional Navier-Stokes equations truncated on a torus[J].Nonlinearity，1992，4（3）:189-209.

[5]尹社會，張勇，張付臣，等.基于Lorenz系統的強迫Lorenz混沌系統的動力學研究[J].東北師大學報（自然科學版），2014，46（1）:42-47.YIN She-hui，ZHANG Yong，ZHANG Fu-chen，et al.Dynamical behavior for the forced Lorenz system based on the Lorenz map and simulation[J].Journal of Northeast Normal University（Natural Science Edition），2014，46（1）:42-47.

[6]尹社會，張勇，徐鵬飛.一個三維混沌系統的動力學行為及反饋同步[J].江西科學，2013，31（6）:717-721.YIN She-hui，ZHANG Yong，XU Peng-fei.Dynamical analysis and feedback synchronization of a Three-dimensional Chaotic System[J].Jiangxi Science，2013，31（6）:717-721.

[7]WANG He-yuan，CUI Yan，HUANG Min.A new sevenmodes truncation of the plane incompressible Navier-Stokes equations[J].Chinese Quarterly Journal of Mathematics，2012，27（1）:11-17.

[8]Damei Li，Jun-an Lu，Xiaoqun Wu，et al.Estimating the bounds for the Lorenz family of chaotic systems[J].Chaos，Solutiona and Fractals，2005，23（2）:529-534.

[9]尤裕榮，袁洪濱，王春民，等.PWM高速開關閥動態調節特性仿真研究[J].火箭推進，2012（5）：24-29.YOU Yu-rong，YUAN Hong-bin，WANG Chun-min，et al.Simulation of dynamic regulating characteristics of PWM high-speed on-off valve[J].Journal of Rocket Propulsion，2012（5）:24-29.