基于掩碼的AES算法抗二階DPA攻擊方法研究

呂 慧，趙躍華

（江蘇大學(xué) 計(jì)算機(jī)科學(xué)與通信工程學(xué)院，江蘇 鎮(zhèn)江 212013）

隨著科技的不斷進(jìn)步，內(nèi)嵌密碼模塊的智能設(shè)備和嵌入式設(shè)備已廣泛應(yīng)用于各類信息產(chǎn)品與通信系統(tǒng)中。密碼芯片的安全問(wèn)題也成為了當(dāng)今社會(huì)人們非常關(guān)注的問(wèn)題。在紛繁復(fù)雜的各類攻擊方式中，側(cè)信道攻擊是最有效的攻擊方式之一，對(duì)諸如智能卡這樣的智能設(shè)備的實(shí)際安全性造成了極大的威脅。

AES算法作為新一代高級(jí)加密標(biāo)準(zhǔn)，是一種迭代型分組密碼算法，在各類信息產(chǎn)品中應(yīng)用十分廣泛。本文主要研究基于AES加密的密碼芯片能量分析攻擊技術(shù)與防御技術(shù)。

掩碼方法是目前使用最廣泛的抗能量分析攻擊方法，國(guó)內(nèi)外專家學(xué)者對(duì)掩碼方法進(jìn)行了深入的研究，首先提出的是隨機(jī)掩碼的概念，之后提出了固定值掩碼方案。隨著加密和破譯技術(shù)的不斷進(jìn)步，在抗一階能量分析攻擊的防御技術(shù)趨于成熟時(shí)，學(xué)者們又把目光投向了高階能量分析攻擊的防御方法上。文獻(xiàn)[1-3]對(duì)抗高階能量分析攻擊方法進(jìn)行了深入研究，Rivain等[1]研究了高階掩碼型S盒的設(shè)計(jì)過(guò)程，文獻(xiàn)[2]利用仿射掩碼來(lái)實(shí)現(xiàn)抗高階能量分析，文獻(xiàn)[3]則是采用加法掩碼和乘法掩碼相結(jié)合的方法。考慮到現(xiàn)實(shí)應(yīng)用的可能性，本文以資源受限的智能卡設(shè)備為研究對(duì)象，在現(xiàn)有掩碼算法分析研究的基礎(chǔ)上，提出了一種改進(jìn)的掩碼防御算法。該算法綜合考慮了實(shí)現(xiàn)的安全性和資源開(kāi)銷，且能夠抵抗一階和二階差分能量分析攻擊，是一種安全性高、易于實(shí)現(xiàn)的掩碼防御算法。

1 AES算法描述

AES算法是NIST于2000年宣布用于替代DES的分組密碼標(biāo)準(zhǔn)，也是目前最完善的密碼體系，因此針對(duì)AES的能量分析攻擊及其防御措施成為研究的熱點(diǎn)。AES算法是一種靈活的算法，密鑰長(zhǎng)度一般有128bit、192bit和256 bit 3種，本文以128 bit為例來(lái)說(shuō)明。AES將每一個(gè)分組，128 bit的輸入和128 bit的密鑰都作為一個(gè)以字節(jié)為單位的4×4矩陣（State），AES是迭代型密碼，128 bit密鑰的情況共有10輪運(yùn)算。核心算法就是輪函數(shù)對(duì)State的重復(fù)作用。輪函數(shù)由4個(gè)可逆的內(nèi)部函數(shù)構(gòu)成，包括：輪密鑰加（AddRoundKey）、字節(jié)代換（SubBytes）、行移位（ShiftRows）和列混淆（MixColumns）。

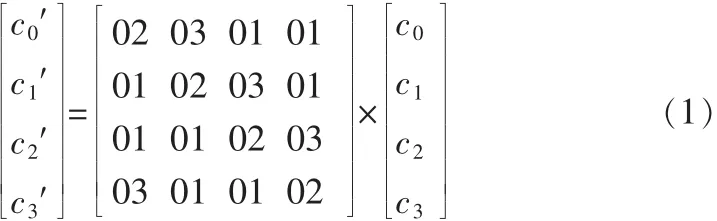
在AES算法的4個(gè)內(nèi)部函數(shù)中，SubBytes是AES算法中唯一的非線性變換，往往通過(guò)查表來(lái)實(shí)現(xiàn)。MixColumns操作把狀態(tài)的每一列看作GF（28）域上的多項(xiàng)式，并與一個(gè)固定的多項(xiàng)式 C（x）={03}x3+{01}x2+{01}x+{02}相乘，然后模多項(xiàng)式x4+1取余，列混淆運(yùn)算過(guò)程如式1所示。

輸入的128 bit的密鑰經(jīng)過(guò)密鑰擴(kuò)展函數(shù)KeyExpansion之后擴(kuò)展成11個(gè)密鑰塊，提供給輪函數(shù)作輪密鑰加運(yùn)算。除了第一輪運(yùn)算之前有一個(gè)AddRoundKey，和最后一輪運(yùn)算省略MixColumns操作之外，其余9輪運(yùn)算的輪函數(shù)完全相同。AES算法加解密過(guò)程如圖1所示。

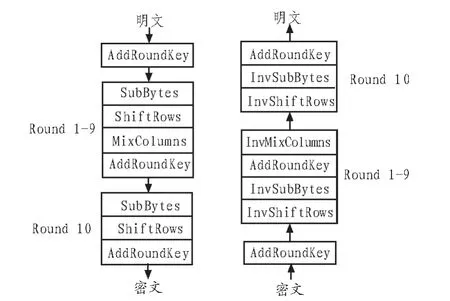
圖1 AES算法加解密流程圖Fig.1 The flow chart of AESencryption and decryption algorithm

2 能量分析攻擊與防御技術(shù)

2.1 能量分析攻擊與防御概述

智能卡現(xiàn)在已經(jīng)廣泛應(yīng)用于各類密碼設(shè)備中，用以提供強(qiáng)有力的用戶認(rèn)證，并安全地儲(chǔ)存密碼信息。然而，1998年，當(dāng)Kocher等指出能量分析攻擊能夠有效地揭示出智能卡中的秘密信息時(shí)，人們對(duì)密碼設(shè)備安全性的傳統(tǒng)看法瞬間崩塌。

能量分析攻擊的基本思想是通過(guò)分析密碼設(shè)備的能量消耗獲得其密鑰，而這種攻擊主要利用了兩類能量消耗依賴性：數(shù)據(jù)依賴性和操作依賴性。常見(jiàn)的能量分析攻擊類型主要有：簡(jiǎn)單能量分析攻擊 （SPA）、差分能量分析攻擊（DPA）、高階差分能量分析攻擊（HO-DPA）以及相關(guān)性能量分析攻擊等。

能量分析攻擊能夠?qū)嵤┑囊罁?jù)是密碼設(shè)備的能量消耗依賴于設(shè)備所執(zhí)行的密碼算法的中間值，因此，要試圖抵御這種攻擊，就要降低甚至消除這種依賴性，使得密碼設(shè)備的能量消耗獨(dú)立于設(shè)備所執(zhí)行的密碼算法的中間值。目前已公開(kāi)的抗能量分析攻擊的各種對(duì)策本質(zhì)上可以分為隱藏技術(shù)和壓那么技術(shù)兩大類。

2.2 現(xiàn)有的基于AES算法的抗能量分析方法

目前，針對(duì)AES算法的抗能量分析研究已取得大量的研究成果。Messerges提出了隨機(jī)掩碼算法，在每一輪加密運(yùn)算時(shí)都產(chǎn)生一組隨機(jī)掩碼，然后分別將它們與輪密鑰和明文進(jìn)行異或運(yùn)算，將掩碼操作后的輸出進(jìn)行相應(yīng)的輪函數(shù)運(yùn)算。在該隨機(jī)掩碼機(jī)制中，每一輪的輪函數(shù)都需要生成一個(gè)新的隨機(jī)掩碼值，并需要根據(jù)這個(gè)掩碼值實(shí)時(shí)計(jì)算出其相對(duì)應(yīng)的掩碼型S盒，需要很大的軟硬件開(kāi)銷。

為了解決隨機(jī)掩碼防御機(jī)制需要很大軟硬件開(kāi)銷的難題，文獻(xiàn)[4]提出了一種新的掩碼機(jī)制，即乘法掩碼。在該防御策略中，用于對(duì)輸入信息保護(hù)的掩碼和用于對(duì)輸出信息進(jìn)行恢復(fù)的修正掩碼是相同的。因此不需要再重新計(jì)算和保存掩碼后的S盒，能有效降低掩碼防御算法的軟硬件開(kāi)銷。然而，文獻(xiàn)[5]指出，乘法掩碼并不能有效抵抗能量分析攻擊和零值攻擊。

Messerges等提出了一種簡(jiǎn)化的固定值掩碼方法[6]，該方法需要預(yù)先產(chǎn)生q組單字節(jié)掩碼值并計(jì)算相對(duì)應(yīng)的掩碼型S盒，并將掩碼值及其相對(duì)應(yīng)的S盒保存在ROM中。執(zhí)行加密算法前，密碼設(shè)備先在q組掩碼值中隨機(jī)選取一組，加密過(guò)程中，就使用該掩碼值及其對(duì)應(yīng)掩碼型S盒對(duì)明文進(jìn)行掩碼。固定值掩碼與隨機(jī)掩碼方法相比，資源占用量更少，所需存儲(chǔ)空間也更少，因而更具有現(xiàn)實(shí)意義。但文獻(xiàn)[7]指出該方法不能抗二階能量分析攻擊，無(wú)法滿足實(shí)際應(yīng)用的需求，并在此基礎(chǔ)上作出了改進(jìn)，對(duì)AES的四輪運(yùn)算分別用不同的掩碼值進(jìn)行掩碼，但是該方法仍然存在著信息泄漏的風(fēng)險(xiǎn)，在抗二階DPA和CPA攻擊上仍然存在著安全隱患。

3 一種改進(jìn)的掩碼防御方法

3.1 改進(jìn)的掩碼防御方案設(shè)計(jì)

固定值掩碼方法不能抗二階差分能量攻擊，其原因主要在于該掩碼加密算法執(zhí)行過(guò)程中，存在著一輪以上使用了同樣的掩碼值的情況，攻擊者可通過(guò)關(guān)聯(lián)進(jìn)行差分統(tǒng)計(jì)來(lái)消除這一掩碼。實(shí)驗(yàn)證明，掩碼的橫向重用和縱向重用都會(huì)使得加密算法易受二階差分能量分析攻擊和相關(guān)性能量分析攻擊。本文在簡(jiǎn)化的固定值掩碼方法的基礎(chǔ)上，為提高加密設(shè)備抗二階能量分析攻擊的能力，提出了一種改進(jìn)的掩碼防御算法。其基本設(shè)計(jì)思想如下：

1）為了解決固定值掩碼方法一輪以上使用了相同的掩碼值的問(wèn)題，本文根據(jù)高級(jí)加密標(biāo)準(zhǔn)AES算法自身的特性，對(duì)AES算法的四輪運(yùn)算，對(duì)應(yīng)四組掩碼值，預(yù)先計(jì)算并分別存放在不同的寄存器中，每輪加密運(yùn)算過(guò)程中的3步運(yùn)算（列混淆操作除外），從不同的寄存器中隨機(jī)抽取3個(gè)掩碼值分別進(jìn)行掩碼，從而降低了多輪采用同一掩碼值的可能性。

2）對(duì)于AES算法中的MixColumns操作，該操作需對(duì)同一列中不同行的字節(jié)進(jìn)行混合，操作過(guò)程中相同的掩碼值相互抵消就會(huì)暴露中間值。因此，為了確保所有的中間值都能夠被掩碼，本文對(duì)該處算法狀態(tài)的每一行都采用一個(gè)單獨(dú)的掩碼值進(jìn)行掩碼。預(yù)先計(jì)算p組單字節(jié)掩碼值R={m0，m1，…，mp-1}及其經(jīng)過(guò)MixColumns操作后的相對(duì)應(yīng)的輸出掩碼值R，={m’0，m’1，…，m’p-1}，將其存儲(chǔ)在 ROM 中，每輪加密運(yùn)算時(shí)，從R中隨機(jī)選取4個(gè)，對(duì)狀態(tài)字節(jié)的每一行分別進(jìn)行掩碼，操作結(jié)束后再用相對(duì)應(yīng)的R，來(lái)消除掩碼。列混淆操作的具體掩碼過(guò)程如圖2所示。

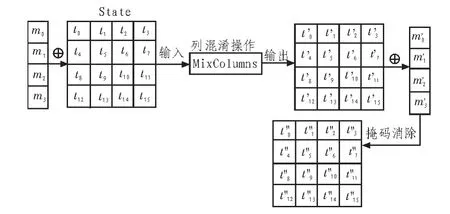
圖2 列混淆操作的掩碼過(guò)程Fig.2 Masking process of MixColumns operation

3.2 改進(jìn)的掩碼防御方案性能分析

公設(shè)：設(shè)密碼運(yùn)算過(guò)程中變量 z1，z2，…，zn，如果存在一個(gè)函數(shù) f能夠使得等式 z=f（z1，z2，…，zn）成立，則稱可以實(shí)施高階功耗攻擊。

文中的改進(jìn)掩碼算法中，所有的中間值均被掩碼，所以一定能夠抵抗一階SPA和DPA攻擊。同時(shí)，對(duì)加密算法的每輪4個(gè)函數(shù)操作均采取不同的掩碼值集合進(jìn)行掩碼，因而不存在中間變量滿足 z=f（z1，z2，…，zn），所以該算法能夠防御二階DPA攻擊。

文中提出的改進(jìn)算法需要4個(gè)寄存器來(lái)存儲(chǔ)四輪運(yùn)算的掩碼值集合，并且需要完成對(duì)掩碼型S盒和MixColumns操作的預(yù)計(jì)算，對(duì)內(nèi)存的需求有所增加，但該方法實(shí)現(xiàn)簡(jiǎn)單，更容易實(shí)現(xiàn)硬件電路的設(shè)計(jì)。與文獻(xiàn)[6]中的方法相比，本文增加了一個(gè)MixColumns的預(yù)計(jì)算和存儲(chǔ)，對(duì)MixColumns操作的狀態(tài)字節(jié)分行掩碼，進(jìn)一步提高了算法抗二階DPA攻擊的安全性。許多文獻(xiàn)提出的抗高階能量分析方法都是針對(duì)高階S盒的設(shè)計(jì)[1，8]，由于S盒非線性函數(shù)的特性，這類方法的實(shí)現(xiàn)過(guò)程比較復(fù)雜，對(duì)硬件電路設(shè)計(jì)的要求也比較高。因此，本文提出的算法在保證安全性的同時(shí)更具可行性。

4 實(shí)驗(yàn)結(jié)果分析

文中用FPGA實(shí)現(xiàn)了文獻(xiàn)[7]提出的固定值掩碼方法和本文提出的掩碼方法，搭建能量分析平臺(tái)，在加密算法執(zhí)行期間，F(xiàn)PGA向數(shù)字示波器發(fā)送觸發(fā)信號(hào)，采集采樣電阻兩端的能量消耗曲線，并將數(shù)據(jù)傳送到計(jì)算機(jī)，計(jì)算機(jī)運(yùn)用MATLAB軟件對(duì)采集到的數(shù)據(jù)進(jìn)行統(tǒng)計(jì)分析，從而獲得相關(guān)的密鑰信息。本文通過(guò)對(duì)5 000條明文進(jìn)行加密，得到能量消耗數(shù)據(jù)，統(tǒng)計(jì)分析后得到的結(jié)果如圖3和圖4所示。實(shí)驗(yàn)證明兩種方法均可以抵抗一階SPA攻擊和DPA攻擊，但文獻(xiàn)[7]中提出的掩碼算法并不能完全抵抗二階DPA攻擊，圖3中的尖峰表示該掩碼方案中存在著中間值未被掩碼，從而導(dǎo)致信息泄漏，攻擊者可以從中猜測(cè)出正確的密鑰。而圖4則表明了本文提出的改進(jìn)的固定值掩碼算法能夠抵抗二階差分能量分析攻擊。

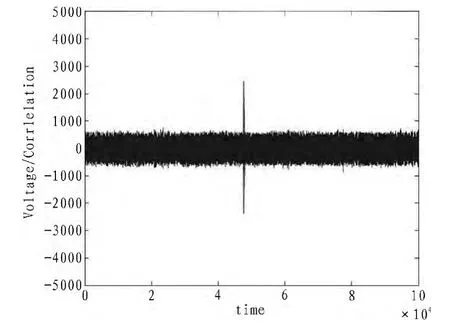
圖3 文獻(xiàn)[7]中掩碼方案二階差分能量攻擊結(jié)果Fig.3 Results of masking method in ref.[7]for second-order DPA attacks

圖4 本文改進(jìn)掩碼方法二階差分能量攻擊結(jié)果Fig.4 Results of the improved masking method in this paper for second order DPA attacks

5 結(jié) 論

能量分析攻擊由于其成本消耗低，攻擊效率高等特點(diǎn)，已成為當(dāng)今智能卡等嵌入式設(shè)備安全最大的威脅。智能卡等設(shè)備由于其自身資源的有限性，因此，采用固定值掩碼方案來(lái)抗能量攻擊是一種比較實(shí)用可行的方法。固定值掩碼方法相對(duì)于隨機(jī)掩碼算法來(lái)說(shuō)，占用了更少的資源，實(shí)現(xiàn)了更快的加解密速度。

然而，隨著攻擊技術(shù)的不斷發(fā)展，各類攻擊方法越來(lái)越復(fù)雜多樣，有些算法已經(jīng)不能達(dá)到實(shí)際應(yīng)用中的安全要求。所以，我們需要對(duì)固定值掩碼方法進(jìn)一步地研究與改進(jìn)，以提高其抗高階能量分析攻擊的能力。

本文對(duì)固定值掩碼方案進(jìn)行了深入地研究，并在此基礎(chǔ)上提出了一種改進(jìn)的固定值掩碼方法，進(jìn)一步的工作是實(shí)現(xiàn)對(duì)掩碼型加密算法的優(yōu)化，以及其在智能卡等設(shè)備上的硬件實(shí)現(xiàn)[9-10]。

[1]Rivain M，Prouff E.Provably Secure Higher-Order Masking of AES[C]//In:Mangard S， Standaert F-X （eds.） CHES 2010.LNCS，Springer，Heidelberg，2010:413-427.

[2]Fumaroli G，Martinelli A，Prouff E，Rirain M.Affine Masking against Higher-Order Side Channel Analysis[C]//In selected Areas in Cryptography， ser.LNCS， vol.6544.Springer，2010:262-280.

[3]A M-L，Giraud C.An Implementation of DES and AES，Secure against Some attacks [A].In:Workshop on Cryptographic Hardware and Embedded Systems CHES 2005， LNCS 2163[C]//Berlin:Springer-Verlag，2005:309-318.

[4]Mehd I，Laurent Akker，Giraud C.An Implemention of DES and AES，Secure against Some Attacks[A].Workshop on Cryptographic Hardware and Embedded Systems CHES 2001[C].Springer-Verlag，2001.

[5]Golic J D，Tymen C.Multiplicative Masking and Power Analysis of AES[A].Workshop on Cryptographic Hardware and Embedded Systems CHES 2002[C]//Lecture Notes in Computer Science.Volume 2623.Springer-Verlag，2003:198-212.

[6]Messerges Thomas S.Securing the AES Finalists Against Power Analysis Attacks[C].Proceedings of Fast Software Encryption Workshop 2000， Spinger-Verlag，2000.

[7]李浪.簡(jiǎn)單固定值掩碼二階差分功耗攻擊方法及其防御措施[J].小型微型計(jì)算機(jī)系統(tǒng)，2010，31（9）:1894-1898.LI Lang.Simple fixed value masking for second-order differential power attack methods and its defense measures[J].Small Microcomputer System， 2010，31（9）:1894-1898.

[8]Ahmed W，mahmood H，Siddique U.The Efficient Implementation of S8 AESAlgorithm[J].Proceedings of the World Congress on Engineering，2011，WCE 2011:1215-1219.

[9]Regazzoni F，Wang Y，Standaert F.FPGA Implementation of the AES Masked Against Power Analysis Attacks[C]//In COSADE， February，2011:56-66.

[10]Genelle L， Prouff E， Quisquater M.Montgomery’s trick and fast implementation of masked AES[C].In:Nitaj， A.，Pointcheval， D.（eds.）AFRICACRYPT 2011.:153-169.