不規則波中船舶參數橫搖的概率分析

張曉，楊和振

1 海洋工程國家重點實驗室，上海200240

2 上海交通大學船舶海洋與建筑工程學院，上海200240

0 引 言

在動力系統中，隨時間變化的參數會導致參量不穩定問題發生［1］。當船舶在波浪中迎浪運動時，經過船體中剖面的波高會隨時間變化，從而導致船舶水線面面積隨著時間不斷變化，船舶初穩性高也隨之變化，這種時變的初穩性高使得船舶處于參量不穩定區域，激勵船舶發生大角度橫搖，也即所說的船舶參數橫搖。

為了獲得較大的裝載空間，運輸汽車貨車專用船、滾裝船［2］和集裝箱船［3］通常具有較大的艏艉外飄，其型線使得船舶在波浪中的時變初穩性高變化更為劇烈，從而使船舶更易發生參數橫搖。近年來的一些集裝箱船事故均與船舶參數橫搖有關。1998年，由高雄開往西雅圖的一艘巴拿馬型集裝箱船發生了30°的大角度橫搖，致使集裝箱落水并受損［3］；而另一艘集裝箱船在經歷了大角度橫搖后，同樣遭遇了集裝箱的丟失和破壞［4］。在這兩起事故中，大角度橫搖主要與船舶在惡劣海況下的參數橫搖有關［3-4］。

在實際航行過程中，船舶的時變穩性高是隨波浪而隨機變化的，此時的船舶參數橫搖是一個非線性的隨機過程。張壽桂［5］對發生大傾角橫搖時的穩性力臂予以了研究。雖然隨機波浪中的船舶參數橫搖已由實驗證實［3，6-7］，但其機理和特征還有待進一步的探討。本文將從概率的角度研究不規則波中迎浪船舶的參數橫搖，利用橫搖角頻率分布直方圖描述時域橫搖角的分布，并通過橫搖角的分布情況來評估船舶航行的危險程度。為了探討運動方程初值對橫搖運動的影響，擬計算200 組數值以模擬不同時刻的橫搖角標準差。

1 方法介紹

1.1 運動方程

船舶參數橫搖的早期研究是基于馬修方程［8-9］。隨著研究的進展，為了進一步探討參數橫搖的特性，引入了阻尼項和非線性回復力矩。Yang 等［10］利用Hill 方程研究了不規則波中立管的參量不穩定性問題。本文以一艘巴拿馬型集裝箱船為例，采用具有線性阻尼、非線性阻尼和非線性回復力矩的橫搖運動方程，利用概率統計的方法，對不規則波中船舶參數橫搖進行了探討。

不規則波中的船舶參數橫搖運動可以采用下述運動方程描述：

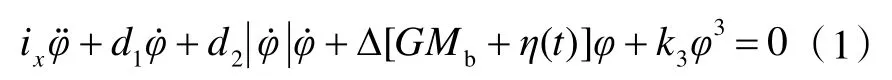
式中：ix為船舶橫搖慣性矩和附加質量；d1為船舶橫搖線性阻尼；d2為船舶橫搖非線性阻尼；GMb為靜水初穩性高；k3為非線性回復力矩系數；φ 為船舶橫搖運動橫搖角；η(t)為隨機波浪作用下初穩性高的波動項。規則波中初穩性高的波動是按照正弦函數的規律變化，不規則波中初穩性高的波動是一個時間的函數，形式更復雜。對于運動方程的求解，本文采用變步長Runge-Kutta法，在求解運動方程并得到橫搖運動橫搖角的基礎上，對船舶運動的橫搖角進行概率分析。

1.2 Grim 有效波理論

本文通過Bretchneider 波譜產生不規則波，Bretchneider 波譜以有義波高和譜峰周期為輸入參數。Bretchneider波譜的公式如下：

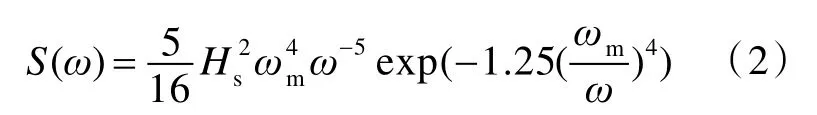
式中：HS為船舶的有義波高；ωm為譜峰周期；ω為不規則波浪頻率。

在所產生的不規則波譜的基礎上，本文通過Grim 有效波理論對不規則波進行了簡化處理。Grim 有效波理論由Grim 于1961年提出，該方法是使用與船長同長度的單波來表示通過船體的不規則波。從工程的角度看，Grim 有效波理論是一種合理的簡化方法，并且已經應用于船舶參數橫搖的相關研究［11］。

1.3 概率分析方法

圖1 描述了船舶在不規則波中參數橫搖運動橫搖角的時域變化。不同的橫搖角時域圖因其非線性和隨機性而有著顯著的差別，其時域圖復雜又沒有規律，為了使分析更簡明，更好地表示橫搖角的分布規律，評估船舶運動的危險程度，采用了橫搖角頻率分布直方圖，如圖2 所示。其通過統計各個角度范圍出現的頻率來評估船舶在運動過程中的危險程度，和橫搖角時域運動圖相比，頻率分布直方圖更為簡潔地描述了船舶在運動過程中橫搖角的變化與分布情況。

為了分析不同運動方程初值的影響，對200組模擬了不同時刻的橫搖角標準差進行了計算。標準差是離均差平方和平均后的方根，反映了數據集的離散程度。標準差可由如下公式計算：

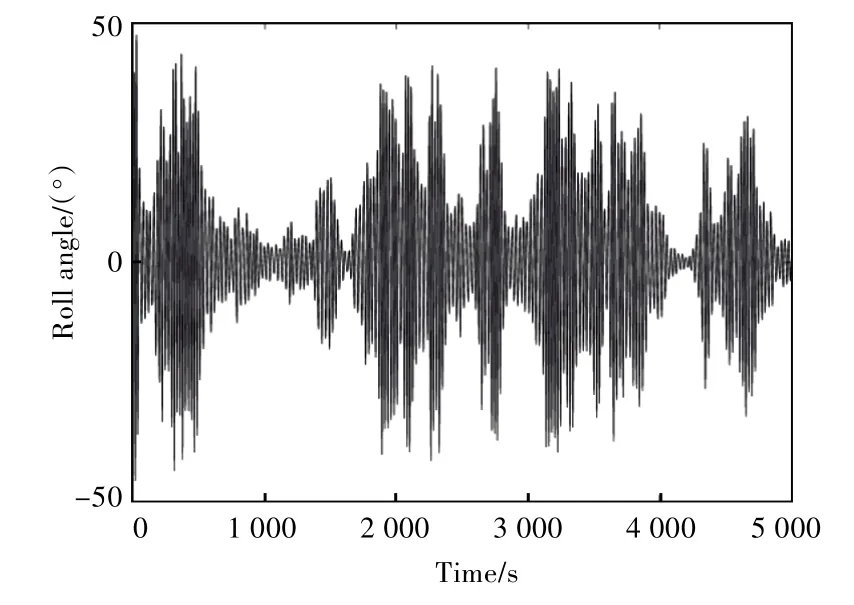
圖1 不規則波中橫搖角隨時間變化的曲線Fig.1 Roll angles in irregular wave at different time

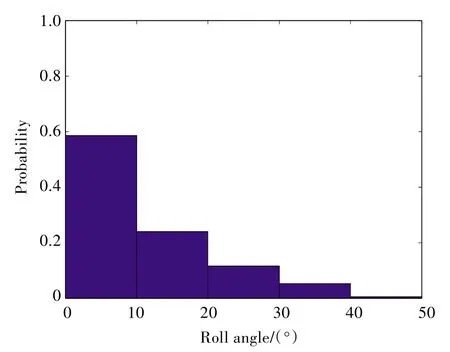
圖2 不規則波中橫搖角頻率分布直方圖Fig.2 Histogram of frequency distribution for roll angles in irregular wave

式中：N 為樣本容量；xi為樣本數據；u 為樣本均值。

關于標準差在不規則波參數橫搖分析中的應用，將在第2.2 節具體闡述。

2 算例分析

本文以一艘巴拿馬型集裝箱船為例，對其在波浪中運動時的參數橫搖進行了分析，該船的主尺度如表1所示。

表1 集裝箱船主尺度Tab.1 Main dimensions of the container ship

2.1 規則波中船舶參數橫搖

假設規則波中的船舶初穩性高按照正弦形式變化。圖3 所示為規則波中橫搖角φ 隨時間變化的曲線。從中可以看出，當t＞300 s 后，運動趨于穩定，而在此之前，橫搖角的變化可以認為是從初值到穩定運動的過渡階段。圖4 所示為規則波中橫搖幅值的包絡線。規則波中的參數橫搖可以用數值進行模擬，橫搖角是從運動方程給定初值，經過過渡階段而到達穩定值，穩定值達25 °。在數值模擬過程中，確實存在著由參數激勵而導致的大角度橫搖。

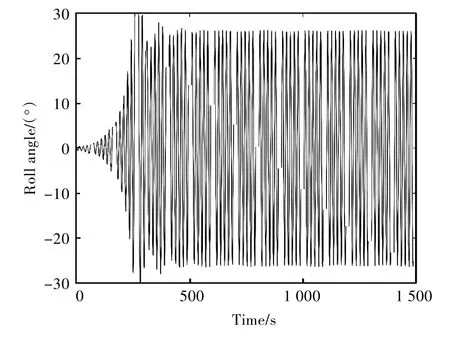
圖3 規則波中橫搖角隨時間變化的曲線Fig.3 Rroll angles in regular wave at different time

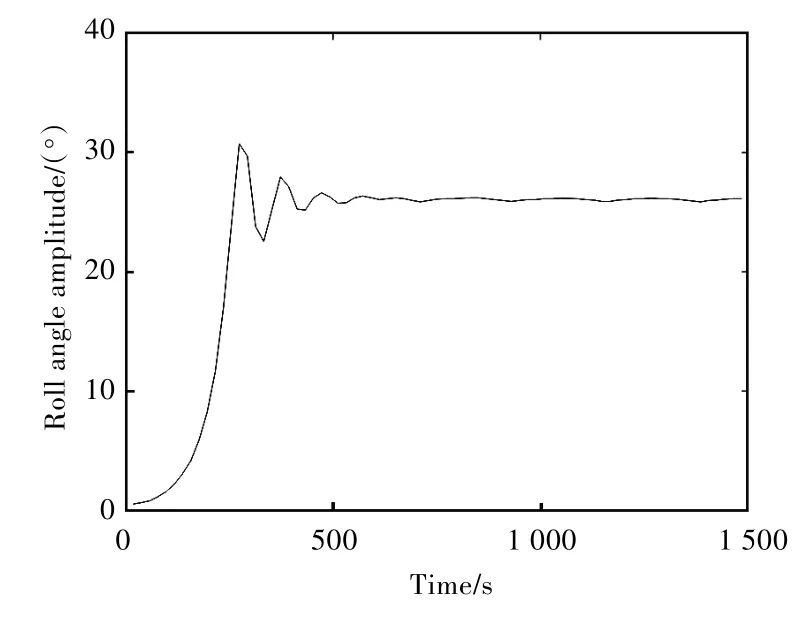
圖4 規則波中橫搖幅值包絡線Fig.4 Envelope of roll angle amplitudes in regular wave

2.2 不規則波中船舶參數橫搖

圖5～圖7 所示分別為不規則波下初始橫搖角速度為0，5，10（°）/s 時，橫搖角隨時間變化的曲線。對比圖5 ～圖7 可以看出，運動方程的初值不同，得到的時域橫搖角曲線也不同。從數值模擬的角度研究船舶參數橫搖，發現不同的初值會導致不同的運動特征。對于不規則波中的船舶參數橫搖，本文將從概率的角度進行統計分析。

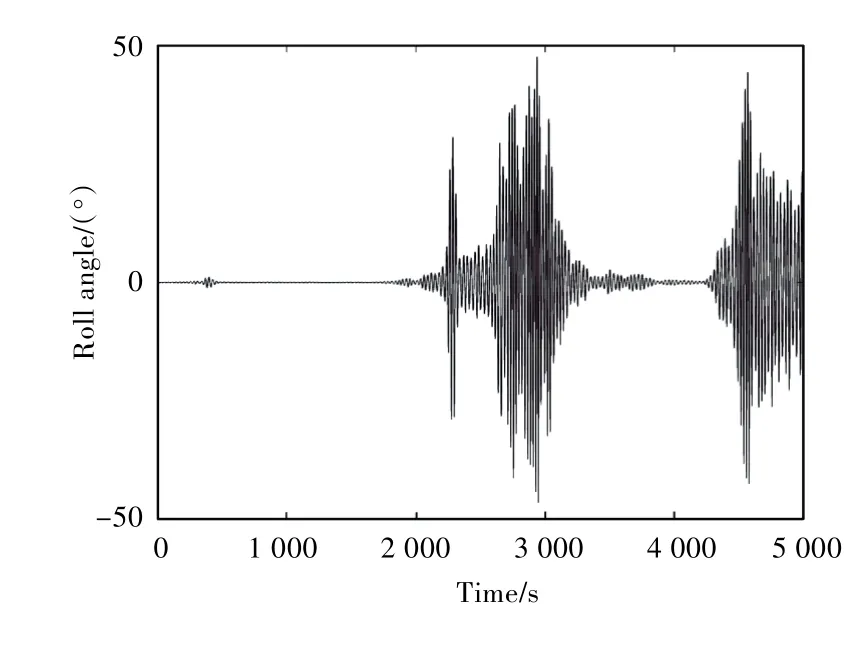
圖5 初始橫搖角速度為0（°）/s時不規則波中橫搖角隨時間變化的曲線Fig.5 Roll angles in irregular wave at different time（initial angular velocity of motion equation is 0（°）/s）

圖6 初始橫搖角速度為5（°）/s 時不規則波中橫搖角隨時間變化的曲線Fig.6 Roll angles in irregular wave at different time（initial angular velocity of motion equation is 5（°）/s）

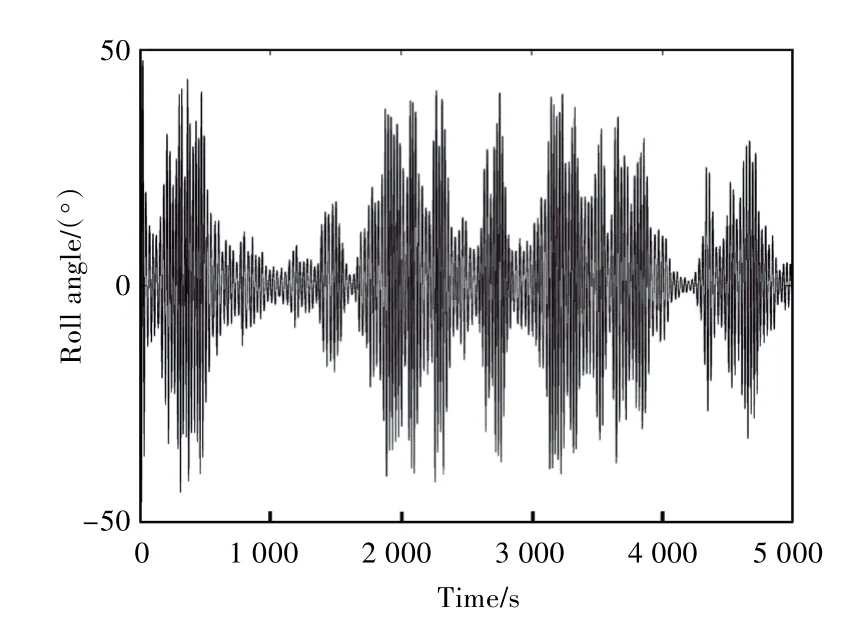
圖7 初始橫搖角速度為10（°）/s時不規則波中橫搖角隨時間變化的曲線Fig.7 Roll angles in irregular wave at different time（initial angular velocity of motion equation is 10（°）/s）

繪制不規則波下的橫搖角頻率分布直方圖，以探討在不同初值下橫搖角的概率分布有否不同。圖8～圖10 所示分別為不規則波下初始橫搖角速度為0，5，10（°）/s 時，橫搖角的頻率分布直方圖。可以通過概率分布直方圖中不同橫搖角出現的概率大小來評估船舶航行的危險程度。從圖中可以發現，初值不同，不規則波中橫搖角的頻率分布直方圖也有所不同。

圖8 初始橫搖角速度為0（°）/s 不規則波中橫搖角頻率分布直方圖Fig.8 Histogram of frequency distribution for roll angles in irregular wave（initial angular velocity of motion equation is 0（°）/s）

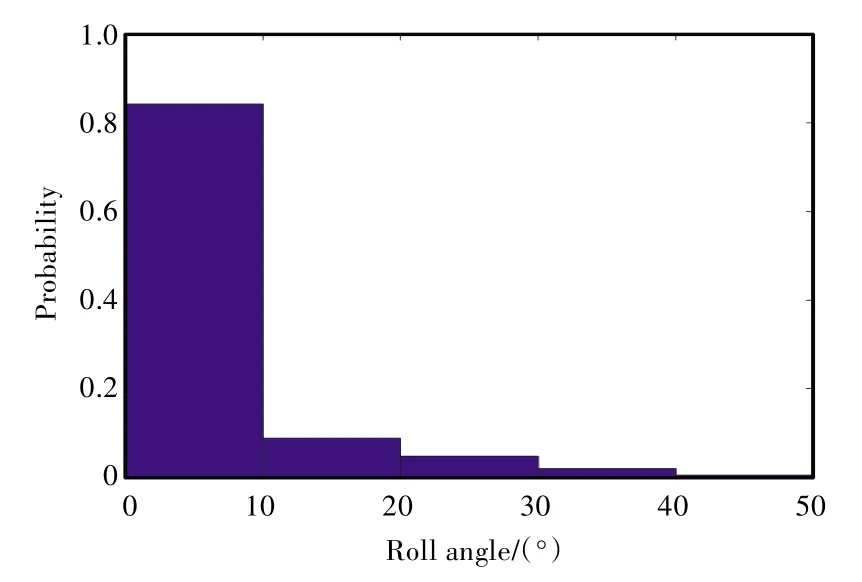
圖9 初始橫搖角速度為5（°）/s不規則波中橫搖角頻率分布直方圖Fig.9 Histogram of frequency distribution for roll angles in irregular wave（initial angular velocity of motion equation is 5（°）/s）

圖10 初始橫搖角速度為10（°）/s 時不規則波中橫搖角頻率分布直方圖Fig.10 Histogram of frequency distribution for roll angles in irregular wave（initial angular velocity of motion equation is 10（°）/s）

船舶在實際航行時與數值模擬不同，數值模擬需要給出運動方程的初始角和初始橫搖角速度，而初值的不同會造成橫搖運動不同，繼而得到的橫搖角頻率分布直方圖也不同。為了忽略運動方程初值的影響，在進行概率分析時，不能采用初始時間段的橫搖角數據，合適的初始時間段可以根據初值的不同予以選取。

每個初值選取200 組數值進行模擬，每組模擬5 000 s，計算每一時刻橫搖角的標準差。圖11～圖13 所示分別為初始橫搖角速度為0，5，10（°）/s 時不同時刻的橫搖角標準差。

由圖11～圖13 可以看出，初值不同，橫搖角標準差隨時間變化的趨勢也不同，但經過一段時間后，相對于開始時間段，橫搖角標準差要更加穩定。當初始橫搖角速度為0（°）/s 時，在時間t＞3 000 s 之后，橫搖角標準差趨于穩定，因此可以采用3 000 s 之后的橫搖角數據，以降低運動方程初始值對橫搖角概率統計分析的影響。而當初始橫搖角速度為5，10（°）/s 時，在時間t＞1 000 s 之后，橫搖角標準差趨于穩定，因此可以采用1 000 s之后的橫搖角數據，以降低運動方程初始值對橫搖角概率統計分析的影響。

圖11 初始橫搖角速度為0（°）/s時不同時刻的橫搖角標準差Fig.11 Standard deviation of roll angles at different time（initial angular velocity of motion equation is 0（°）/s）

圖12 初始橫搖角速度為5（°）/s時不同時刻的橫搖角標準差Fig.12 Standard deviation of roll angles at different time（initial angular velocity of motion equation is 5（°）/s）

3 結 論

作為船舶失穩的重要模式，探討參數橫搖對于船舶安全航行具有重要意義。本文從概率的角度探討了不規則波中的船舶參數橫搖，從以上計算和分析可以得到如下結論：

1）可以通過頻率分布直方圖分析不規則波中的參數橫搖。和時域橫搖角變化圖相比，頻率分布直方圖更為簡潔，可以通過分析不同橫搖角出現的概率來評估船舶運動的危險程度。

2）運動方程的初值會影響船舶橫搖運動的概率分析結果。初值不同，其時域運動不同，頻率分布直方圖也不同。為了排除運動方程初值對概率分析的影響，應該選取合適時間段內的橫搖角數據，而合適的時間段則可以根據初值的不同來選取。

［1］楊和振，李華軍. 參數激勵下深海立管動力特性研究［J］.振動與沖擊，2009，28（9）：65-69，78.YANG Hezhen，LI Huajun. Vibration analysis of deep-sea risers under parametric excitations［J］. Jour?nal of Vibration and Shock，2009，28（9）：65-69，78.

［2］HUA J B，WANG W H.Roll motion of a roro-ship in ir?regular following waves［J］. Journal of Marine Science and Technology，2001，9（1）：38-44.

［3］FRANCE W N，LEVADOU M，TREAKLE T W，et al.An investigation of head-sea parametric rolling and its influence on container lashing systems［J］. Marine Technology，2003，40（1）：1-19.

［4］CARMEL S M. Study of parametric rolling event on a panamax container vessel［J］. Transportation Research Record：Journal of the Transportation Research Board，2006（1）：56-63.

［5］張壽桂. 船舶在大風浪中橫搖穩性變化的理論研究［J］.中國艦船研究，2006，1（1）：50-53.ZHANG Shougui. Theoretical study method for roll sta?bility of ships in waves［J］. Chinese Journal of Ship Research，2006，1（1）：50-53.

［6］LU J，UMEDA N，MA K. Predicting parametric rolling in irregular head seas with added resistance taken into account［J］. Journal of Marine Science and Technolo?gy，2011，16（4）：462-471.

［7］PARK D M，KIM Y，SONG K H. Sensitivity in numeri?cal analysis of parametric roll［J］. Ocean Engineering，2013，67：1-12.

［8］FRANCE W N，LEVADOU M，TREAKLE T W，et al. An investigation of head-sea parametric rolling and its influence on container lashing systems［J］. Marine Technology，2003，40（1）：1-19.

［9］GRAFF W，HECKSCHER E. Widerstands-und stabil?it?ts-versuche mit drei fischdampfermodellen［J］.Werft-Reederei-Hafen，1941，22：115-120.

［10］YANG H Z，XIAO F，XU P J. Parametric instability prediction in a top-tensioned riser in irregular waves［J］.Ocean Engineering，2013，70：39-50.

［11］HASHIMOTO H，UMEDA N. Nonlinear analysis of parametric rolling in longitudinal and quartering seas with realistic modeling of roll-restoring moment［J］.Journal of Marine Science and Technology，2004，9（3）：117-126.