超高分子量聚乙烯纖維增強層合厚板抗高速鈍頭彈侵徹的理論模型

陳長海，徐文獻，朱錫，侯海量

1 海軍工程大學艦船工程系，湖北武漢430033

2 海軍湛江地區裝備修理監修室，廣東湛江524005

0 引 言

超高分子量聚乙烯（UHMWPE）纖維由于具有防彈性能好及密度低等優點，近年來在防護領域得到了廣泛的關注。關于超高分子量聚乙烯纖維增強塑料（UFRP）層合板的抗侵徹機理問題，國內外的學者們開展了大量的試驗研究［1-6］，并給出了在一定速度范圍內UFRP 層合板的彈道吸能［1］或彈道極限［5-6］隨靶板面密度變化的經驗關系式。然而，這些經驗關系式針對的都是特定的彈靶系統，具有一定的局限性。

受層合板纖維的韌脆特性以及靶板厚薄等因素的影響，致使不同類型層合板在抗侵徹過程中的破壞模式及吸能機理差異較大，因而很難建立適合不同類型層合板的理論模型。早期層合板的抗侵徹理論模型大多是基于單一的變形模式及特定的彈靶系統，主要分為針對脆性中厚層合板［7-9］的理論模型和針對韌性層合薄板［10-12］的理論模型2 大類。梅志遠等［13］基于纖維增強復合材料（FRC）層合板抗高速侵徹的變形和破壞模式分析，提出了兩階段理想侵徹模型，并指出該模型適用于不同類型的FRC 層合板。然而，從與該文試驗結果的比較可看出，文獻［13］中的模型對于韌性FRC 層合板的適用性要好于脆性FRC 層合板。

在對大量UFRP 抗侵徹試驗研究結果［1-6］進行分析的基礎上，陳長海等［14］提出了鈍頭彈高速侵徹中厚UFRP 層合板的三階段理論模型，理論計算值與相關文獻試驗結果吻合較好。但文獻［14］中的模型對于UFRP 層合厚板抗高速侵徹的情形不能進行很好的計算和預測，例如，不能計算UFRP 層合厚板未穿透情形下的彈體總侵徹深度（depths of penetration，DOP）以及存在層合厚板彈道極限預測值偏高等問題。基于此，本文將結合UFRP 層合厚板抗高速侵徹的特點，通過改進開坑鐓粗階段的計算方法和拉伸變形階段的計算過程，建立UFRP 層合厚板抗鈍頭彈高速侵徹的理論模型，然后利用該模型計算彈體侵徹深度和層合厚板的彈道極限速度，并與相關文獻試驗結果進行比較，以驗證模型的實用性和有效性。

1 侵徹過程分析

相關的試驗研究結果表明［1-6］，UFRP 層合厚板在抗高速侵徹的過程中，其迎彈面會產生纖維熔斷，厚度方向會呈現剪切和拉伸變形這2 種失效模式。另外，彈體在侵徹的過程中其頭部會出現明顯的鐓粗變形。因此，將UFRP 層合厚板的抗侵徹過程分為3 個階段，如圖1 所示。圖中Hp為變形錐的高度。

開坑鐓粗階段是UFRP 層合厚板抗高速侵徹的第1 個階段。在開坑鐓粗階段，層合板迎彈面侵徹區近似呈現流體動力狀態，熔斷纖維及碎裂基體由于彈體的擠壓作用會向抗力最小的方向，即反向飛濺噴出，從而出現試驗中的反向噴射現象。當彈體速度與接觸界面的運動速度一致時，開坑鐓粗階段結束（圖1（a））。開坑鐓粗階段結束后，UFRP 層合厚板即進入剪切壓縮階段（圖1（b）），而剪切壓縮階段結束后，層合厚板則進入拉伸變形階段（圖1（c））。剪切壓縮階段和拉伸變形階段的UFRP 層合厚板受力狀態與中厚板［14］相同。

2 各階段吸能計算

2.1 開坑鐓粗階段

在文獻［14］的理論模型中，壓縮鐓粗階段（即本文的開坑鐓粗階段）的侵徹深度取的是層合板總厚度的0.1 倍，這是基于試驗結果得到的，即在試驗結果的基礎上，通過對相同厚度層合板在不同侵徹速度下各次試驗結果取平均值而得到。雖然該壓縮鐓粗階段侵徹深度的取法具有一定的合理性，也在一定程度上體現了彈體速度以及彈靶材料的影響，但隨著層合板厚度的增加，穿透層合板所需的彈丸初速（即層合板的彈道極限）也會相應提高。因此在一定穿透速度范圍內，隨著層合板厚度的增加，壓縮鐓粗階段的侵徹深度會相應增大，從而表現出侵徹深度隨層合板厚度的變化現象，文獻［5-6］的試驗結果也證實了這一點。由此可見，文獻［14］中壓縮鐓粗階段侵徹深度的取法存在一定的局限性，不能很好地體現彈丸初速侵徹速度的影響。為進一步提高理論模型的適用性和普適性，本文對UFRP 層合厚板抗鈍頭彈高速侵徹的初期，即開坑鐓粗階段的計算方法進行了改進，以期能對UFRP 層合厚板抗鈍頭彈高速侵徹的情形進行合理、準確的計算和預測。

在開坑鐓粗階段，UFRP 層合厚板迎彈面會出現纖維熔斷和基體碎裂現象，同時彈丸頭部會產生一定程度的鐓粗變形，且鐓粗變形程度會隨彈體侵徹速度的增大而變大。假設彈體的鐓粗變形僅發生在開坑鐓粗階段，開坑鐓粗階段結束后，認為彈體頭部不再發生鐓粗變形。對于類似于金屬靶板的彈體鐓粗問題，可將層合板看做可變形的靶板，彈體高速侵徹可變形靶板的過程如圖2 所示。圖中：l 和lp分別為彈體剛性區（未變形區）和塑性區（變形區）的長度；h 為彈體侵入靶板的深度；u 為塑性界面向左傳播的速度；v 為彈體剛性區的運動速度（即彈體的運動速度）；vc為彈靶接觸界面的運動速度；A0為未變形區截面積；A為變形區截面積。

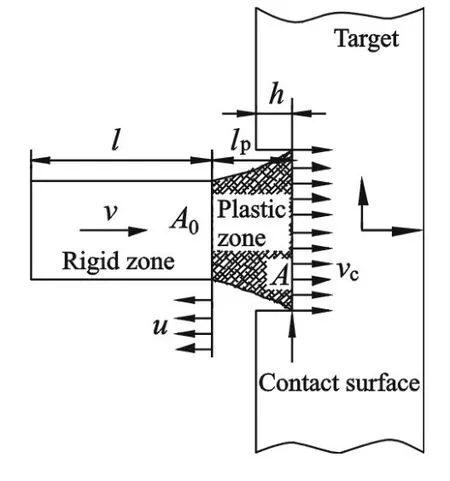
圖2 彈體撞擊可變形靶板示意圖Fig.2 Schematic of projectile impacting on deformable target

對于彈體，根據動量沖量守恒，可得dt 時間內彈體動量轉化為塑性區中壓縮沖量的增量I 為

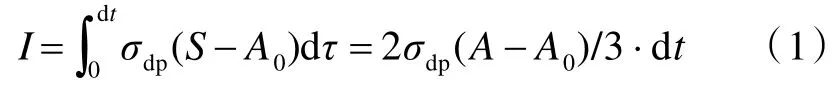
式中，S 為截面積的積分符號。

對于彈靶接觸界面，根據動量沖量守恒定律，有

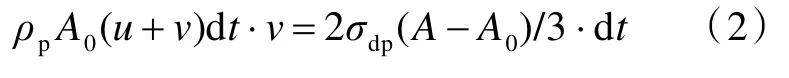
式中，ρp和σdp分別為彈體的質量密度與動屈服強度。

通過推導、代換、整理后，可得彈體鐓粗后的直徑d1和截面面積A1分別為：

式中，e=λ+1+(λ2+2λ)0.5，其中v0為彈體初速，K=1+(ρpcp)/(ρtct)，而ρt為靶板的質量密度，cp和ct分別為壓縮應力波在彈體與靶板中的傳播速度。

設彈靶接觸界面的接觸應力為σj，彈體由于接觸應力作用而引起的向左后退的速度為v1，靶體由于接觸應力作用而引起的向右運動的速度為v2（即接觸界面的運動速度vc），則有vc=v2=v0-v1。根據撞擊時的動量沖量守恒定律，可得彈靶接觸界面的運動速度為［15］

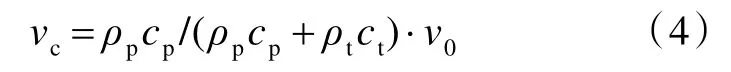
開坑鐓粗階段結束時，彈體速度v1=vc。因此，該階段的總耗能W1為

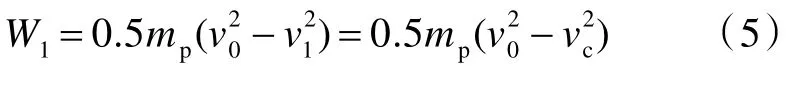
式中，mp為彈體質量。

在開坑鐓粗階段，彈體的侵徹時間為t1，因而可得開坑鐓粗階段彈體的侵徹深度h1為

2.2 剪切壓縮階段

剪切壓縮階段分初始壓縮波的傳播和反射拉伸波的反向傳播2 個子階段。

在初始壓縮波傳播子階段，層合板的壓縮耗能Wc21和剪切耗能Ws21分別為［14］：

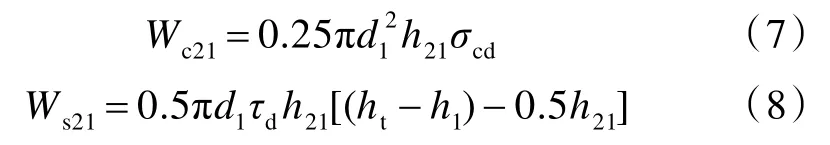
式中，σcd和τd分別為層合板的動壓縮反力和動剪切反力；ht為層合板的總厚度；h21為初始壓縮波傳播子階段的侵徹深度。

在初始壓縮波傳播子階段，彈體的運動方程為

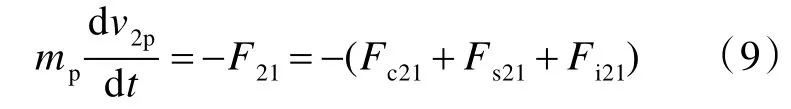
式中，v2p，F21，Fc21，Fs21和Fi21分別為初始壓縮傳播子階段彈體的瞬時速度、層合板的總抗力、壓縮反力、剪切反力和侵徹區慣性反力。各反力的表達式可參見文獻［14］。

令v2p=v2p(t)，則在初始壓縮波傳播子階段，彈體的侵徹深度h21為

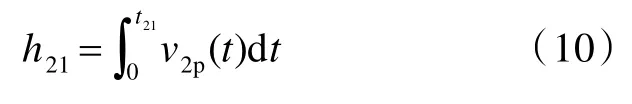
在反射拉伸波傳播子階段，層合板的壓縮耗能Wc22和剪切耗能Ws22分別為［14］：

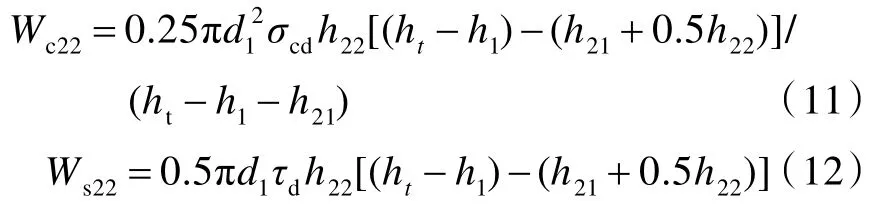
在反射拉伸波傳播子階段，彈體的運動方程為

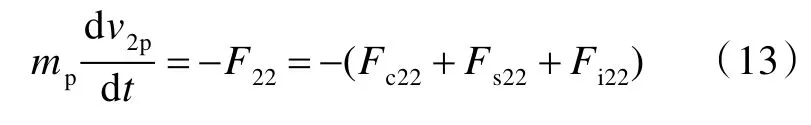
式中，F22，Fc22，Fs22和Fi22分別為反射拉伸波傳播子階段層合板的總抗力、壓縮反力、剪切反力和侵徹區慣性反力。各反力的表達式可參見文獻［14］。

在反射拉伸波傳播子階段，彈體的侵徹深度h22為

因此，剪切壓縮階段彈體的總侵徹深度h2為

剪切壓縮階段彈體損失的總動能，即層合板吸收的總能量W2為

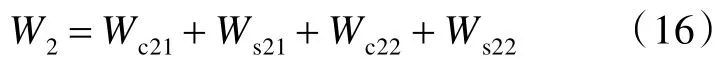
2.3 拉伸變形階段

拉伸變形階段也分2 個子階段，即變形錐的形成及擴展子階段與變形錐纖維層逐步失效子階段。變形錐的形成及擴展子階段從變形的形成開始，至變形錐達到極限變形狀態，該狀態下的變形錐角滿足條件

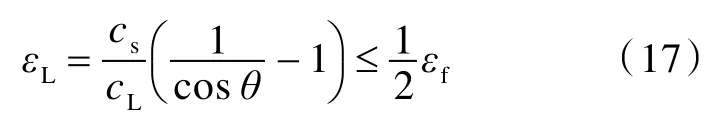
式中：εL和εf分別為纖維層的平均應變和拉伸失效應變；cs和cL分別為層合板的剪切應力波速和拉伸應力波速。由此，可得變形錐的極限變形錐角θε為

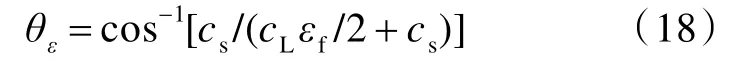
變形錐形成及擴展子階段的吸能主要包括過渡區分層吸能Ede31和變形錐彈性變形能EED，分別為［14］：

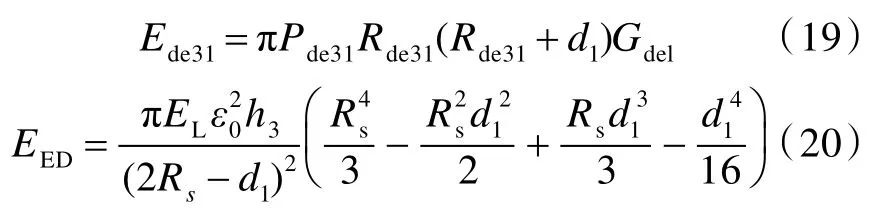
式中：Pde31為分層折減系數；Gdel為層合板層間斷裂韌性值；Rde31為裂紋傳播半徑，Rde31=cdelt31，其中cdel為層間裂紋傳播速度；Rs取為變形錐擴展至極限狀態時的錐半徑值；EL為層合板的拉伸模量；ε0為侵傾區邊緣，即r=d1/2 處纖維層的應變，當變形錐達到極限狀態時，有ε0=εf；h3為層合板背層未穿透纖維層的厚度，h3=ht-h1-h2。在變形錐纖維層逐步失效子階段，由于彈體的動能不足以使變形錐所有的纖維層全部失效，即不能穿透層合板，因而出現了部分侵徹的情形（圖1（d））。令該子階段失效纖維層的厚度為h3p，則變形錐侵徹區纖維層的拉伸斷裂吸能ETF為［14］

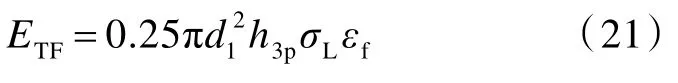
式中，σL為層合板纖維層拉伸強度。此外，變形錐失效纖維層在彈體侵徹過程中還存在分層吸能［14］：

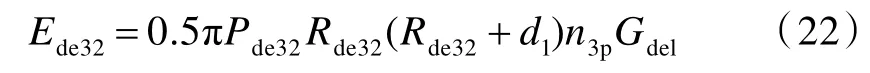
式中：Pde32為分層折減系數；Rde32為裂紋傳播半徑，Rde32=cdelt32；n3p為變形錐失效纖維層層數，n3p=N·h3p/ht，其中N 為層合板總層數。

由此可得拉伸變形階段彈體損失的總動能，即層合板吸收的總能量W3為

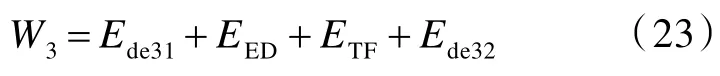
在拉伸變形階段，彈體的侵徹深度即為變形錐失效纖維層的厚度h3p。

3 彈體侵徹深度計算

在拉伸變形階段的第1 個子階段，即變形錐的形成及擴展子階段，在變形錐未達到極限變形錐角之前，隨著彈體的運動，變形錐錐頂會向前運動一定的距離，但在此子階段，變形錐纖維層并未失效，彈體并未穿透纖維層。因此，為與彈體侵徹深度的一般定義相一致，本文彈體的侵徹深度定義為由彈體侵徹所引起的失效纖維層（包括基體）的總厚度。主要計算過程如下：

1）計算得到開坑墩粗階段的侵徹深度h1。

2）在剪切壓縮階段，先對初始壓縮波傳播子階段進行計算，得到該子階段的侵徹深度h21。在初始壓縮波傳播子階段，若彈體的速度等于0，則彈體總的侵徹深度Dp=h1+h21；初始壓縮波傳播子階段結束后，若彈體的速度大于0，則進入反射拉伸波傳播子階段。在反射拉伸波傳播子階段，若彈體的速度等于0，則彈體總侵徹深度Dp=h1+h21+h22。

3）經歷了剪切壓縮階段后，若彈體的速度仍大于0，則進入拉伸變形階段。進入拉伸變形階段后，若彈體的速度足夠大，以致于能夠使變形錐達到極限應變狀態，即θv≥θε，則彈體完全穿透層合板，此時彈體的侵徹深度Dp=ht。進入拉伸變形階段后，若彈體的速度不足以使變形錐達到極限應變狀態，即θv＜θε，此時變形錐錐角θ 保持不變，且等于θv，其中θv為

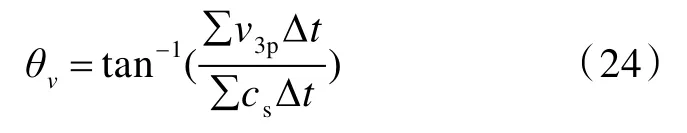
考慮到彈體速度與變形錐角之間存在著相互協調性，則在拉伸變形階段開始的任意時刻都滿足上式，因而有

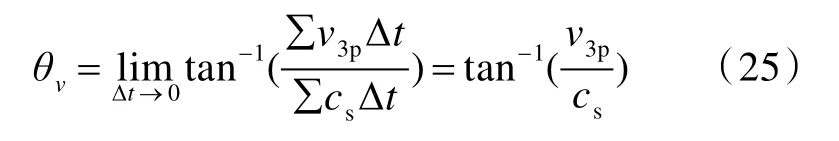
提出上式的理由在于，在變形錐錐角保持為θ=θv的同時，彈體仍具有一定的侵徹能力［13］，從而引起背層未穿透拉伸纖維層的部分失效，即由彈體導致的背層剩余纖維層的部分侵徹。

對拉伸變形階段侵徹深度h3p的計算，則需根據整個侵徹過程的能量守恒方程得到，該方程為

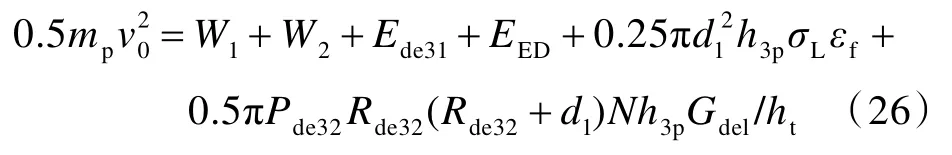
整理后，得到拉伸變形階段彈體部分侵徹的深度h3p為

由此，得到部分侵徹情形下彈體的總侵徹深度Dp為

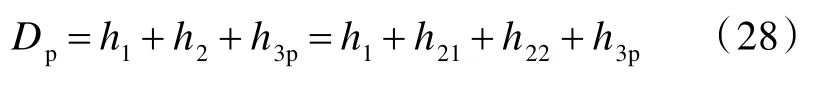
部分侵徹情形下，彈體總侵徹深度的具體計算流程如圖3 所示。

4 層合板彈道極限計算

在對彈體侵徹深度進行計算的基礎上，通過對彈體侵徹深度及彈體速度的判別，可計算層合厚板的彈道極限速度。計算的主要過程如下：

1）設定一個彈體初始沖擊速度值，該速度值小于層合板的彈道極限值。

2）采用上節中的方法計算彈體的侵徹深度，當侵徹深度小于層合板總厚度但彈體速度等于0時，進一步增大彈體初始沖擊速度值并重新計算。

3）繼續增大彈體初始沖擊速度，當彈體的侵徹深度等于層合板總厚度且彈體速度等于0 時，此時彈體的初始沖擊速度即為層合板的彈道極限速度值。

圖4給出了層合厚板彈道極限的計算流程圖。

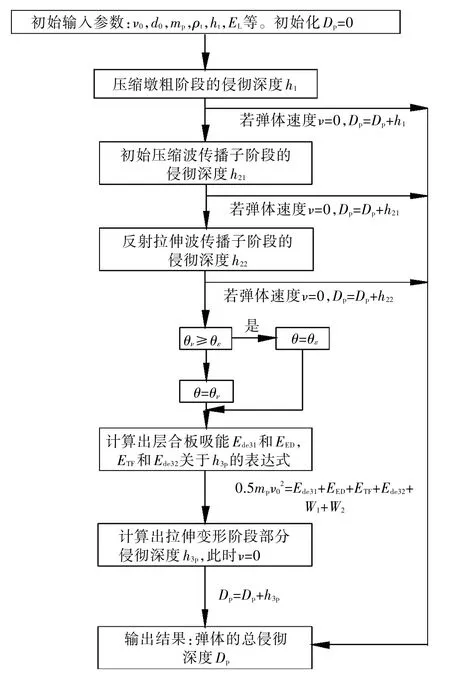
圖3 彈體的侵徹深度（DOP）計算流程圖Fig.3 Flow chart of DOP calculation of projectiles

圖4 層合厚板彈道極限計算流程圖Fig.4 Flow chart of the calculation of ballistic limits for thick laminates

5 試驗驗證及討論

5.1 彈體的侵徹深度比較

為了驗證本文計算模型的實用性和有效性，首先，將未穿透，即部分侵徹情形下彈體的侵徹深度計算值與文獻［5］中的UFRP 層合厚板抗高速侵徹試驗結果進行比較，如表1 所示。表中ht，ρA和v0分別為UFRP 層合板總厚度、面密度和彈體初速。計算過程中UFRP 層合板的材料參數參見文獻［14］。

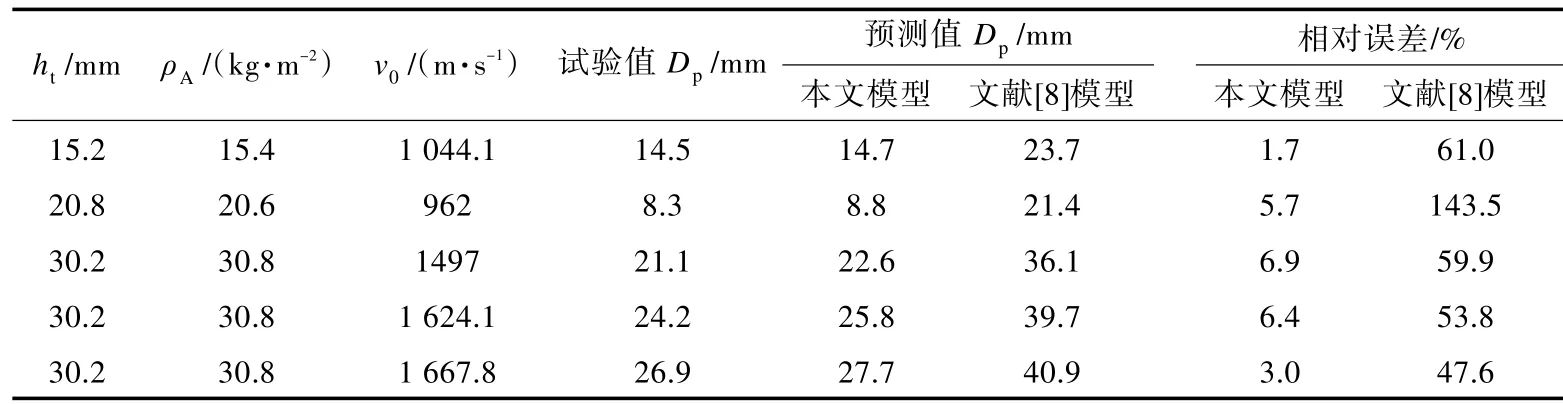
表1 UFRP 層合厚板的侵徹深度（DOP）理論計算值與試驗結果［5］的比較Tab.1 Comparison of DOP between theoretically calculated and experimental［5］results for thick UFRP laminates

由表1 可以看出，采用本文理論模型計算得到的彈體侵徹深度與試驗結果吻合較好。另從表中還可看出，采用本文理論模型計算得到的彈體侵徹深度較試驗值要稍大，這可能與試驗中層合厚板材料性質等的差異，尤其是層間剪切強度的影響有關。另外，在彈體侵徹后期，即進入拉伸變形階段后期，層合板背面未穿透纖維層處于拉剪混合的復雜應力狀態，彈體在侵徹未失效纖維層時，除了會受到纖維層產生的拉伸阻力外，還有可能受到剪切阻力。而本文的理論模型中近似認為只有拉伸阻力作用于彈體，從而導致理論計算模型中彈體的侵徹阻力偏小，進而使得理論計算得到的彈體侵徹深度較試驗結果稍偏大。此外，理論計算中極限變形錐角的取值也可能與實際試驗工況中的極限錐角存在一定的差異，從而影響理論計算的精度。

同時，表1 還給出了采用文獻［8］中理論模型計算得到的UFRP 層合厚板侵徹深度值與試驗結果的比較。由表可知，采用文獻［8］中理論模型計算得到的彈體侵徹深度值和試驗值相比要大得多。這主要是由于文獻［8］的理論模型是建立在局部化破壞模式假定的基礎上，主要針對的是脆性或層間強度較大的層合厚板，其與UFRP 層合厚板抗高速侵徹的破壞機理存在較大差異。尤其是在UFRP 層合厚板拉伸變形階段，對侵徹深度的影響較大，而文獻［8］的理論模型未能很好地考慮到這一點。

5.2 層合板彈道極限比較

進一步采用本文理論模型對層合厚板的彈道極限進行計算，并與文獻［5］中的試驗結果進行比較，如表2 所示。由表2 可知，采用本文理論模型計算得到的層合厚板的彈道極限值與試驗結果吻合較好。另從表2 中還可看出，由本文理論模型計算得到的層合厚板彈道極限值和試驗值相比稍小。這主要是由于在采用本文理論模型計算彈道極限的過程中，是逐步增大彈體速度來使彈體剛好達到臨界穿透（圖1（e）），而此時變形錐處于拉剪混合的復雜應力狀態，變形錐沒有達到極限變形錐角θε即開始出現纖維層失效，致使彈體更容易穿透變形錐后續的纖維層，因而使得彈體穿透變形錐所需的動能偏小，從而導致層合厚板的彈道極限值偏低。

另外，表2 還給出了采用文獻［8］的理論模型計算得到的UFRP 層合厚板的彈道極限值，并與文獻［5］的試驗結果進行了比較。從表中可看出，采用文獻［8］的理論模型計算得到的UFRP 層合厚板彈道極限值較試驗結果低得多。這主要是由2 方面的原因所致：一方面，文獻［8］中的模型并沒有考慮UFRP 層合厚板抗高速侵徹過程中彈體鐓粗變形的影響，使得該模型在整個侵徹過程的計算中層合板的阻抗力被低估，從而導致計算得到的層合板的總吸能偏低；另一方面，文獻［8］中模型不能很好地考慮UFRP 層合厚板拉伸變形效應的影響，致使對UFRP 層合厚板背面纖維層，即拉伸變形階段變形錐纖維層變形和失效的吸能計算偏低。因此，采用文獻［8］中模型計算得到的UFRP 層合厚板的總吸能嚴重偏低，從而導致采用該模型計算得到的UFRP 層合厚板的彈道極限值要遠低于試驗值。

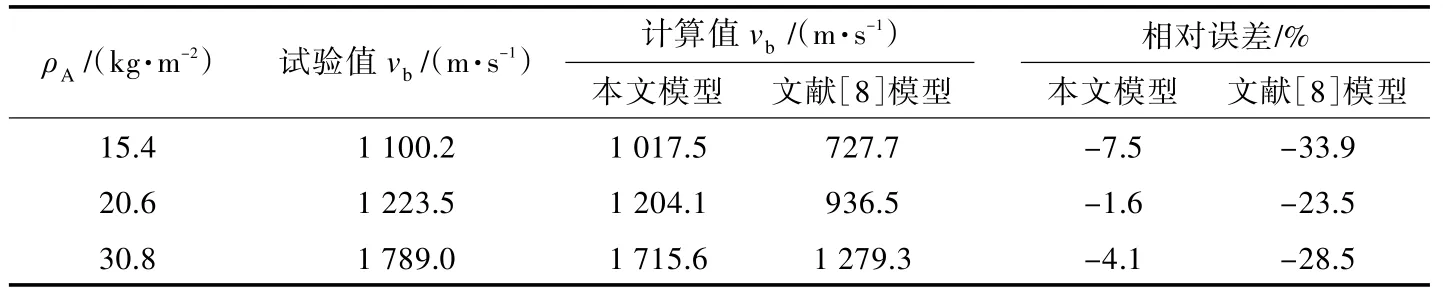
表2 理論計算UFRP 層合厚板彈道極限值與試驗結果［5］的比較Tab.2 Comparison of theoretical and experimental［5］results of ballistic limits for thick UFRP laminates

從上面的對比分析可得出，本文給出的理論計算模型能對UFRP 層合厚板抗高速鈍頭彈侵徹的彈體侵徹深度和層合板彈道極限進行合理且較為準確的預測。不過，應該指出的是，由于彈速及靶板厚度不同，可能會導致侵徹機理出現差異，因而本文模型對速度較低的情形（＜800 m/s）或靶板較薄的情形（ht/d ＜2）誤差可能會較大。

6 結 語

通過對UFRP 層合厚板抗高速侵徹過程的分析，將整個抗侵徹過程分為了開坑鐓粗、剪切壓縮和拉伸變形3 個階段，并基于能量守恒原理建立了UFRP 層合厚板抗高速鈍頭彈侵徹的三階段理論計算模型。利用該模型，對部分侵徹情形下彈體的侵徹深度以及UFRP 層合厚板的彈道極限速度進行了計算，理論計算得到的彈體侵徹深度和層合厚板的彈道極限值均與相應的試驗結果吻合較好，驗證了理論模型的實用性和有效性。而通過與試驗結果的比較表明，本文建立的理論模型能對UFRP 層合厚板抗高速鈍頭彈侵徹的彈體侵徹深度和層合厚板彈道極限進行合理的預測，可以降低試驗成本，具有一定的理論和工程應用價值。

［1］JACOBS M J N，VAN DINGENEN J L J. Ballistic pro?tection mechanisms in personal armour［J］. Journal of Materials Science，2001，36（13）：3137-3142.

［2］梁子青，周慶，邱冠雄，等.超高分子量聚乙烯纖維防彈復合材料的研究［J］. 天津工業大學學報，2003，22（2）：6-9.LIANG Ziqing，ZHOU Qing，QIU Guanxiong，et al.Study on ultra-high molecular weight polyethylene anti?ballistic composites［J］. Journal of Tianjin Polytechnic University，2003，22（2）：6-9.

［3］TAN V B C，KHOO K J L. Perforation of flexible lami?nates by projectiles of different geometry［J］. Interna?tional Journal of Impact Engineering，2005，31（7）：793-810.

［4］顧冰芳，龔烈航，徐國躍.UHMWPE 纖維復合材料防彈機理和性能［J］.纖維復合材料，2006（1）：20-23.GU Bingfang，GONG Liehang，XU Guoyue.Ballistic re?sistance mechanism and performance of UHMWPE composites［J］.Fiber Composites，2006（1）：20-23.

［5］王曉強，朱錫，梅志遠，等.超高分子量聚乙烯纖維增強層合厚板抗彈性能實驗研究［J］. 爆炸與沖擊，2009，29（1）：29-34.WANG Xiaoqiang，ZHU Xi，MEI Zhiyuan，et al. Ballis?tic performances of ultra-high molecular weight poly?ethylene fiber-reinforced thick laminated plates［J］.Explosion and Shock Waves，2009，29（1）：29-34.

［6］王曉強，朱錫，梅志遠.高速鋼質破片侵徹高強聚乙烯纖維增強塑料層合板試驗研究［J］. 兵工學報，2009，30（12）：1574-1578.WANG Xiaoqiang，ZHU Xi，MEI Zhiyuan. An experi?mental research on high velocity steel fragments perfo?rating UHMWPE FRP laminates［J］. Acta Armamenta?rii，2009，30（12）：1574-1578.

［7］WEN H M. Predicting the penetration and perforation of FRP laminates struck normally by projectiles with different nose shapes［J］. Composite Structures，2000，49（3）：321-329.

［8］WEN H M. Penetration and perforation of thick FRP laminates［J］. Composites Science and Technology，2001，61（8）：1163-1172.

［9］覃悅，文鶴鳴，何濤.卵形彈丸撞擊下FRP 層合板的侵徹和穿透［J］. 復合材料學報，2007，24（2）：131-136.QIN Yue，WEN Heming，HE Tao. Penetration and per?foration of FRP laminates under normal impact［J］. Ac?ta Materiae Compositae Sinica，2007，24（2）：131-136.

［10］NAIK N K，SHRIRAO P. Composite structures under ballistic impact［J］. Composite Structures，2004，66（1/4）：579-590.

［11］NAIK N K，SHRIRAO P，REDDY B C K. Ballistic impact behaviour of woven fabric composites：formula?tion［J］. International Journal of Impact Engineering，2006，32（9）：1521-1552.

［12］古興瑾，許希武，黃晶.層合復合材料薄板高速沖擊損傷研究［J］. 南京航空航天大學學報，2008，40（3）：370-375.GU Xingjin，XU Xiwu，HUANG Jing. High velocity impact damage of thin composite laminates［J］. Jour?nal of Nanjing University of Aeronautics and Astro?nautics，2008，40（3）：370-375.

［13］梅志遠，朱錫，張立軍.FRC 層合板抗高速沖擊機理研究［J］.復合材料學報，2006，23（2）：143-149.MEI Zhiyuan，ZHU Xi，ZHANG Lijun. Ballistic pro?tective mechanism of FRC laminates［J］. Acta Materi?ae Compositae Sinica，2006，23（2）：143-149.

［14］陳長海，朱錫，王俊森，等. 高速鈍頭彈侵徹中厚高強聚乙烯纖維增強塑料層合板的機制［J］. 復合材料學報，2013，30（5）：226-235.CHEN Changhai，ZHU Xi，WANG Junsen，et al.Mechanism of high-velocity blunt-nosed projectiles penetrating moderately thick UHMWPE fiber rein?forced plastic laminate［J］. Acta Materiae Compositae Sinica，2013，30（5）：226-235.

［15］張曉晴，楊桂通，黃小清.柱形平頭彈體墩粗變形的理論分析［J］. 華南理工大學學報（自然科學版），2005，33（1）：32-36.ZHANG Xiaoqing，YANG Guitong，HUANG Xiaoq?ing. Theoretical analysis of the mushrooming deforma?tion of flattened cylindrical projectile［J］. Journal of South China University of Technology（Natural Sci?ence Edition），2005，33（1）：32-36.