Design of Ballisric Consisrency Based on Leasr Squares Supporr Vecror Machine and Parricle Swarm Oprimizarion
Zhang Yuchen(張宇宸),Du Zhonghua(杜忠華),Dai Wei(戴煒)
(1.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,P.R.China;2.Armored Vehicle Providing Ground,Beijing 100072,P.R.China)
(Received 25 October 2014;revised 18 July 2015;accepted 14 September 2015)
Design of Ballisric Consisrency Based on Leasr Squares Supporr Vecror Machine and Parricle Swarm Oprimizarion
Zhang Yuchen(張宇宸)1*,Du Zhonghua(杜忠華)1,Dai Wei(戴煒)2
(1.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,P.R.China;2.Armored Vehicle Providing Ground,Beijing 100072,P.R.China)
(Received 25 October 2014;revised 18 July 2015;accepted 14 September 2015)
Absrracr:In order to improve the firing efficiency of projectiles,it is required to use the universal firing table for gun weapon system equipped with a variety of projectiles.Moreover,the foundation of sharing the universal firing table is the ballistic matching for two types of projectiles.Therefore,a method is proposed in the process of designing new type of projectile.The least squares support vector machine is utilized to build the ballistic trajectory model of the original projectile,thus it is viable to compare the two trajectories.Then the particle swarm optimization is applied to find the combination of trajectory parameters which meet the criterion of ballistic matching best. Finally,examples show the proposed method is valid and feasible.
ballistic matching;least squares support vector machine;particle swarm optimization;curve fitting
0 Inrroducrion
Ballistic matching is a characteristic that the ballistic trajectory of different projectiles resemble each other when fired in the same gun.The form factors,projectile mass and muzzle velocities of different kinds of projectiles usually differ from each other.In a certain firing condition,there is the best combination to meet the criterion of ballistic matching.In order to get a better result,the characteristic should be considered as a rule in the process of designing new kind of projectile. Otherwise,it is difficult to satisfy the ballistic matching.Ballistic matching is the foundation of the universal firing table[1].
From the viewpoint of mathematical statistics,the test of the ballistic matching belongs to the mathematical expectation test where the probability error is unknown.Therefore,t-test is utilized in this situation[2].Considering that the ballistic trajectories of the two projectiles are random variables,the firing test should be conducted at a certain amount of samples to obtain the trajectories and the conclusion can be drew whether or not the two projectiles meet the criterion of the ballistic matching through the theory of the mathematical statistics.However,it often reaches a false conclusion due to the dispersion of the firing and the influence of outlier[3].
Considering that it is difficult to test practical firing in the early period of designing new ammunition,theoretical computation is preferred to draw the preliminary conclusion that whether the projectile reaches the criterion of the ballistic matching.
Aiming at gaining the combination of trajectory parameters which matchs the consistency of the track in flight,a series of mathematical models are established and two actual cases are simulated.
1 Numerical Solurion of Ballisric Model
Ignoring the secondary factors such as wind velocity,wind direction,and so on,point-massequations are shown as follows[4]
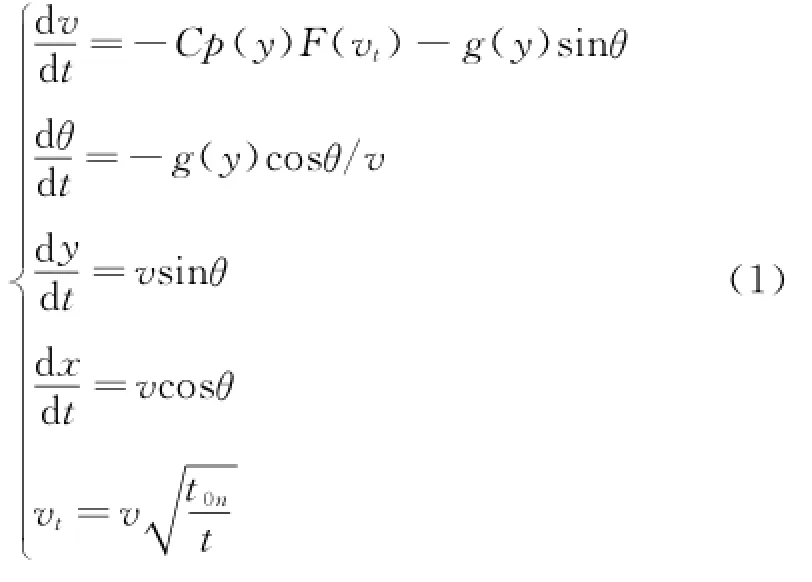
where vtis the modest velocity which is linear with the projectile velocity,t the modest temperature,t0nthe standard value on the ground of the modest temperature,p(y)the air density function at altitude y,F(vt)the dimensional drag function at the modest velocity vt,g(y)the acceleration due to gravity at altitude y,and C the ballistic coefficient which is shown as follows
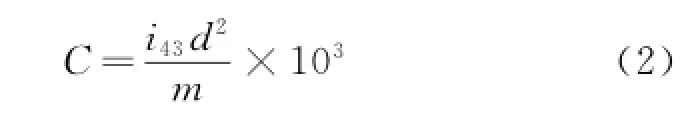
where d is the projectile reference diameter,i43the form factor,and m the projectile mass.
While solving the point-mass equations,initial conditions should be determined as follows.
When t=0,one has

In comparison with the two trajectories,the muzzle velocity v0,the form factor i43,and the projectile mass m are generally different while the projectile diameter d,the angleθ0,and the firing position x0,y0are the same.In general,the muzzle velocity v0,the form factor i43,and the projectile mass m can vary independently when designing a new type of ammunition.Therefore,the situation is discussed in which the three parameters above vary simultaneously.
The point-mass Eq.(1)can be solved precisely with the forth order Runge-Kutta method. However,two sets of points cannot be compared because the displacement of the projectile is usually different at the same time step size.There are several methods to solve the problem.One of them is to express the original trajectory as a function,so the ordinate of the two trajectories can compare each other at the same abscissa.
2 Firring Ballisric Trajecrory wirh LSSVM
In order to fit the curve of ballistic trajectory,several methods have been developed such as the method of least square based on the testing data and linear interpolation based on the ballistic equations.Moreover,artificial neural network[5]and support vector machine were proposed contemporarily.The least squares support vector machine(LSSVM)is introduced to fit the ballistic trajectory[6].
Support vector machine(SVM)which was developed on the basis of statistical learning theory is becoming a hot topic in machine learning field for its theoretical foundation and generalization ability[7].SVMs are particular classifiers which are based on the margin maximization principles.They were based on structural risk minimization,which was introduced to machine learning by Vapnik[8],and had yielded excellent generalization performance.
LSSVM is a variant of the standard SVM.It has been shown by a meticulous empirical study that the generalization performance of LSSVM is comparable to that of SVM.
Least squares support vector regression can be viewed as minimizing the following optimization problem[9]

where J(w,e)is the optimal function,w the normal vector of the hyperplane,e the prediction residual vector,C∈R+,namely the regularization parameter,andφ(·)the mapping from the input space to the feature space.In practice,Eq.(4)is solved by optimizing the Lagrangian,namely
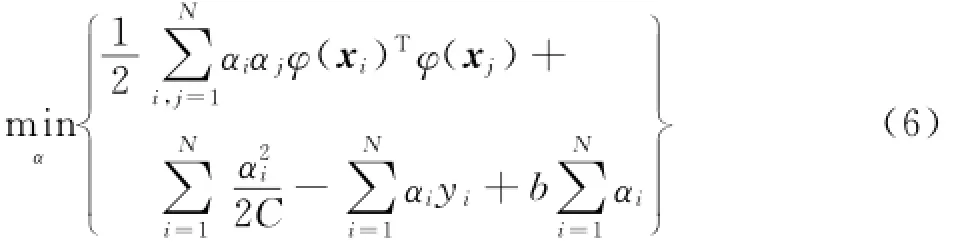
k(·,·)is the kernel function on the paired input to replaceφ(xi)Tφ(xj).The commonly used kernel function is the Gaussian defined
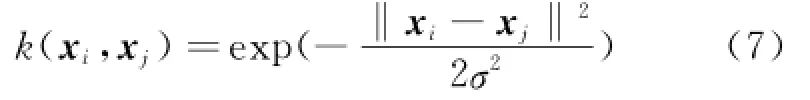
Considering the Lagrangian given by Eq.(6),one has
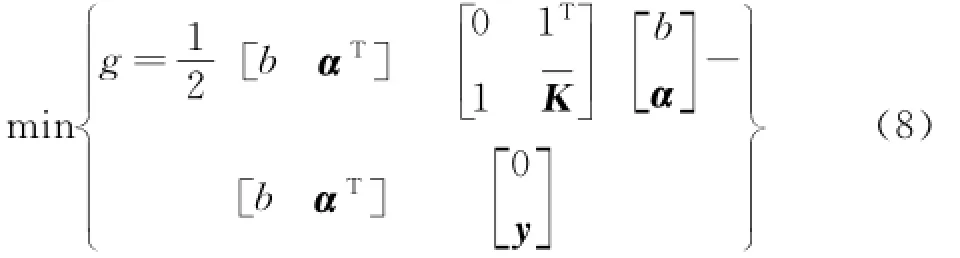
With LSSVM,the relation underlying the data set is represented as a function of the following form
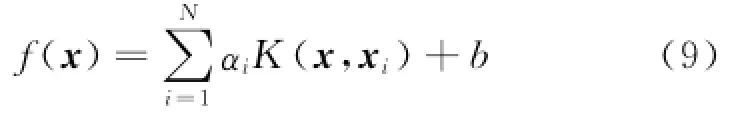
where b andα=[α1,α2,…,αN]Tare obtained from
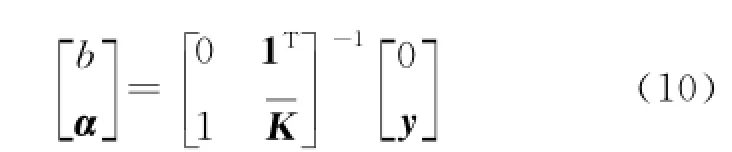
After gaining the function of the original ballistic trajectory,the difference between the ordinate of the two trajectories can be calculated at the same abscissa.According to the difference,the parameters of the ballistic trajectory can be changed to optimize the new type of the projectile.
3 PSO Algorirhm in Oprimizing Ballisric Paramerers
According to the point-mass equations,the ballistic trajectory is determined by four variants which are muzzle velocity,form factor,projectile mass and gun elevation angle[10].The trajectory will differ as long as one or more of the four parameters are modified.In order to find the most optimal solution of ballistic matching between two trajectories,all the above parameters will be taken into account.In addition,the gun elevation angles are the same when in comparison between the two trajectories.Therefore,in this section another three parameters will be the variants of the point-mass equations.
As concluded in Section 1,each variant is independent of another one which is nonlinear with the trajectory.For this nonlinear combination optimization problem,there are various algorithms like genetic algorithms,evolutionary programming etc.In this section,the particle swarm optimization(PSO)algorithm is utilized to solve the problem[11].
The main steps in the particle swarm optimization process are described as follows[12].
Consider solving the generic optimization problem
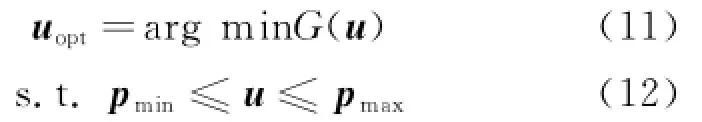
where u=[u1,u2,…,um']Tis the m'-dimensional parameter vector to be optimized and G(·)the optimization function.pmax,pmindefine the search space.
(1)Swarm initialization:Set the iteration index l=0 and randomly generatesearch space.
(2)Swarm evaluation:Each particlean optimization function Gassociated with it.Each particleremembers its best position visited so far,denoted asEvery particle also knows the best position visited so far among the entire swarms,denoted as gb(l).The cognitive information and the social information are updated at each iteration as follows
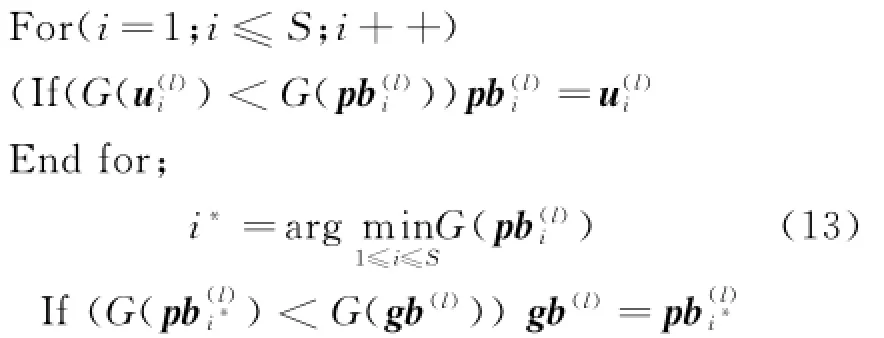
(3)Swarm update:Each particle
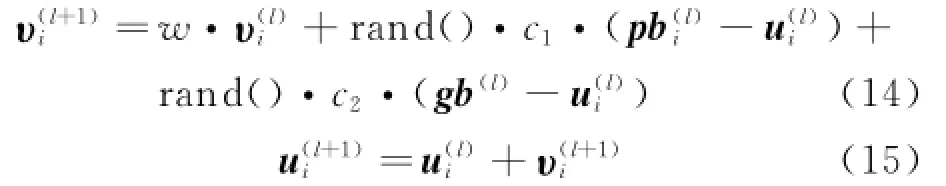
where w is the inertia weight and rand()the uniform random number between 0 and 1.c1and c2are the two acceleration coefficients.
(4)Termination condition check:If the maximum number of iterations,Imax,is reached,terminate the algorithm with the solution gb(Imax);otherwise,set l=l+1 and go to Step(2).
According to the PSO algorithm,the optimization function G(·)can obtain the minimum value by using the global optima solution gb(Imax). In this paper,take mean square error(MSE)between two ballistic ordinate as the optimization function G(u)
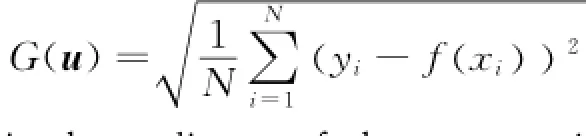
where yiis the ordinate of the new projectile ballistic trajectory and f( xi) the ordinate of the original projectile solved by LSSVM.
MSE is one of the most fundamental techniques of statistical signal processing.It indicates the difference between two trajectories very well. The less MSE of the trajectory ordinate is,the more satisfactorily the new trajectory matches the original one.
4 Examples
Example 1Given by an original projectile,its mass m=18.7 kg,muzzle velocity v0=782 m/s,form factor i43=0.995,muzzle angle thetaθ0= 22 mil(1.32°).The target in ground is 2.5 km far away from the initial location.
Take the point set D={(xi,yi)obtained from the set of the equations of the ballistic trajectory as the training data.With LSSVM,the relation underlying the data set is represented as y=f(x).
Then v0,i43,m consist in the three-dimensional parameter vector to be optimized.With the PSO algorithm,the minimum value can be obtained from the optimization function G(u).The search space is usually given by particular demand.In this example,the search space is given as shown in Table 1.

Table 1 Three-dimenrional search space of Example 1
Through the 20th iterations for 15 particles,the optimal combination is shown as Table 2.

Table 2 Oprimal resulr wirh PSO algorirhm of Example 1
The comparison between the ballistic elements of the original projectile and the new one is shown as Table 3.
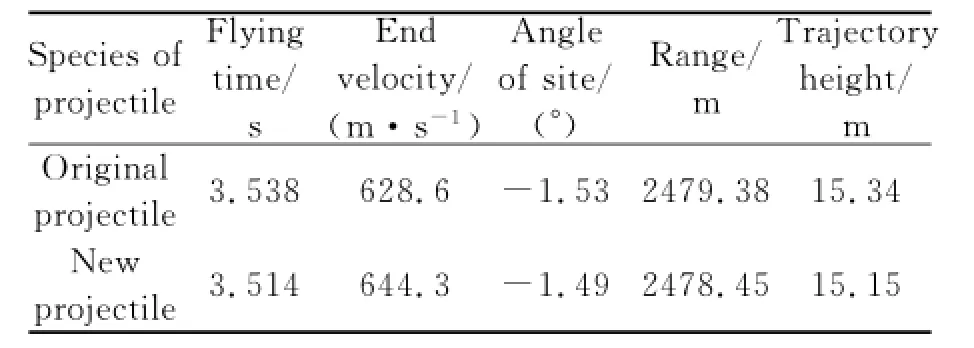
Table 3 Comparison of ballisric paramerers of Example 1
According to the optimistic conclusion,MSE of the trajectory is 0.101,the range of the original trajectory is 0.93 m longer than the new trajectory.As is shown in Fig.1,the two initial trajectories are found to be similar to each other due to the same fire angle.As the velocity of both projectiles decreases,the impact of the gravity increases.Thus,the trajectory starts to differ from each other.The maximal altitude difference of the two trajectories is 0.19 m when the both projectiles reach their maximum altitude.Afterwards,the trajectory descends with the impact of the gravity.Therefore,the two trajectories also almost coincide with each other.As a whole,the two trajectories resemble each other.
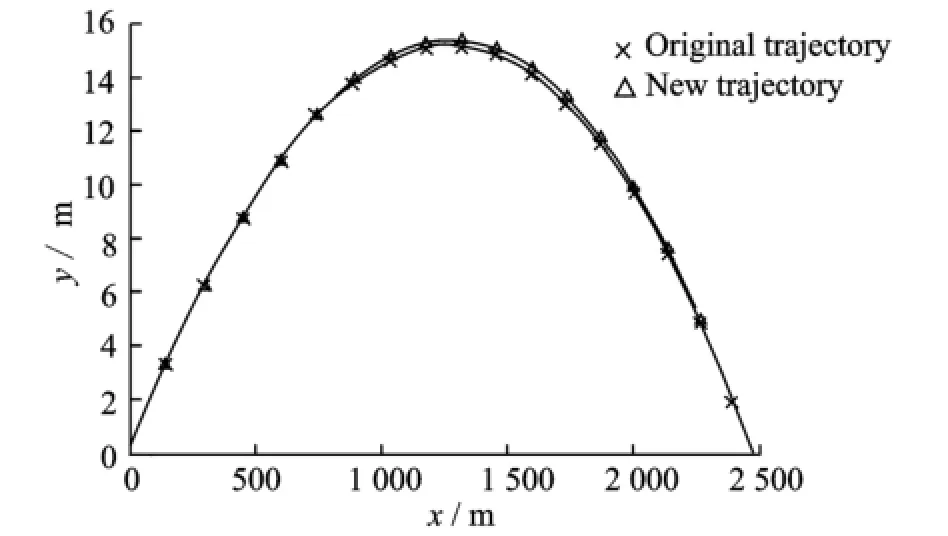
Fig.1 Comparison between two trajectories of Example 1
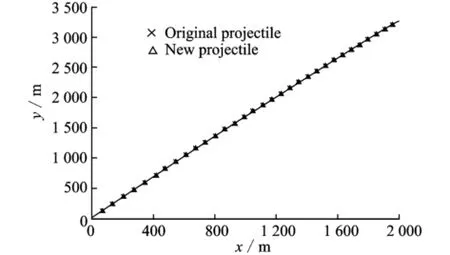
Fig.2 Comparison between two trajectories of Example 2
Example 2Given by an anti-aircraft projectile,its mass m=21.7 kg,muzzle velocity v0= 713 m/s,form factor i43=0.82,muzzle angle θ0=60°.The target in the air is 2 km higher than the initial position.
In Example 2,the search space is given as shown in Table 4.
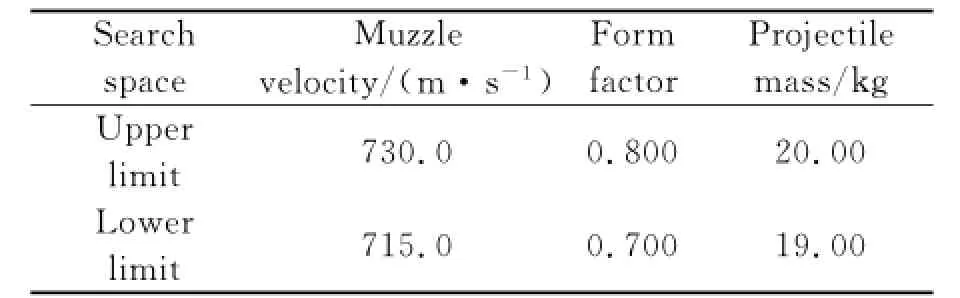
Table 4 Three-dimenrional search space of Example 2
Through the 20th iterations for 15 particles,the optimal combination is shown as Table 5.

Table 5 Oprimal resulr wirh PSO algorirhm of Example 2
The comparison between the ballistic elements of the original projectile and the new one is shown as Table 6.
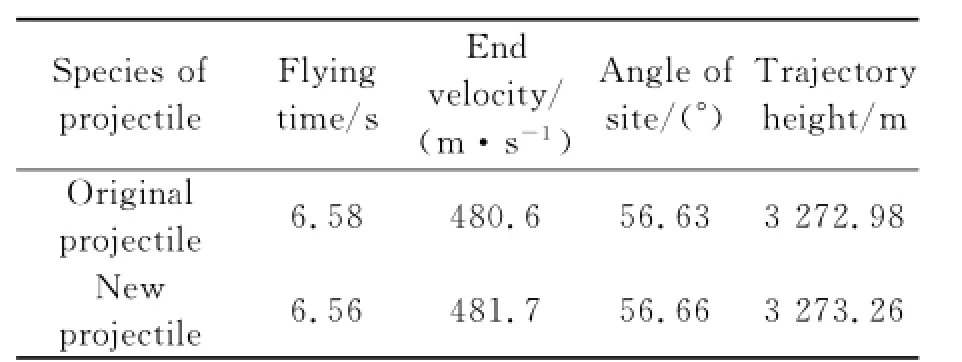
Table 6 Comparison of ballisric paramerers of Example 2
According to the optimistic conclusion,MSE of the two trajectories is 0.53,the trajectory height of the original projectile is 0.28 m lower than the new one as shown in Fig.2.As a whole, the two trajectories resemble each other.
5 Conclusions
A design method for the new type of projectile is discussed to ensure that its trajectory meets the criterion of ballistic matching.Exterior ballistic trajectory is calculated based on the point-mass equation because this equation is a very practical and accurate approximation to the actual trajectory to some extent.With LSSVM,the original trajectory is fitted into a nonlinear function,so the two trajectories can be compared numerically. In order to reach the minimum difference of the two trajectories,the PSO algorithm is introduced to find the optimization combination of projectile parameters.Thus,the conclusion can be drew that weather or not the new type of the projectile can share the same firing table with the original projectile.
Acknowledgemenr
This work was supported by the National Natural Science Foundation of China(No.51006052).
[1] Zhang Lingke,Wang Zhongyuan,Guo Wenjuan. Testing criterion for improving flight trajectory consistence[J].Journal of Gun Launch&Control,2006,1(1):1-5.(in Chinese)
[2] Xu Mingyou.A problem on the examination criterion of trajectory coincidence test[J].Journal of Ballistics,2004,16(1):16-18.(in Chinese)
[3] Guo Xifu,Qian Mingwei,Wang Liangming.Accepting limit in test of the application of firing table for different munitions[J].Journal of Nanjing University of Science and Technology,2003,27(5):478-482.(in Chinese)
[4] Pu Fa.Exterior ballistics[M].Beijing:National Defense Industry Press,1980.(in Chinese)
[5] Bishop C M.Neural networks for pattern recognition[M].Oxford:Oxford University Press,1995.
[6] Han Zipeng.Exterior ballistics of projectiles,rockets and missiles[M].Beijing:Beijing Institute of Technology,2008.(in Chinese)
[7] Suykens J A K,Van Gestel T,De Brabanter J,et al. Least squares support vector machines[M].Singapore:World Scientific,2002.
[8] Suykens J A K,Vandewalle J.Least squares support vector machine classifiers[J].Neural Processing Letters,1999,9(3):293-300.
[9] Suykens J A K,Brabanter J D,Lukas L,et al. Weighted least squares support vector machines:Robustness and sparse approximation[J].Neurocomputing,2002,48(1/2/3/4):85-105.
[10]Zhao Yongping,Sun Jianguo.Fast method for sparse least squares support vector regression machine[J]. Control and Decision,2008,23(12):1347-1352.(in Chinese)
[11]Pu Fa.Discussion about the method of designing and testing ballistic consistency[J].Journal of Ballistics,1993(4):62-65.(in Chinese)
[12]Ji Zhen,Liao Huilian,Wu Qinghua.Algorithm and application of PSO[M].Beijing:Science Press,2008.(in Chinese)
[13]Chen Sheng,Hong Xia,Harris C J.Particle swarm optimization aided orthogonal forward regression for unified data modeling[J].IEEE Transactions on Evolutionary Computation,2010,14(4):477-498.
(Executive Editor:Xu Chengting)
O212.1Documenr code:AArricle ID:1005-1120(2015)05-0549-06
*Corresponding aurhor:Zhang Yuchen,Engineer,E-mail:zyc6857997@126.com.
How ro cire rhis arricle:Zhang Yuchen,Du Zhonghua,Dai Wei.Design of ballistic consistency based on least squares support vector machine and particle swarm optimization[J].Trans.Nanjing U.Aero.Astro.,2015,32(5):549-554.
http://dx.doi.org/10.16356/j.1005-1120.2015.05.549
 Transactions of Nanjing University of Aeronautics and Astronautics2015年5期
Transactions of Nanjing University of Aeronautics and Astronautics2015年5期
- Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Performance of Epoxy-Repaired Corroded Reinforced Concrere Beams
- Merhod for Evaluaring Insranraneous Secror Capaciry
- Influence Predicrions of Conracr Effecrs on Mesh Sriffness of Face Gear Drives wirh Spur Gear
- Solurion ro Beacon Conflicr Based on IEEE 802.15.4
- Topological Srrucrure of US Flighr Nerwork Based on Complex Nerwork Theory
- Average Incremenral Correlarion Analysis Model and Irs Applicarion in Faulr Diagnosis
