一種基于丹麥法的改進型雙步M 估計

林國標 劉立龍 蔡成輝 黎峻宇 黃良珂

1 廣西礦冶與環境科學實驗中心，桂林市建干路12號，541004

2 桂林理工大學測繪地理信息學院，桂林市建干路12號，541004

3 廣西空間信息與測繪重點實驗室，桂林市建干路12號，541004

抗差估計的抗差性及有效性主要取決于初值的準確性與權函數的合理性［1］。目前，一般選取最小二乘估計的結果作為抗差估計的初值［2］，但最小二乘估計對粗差具有均衡性和不敏感性，致使粗差觀測值的殘差并非最大，導致選權迭代時出現錯誤的判斷。同時，合理的權函數應該分3段：正常段、可疑段、淘汰段，其臨界值和均方差因子應根據實際情況選取，具有可變性［1，3］。在傳統的抗差估計方法中，Andrews法、Tukey 法不含正常段，Huber 法、丹麥法沒有淘汰段，IGG法、Hampel法雖然具有正常段、可疑段及淘汰段，但其臨界值往往取某一固定的先驗值。這些方法僅采用一步抗差估計［4］，具有一定的局限性。

針對以上問題，本文提出一種基于丹麥法的改進型雙步M 估計方法。采用抗差性較強的L1－范估計的平差值作為抗差估計的初值，在丹麥法等價權函數的基礎上引入淘汰域，將改進的丹麥法權函數作為抗差權，選取可變動的臨界值，通過雙步M 估計，提高抗差估計的精度。

1 改進型雙步M 估計

1.1 初值選取

由于LS估計不具抗差性，LS估計的殘差不能有效反映粗差的位置。而L1－范估計的平差值具有較好的抗差性，能較為準確地體現真實殘差［5］，本文將其作為雙步M 估計的初值。

首先，列誤差方程：

解得殘差：

然后，以L1－范權函數重新定權，再進行迭代計算，收斂時得殘差初值：

式中，Pi為觀測權，為等價權，V0為初始殘差，l為常數項，c為一個很小的正常數。

1.2 等價權函數選擇

丹麥法的權函數如下［3］：

丹麥法權函數缺乏淘汰段，導致抗差效率降低。加入淘汰段，對丹麥法進行改進：

1.3 第一步——綜合抗差階段

該階段有兩個關鍵問題需要解決：一是確定臨界值k0、k1，二是選取等價權。k0、k1一般分別取某一固定值［3］，k0＝1～2.5，k1＝3～6。臨界值在k0、k1基礎上再乘以一個可變因子（r為多余度），可解決臨界值取值不當的問題，實現系數陣空間與觀測空間的同時抗差［6］。r的平均值為（n－m）／n（n、m分別為觀測值個數與參數個數），故可變因子為。此時臨界值會隨具體問題而變化，增強了抗差估計的靈活性。本文取k0＝2d，k1＝4d。

選取改進后的丹麥法等價權作為抗差權，單位權中誤差σ0采用第一次或第二次抗差估計所求得的觀測殘差來計算，能夠獲得比較準確的均方差因子［7］：

1.4 第二步——優化階段

將第一步所得的估計值作為該階段的初值，利用截尾LS法重新平差計算。取權函數［8］：

臨界值取k＝3。根據此時的v與σ2，將大于3倍均方差的觀測值刪去，然后利用剩余的觀測值進行加權LS 平差，得到最終的參數解。精度評定采用：

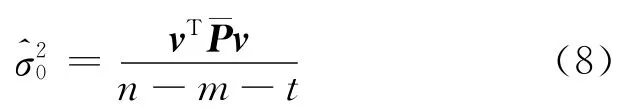
式中，n、m、t分別為總觀測數、必要觀測數和刪去的粗差觀測數；為最終權。

2 算例分析

本文結合一個測邊網算例和一個水準網算例［9］，對比本文提出的改進型雙步M 估計與丹麥法、Huber法、L1法、IGGⅠ法及兩步抗差估計5種方法的平差結果。將無粗差時的LS法平差值當作真值，傳統抗差估計方法和兩步抗差估計的臨界值取先驗值，均方差因子通過初次平差的殘差由中位數法計算，即0.674 5。

算例1 如圖1，測邊網中A、B、C、D為已知點，P1、P2、P3、P4為未知點，觀測13條邊長，測距精度σS＝3mm＋1×10－6S。起算數據及觀測邊長見表1。在第3、12條邊上分別附上－30dm、50 dm 的粗差，各種抗差估計方法的計算結果見表2。

圖1 測邊網圖Fig.1 Trilateration network

算例中，測邊網的污染率為15.4%，屬于較嚴重污染。由表2可知：

1）在參數估計方面，幾種傳統抗差估計方法的估計結果與真值之差較大：丹麥法、Huber法、L1法和IGGⅠ法最大的差值分別為11.2cm、30.4cm、20.3cm、43.1cm；兩步抗差估計的結果與真值之差較小，最大為－3.2cm；本文方法與真值之差較小，最大差值為－2.5cm，整體比兩步抗差估計小一些。

2）在最終權方面，P3、P12為粗差權，其余為正常觀測值的最終權，傳統抗差估計方法的P3、P12未能同時降到最小或0，如丹麥法、Huber法、L1法和IGGⅠ法的P3分別為0.03、0.11、0.03、0.13，L1法正常觀測值的最終權受粗差影響波動很大；兩步抗差估計的P3、P12均降為0，而P6、P8、P13分別降為0.42、0.40、0.73；本文方法的P3、P12均降為0，其余權值均為觀測權。

若在上述粗差基礎上再加上一個粗差，即在第3、10、12條邊上分別附上－30dm、－20dm、50dm 的3個粗差，再一次進行平差計算，則各種抗差估計方法的計算結果見表3。此時測邊網的污染率為23.1%。由表3可知：

表1 測邊網觀測數據及起算數據Tab.1 Observed value and known data

表2 各種抗差估計方法的計算結果Tab.2 Results by various robust estimation methods

表3 各種抗差估計方法的計算結果Tab.3 Results by various robust estimation methods

1）在參數估計方面，傳統抗差估計方法和兩步抗差估計的結果與真值之差比較大，如丹麥法、Huber法、L1法、IGGⅠ法和兩步抗差估計的最大差值分別為109.0、175.6、115.1、121.8、121.8 cm；本文方法的結果與真值之差較小，最大僅為－2.7cm。

2）在最終權方面，P3、P10、P12為粗差權，其余為正常觀測值的最終權。傳統抗差估計方法和兩步抗差估計的P3、P10仍為觀測權，分別為1.86、14.2，L1法的粗差權雖然最后有所降低，但是正常觀測權之比波動很大；本文方法的P3、P10、P12均降為0，其余權仍為觀測權。

綜上所述，當測邊網含有2個粗差時，傳統抗差估計方法的抗差效果較差，兩步抗差估計和本文方法的抗差效果較好，而本文方法的整體抗差效果優于兩步抗差估計；當測邊網含有3個粗差時，傳統抗差估計方法和兩步抗差估計基本喪失了抗差估計的能力，而本文方法的抗差效果依然比較顯著。這是由于傳統抗差估計方法和兩步抗差估計往往采用對粗差具有均衡性的LS法的平差結果作為抗差初值，不能準確反映粗差的位置。而前者臨界值是固定的，不能有效適應實際問題，因此它們抵御多維粗差的效果并不顯著。

算例2 如圖2，水準網中A、B為已知點，HA＝8.016m，HB＝9.016m，點P1、P2、P3為待定點。進行7條水準路線觀測，見表4。在第1、4路線上分別附加－20mm、40mm 的粗差，各種方法的計算結果見表5。

圖2 水準網圖Fig.2 Leveling network

表4 水準網觀測高差值及路線長Tab.4 Observed value and length

表5 各種抗差估計方法的計算結果Tab.5 Results by various robust estimation methods

算例中，多余觀測數為4，污染率為28.6%，屬于比較嚴重的污染，因此本算例只進行包含2個粗差的比較。由表5可知：

1）在參數估計方面，傳統抗差估計方法和兩步抗差估計的估計結果與真值之差較大，丹麥法、Huber法、L1法、IGGⅠ法和兩步抗差估計的最大差值分別為－8.7 mm、－8.0 mm、－6.7 mm、－8.3mm、－8.8mm；本文方法的結果與真值之差較小，最大僅為－0.3mm。

2）在最終權方面，P1、P4為粗差權，其余為正常觀測值的最終權，傳統抗差估計和兩步抗差估計的P1、P4未能同時降為0，如丹麥法、Huber法、IGGⅠ法及兩步抗差估計的P1觀測權均為2.73，L1法的P1為0.21，L1法的P3、P7有所降低；本文方法的P1、P4均降為0，其余最終權維持不變。

和算例1同理，因為傳統抗差估計和兩步抗差估計常常采用不能準確反映粗差位置的LS法平差結果作為抗差初值，前者臨界值是固定的，所以往往不能抵抗多維粗差的干擾。而本方法以L1－范估計結果作為初值，第一步的抗差權采用改進的丹麥法等價權，臨界值可變；第二步采用截尾LS法，取得了較好的估計結果。

3 結 語

基于丹麥法的改進型雙步M 估計是一種以L1－范估計的平差值作為初值、以改進后的丹麥等價權作為綜合抗差階段權因子的抗差估計方法，比較有效地解決了抗差估計初值與臨界值選取不當的問題，提高了抗差估計的精度。算例表明，無論是測邊網平差，還是水準網平差，該方法都能有效抵御多維粗差的干擾，獲得優于傳統抗差估計和兩步抗差估計的平差結果，具有較強的抗差性。

［1］楊元喜，吳富梅.臨界值可變的抗差估計等價權函數［J］.測繪科學技術學報，2006（5）：320－324（Yang Yuanxi，Wu Fumei.Modified Equivalent Weight Function with Variable Criterion for Robust Estimation［J］.Journal of Geomatics Science and Technology，2006，（5）：320－324）

［2］邱衛寧.具有穩健初值的選權迭代法［J］.武漢大學學報：信息科學版，2003（4）：452－454（Qiu Weining.Method for Selecting Weight Iteration with Robust Initial Value［J］.Geomatics and Information Science of Wuhan University，2003，（4）：452－454）

［3］李浩軍，唐詩華，黃杰.經典選權迭代法研究與兩步抗差估計的提出［J］.海洋測繪，2007（1）：17－20（Li Haojun，Tang Shihua，Huang Jie.The Discussion about Some Kinds of Selecting Weight Iteration Method［J］.Hydrographic Surveying and Charting，2007（1）：17－20）

［4］靳奉祥.抗差估計理論與方法研究［J］.山東科技大學學報：自然科學版，2003（4）：1－6（Jin Fengxiang.Study on Robust Estimation Theory and Method［J］.Journal of Shandong University of Science and Technology：Natural Science，2003（4）：1－6）

［5］王振杰，歐吉坤，曲國慶.抗差估計的初值選擇［J］.地殼形變與地震，2001（3）：32－35（Wang Zhenjie，Ou Jikun，Qu Guoqing.Choice of Initial Value for Robust Estimation［J］.Crustal Deformation and Earthquake，2001，（3）：32－35）

［6］歐吉坤.一種三步抗差方案的設計［J］.測繪學報，1996（3）：173－179（Ou Jikun.Design of a New Scheme of Robust Estimation by Three Steps［J］.Acta Geodaetica et Cartographica Sinica，1996（3）：173－179）

［7］高曉，戴吾蛟.抗差Helmert方差分量估計在GPS／BDS組合定位中的應用［J］.大地測量與地球動力學，2014，34（1）：173－176（Gao Xiao，Dai Wujiao.Application of Robusthelmert Variance Component Estimation to Position in Combination of GPS and BDS［J］.Journal of Geodesy and Geodynamics，2014，34（1）：173－176）

［8］王福麗，成英燕，韋鋮，等.利用抗差多項式擬合法探測修復GNSS周跳［J］.大地測量與地球動力學，2013，33（3）：129－132（Wang Fuli，Cheng Yingyan，Wei Cheng，et al.GNSS Cycle Slip Detection and Correction Using Robust Polynomial Fitting［J］.Journal of Geodesy and Geodynamics，2013，33（3）：129－132）

［9］武漢大學測繪學院測量平差學科組.誤差理論與測量平差基礎［M］.武漢：武漢大學出版社，2009（Research Group of Surveying Adjustment in School of Geodesy and Geomatics of Wuhan University.Error Theory and Fundation of Surveying Adjustment［M］.Wuhan：Wuhan University Press，2009）