一種基于大數據的前兆異常識別方法——以云南魯甸地震為例

王秀英 張聰聰 楊德賀

1 中國地震局地殼應力研究所，北京市安寧莊路1號，100085

傳統的前兆數據分析方法在實際使用中存在局限性，尤其是觀測數據精度和采樣率大幅提高后，這種局限性愈發突出。這是因為，采樣精度和頻率的提高導致數據量激增，使數據呈現的形態和變化更趨復雜多樣。高頻高精度數據中攜帶了更多低頻數據所不具有的信息，同時也帶來了更多干擾和影響。觀測數據量的變化引發了對數據分析方法改變的需求，大數據分析方法正是基于這樣一種需求應運而生。大數據分析方法目前在互聯網和信息行業得到快速發展和應用，其價值和應用思想也正在被更多行業接納和引入，將大數據的研究思路應用于科學研究也是目前的發展趨勢，并在多個科學研究領域得到應用［1－2］。

地震前兆觀測經過多年發展，目前已形成一個覆蓋全國的數字化、網絡化、智能化的觀測網絡體系。觀測產出數據量巨大，依靠人工分析很難勝任，迫切需要引入新的研究方法。因此，本文嘗試將大數據的研究思想引入前兆數據異常識別分析中。通過對2014－08－03云南魯甸6.5級及該區域之前幾個地震與多測項地震前兆數據聯合應用的相關性探索，展示前兆數據大數據應用的一種思路。

1 數據及方法

1.1 研究數據

觀測數據取自“十五”前兆數據庫，選擇魯甸地震震中周圍150km 范圍內的前兆數據，共有5個臺站24個測項分量數據參與計算。參與計算的測項分量如表1所示。

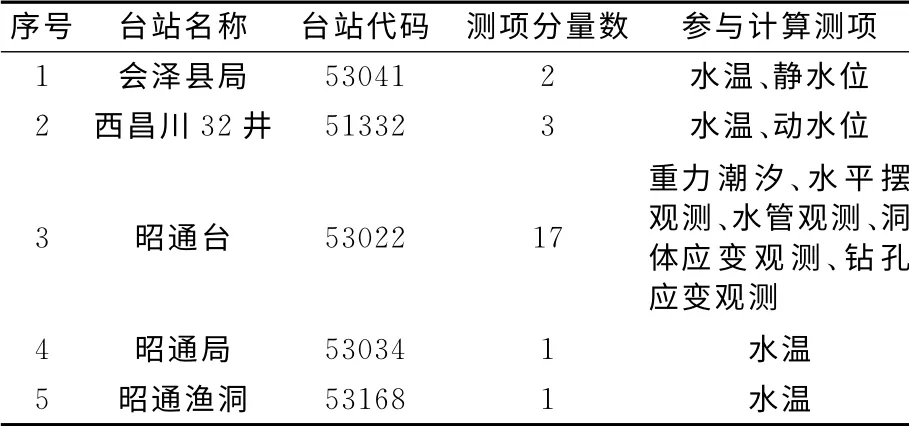
表1 臺站測項分量及測項數量Tab.1 Observation item and total items of each station

自2013年以來，除本次魯甸地震和2014－04－05地震，研究區附近沒有其他較大地震。因此，先選取這些測項分量2013－01－01～2014－08－02的時均值數據作為研究對象，進行魯甸地震的前兆數據異常識別；之后，利用該區域更長時段的數據，進行更多實例的驗證。

1.2 研究方法

傳統前兆數據分析方法都是針對單一測項的分析模式，異常識別靠人工觀察，在識別為異常后需逐一排除干擾和影響，才能進行異常分析。針對較多測項、較長時間的觀測數據進行分析時，單測項逐一分析的方式顯然不可行。因此，需要利用算法自動檢測并識別異常。

本文所用的異常識別算法是結合前兆觀測數據特點研制的，主要檢測原理是：將前兆觀測數據作為一個時間序列，利用搜索算法找到時間序列的關鍵點，再用關鍵點將時間序列劃分為若干子序列，以子序列的長度、高度、均值、方差作為子序列的模式，利用搜索算法選出其中明顯偏離其他模式的子模式，將其作為一個異常情況。由于前兆數據是按日保存的，單純利用一日的數據可能存在不同日數據銜接部位異常情況的丟失。因此，實際計算時可以將幾個月的數據作為一個大的時間序列，然后采用向前滑動的方式，將計算窗口隨時間逐步推進，最終得到檢測時段的異常檢測結果。本文計算中采用6個月時長作為檢測窗長，3個月時長作為滑動步長。

本文所用的算法可以檢測數據序列中各種異于正常的形態變化，所以各種情況引起的數據異常波動形態都會被檢測出，有時可能一個序列會檢測出多個異常。有關該異常檢測算法的詳細說明，請參閱文獻［3］，這里不再重復。

2 計算結果

利用異常識別算法對24個測項分量自2013年以來的時均值數據作自動掃描檢測，得到異常檢測結果。計算過程中會遇到個別測項個別觀測日連續缺數較多的情況，這時應舍棄該日數據，然后分別對單測項異常檢測和多測項聯合應用的異常檢測結果按自然月進行累計統計。對多個測項逐一累計統計的結果顯示了很強的隨機性，這里不再討論這種情況。但當將多個測項的檢測結果進行綜合累計時，則表現了一些規律性。圖1為按照自然月將全部測項的檢測結果以異常天數、異常次數累計的統計結果。這里異常天數累積的方法為：如果某日數據中檢測出異常情況，則該日累積，沒有異常情況則該日不累積；異常次數的累積方法為將異常檢測結果中檢測的異常數據個數直接累積，如果某日有多個異常數據，則對多個異常數據進行累計。這里統計兩個量的目的是便于比較，當兩個量同時增加時，表明異常時間和異常數量都在增加，對應事件（如地震）的可能性增加；僅有一個量增加時，有可能是干擾因素造成的，還需更進一步分析。

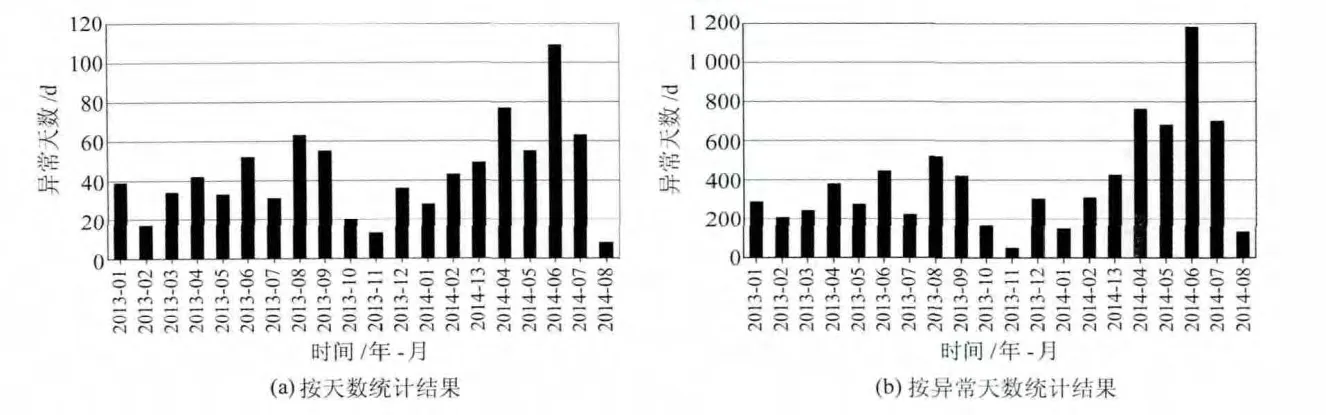
圖1 全部測項按自然月累計統計結果Fig.1 Statistical results of all observation items based on monthly calculation

從圖1中可以看到，無論是按異常天數，還是按異常個數的累計統計結果，在2013－01～2014－03之間表現得比較隨機，而2014－04 后，統計結果較之前有了明顯增加，而且比較集中。2014－08，由于參加統計的只有兩天的數據，在圖上表現得并不明顯。

實際上，由于連續多個數據缺失導致當日數據被舍棄的原因，每個月每個測項參與計算的實際數據天數會有差異。為消除這種差異，將統計結果按參與計算的天數和參與計算的測項數進行平均，所得結果稱之為異常比。具體做法為：首先，計算某個測項在統計時段的異常數據點數，將統計結果除以參與統計的天數，如果沒有缺數，統計天數即為統計時長，但實際中缺數現象非常普遍，通過參與計算數據天數的平均可消除每個統計時段天數不一致帶來的影響。其次，匯總不同測項的累積平均異常數據，將統計結果除以參與統計的測項數。由于斷數、停測、增加新測項等原因，會出現不同統計時段中參與統計的測項個數有差異的情況，通過對測項的平均可消除不同統計時段中測項數量不同帶來的影響。

采用異常比這種方式主要是考慮前兆數據在實際使用中，缺數、斷數、變更觀測等情況比較普遍，如果僅采用有連續觀測的數據，可能實際能參與計算的數據寥寥無幾。大數據應用的基本思路是允許數據的混雜性，基于這種思想，計算中允許數據缺失、不連續，有數據的片段就可以參與運算。

將圖1中兩種統計結果消除這種影響后的統計結果如圖2所示。

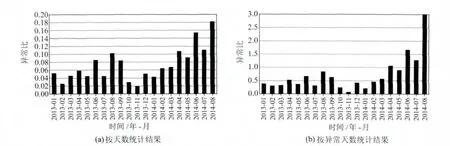
圖2 全部測項按自然月累計的異常比統計結果Fig.2 Ratio statistical results of all items based monthly calculation

從圖2可以看出，按異常比取值后的統計結果中，2014－04后異常突出的情況更加明顯，尤其是2014－08，雖然只有兩天的數據參與計算，利用比例關系會看到非常明顯的異常情況。2014－04魯甸地震之前本區發生一次5級以上地震，圖2中2014－04的統計結果中可能包含了這次地震的影響，也可能隱含了魯甸6.5級的影響，這里不作過多的糾結。2014－05 雖然異常水平稍有降低，但之后的6、7兩月異常水平明顯提高。這種情況至少具有一定的提示或警示意義。

單從圖2的統計結果，似乎看到了一些規律性的東西，這種現象是巧合，還是真的具有相關性，需要進一步驗證。對2013年之前更長時段的數據展開計算分析，將時間追溯至2008－01－01，由于有些臺站2008年初尚未處于運行穩定期，數據質量不太好，因此只以表1中比較集中的1、3、4號臺站數據作為計算對象。

另外，由于前述統計中，針對魯甸地震只統計了地震當月2d的數據，有可能會產生局部放大的效應，所以對更長時段的數據計算及統計結果中分別利用自然月和震前1月（30d）的數據再進行計算比較。2008－01－01～2014－08－02在參與計算的幾個臺站周圍有2次4級地震、3次5級以上地震（包含本次魯甸地震）。表2中給出了以不同時段統計的異常比的結果，及其與地震的對應關系。

表2 地震與異常比對應關系統計Tab.2 Statistical data of earthquakes and their corresponding abnormal ratio

從表2可以看到，隨著時間推移，異常比的均值和方差大致保持相似，符合平穩隨機序列的特征，所以按一定時段統計得到的異常比序列可以看作一個平穩隨機序列，也即長時段的異常比序列大致穩定于一定的水平，可以看作一個背景參考值，當異常比明顯超過背景水平時值得關注。

表2中列出了5個地震按自然月和震前1月（30d）得到的異常比統計結果。按震前當月數據的統計結果，2014－08－03 M6.5地震的異常比超過了3倍均方差的檢測標準；另2次5級以上地震的異常比也都接近2 倍均方差的檢測標準；2次4級以上地震的異常比都小于均值，沒有明顯變化。為和其他按自然月統計標準一致，按震前1月的數據統計異常比，3次5級以上地震的異常比均超過1倍均方差標準，2次4級以上地震的異常比變化不明顯。由此可見，對于研究時段的數據，當按同樣統計時段檢測時，5級以上地震會有比較明顯的異常比變化；震級越大，異常比變化表現得越明顯。另外，對于異常比有明顯變化而無地震的 情 況 統 計，只 有2010－01 和2010－03 兩次。

僅就研究時段得到的結果而言，異常比統計結果與地震之間具有一定的相關性，且震級越大，這種相關性表現越明顯。本文僅進行了按月的統計，也可以采用半月、周等其他時段長度進行統計分析，可能會發現更好的規律。因為由經驗可知，震級越大，越早出現異常，影響范圍越大；震級越小，越晚出現異常，影響范圍越小。不同震級的地震，異常出現的時間和影響范圍，需要通過不同的條件組合，才能發現對異常反應最為突出的情況。這部分內容還需要展開更多計算和分析工作，會在后續的文章中介紹。

本文發現的這種相關性是否普遍存在，目前無法給出確定結論，只有通過對更多數據和震例數據的計算統計，才能確定這種相關性的大小。如果能確定這種相關性的存在，而且相關性較高，可以利用這種方法對數據進行日常監控，發現有持續的異常情況時發出預警，為分析預報、前兆臺網提供輔助信息。有關這方面的研究應用，還需展開更多工作。

3 方法原理分析

對本文呈現的規律性及方法設計依據的初步分析如下。

單個測項由于觀測中會受到各種因素影響，有些因素只影響個別測項或小區域范圍的測項，有些因素則可能會影響多個測項或大區域范圍內的測項。把影響個別測項的因素定義為偶然影響因素，而把同時影響較多測項的因素定義為系統影響因素。偶然影響因素包括諸如電源影響、外界干擾、人為干擾、儀器自身因素等，它們引起的數據異常，從單測項時間軸分布上來看，具有隨機性。系統性影響因素包括地震、地球物理場大的變化、其他大的事件等，它們引起的數據異常，從單測項時間軸分布來看，也是隨機的。這樣，針對單測項數據的分析研究，對數據的精度和連續性具有極高的要求，需要精確定位和分析事件，最終的影響因素可能仍難確定。

有必要將盡可能多的測項數據引入研究中，如本文的計算方法，將盡量多測項的異常進行疊加。這是因為，偶然因素引起的異常，在數量、位置、時間等方面都是隨機的，疊加后仍然是偶然的或隨機的。前文中多測項累計統計數據符合平穩隨機數據序列的特征，這些隨機事件累加的結果會形成一定的背景水平。而系統因素引起的異常，由于同時會影響到很多測項，將它們累計時，即使存在隨機異常背景，仍可以得到疊加放大，從而被突出反映。

對單個測項進行精細分析時，需要逐個事件落實。由于影響因素較多，很難進行準確原因的追溯。但當模糊化處理具體測項的具體異常事件，同時也模糊化時間尺度時，反而會使某些真正的系統性影響因素得以突出，并且很容易識別。

4 結果討論

作為前兆數據利用大數據思想進行研究的一次嘗試，本文僅使用了一種非常簡單的異常檢測算法。無論是地震還是其他因素導致的異常在形態上都表現得多種多樣，需要不同方法的配合，才能比較全面地檢測出各種情況引起的異常。所以，真正的應用，還需結合前兆數據和異常種類的特點研究更多的異常檢測方法，通過多種方法的配合，可以互相印證，或者至少可以加強某種認識，對前兆數據的分析應用也是非常有益的。

需要特別指出，本文選取的臺站和數據是在地震發生后，由地震的位置選取臺站，而真正的數據應用，事先并不知道哪里發生地震，不可能針對具體某幾個臺站展開運算，而應將全部臺站都作為研究對象，通過計算逐步篩選，計算篩選方法還需要大量的研究和實證工作。通過計算逐步篩選，最終確定或鎖定某些臺站對系統性事件的貢獻最大。確定參與計算的臺站需要對大量臺站的大量數據進行梳理分析，與目前單測項數據分析方法截然不同，更多的工作將轉向大數據計算和從海量計算結果中尋求規律的研究。由本文的分析過程可以看到，無論按哪種分類結果進行統計，都需要相當數量的測項參與，才會呈現出一定的規律性；對單個測項的統計結果，規律都不明顯。而這正是大數據分析的核心思想，當更多的數據融合使用時，某些規律不是被淹沒，而是更加明晰。

對單測項數據的精細分析和對更多測項綜合分析的對比，使我們對舍恩伯格在《大數據時代》［2］中的論述理解得更加透徹：小數據使我們的視野局限在可以分析和確定的方面，導致對世界的整體理解可能產生偏差和錯誤，而大數據則可以使我們從不同角度更細致地觀察和研究數據的方方面面。與局限在小數據范圍相比，使用所有數據帶來了更高的精確性，可以讓我們看到一些以前無法發現的細節，更清楚地看到少量樣本數據無法揭示的細節信息。

最后還需要指出的是，雖然在本文中，魯甸地震及另外幾個地震震前異常比累計統計結果有較為明顯的增加，看似異常與地震有很好的對應關系，但由于震例數據較少，不能確定這種相關性是普適的。這種相關性是否存在，或者相關性的大小是多少，還需要對更多震例和數據展開研究，才能給出確定性結論。本文的研究過程，是將地震監測數據與大數據應用思想結合的一次嘗試，具有一定的積極意義，是對傳統數據分析方法的補充和完善。

［1］Hey T，Tansley S，Tolle K.The Fourth Paradigm：Data－Intensive Scientific Discovery［J］.Communications in Computer ＆Information Science，2009，317（8）：1－1

［2］Mayer－Schonberger V，Cukier K.大數據時代：生活、工作與思維的大變革［M］.杭州：浙江人民出版社，2012（Mayer－Schonberger V，Cukier K.Big Data：A Revolution That Will Transform How We Live，Work，and Think［M］.Hangzhou：Zhejiang People’s Publishing House，2012）

［3］張聰聰，王秀英.前兆觀測異常數據檢測方法研究［J］.震災防御技術，2014（9）：615－621（Zhang Congcong，Wang Xiuying.Study on the Detecting Method of Abnormal Earthquake Precursor Observation Data［J］.Technology for Earthquake Disaster Prevention，2014（9）：615－621）