基于排隊(duì)論的公交停靠站通行能力模型研究

尹雨絲，吳 中

(河海大學(xué) 土木與交通學(xué)院，江蘇 南京 210098)＊

0 引言

隨著城市交通擁堵問(wèn)題的日益嚴(yán)重，優(yōu)先發(fā)展公共交通系統(tǒng)是解決我國(guó)交通擁堵問(wèn)題的主要措施.公交停靠站是公共交通系統(tǒng)的重要組成部分，用于公交車輛停靠和乘客上下車.停靠站的有效利用是促進(jìn)公交優(yōu)先的措施之一，對(duì)于解決交通問(wèn)題有重要意義.雖然美國(guó)通行能力手冊(cè)［1］已經(jīng)提供了估算公交停靠站通行能力的公式和圖標(biāo)，但有研究表明其并不準(zhǔn)確［2］.目前大多數(shù)研究基于計(jì)算機(jī)仿真［3-5］，現(xiàn)有的分析模型只適用于入口排隊(duì)始終存在的停靠站［6］，缺乏對(duì)其他實(shí)際情況的分析.因此，有必要對(duì)公交停靠站的通行能力進(jìn)行更切實(shí)際的研究.本文從這一方面入手，在保持目標(biāo)服務(wù)水平的前提下，推導(dǎo)更加適合預(yù)測(cè)公交停靠站最大通行能力的理論模型.該模型以平均車輛延誤作為評(píng)價(jià)指標(biāo)，用“允許公交流量”描述停靠站最大通行能力，強(qiáng)調(diào)服務(wù)對(duì)象的制約作用.

1 研究方法

排隊(duì)論涉及服務(wù)系統(tǒng)的研究主要分為并行系統(tǒng)和串行系統(tǒng)兩類.本文模型以馬爾可夫鏈［7］嵌入在公交車排隊(duì)過(guò)程中為特征，假設(shè)公交停靠站不受交通信號(hào)和其他公交停靠站影響;為多條線路提供服務(wù);公交車的到達(dá)符合泊松分布，在入口排隊(duì)和多泊位停靠站內(nèi)部禁止汽車超車;停靠站用于上下客的公交車服務(wù)時(shí)間服從獨(dú)立同分布［8-9］.

為簡(jiǎn)便起見(jiàn)，本文研究了兩種特殊情況下的精確解.即:①公交車服務(wù)時(shí)間確定的多泊位停靠站;②服務(wù)時(shí)間呈均勻分布的兩泊位停靠站.分別命名為M/D/c串行系統(tǒng)和M/G/2串行系統(tǒng)，以Kendall［10］和SERIAL作為停靠站排隊(duì)規(guī)則.

1.1 嵌入式馬爾可夫鏈

本文定義公交站臺(tái)沒(méi)有公交車停靠的瞬間為一個(gè)再生點(diǎn)，兩個(gè)連續(xù)的再生點(diǎn)之間的時(shí)間間隔為一個(gè)周期.設(shè)?Ln為第n個(gè)周期開(kāi)始時(shí)停靠站入口公交車排隊(duì)數(shù)量;τ為公交車到達(dá)率;c為串行泊位數(shù).可以得到以下結(jié)論:給定τ、c和服務(wù)時(shí)間分布形式，隨機(jī)過(guò)程{?Ln}即為馬爾可夫鏈.

1.2 轉(zhuǎn)移概率

規(guī)定單個(gè)泊位的理論服務(wù)能力μ為1，服務(wù)強(qiáng)度γ=τ/μ=τ.馬爾可夫鏈的轉(zhuǎn)移概率:

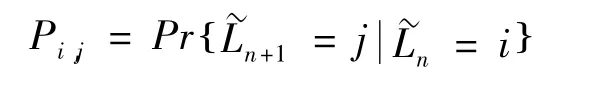
一般情況下，對(duì)任意c和公交車服務(wù)時(shí)間分布，Pi，j可進(jìn)行數(shù)值計(jì)算.對(duì)于M/D/c串行和M/G/2串行系統(tǒng)，Pi，j可以用γ、c和公交服務(wù)時(shí)間的累積分布函數(shù)Fs(t)表示.

1.3 極限概率平衡方程及其求解

令 P=［Pi，j，i≥ 0，j≥ 0］為轉(zhuǎn)移概率矩陣;πi(i≥0)為i狀態(tài)下馬爾可夫鏈的極限概率，即:πi={=i};π=［π1，π2，…］為馬爾可夫鏈的極限分布.因此，π是極限概率平衡方程π=πP的解.

1.4 平均車輛延誤

以平均車輛延誤作為服務(wù)水平評(píng)價(jià)指標(biāo)［11］.令 μ為1是兩個(gè)無(wú)量綱平均延誤的總和:平均等待延誤和平均駐站延誤

若已知c，則TLn和Rn只取決于、和周期內(nèi)服務(wù)的公交車數(shù)Bn.因此:

上述公式適用于M/D/c串行系統(tǒng).由于服務(wù)時(shí)間是確定的，平均駐站延誤在這種情況下是0.M/G/2串行系統(tǒng)的可以用類似的方法獲得，具體步驟在此不再闡述.

2 公交停靠站通行能力的理論模型

2.1 模型建立

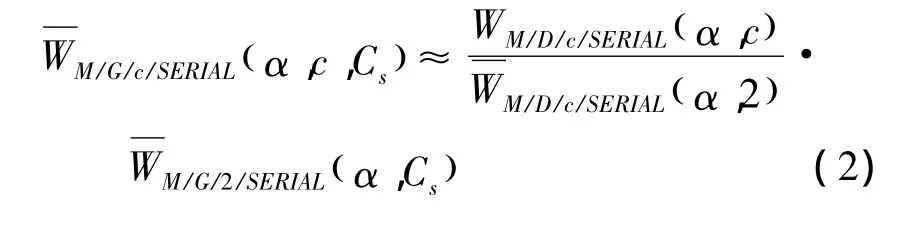
鑒于上述情況，M/G/c串行系統(tǒng)的近似公式可以用排隊(duì)論構(gòu)造［12］:表示排隊(duì)中的平均車輛延誤，服務(wù)率α是公交車流入量與停靠站允許公交流量的最小上界之比.因此，α的取值范圍從0到1.

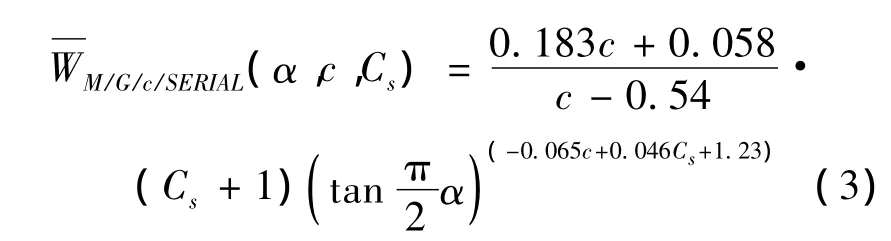
給定

合并(3)、(4)得:W，可以利用負(fù)載率γ 和α 之間的關(guān)系估計(jì)停靠站容許車流量. 即:

2.2 模型驗(yàn)證

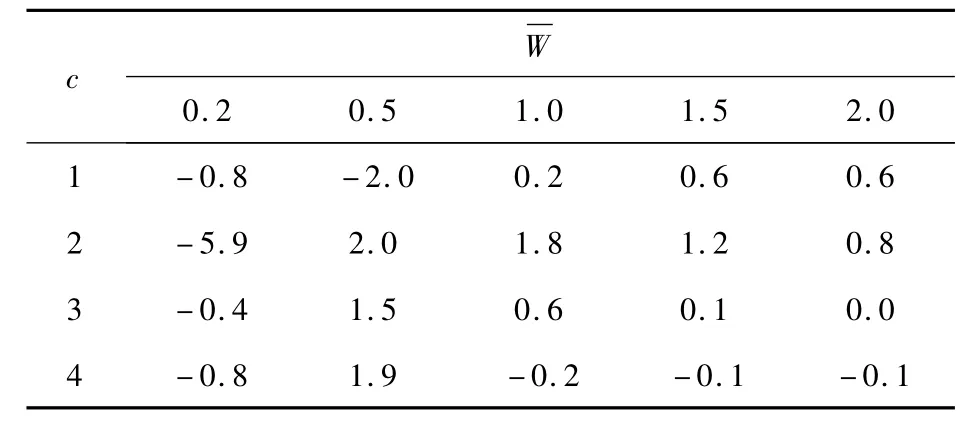
表1 服務(wù)時(shí)間確定的相對(duì)誤差 %

表1給出的是公交車服務(wù)時(shí)間確定時(shí)的結(jié)果，表中的每個(gè)數(shù)據(jù)表示通過(guò)式(7)求得的允許公交流量γ與仿真模擬所得的γ之間的誤差百分比.大多數(shù)情況下誤差在2%以內(nèi)，只有當(dāng)和c很小時(shí)，才會(huì)出現(xiàn)較大誤差.因?yàn)楫?dāng)預(yù)測(cè)值γ本身很小時(shí)，其具有最小平方誤差.

表2 服務(wù)時(shí)間均勻分布的相對(duì)誤差 %

表2給出的是服務(wù)時(shí)間均勻分布時(shí)的結(jié)果.時(shí)間分布的范圍是 [ Smin，Smax]，Smin=1-Cs，Smax=1+Cs.CS的取值范圍由實(shí)際觀察獲到［13］.大多數(shù)情況下誤差在10%以內(nèi)，只有當(dāng)c=1、很小時(shí)，才會(huì)出現(xiàn)較大誤差.較大的誤差可以歸因于式(7)存在最小平方誤差.

3 模型的效應(yīng)分析

3.1 最大泊位通行能力

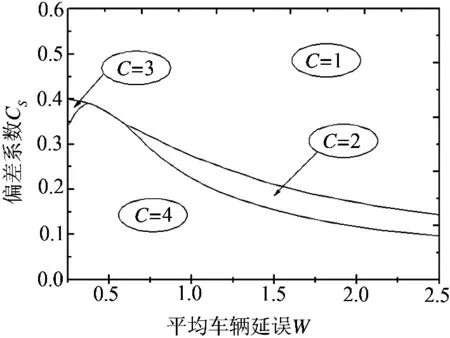
圖1 c泊位停靠站最大單泊位允許交通流量

3.2 公交車擁堵

將多泊位停靠站的允許公交流量γ與理想停靠站(公交車可以自由超越停駐車輛、無(wú)延遲進(jìn)出停靠站)的γ相比，理想停靠站的γ比普通停靠站大，這種差異來(lái)源于車輛擁堵造成的允許公交流量損失.表3中數(shù)值顯示了允許公交流量由于擁堵減少的百分比［14］.

首先，在給定c的情況下，比較表中任意一列可得，允許公交流量的損失隨CS的增大而增大.這揭示了公交車擁堵程度隨公交車服務(wù)時(shí)間的變化規(guī)律.

第二，給定CS和，c=3時(shí)，允許公交流量的降低比c=2時(shí)更為明顯.因此，泊位的增加會(huì)加重?fù)矶聠?wèn)題.

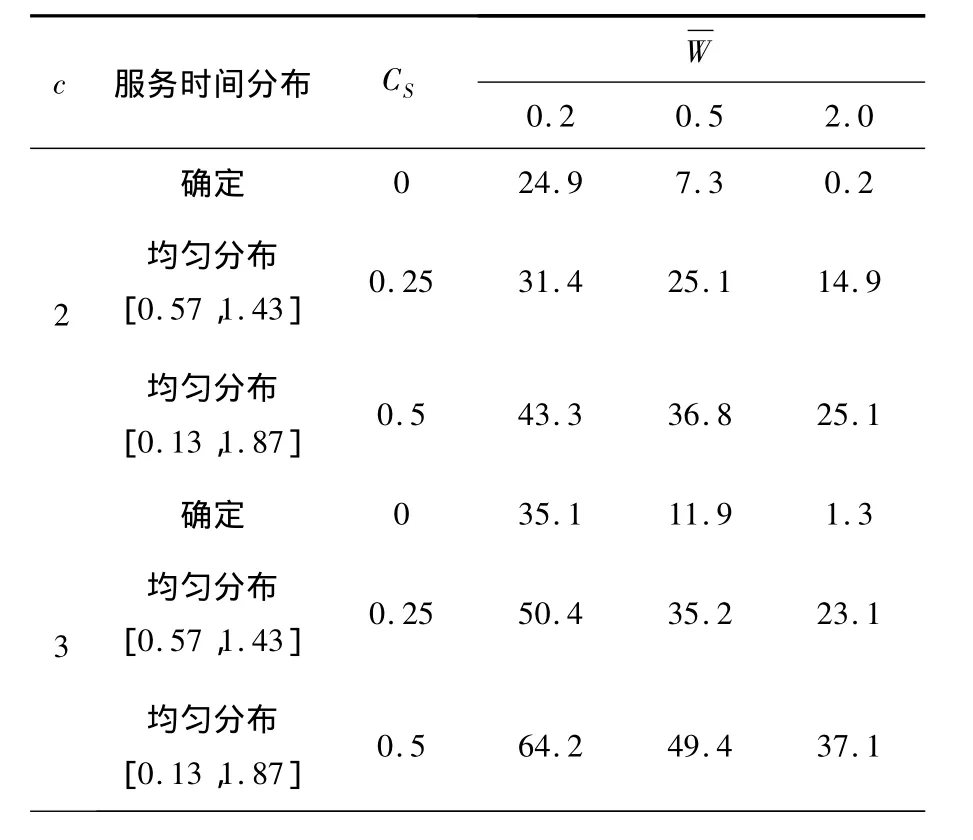
表3 車輛擁堵對(duì)停靠站允許公交流量造成的相對(duì)損失%

4 結(jié)論

(1)以排隊(duì)論為基礎(chǔ)，將馬爾可夫鏈嵌入公交車排隊(duì)過(guò)程，假設(shè)公交車的到達(dá)符合泊松分布、停靠站用于上下客的公交車服務(wù)時(shí)間為獨(dú)立同分布，推導(dǎo)出了普遍適用的公交停靠站通行能力的理論模型;

(2)該模型揭示了服務(wù)時(shí)間的變化對(duì)通行能力的影響，并表明時(shí)間管理方案的價(jià)值.研究表明，該模型尤其適用于多泊位停靠站;

(3)通過(guò)與仿真結(jié)果的對(duì)比發(fā)現(xiàn)，該模型能夠較好地反映泊位數(shù)和服務(wù)時(shí)間變化對(duì)通行能力的影響.該模型較現(xiàn)有的公交停靠站設(shè)計(jì)和分析方法更為合理，能更好的適應(yīng)公交停靠站的規(guī)劃設(shè)計(jì)以及實(shí)際交通狀況.在誤差可接受范圍內(nèi)，為停靠站運(yùn)營(yíng)人員提供了一個(gè)簡(jiǎn)單快速的方法來(lái)設(shè)計(jì)停靠站或評(píng)估停靠站成本損失.同時(shí)可應(yīng)用于其他串行排隊(duì)系統(tǒng)，如出租車排隊(duì)和公路收費(fèi)站等.

［1］MANUAL H C.Highway capacity manual［M］.［s.l.］:［s.n.］，2000.

［2］FERNáNDEZ R.Modelling public transport stops by microscopic simulation［J］.Transportation Research Part C:Emerging Technologies，2010，18(6):856-868.

［3］龔曉嵐，魏中華.基于Vissim的公交停靠站有效泊位數(shù)分析［J］.交通與計(jì)算機(jī)，2009，27(2):140-142.

［4］孫鋒，王殿海，馬東方.直線型公交停靠站通行能力計(jì)算方法［J］.西南交通大學(xué)學(xué)報(bào)，2013(3):546-552.

［5］楊群，晏秋.公交停靠站通行能力分析［J］.道路交通與安全，2010(5):49-51.

［6］ESTRADA-ROMEU M，ORTIGOSA J，ROBUSTE F.Tandem bus stop capacity［C］//Transportation Research Board 90th Annual Meeting，2011 .

［7］鄭建湖，林小惠，鄭禮席，等.基于馬爾可夫鏈模型的交通擁擠狀態(tài)預(yù)測(cè)［J］.交通標(biāo)準(zhǔn)化，2012，22:76-79.

［8］劉娟.有負(fù)顧客的M/G/1重試可修排隊(duì)系統(tǒng)的極限分布［J］.華東交通大學(xué)學(xué)報(bào)，2007，24(1):165-167.

［9］劉宗明，賈志絢，李興莉.基于灰色馬爾科夫鏈模型的交通量預(yù)測(cè)［J］.華東交通大學(xué)學(xué)報(bào)，2012，29(1):30-34.

［10］KENDALL D G.Stochastic processes occurring in the theory of queues and their analysis by the method of the imbedded Markov chain［J］The Annals of Mathematical Statistics，1953，24(3)，338-354.

［11］吳彪，齊英杰.公交停靠站車輛延誤的調(diào)查分析與對(duì)策［J］.城市公共交通，2009(6):27-29.

［12］NOZAKI S A，ROSS S M.Approximations in Multi-Server Poisson Queues［R］.California University Berkeley Operations Research Center，1976.

［13］JACQUES K S，LEVINSON H S.Operational analysis of bus lanes on arterials［M］.US:Transportation Research Board，1997.

［14］李凱勝，馮佳，李夏苗.多線路公交停靠站的設(shè)置研究［J］.交通運(yùn)輸系統(tǒng)工程與信息，2011，11(S1):187-193.