某內燃機車司機室聲固耦合噪聲仿真分析

孫春飛，王 娟，李明海

(大連交通大學 交通運輸工程學院，遼寧 大連 116028)＊

0 引言

隨著軌道交通事業的發展，列車工作人員對自身工作環境的要求也越來越高，司機室是司乘人員工作的主要場所，司機室環境是否舒適直接關系到司乘人員的身心健康、工作效率和列車運行質量.給司乘人員營造一個良好的工作環境，不僅能夠保證司乘人員的身心健康，而且能夠提高司乘人員的工作效率、操作的準確性和他們對機車的認可程度［1］.因此，做降低機車司機室的噪聲污染、改善司乘人員工作環境方面的研究是非常有意義的.

內燃機車司機室的噪聲源主要有:柴油機、主發電機、輔助電機、風機和輪軌［2］.這些設備或結構的振動通過底架和轉向架到達司機室，引起司機室的振動，隨之產生噪聲［3］.如果司機室結構模態和空腔的聲學模態在某頻率時達到了一致，結構的振動將與附近的空氣相耦合，產生的振動噪聲將急劇升高，所以，在設計和優化過程中為了更好的控制司機室的噪聲和振動，對其進行結構模態和聲學模態的分析就顯得尤為重要［4］.本文將在結構模態和聲學模態的基礎上對司機室的耦合模態以及聲場響應做詳細的計算分析，為后續的改進和優化提供必要的參考依據.

1 司機室噪聲預估

本文以東風系列某內燃機車為例進行了分析研究，根據設計圖紙對未安裝設備的機車白車身進行了三維建模，底架考慮了側梁、前后四組旁承橫梁、牽引梁、前后柴油機安裝梁以及風道梁等主要梁結構，對司機室的鋼架結構做了詳細的建模.機車白車身有限元模型圖，如圖1所示.

圖1 內燃機車白車身有限元模型

司機室空腔的聲學有限元模型如圖2(a)所示，采用的四面體網格單元，根據每個波長內至少容納6個單元的要求，需結合自身聲學計算的要求來調整網格單元大小水平［5］，經計算本模型單元可計算的最高頻率為 923.5 Hz，可以滿足400Hz以下計算要求.聲學有限元模型節點數為129 880，單元數為609 408.機車總體結構由大量的板梁結構焊接而成，車身的蒙皮均采用2.5 mm厚的鋼板，為了減少出現大量的局部模態，在不影響計算精度的情況下，有限元模型中去除了其他艙室的側墻、頂棚和鋼結構骨架，只保留了司機室的詳細鋼架結構，蒙皮、以及對其模態影響較大的底架鋼結構.節點總數為 269 878，單元數為281565.統一采用 shell181單元，材料選用鋼材料，彈性模量為2.1 ×1011N/m3，泊松比為0.3，密度為7 800 kg/m3.

計算聲固耦合模型時利用了模態疊加法，控制模態參與系數為未知量.對于聲學模態，利用司機室空腔聲學模態計算結果;對于結構模態則利用機車整車結構有限元模型的模態計算結果，這就是聲固耦合模型的構成［4］，如圖2(b)所示.

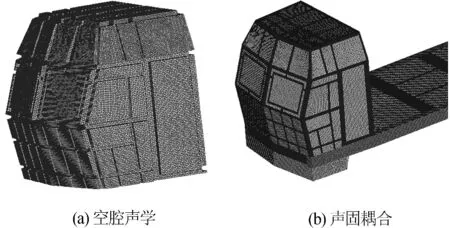
圖2 司機室兩種有限元模型

應用LMS-virtual lab進行聲場響應計算，在柴油機安裝梁上加載X、Y、Z三個方向的單位激勵載荷如圖3所示［6］，計算司機室前200 Hz的聲場響應，并且提取主駕駛員右耳處的聲壓級如圖4所示.

圖3 激勵加載圖

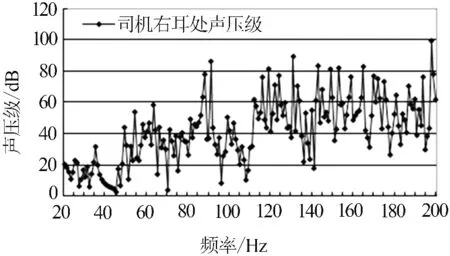
圖4 右耳處聲壓響應

從聲學計算的結果來看自90 Hz以后聲壓出現較為明顯的峰值，表現較為明顯的頻率值主要有88、91、116、119、131、143、164、198 Hz.峰值出現的原因大體分為聲學共振和結構共振兩種，具體是由于哪一種共振引起的，需要對計算時結合的結構模態、聲學模態以及耦合模態進行較為詳盡的分析.

2 模態分析理論

2.1 聲學模態理論

在理想流體媒質中，聲音傳播無衰減波動方程為:

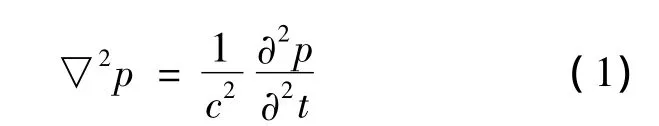
其中，c為流體介質中的聲速;p為瞬時聲壓;▽2為拉普拉斯算子.按有限元方法將司機室聲場離散化，得到離散的波動方程矩陣形式為:

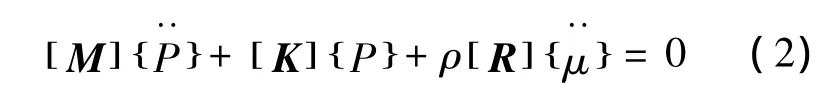
式中，［M］為流體質量矩陣;［K］為流體剛度矩陣;ρ［R］為單元耦合質量矩陣.

聲學模態分析是對聲波控制方程廣義向量為零向量的計算求解，即邊界元的結構向量為零向量，此時有限元波動方程為:

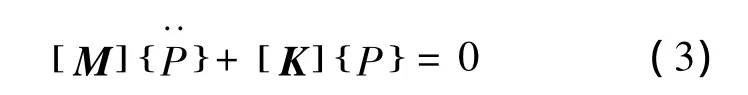
令 P =pejwt，則上式特征方程為，由此可求出聲學空腔的自鳴頻率，將其帶入式(3)中，可得聲壓P，即聲學空腔的聲壓分布.

2.2 耦合模態理論

不考慮聲壓對結構振動的影響時，結構振動的控制方程為:

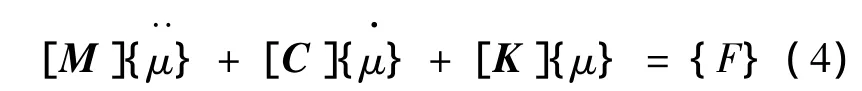
式中，［M］為質量矩陣，［C］為結構阻尼矩陣，［K］為結構剛度矩陣，［F］結構激勵力矩陣.為了完整描述整個流體-結構耦合問題，還必須考慮聲壓對結構振動的影響，這時還需在界面上加上流體壓力載荷向量，此時的結構動態有限元方程為:

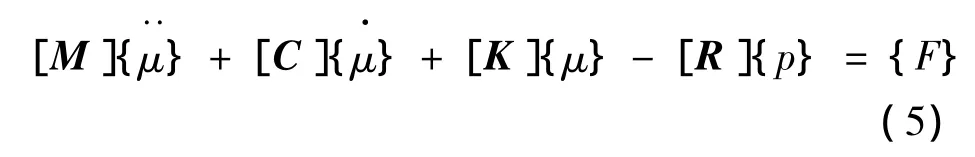
將式(2)與式(5)聯合得到完整的流體-結構耦合問題的有限元方程:

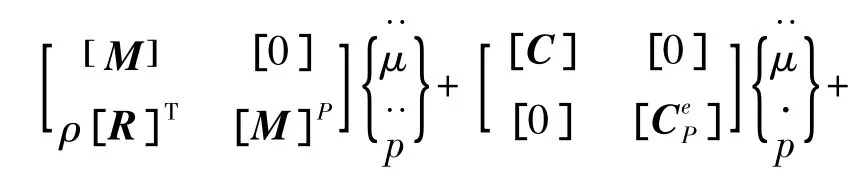
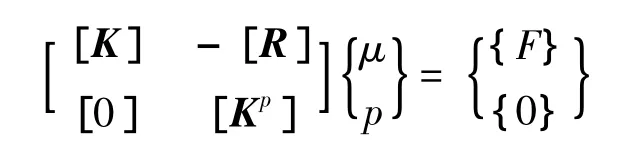
3 模態分析

3.1 空腔聲模態計算結果

司機室空腔聲模態對于司機室的設計研發及改良優化提供了很有價值的參考信息.設計人員可以在避免車身壁板與室內空腔產生共振的問題上加以研究，另外，聲模態可以確定室內空腔是否被激起了強烈的聲學共振［7］.表1中列舉了分析結果中有代表性的幾階聲學模態.

表1 聲模態部分分析結果

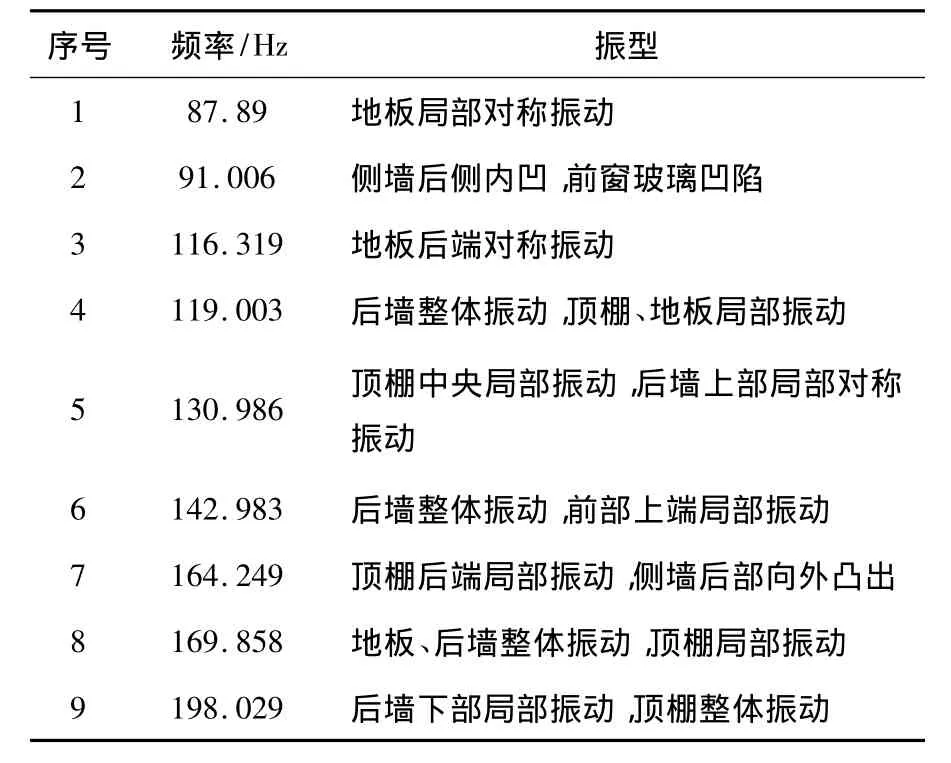
表2 耦合模態部分分析結果

3.2 耦合模態計算結果

由于車身結構中大量薄板件的存在，忽略其他艙室側墻及頂棚的影響下，模態密集現象有所緩解但仍然存在.根據后續聲學計算的結果，表2中列舉了對聲場影響較大的幾階耦合模態結果.

由司機室結構模態的頻率及振型的分析結果來看，司機室整體剛度是達標的，在60 Hz以下是趨于穩定的，但由于司機室存在很多薄板結構，模態密集.根據噪聲產生的機理來看，當這些局部模態頻率被激發，壁板的振幅驟增，司機室內的輻射噪聲升高非常明顯.若壁板振動與內部聲腔恰好耦合時，引起強烈的空腔共鳴，司機室內的聲壓級將會更劇烈的升高.諸如116、143、198 Hz周圍聲模態和耦合模態的頻率十分接近，極有可能在此處引起結構與內部聲腔的強烈共鳴，司機室內部聲壓在此產生峰值.

4 振動響應及聲學響應分析

4.1 振動響應分析

振動響應的分析是驗證噪聲預測當中峰值出現的原因是否是由模態頻率的激發所致的有力證據，所以需要對結構的振動響應進行分析［8］.

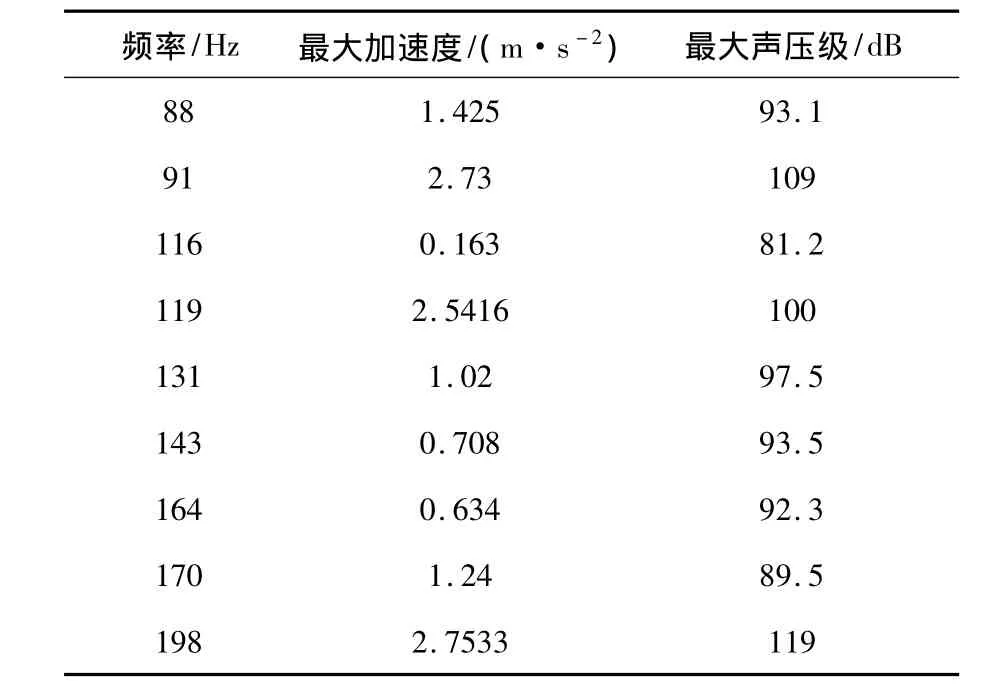
表3 最大振動響應與最大聲壓級對比

表3提供了產生聲壓峰值的頻率值所對應的振動響應和聲壓值，由振動響應的結果分析可知，存在很劇烈的聲壓峰值的頻率點都伴隨有強烈的結構振動，而且耦合模態的振型與振動響應的云圖非常接近.如:91、119、131、143、170、198，圖5 和圖6為91和119 Hz的模態振型和振動響應對比.從表格總體對比來看，振動響應的加速度越大，其聲壓級也就越大，但其中也存在諸如116、131、143和164 Hz處，振動響應較小的情況下產生了很明顯的聲壓峰值，需要進一步進行分析討論.

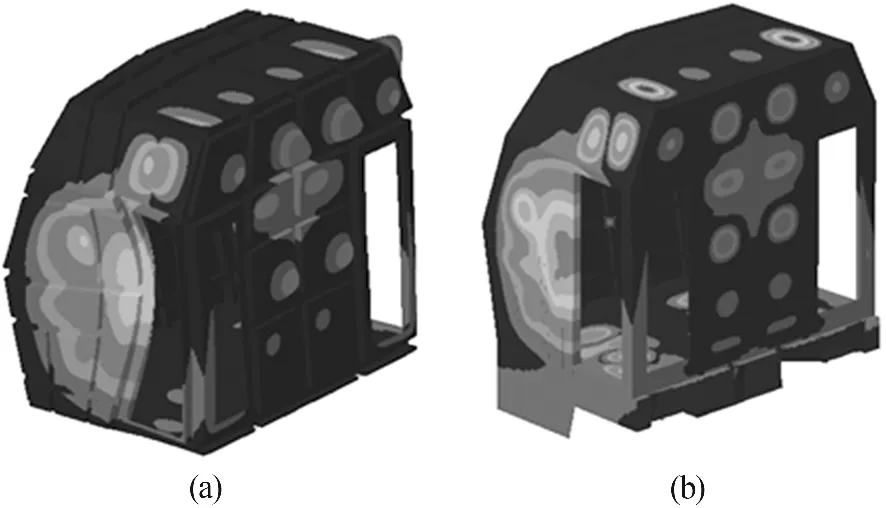
圖5 91.006 Hz耦合模態和91Hz振動響應云圖

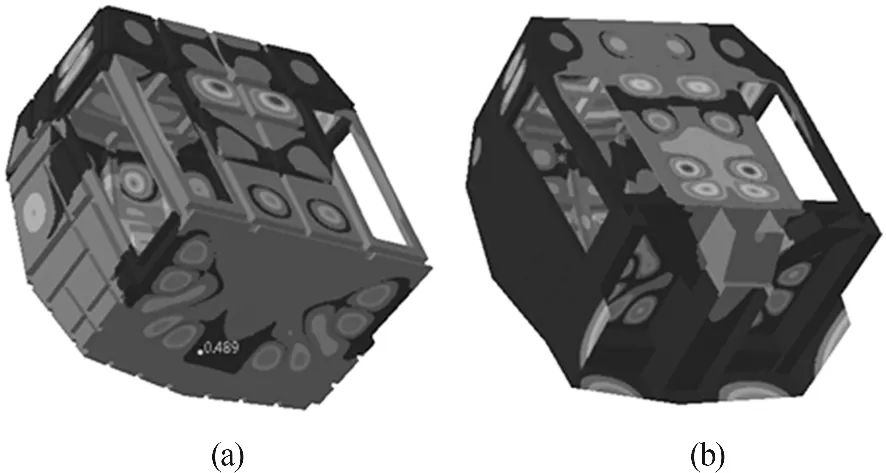
圖6 119.265 Hz耦合模態和119Hz振動響應云圖

4.2 聲場響應分析

由聲學模態及耦合模態的分析結果可以看出:116、131、143以及164 Hz處耦合模態和聲學模態的數值非常接近.對于116和143 Hz兩個頻率響應，從如圖7、圖8所示聲學模態和聲壓級云圖的情況來看，二者振型基本一致，在此處空腔的聲學模態被劇烈激發，從而在振動響應不太大的情況下產生了尖銳的聲壓峰值.

131和164 Hz處聲模態與聲場響應云圖局部一致，說明結構壁板與聲腔發生了部分耦合，導致了聲壓級也相對較高.

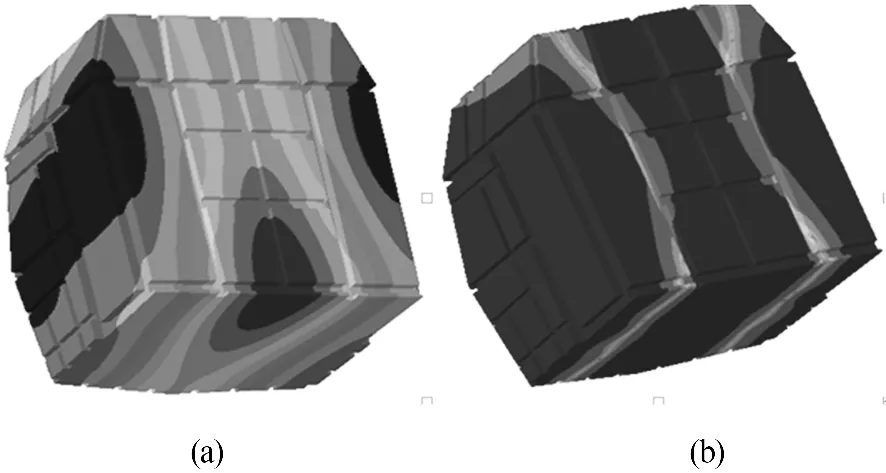
圖7 116.334Hz聲模態振型和116Hz聲學響應云圖

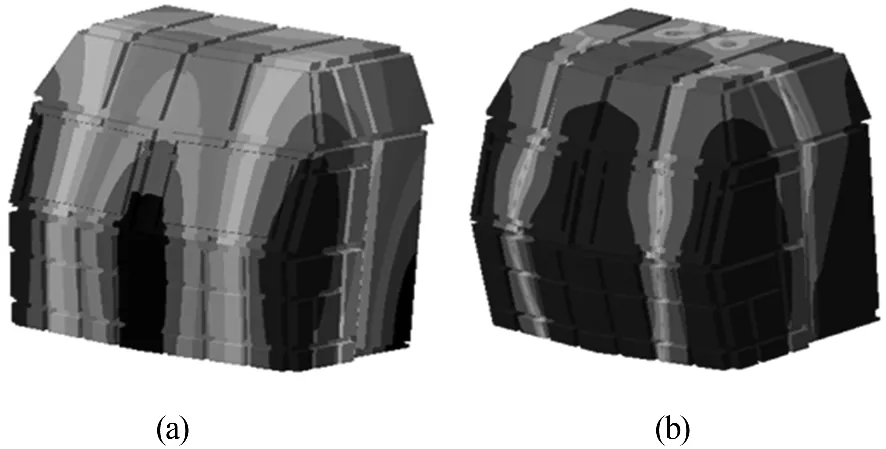
圖8 143.194Hz聲模態振型和143Hz聲學響應云圖

5 結論

(1)沒有結構共振及聲學共振的參與的情況下，振動的加速度(幅值)越大，司機室的聲壓級越大;

(2)司機室壁板共振是導致91、119、131、143、170，198處產生聲壓峰值的主要原因;

(3)司機室的壁板振動與室內空腔的聲模態完全或部分耦合導致了聲腔共鳴，激發了聲模態導致了116、131、143以及164 Hz在振動幅值不大的情況下聲壓較大;

(4)司機室的地板在耦合模態分析過程中是導致模態密集重要原因之一，在振動響應分析中振動幅度較大，對司機室聲壓的貢獻度較大.

［1］馬天飛 ，林逸 ，張建偉 .轎車車室聲固耦合系統的模態分析［J］.機械工程學報 ，2005，41(7):225-230.

［2］張萍，劉巖.內燃機車司機室噪聲特性及吸聲材料研究［J］.內燃機車 ，2006(12):16-17.

［3］徐浩，張代勝 .輕卡駕駛室聲固耦合系統動態特性分析［J］.汽車科技 ，2012(5):18-22.

［4］曹友強 ，鄧兆祥 .車內耦合聲場預測研究［J］.汽車工程 ，2008，30(5):483-487 ，538.

［5］朱茂桃 ，樊婷.微型電動轎車駕駛室內的低頻噪聲分析［J］.噪聲與振動控制 ，2012(4):96-102.

［6］謝素明 ，付亞蘭 ，王悅東，等 .鐵路客車結構 -聲耦合系統的聲學特性［J］.大連交通大學學報 ，2008，29(5):40-44.

［7］劉云 ，蹇興東 .基于Hypermesh和ANSYS的拖拉機駕駛室模態分析［J］.中國機械工程，2010(5):1121-1124.

［8］詹福良，徐俊偉 .Virtual.lab Acoustics聲學仿真計算從入門到精通［M］.西安:西北工業大學出版，2013.