非線性擴(kuò)散作用下一類四階拋物方程解研究

梁 波，沈慧穎

(大連交通大學(xué) 理學(xué)院，遼寧 大連 116028)*

非線性四階拋物方程的研究最近受到關(guān)注，形如ut+(upuxxx)x=0及=0的類型的方程可用來描述非常薄的粘性可壓縮流體沿著斜面運(yùn)動(dòng)的情況，其中未知函數(shù)u代表流體薄層的的厚度(可參考文獻(xiàn)［1-2］).Bernis等人［3］在分?jǐn)?shù)次連續(xù)函數(shù)空間中證得了弱解的存在性.文獻(xiàn)［4-5］還對(duì)解的長時(shí)間行為等問題進(jìn)行了研究.

本文主要研究一類帶有非線性二階擴(kuò)散項(xiàng)的四階拋物方程，形式如下:

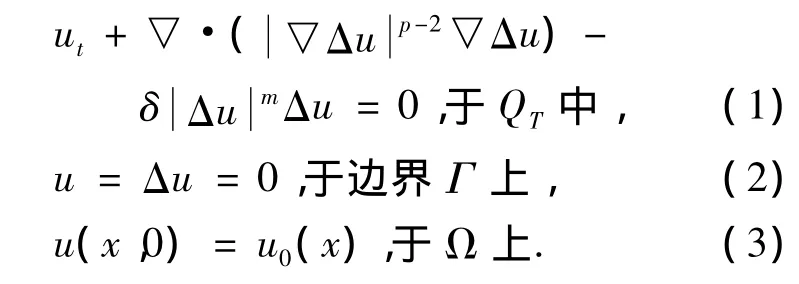
這里Ω是RN中的一個(gè)有界開區(qū)域，QT=Ω×(0，T)，Γ=?Ω × (0，T)，?Ω∈C1，p ＞ 1，m≥0.為敘述方便，下面引入兩個(gè)符號(hào)定義:

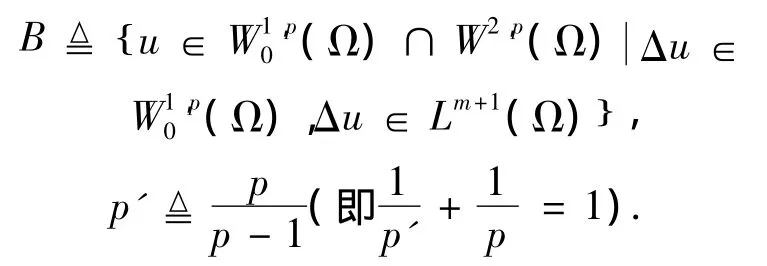
利用半離散方法可得到解的存在性如下:

定理1(存在性) 方程(1)～(3)存在弱解滿足:

(1)ut∈Lp'(0，T;W0-1，p'(Ω))，u ∈ L∞(0，T;H10(Ω))∩C([0，T];L2(Ω))，Δu∈Lp(0，T;W10，p(Ω))，Δu∈ Lm+2(QT);

(2)對(duì)任意的φ∈C∞0(QT)，有

利用檢驗(yàn)函數(shù)法可獲得解的唯一性定理:

定理2(唯一性)(1)～(3)的解是唯一的.

1 定態(tài)解的存在性

本節(jié)來研究對(duì)應(yīng)的定態(tài)問題:

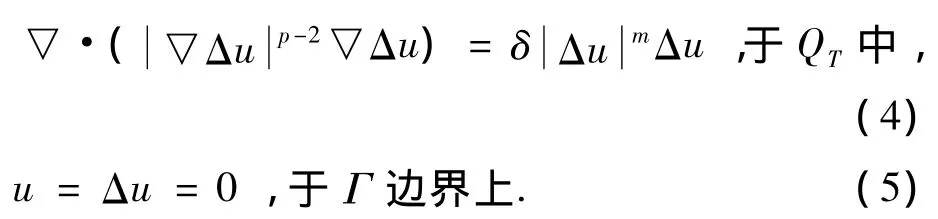
定義泛函

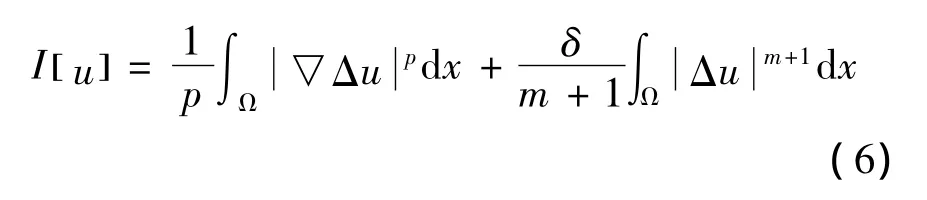
其中，φ∈C∞0(Ω)為任一檢驗(yàn)函數(shù).

0 引言

由下確界定義，存在子列 { uk}∞k=1? B，使得I[ uk]→vinBf[v] ，(k → ∞).所以 ‖▽?duì)k‖LP(Ω)∈≤ C ，‖Δuk‖Lm+1(Ω)≤ C .利用 Poincare不等式及二階橢圓方程的Lp-估計(jì)，可得

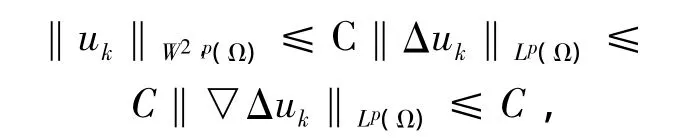
所以，存在 {uk}的一個(gè)子列及u∈B，使得

uk→弱u于W1，p0(Ω)∩W2，p(Ω)，

Δuk→弱Δu于W1，p0(Ω)，

Δuk→弱Δu于Lm+1(Ω).

2 拋物問題的存在性

考慮離散問題如下

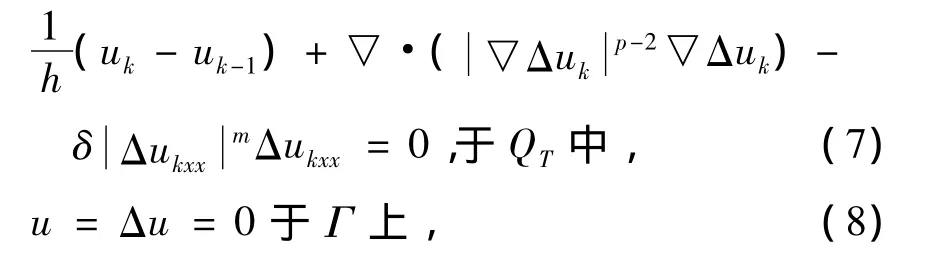
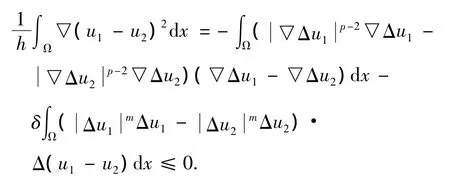
為證明定理1，以(7)～(8)為基礎(chǔ)定義近似解如下

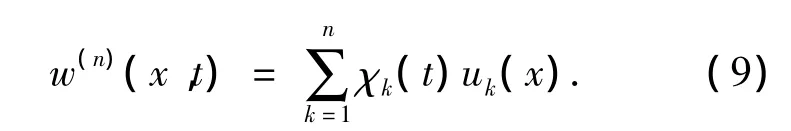
χk(t)是時(shí)間區(qū)間 ((k-1)h，kh］，k=1，2，……，n上的特征函數(shù)，為獲得逼近解的收斂性，我們需要一些一致估計(jì).

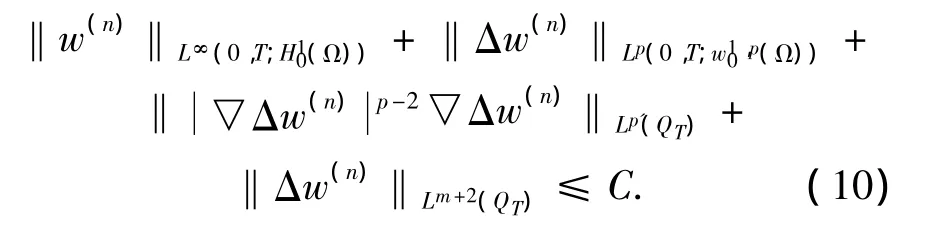
引理2 對(duì)于近似解(9)，下面的正則估計(jì)成立證明 類似參考文獻(xiàn)［6］的證明思路，以Δuk為(7)～(8)的檢驗(yàn)函數(shù)，并利用(9)易知因 此 ‖▽w(n)‖L∞(0，T;L2(Ω))≤ C.同 時(shí) 可 知.其余估計(jì)類似文獻(xiàn)［6］，得證.

定義第二類近似解如下

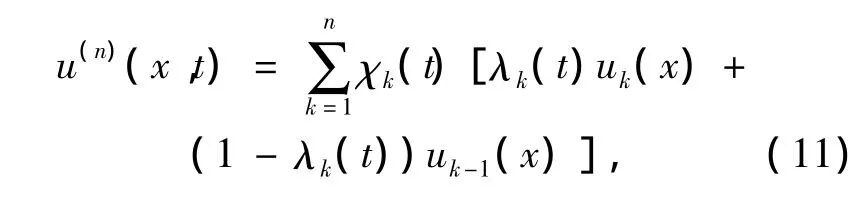
這里

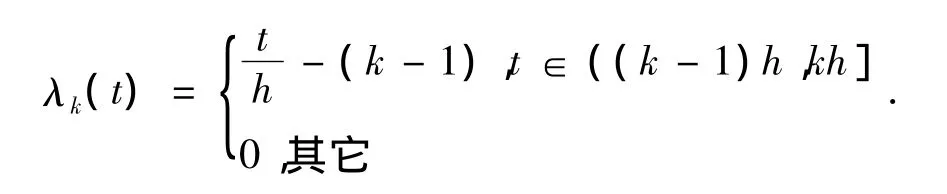
對(duì)此近似解有如下估計(jì).

引理3 下面的一致估計(jì)成立，

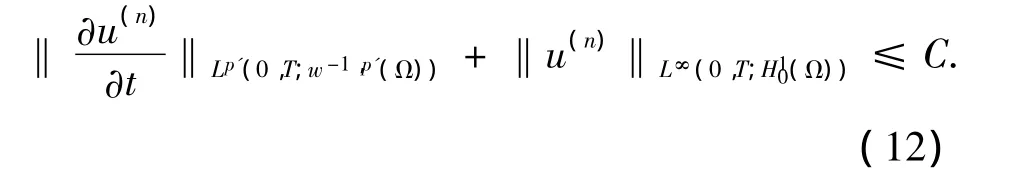
證明 由于

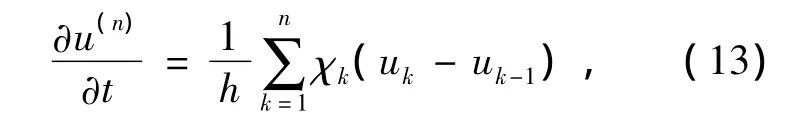
對(duì)任意的 φ ∈ w1，p0(Ω)及 ‖φ‖w1，p0(Ω)≤1 ，由(10)可知

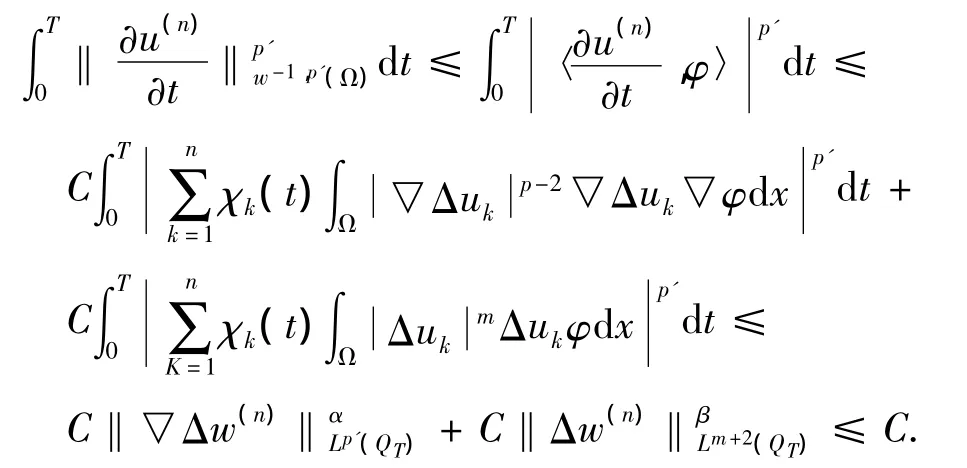
其中α和β為某正指數(shù).根據(jù)u(n)的定義

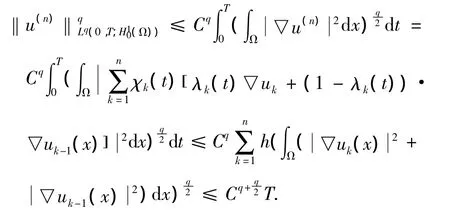
定理1的證明:根據(jù)能量估計(jì)(10)，存在w(n)的一個(gè)子列及泛函v，使得當(dāng)n→∞ 時(shí)

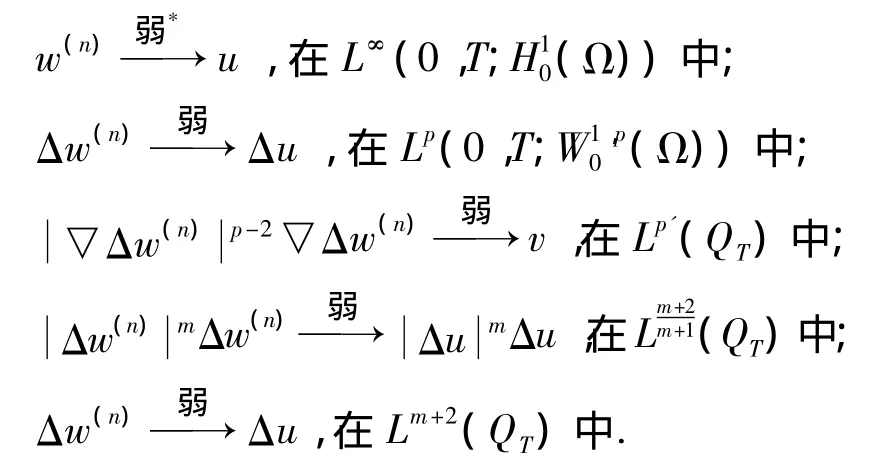
存在足夠大的整數(shù)r＞0，使得w-1，p'(Ω)→H-r(Ω).由Aubin'sLemma［7］，嵌入H10(Ω)→緊L2(Ω)→H-r(Ω)及一致估計(jì)(12)，則u(n)存在子列使得當(dāng)n→∞時(shí)

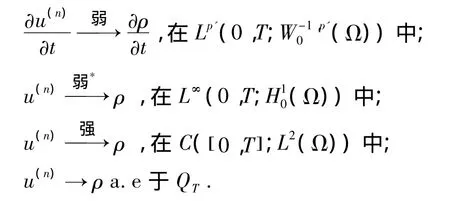
利用u(n)和w(n)的定義可知，對(duì)于任意的φ∈C∞0(QT)，

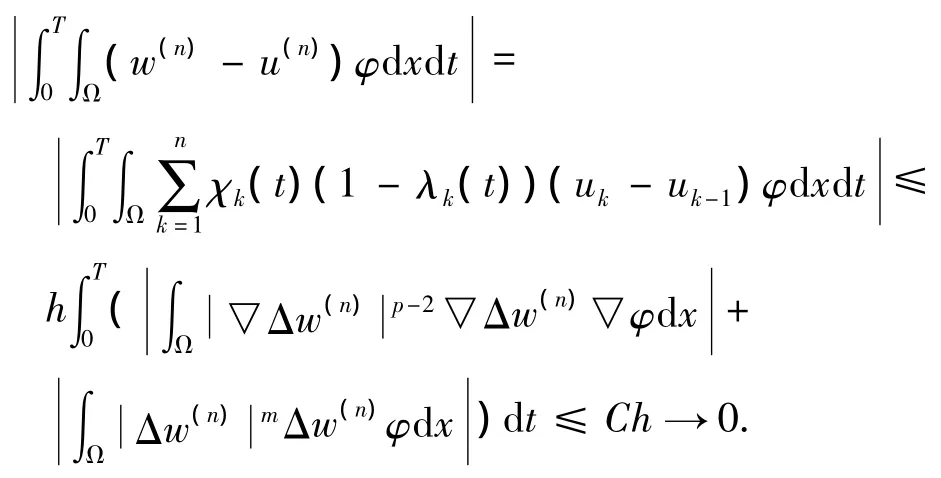
因此ρ=u a.e于QT中.

對(duì)任意的檢驗(yàn)函數(shù)φ，有

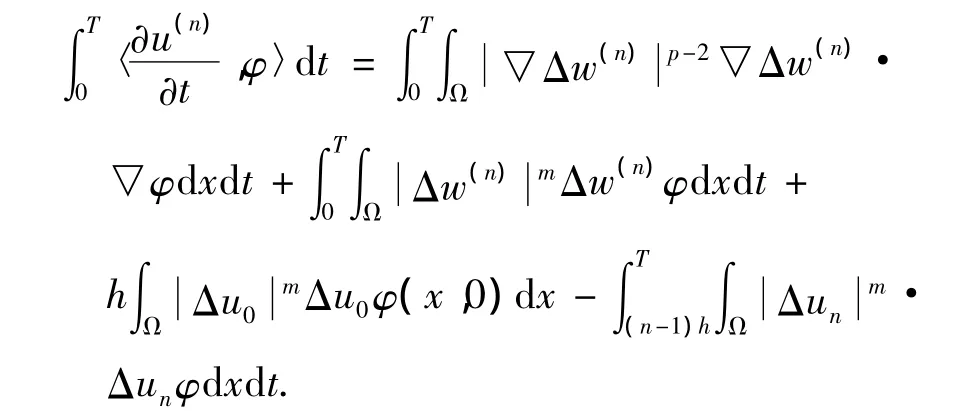
令n→∞得到

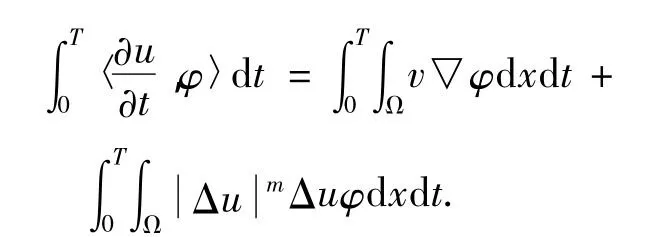
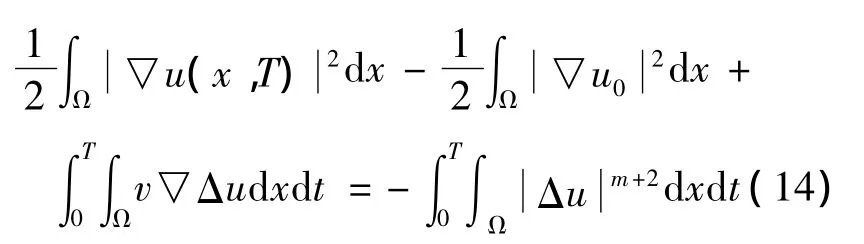
另一方面，

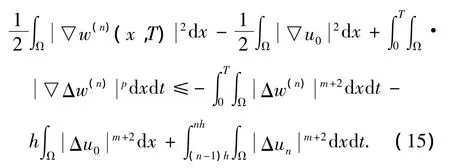
注意到

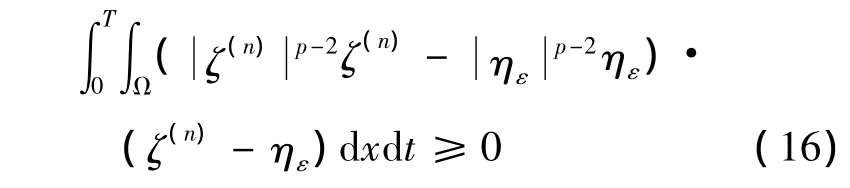
取ζ(n)=▽?duì)(n)，ηε=▽?duì)?u-εφ)(對(duì)于任意的φ及ε＞0)，由(15)～(16)知當(dāng)n→∞ 時(shí)

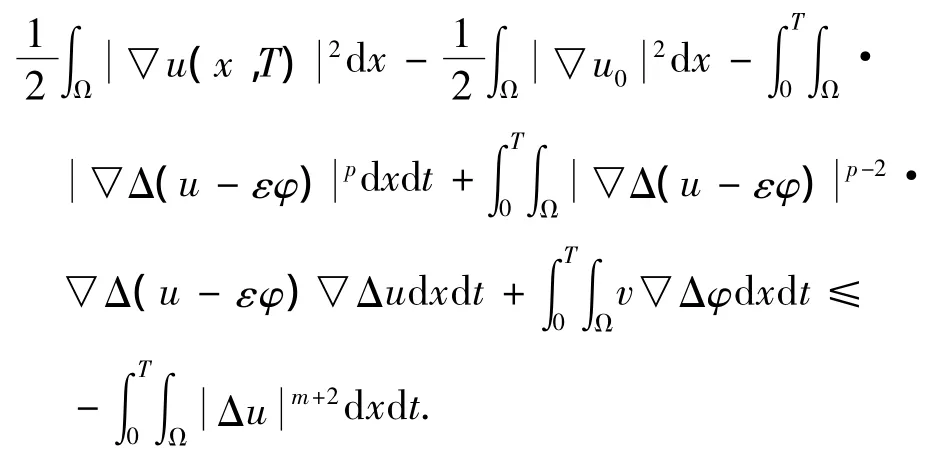
再由(14)得

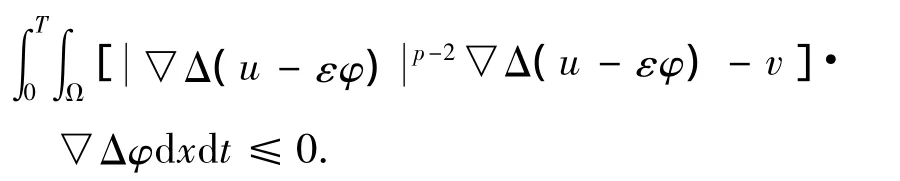
當(dāng)ε→0時(shí)，得到

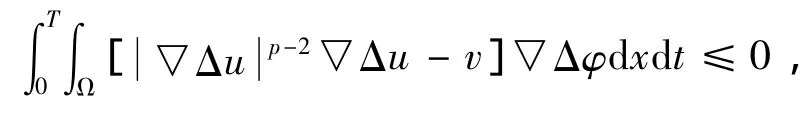
利用φ的任意性可知 ▽?duì)p-2▽?duì)=v幾乎處處于QT.唯一性容易證明，這里省略.

［1］CAHN J M，HILLIARD J E.Free energy of a non-uniform system I，Interfacial free energy［J］.J.Chem.Phys，1958，28:258-367.

［2］MYERS T G.Thin films with high surface tension［J］.SIAM Rev，1998，40:441-462.

［3］BERNIS F，F(xiàn)RIEDMAN A.Higher order nonliear degenerate parabolic equations［J］.J.Differential Equations，1990，83:179-206.

［4］CARLEN E A，ULUSOY S.An entropy dissipation estimate for a thin film type equation ［J］.Commun.Math.Sci，2005(3):171-178.

［5］KING JR.Two generalization of the thin film equation［J］.Math.Comput.Modelling，2001，34:737-756.

［6］LIANG B，ZHENG S.Existence and asymptotic behavior of solutions to a nonliear parabolic equation of fourth order［J］.J.Math.Anal.Appl.，2008，348:234-243.

［7］SIMON J.Compact sets in the spaceLp(0，T;B)［J］.Ann.Mat.Pura appl.，1987，146:65-96.