基于順路原則及位置預估的動態調度策略

曹劍東，李家文

(1.交通運輸部 科學研究院，北京 100029；2.浙江工業大學 機械工程學院,杭州 浙江 310014)

基于順路原則及位置預估的動態調度策略

曹劍東1，李家文2

(1.交通運輸部 科學研究院，北京 100029；2.浙江工業大學 機械工程學院,杭州 浙江 310014)

摘要：針對市內貨物配送和收集這一典型的集送貨問題，在利用“混合禁忌搜索算法”進行靜態調度求解的基礎上，提出基于“順路原則”的局部調整策略實現集送貨問題的動態調度計算.計算過程中采用模糊推理方法選擇局部調整范圍，同時采用車輛位置預估方法消除計算、傳輸和執行延遲帶來的車輛位置的變化對優化結果的影響.以40個遍布于北京的客戶構成的集送貨問題為例，驗證了動態調度策略的有效性。

關鍵詞：運輸經濟；動態調度；順路原則；模糊推理；集送貨

Dynamic dispatch strategy based on by-way principle

and location pre-estimation

CAO Jiandong1, LI Jiawen2

(1.China Academy of Transportation Sciences, Beijing 100029, China;

2.College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:In order to solve the typical problem for urban cargo pickup and delivery, dynamic dispatch calculation is proposed by local adjustment strategy called as “by-way principle”, which is based on static dispatch solutions worked out by hybrid tabu search algorithm. Local adjustment range is selected using fuzzy reasoning method in calculation progress and influence of vehicle location change due to calculation, transmission and performance delay is lessened using pre-estimation method to determine vehicle location. Calculation obtained for a pickup and delivery problem example with 40 customers in Beijing validates the efficiency of dynamic dispatch strategy。

Keywords:transport economy; dynamic dispatch; by-way principle; fuzzy reasoning; pickup and delivery

配送和集貨是物流中的一個重要環節，是貨物在物流結點與收發貨人之間流動的過程[1].對運輸車輛的行駛線路進行有效的優化調整，可大幅減少車輛的空駛里程.集送貨問題可以分為靜態調度和動態調度兩類.在靜態調度方面，唐俊、楊浩雄、王飛、鄭四發[2-6]等采用粒子群算法、蟻群算法和禁忌搜索算法對該問題進行研究并取得不錯的效果。

在集送貨動態調度方面，其主要的優化策略包括兩類，即“重新優化策略”和“局部調整策略”.“重新優化策略”實際上可以看作是動態調度問題的一種靜態的求解策略，其計算量大，時效性低，因此不適于實時性要求高的動態調度計算.局部調整與重新優化原理不同，是根據接收到的動態信息對現有行駛路徑進行局部改進.Madsen等人[7]提出插入法求解運送老人和殘疾人的問題，Gendreau等[8]針對一類比較特殊的信使服務優化調度問題，提出一種適應存儲的改進禁忌搜索算法.但是上述算法優化大規模的實際集送貨問題時在計算時間和精度方面很難兼顧，另外，算法忽略由于計算、傳輸和執行的延遲導致車輛位置變化而產生的誤差，將進一步降低優化精度.針對集送貨動態調度問題，在采用車輛位置預估方法估計車輛當前位置和采用模糊推理方法選擇局部調整范圍的基礎上，應用基于“順路原則”的局部調整策略實現集送貨問題的動態調度計算.40個客戶的計算實例表明：動態調度策略能夠在保證計算效率的前提下，提高計算精度和結果的可執行性。

1基于局部調整策略的動態調度算法

1.1集送貨靜態路徑方案的構造

市內貨物的配送和收集是一個典型的車輛路徑問題，具有“帶時間窗約束”、“單一車場”、“涉及多種車型”以及“取貨和送貨一體化完成”等四個典型特征。

考慮到集送貨問題的復雜性、典型性和特殊性，以運輸車輛的燃油成本Cg、折舊成本Ct、車廂整理成本Cs以及司機工資成本Cd之和為目標函數，建立該調度問題的成本模型：

(1)

C(k)=Cg(k)+Cd(k)+Ct(k)+Cs(k)

(2)

(3)

Di(k)=d(nk,i-1,nki)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

式中：變量i，j和k的取值范圍分別為i=1,2,…,N，j=1,2,…,N，k=1,2,…,M，N為當前所需服務的客戶總數，M為配送中心當天最多可用的車輛總數，假設各待服務客戶的序號為i，其中i=0表示第i個待服務客戶為配送中心；h(i)表示第i個客戶的收貨重量；g(i)表示第i個客戶的發貨重量；nkj為車輛k的行駛路徑上客戶j的實際編號；Nk為車輛k的行駛路徑包含的路段總數。

式(3~7)為運輸車輛燃油成本：β0為車輛空載運輸時的油耗與滿載運輸時的油耗比值；rg為燃油成本比例系數，即運輸車輛滿載行駛時單位公里的油耗成本，元/km；d(i,j)為運輸車輛從第i個客戶到第j個客戶的實際行駛距離，km；Hi(k)為運輸車輛k從第i個客戶開往第j個客戶時車上總的送貨重量，kg；Gi(k)為車輛k從第i個客戶直接開往第j個客戶時車上總的取貨重量，kg；W(k)為運輸車輛k的最大核定載重，kg。

式(8)為司機工資成本：r0表示司機單趟發車固定成本，元；rd表示司機行駛里程成本系數，元/km。

式(9)為運輸車輛折舊成本(其值與運輸車輛的行駛里程成正比)：rt為車輛折舊成本系數，元/km。

式(10)為重新整理車廂的成本：rs為被裝卸貨物的重量成本系數，元/kg，zij為客戶j處是否需要整理客戶i處收取的貨物。

考慮到靜態路徑方案是動態調度優化的基礎，它的優劣程度直接影響動態優化的結果.因此，采用“混合禁忌搜索算法”(圖1)，針對這一車輛路徑問題進行初始方案的預求解，其思路主要是先采用經過改進的Clarke-Wright節約算法[9]計算得到一個可行的初始調度方案.在此基礎上，再采用改進的禁忌搜索算法[10]對之前得到的初始調度方案進行優化改進，最終實現整個集送貨調度問題的求解.應用節約算法構造初始的可行方案的主要優勢在于“成本節約值較大的兩點將被優先選擇”，從而使得產生的初始方案更加科學合理，這使得整個問題的求解速度顯著提升.而應用改進的禁忌搜索算法對初始方案進行調整的優勢在于能夠較容易的跳出局部最優點，從而實現全局范圍內的優化搜索。

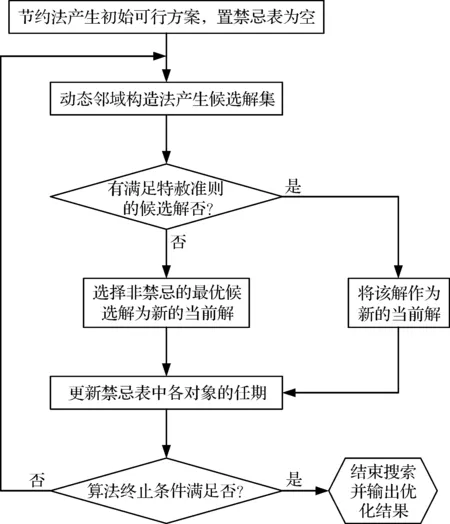
圖1　混合禁忌搜索算法框架Fig.1　Hybrid tabu search algorithm framework

1.2車輛位置的預估修正

動態調度是根據新出現客戶的信息和客戶出現時運輸車輛的當前位置進行調度計算[11].車輛的位置由車上安裝的GPS定位終端設備通過GPRS或者3G無線通信網絡發送至調度中心.然而實際工作中通常會遇到這樣的情況，當司機開始執行新的調度方案時，已經比開始調度計算的時刻T晚了一定的時間間隔ΔT，其數值主要包括動態調度計算時間、無線傳輸及司機確認時間等.在這一時間間隔ΔT之內，正在執行運輸任務的所有車輛，都有可能已經沿著原來的調度方案設定的行駛路線繼續行駛了一段距離，極端情況是甚至有可能運輸車輛已經到達某一個等待服務的客戶處并開始配送服務，從而造成新制定的動態調度計劃在執行過程出現偏差.因此，在調度計算過程中需要對車輛位置進行提前預估。

以圖2(a)為例對車輛位置的預估方法進行描述.圖中虛線條為包含客戶A和B的車輛行駛線路，粗實線為車輛在時間間隔ΔT之內的行駛軌跡.車輛位置預估方法描述如下：由車輛行駛車速和車輛預計行駛線路可分別求出車輛到達路口1，2，…，n的時間，因此可判斷車輛經過時間間隔ΔT之后的位置。

具體分兩種情況：1) 車輛位于路段上：預估的運輸車輛的位置恰好在兩個路口之間.通常路段本身的長度較小，且路段上運輸車輛的行駛方向是單一的，對后續的動態調度優化計算的影響可以忽略，因此，將路段中點作為車輛的預估位置P′.2) 車輛在客戶處，如圖2(b)所示.具體抽象方法如下：將客戶B抽象成一條路段，路段的通行時間為客戶B的裝/卸貨時間，路段兩端的路口的經緯度值均為客戶B的經緯度值。

圖2　車輛位置的預估Fig.2　Vehicle location pre-estimation

另外，考慮到時間間隔ΔT永遠小于客戶裝/卸貨時間，車輛在ΔT之內穿越某一客戶的情況不會出現，因此，預估車輛位置時不考慮此種特殊情況。

1.3基于模糊推理的局部調整范圍選擇方法

局部調整算法是在設定搜索范圍的條件下，調整現有車輛調度計劃，使該調度計劃能夠及時而準確的滿足新增加的所有客戶的動態服務需求.因此，選擇合適的調整范圍(這里主要指參與調整優化計算的線路集合)對于提升算法的精度和計算效率非常重要。

對調整范圍的選擇有較為重要影響的因素主要有兩個：即當前線路與新增加的客戶之間距離的遠近程度(定義新增加客戶至當前線路的距離為新客戶到線路上所有客戶直線距離的最小值)以及線路上車輛的平均空余體積大小，而平均空余體積的定義為

(11)

式中：Vd為線路上的送貨總體積；Vp為線路上的取貨總體積.顯然，“距離的遠近”及“平均空余體積的大小”這兩個概念是模糊的，因此筆者采用模糊推理方法來進一步確定合理的調整范圍，即判斷當前各條運輸線路是否應該位于調整范圍之內。

將兩個主要因素作為因素集合E={新客戶與線路之間的距離e1，車廂平均空余體積e2}，而將是否屬于調整范圍之內作為評價集合F={線路在調整范圍之內f1，線路在調整范圍之外f2}.因素e1和e2對評價值f1的隸屬度函數為

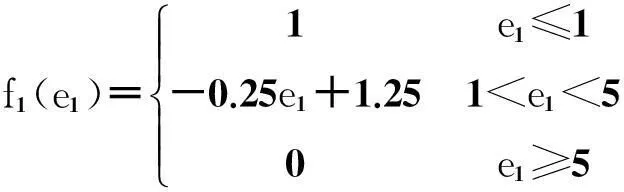
(12)

(13)

由于f1和f2是互為補集的兩個結論，因此，只需要列出e1和e2對f1的隸屬度函數。

將某一行駛線路和新增加的客戶的實際數據分別代入到兩個隸屬度函數式(12，13)，可計算得到因素e1和因素e2對評價集F的隸屬度矩陣R.另外，考慮到因素e1和因素e2對最終評價結果的影響程度也不盡相同，故需要定義兩個因素的權重矩陣A.顯然在判斷給定線路是否位于調整范圍之內時，距離因素要比空余體積因素重要，因此選定權值矩陣A=(0.7,0.3).最后，可給出模糊推理的結果為

(14)

式中參數rij為隸屬度矩陣R的元素。

根據式(14)可求得模糊推理的計算結果b1和b2.當b1>b2時，推理的結果為線路在調整范圍之內.反之，則線路在調整范圍之外。

1.4基于“順路原則”的局部調整策略

一般情況下，局部調整策略往往采用“最接近的原則”作為判斷依據來選擇合適的調整對象，即選擇某一個給定范圍之內離新增加的客戶“最近”的運輸車輛或者客戶作為局部調整對象.圖3(a)為“接近原則”的示意圖，圖3中虛線圓圈標識的新增加的客戶“9”與客戶“1”(在運輸車輛“2”的行駛線路中)的距離是相對而言最短的，因此，可以選擇客戶“1”作為此次局部調整的對象，并將新增加的客戶“9”直接插入到當前客戶“1”的前面，構造出一個新的調度優化方案.但是，由于動態集送貨調度問題的特殊性，距離的遠近通常無法有效反應新增運輸成本的大小。

與“最接近的原則”不同，“順路原則”選擇調整對象的依據是“是否順路”，即當前運輸車輛服務新增加的客戶是否“順路”.對于“順路”的含義可以理解如下：在滿足時間窗、載重、體積等約束條件的前提之下，將新增加的所有客戶依次插入至當前運輸車輛的行駛線路中，額外增加的運輸成本ΔC越小就表示運輸車輛服務新增客戶越是“順路”.ΔC的求解方法為

ΔC(x,y,z)=Cx,z+Cz,y-Cx,y

(15)

式中：ΔC(x,y,z)為將客戶z插入x和y之間時新增加的額外成本.圖3(b)為基于“順路原則”局部調整的示例，當新增加的客戶“9”被插入至運輸車輛“1”的行駛路線上的客戶“4”和客戶“2”之間的時候，額外增加的運輸成本ΔC(4,2,9)最小.因此，將安排運輸車輛“1”在完成客戶“4”的送貨任務之后“順路”行駛至新增加的客戶“9”處收取貨物。

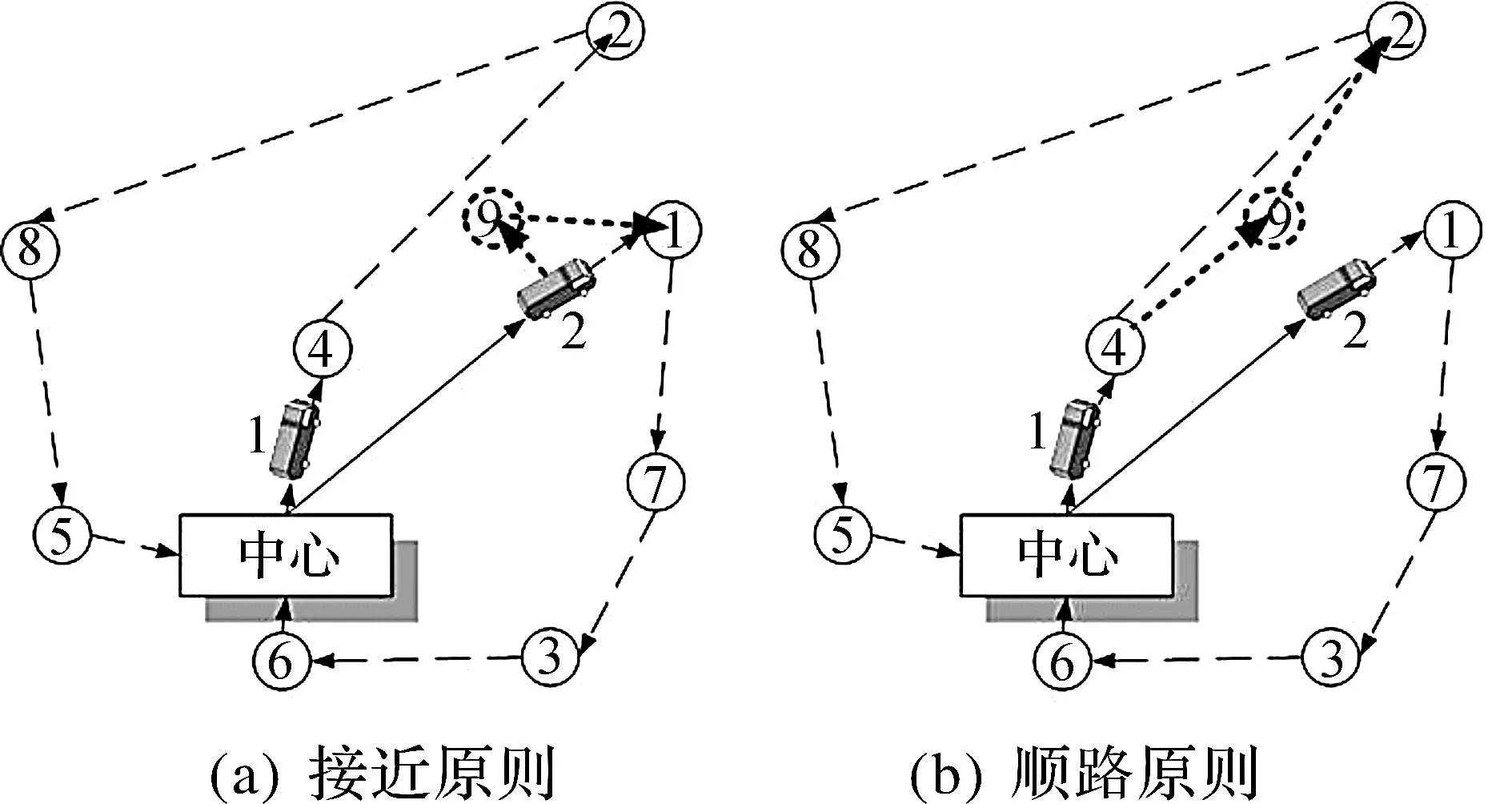
圖3　局部調整策略示意圖Fig.3　Local adjustment strategy diagram

2應用驗證

以某大型物流企業實際的集送貨動態調度問題為例，驗證基于順路原則及位置預估的集送貨動態調度策略的有效性.動態調度開始時，共有40個不同的客戶(其中只有4個客戶是新增客戶).客戶位置、車輛位置以及現有路徑如圖4所示，圖4中圓圈內的客戶即為新增客戶，另外由于顯示的原因，圖4中只加粗顯示其中的兩條路徑。

通過應用基于模糊推理方法的調整范圍選擇策略，可以確定4個新增加客戶各自的局部調整范圍.以圖4中方框內的客戶為例，采用模糊推理方法，確定其調整范圍僅限于圖中被加粗顯示的兩條路徑。

圖4　客戶位置、車輛位置以及現有路徑Fig.4　Customers location,vehicle location and directions

圖5為該動態調度問題采用基于順路原則及位置預估的集送貨動態調度策略之后的優化結果，包括：7條行駛線路(行駛線路數目并未發生改變)，總的行駛里程為495km，總成本為996 元。

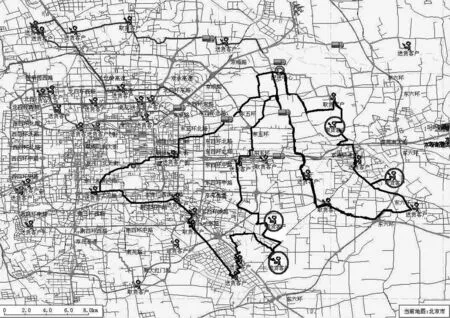
圖5　動態調整策略優化結果Fig.5　Results of dynamic dispatch strategy

表1為兩類算法的對比情況，表1中基于“接近原則”的局部調整算法的調整范圍是所有路徑.通過對比分析可知：筆者提出的基于“順路原則”的局部調算法無論在精度還是效率方面均具有明顯優勢。

表1　兩類算法對比分析

表2為車輛位置預估對調度結果的影響.通過對實際的集送貨調度數據分析，選定延遲時間ΔT=180 s，車輛當前車速是v=10 m/s.表2中位置誤差是指與GPS數據(即經過ΔT之后車輛的真實位置)的誤差，而表2中的成本是指將車輛的真實位置代入兩類優化結果之后計算得到的成本，因此，大于表1中的成本996 元.表2充分說明車輛當前位置對優化結果具有重要影響，位置預估越準確則優化結果越精確。

表2　車輛位置預估對優化結果的影響

3結論

在順路原則及位置預估的集送貨動態調度策略的基礎上，得出基于模糊推理的局部調整范圍之選擇方法和基于“順路原則”的局部調整策略能夠在保證精度的前提下，有效提高動態調度優化的效率；考慮優化過程中對車輛位置的變化及車輛位置預估方法的采用，將提高動態調度優化的精度以及優化結果的可執行性。

參考文獻：

[1]李軍，郭耀煌.物流配送車輛優化調度理論與方法[M].北京：中國物資出版社，2001：99-112。

[2]王飛.帶時間窗車輛調度問題的改進粒子群算法[J].計算機工程與應用，2014，50(6)：226-229。

[3]ZHENG Sifa, CAO Jiandong, LIAN Xiaomin. Urban pickup and delivery problem considering time-dependent fuzzy velocity[J]. Computers & Industrial Engineering，2011，60(4)：821-829。

[4]曹劍東，鄭四發，李兵，等.考慮分時模糊車速的帶時間窗的市內集送貨問題[J].系統仿真學報，2009，21(3)：823-826。

[5]胡志華，陶莎.基于混合進化算法的甩掛配送問題[J].公路交通科技，2013，30(5)：147-152。

[6]陳嶷瑛，李文斌，王舵，等.使用面向離散搜索空間的蛙跳算法求解TSP[J].計算機工程與應用,2009,45(27):50-52。

[7]MADSEN O B G, RAVN H F, VOELDS J. A heuristic method for dispatching repairmen[J]. Annals of Operations Reasearch,1995,61:193-208。

[8]GENDREAU M, GUERTIN F, POTVIN J Y, et al. Parallel tabu search for real-time vehicle routing and dispatching[J]. Transportation Science,1996(33):381-390。

[9]CLARKE G, WRIGHT J W. Scheduling of vehicles from a central depot to a number of delivery points [J]. Operations Research,1964,12(4):568-581。

[10]OSMAN I H, WASSAN N A. A Reactive Tabu search meta heuristic for the vehicle routing problem with backhauls[J]. Journal of Scheduling,2002，5(4)：263-285。

[11]李兵，鄭四發，曹劍東，等.求解客戶需求動態變化的車輛路徑規劃方法[J].交通運輸工程學報,2007,7(1):106-109。

(責任編輯：陳石平)

中圖分類號：U492

文獻標志碼：A

文章編號：1006-4303(2015)02-0197-05

作者簡介：曹劍東(1980—)，男，江蘇蘇州人，副研究員，工學博士，研究方向為智能交通，E-mail:caojiandong@catsic.com。

基金項目：國家自然科學基金資助項目(51405438)

收稿日期：2014-11-25