山嶺隧道涌水量預測方法分類及相關因素分析

顧博淵， 史寶童， 黃　嫚

(中交第一公路勘察設計研究院有限公司， 陜西 西安　710075)

?

山嶺隧道涌水量預測方法分類及相關因素分析

顧博淵， 史寶童， 黃嫚

(中交第一公路勘察設計研究院有限公司， 陜西 西安710075)

摘要：準確預測隧道涌水量能有效減少隧道病害，保護生態環境，科學指導隧道的設計與施工，而如何正確選擇和應用預測方法，是準確預測的前提條件。通過廣泛調研，在總結分析各類涌水量預測方法的原理和適用范圍基礎上，以六盤山隧道某斷面為例，深入探討了圍巖滲透系數、洞室尺寸、地下水位凈高變化、注漿圈厚度、注漿水平和襯砌抗滲等級等因素對隧道涌水量的影響，重點指出各類解析方法的局限性和適用條件，突出了注漿水平在實際工程中的作用，并建議山嶺公路隧道襯砌抗滲等級不宜小于S8。

關鍵詞：隧道涌水量； 地下水動力學； 注漿； 抗滲等級； 預測方法

0引言

涌水量是隧道動態設計信息化施工的關鍵參數，同時也是隧道修建對區域環境影響評價的關鍵因素之一。目前,我國已建、在建的隧道均存在不同程度的涌水和滲漏水問題。鑒于隧道地下水問題的重要性，國內外學者對隧道地下水涌水量問題進行了大量研究。王曉明等[1]采用降水入滲法，結合蒙特卡洛隨機模擬技術，對河北省水峪隧道的涌水量進行概率研究，為隧道涌水量預測提供了一種概率分析方法；陳冬等[2]試用SWMM模型，模擬以管道為主的巖溶隧洞涌水過程，分析SWMM模型對巖溶隧道涌水量動態變化模擬的適用性；王建宇[3]從地下水的滲流作用出發對作用于隧道襯砌的水壓力荷載的計算進行了討論，著重指出了不同水頭高度情況下水壓力的折減方法和排導系統的設置方式；喻成云[4]通過收集隧道實際涌突水樣本數量，從數學統計的角度分析隧道涌突水量的主要影響因素，并從統計角度建立了回歸方程；肖智興等[5]使用遺傳算法優化BP神經網絡的初始權值和閾值，建立了水下隧道涌水量的遺傳-神經網絡預測模型，并進行了計算分析。從調研的成果不難發現，很多學者針對某一種涌水量預測方法研究的比較深入、透徹，但缺少預測方法之間橫向、定量的比較，本文在歸納總結常用涌水量預測方法的基礎上，重點針對影響隧道涌水量的幾個主要因素進行分類討論，詳細分析了相同水文地質條件下不同預測方法的變化規律，希望為實際應用中涌水量預測方法的選擇和有效預測提供借鑒和參考。

1隧道涌水量預測方法對比分析

1.1隧道涌水量預測方法簡介

我國自20世紀80年代起，隨著技術水平和施工要求的提高，開始對隧道涌水量的預測進行系統的研究，尤其是在90年代取得了長足的進步，從定性分析逐步轉變為定量評價與計算，而隨著計算技術的不斷發展和滲流理論的不斷完善，提出了很多新的隧道涌水量計算方法，歸納起來主要有2大類，即確定性數學模型方法和隨機性數學模型分析方法[6-9]。前者主要包括比擬法、徑流模數法、解析法等，后者主要包括灰色關聯度法、時間序列分析及頻譜分析法等，詳細分類及應用條件如表1所示。

表1　隧道涌水量計算方法分類

1.2各種預測方法適用范圍

水均衡法原理簡單明了，但預測結果偏差較大，適用于工程可行性研究階段宏觀概略地預測隧道涌水量；若初測、定測階段已逐步開展了相應的地勘工作，氣象水文地質資料詳盡，可采用地下水動力學法、降雨入滲法和水文地質比擬法預測隧道涌水量；數值計算法建立在正確的水文地質模型基礎上，是目前解決復雜條件下水文地質問題的有效方法，其計算精度主要取決于模型參數的準確性，特別適用于運營期隧道排水量的預測。

從隧道埋深、地層巖性等角度考慮，淺埋隧道適合采用降雨入滲法和水文地質比擬法；深埋隧道適合采用地下水動力學法和數值計算方法；泥巖、砂巖等均質圍巖地區適合采用水文地質比擬法和地下水動力學法；巖溶區隧道或地下水系發育的地區適合采用隨機性數學模型分析方法和地下徑流模數法等方法綜合預測。

2地下水動力學法預測隧道涌水量影響因素分析

2.1地下水動力學法預測隧道最大涌水量

隧道涌水量預測通常包括正常涌水量預測和最大涌水量預測。正常涌水量是指隧道的涌水達到大致穩定時的涌水量，最大涌水量是指隧道在含水體中掘進時的峰值涌水量。預測隧道涌水量是隧道工程建設的重要內容之一，而地下水動力學法理論成熟，原理簡單，推導方便，相對于隨機性數學模型分析方法或數值計算方法，現場勘察和計算工作量較少，便于應用，是宏觀研究山嶺公路隧道涌水量控制的有效方法之一，也是高速公路隧道工程地質勘察中最常用的方法。其簡化模型如圖1所示。

隧道最大涌水量常用計算公式有以下幾種[10-13]：

1) Goodman(1965)

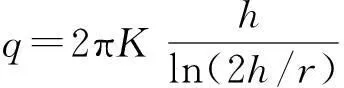
(1)

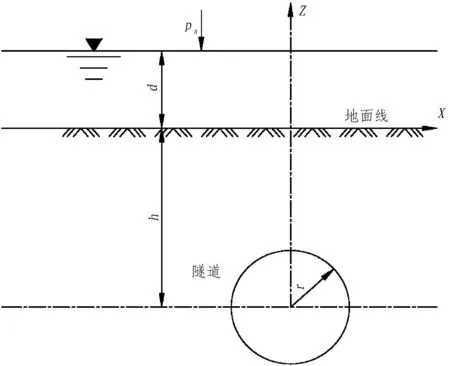
h—隧道中心到地下水位線的距離；r—隧道半徑；pa—大氣壓力水頭，一般pa=0； d—地表水深度，若無地表水，則d=0。

圖1計算模型簡圖

Fig. 1Computation model diagram

2)karlsrud (2001)

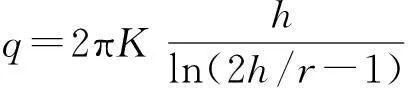
(2)

3)Lei(1999)

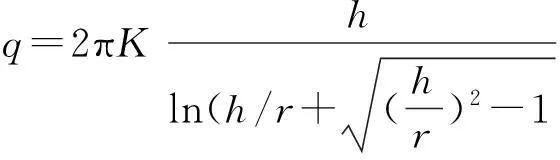
(3)

4)Lombardi(2002)

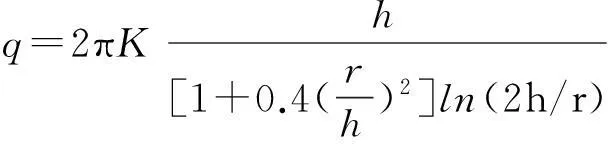
(4)

5)均質解析解

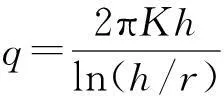
(5)

6)EI Tani(2003)

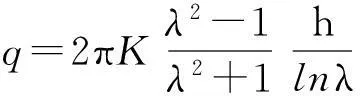
(6)

7)佐藤邦明

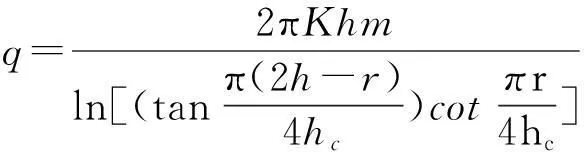
(7)

式中：m為換算系數，一般取0.86；hc為含水層厚度。

8)大島洋志公式

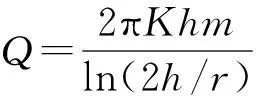
(8)

比較式(1)和式(8)可知，大島洋志預測隧道涌水量的公式增加了一個經驗修正系數m(m=0.86)，以綜合考慮實際工程水文地質邊界條件的復雜性和不確定性。

9)朱大力公式

TB 10049—2004《鐵路工程水文地質勘察規程》根據工程實例總結出預測隧道最大涌水量的經驗公式

q0=0.025 5+1.922 4 K×H。

(9)

式中H為含水層中原始靜水位到隧道底板的距離。

上述預測隧道最大涌水量公式可概括為3個類型，經典解析解，式(1)—(6)；半理論半經驗公式，式(7)和(8)；純經驗公式，式(9)。式(1)—(8)公式組成結構類似，推導原理相似，均可概括為

q0=2πmKh·f(h,r)。

(10)

式中f(h,r)為h、r的函數[14]，表達式不同，取值不同，可理解為原靜止地下水位的折減系數。

2.2隧道最大涌水量影響因素比較分析

從式(10)可以看出，地下水動力學解析解預測隧道涌水量的因素主要有圍巖滲透系數、地下靜止水位高度和洞室尺寸3種，為比較分析這3種因素在預測隧道涌水量中的作用和變化規律，以六盤山隧道某斷面為例，等效圓半徑為5.85 m，滲透系數3.20×10-7m/s，隧道埋深為200 m，計算若無特殊說明上述參數均保持定值不變。

2.2.1圍巖滲透系數

圍巖滲透系數是隧道涌水量預測的重要參數，施工現場一般通過地質鉆孔抽水試驗獲取。在地下水位高度、洞室尺寸不變的情況下，隧道涌水量隨圍巖滲透系數變化曲線如圖2所示。從圖2可以看出朱大力經驗公式預測值最大，地下水動力學經典理論解析解預測值居中，其中，除均質解析解預測值稍大外，其他解析解預測值基本相同；大島洋志公式在Goodman公式的基礎上考慮了經驗系數m=0.86，實則是對Goodman公式的折減；佐藤邦明公式除了考慮經驗系數m，還考慮了含水層厚度的影響，預測值最小。

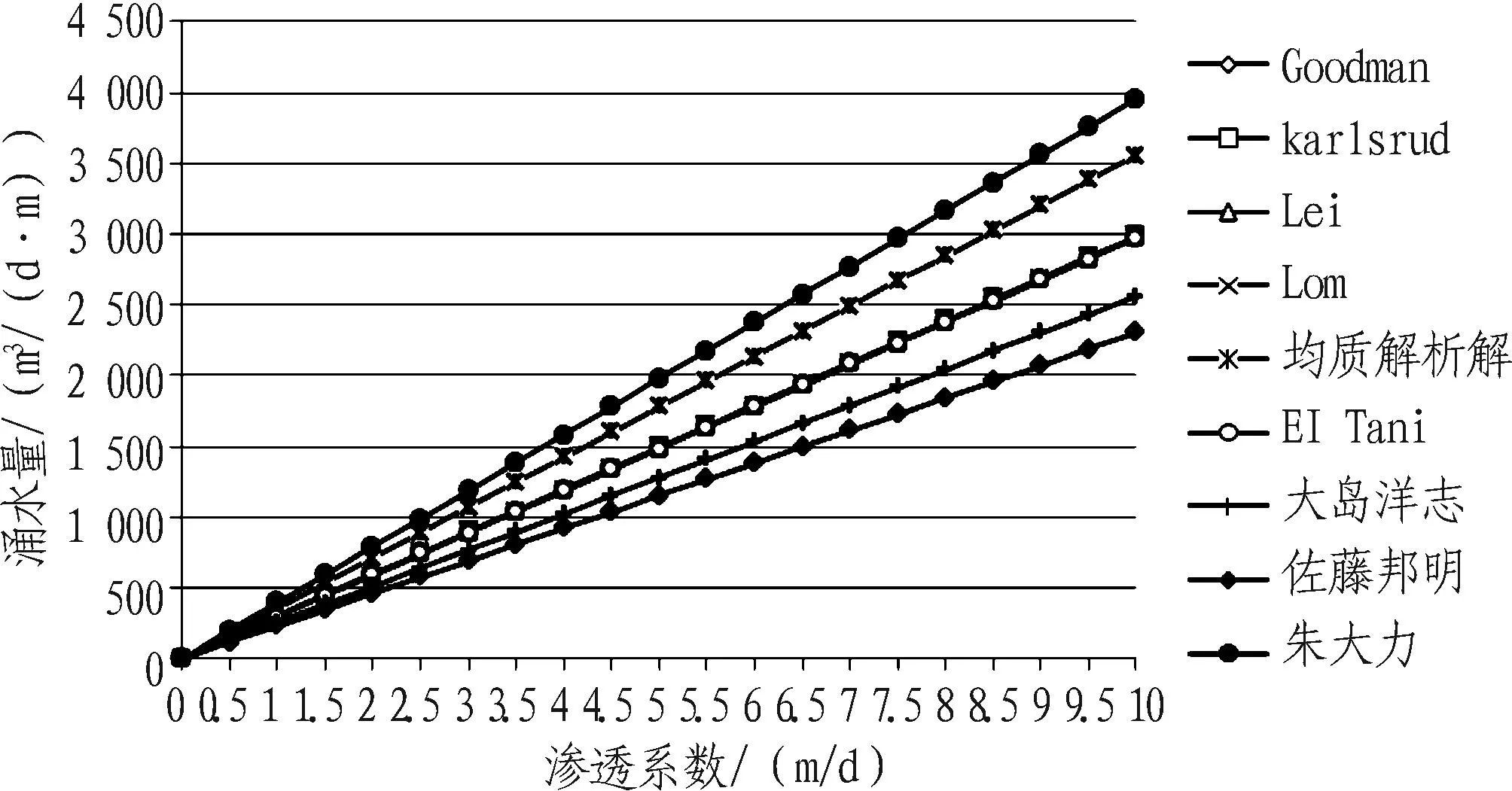
圖2　涌水量隨滲透系數變化曲線

2.2.2洞室尺寸

在圍巖滲透系數和地下水位高度不變的情況下，隧道涌水量隨洞室尺寸變化情況如圖3所示。除朱大力公式外，其他公式預測隧道涌水量隨洞室尺寸增大而增大，變化趨勢基本相同，當隧道洞徑小于5 m時，變化曲率較大，大于5 m時，變化趨勢逐漸平緩。朱大力公式預測值基本不隨洞徑尺寸變化，這與該公式的計算參數有較大關系，僅在H(原始靜水位到隧道底板的距離)中考慮了洞室尺寸效應，因一般情況下隧道半徑遠小于H，故其預測值隨洞室尺寸變化不明顯，且在洞徑尺寸較小時，預測值明顯偏大。

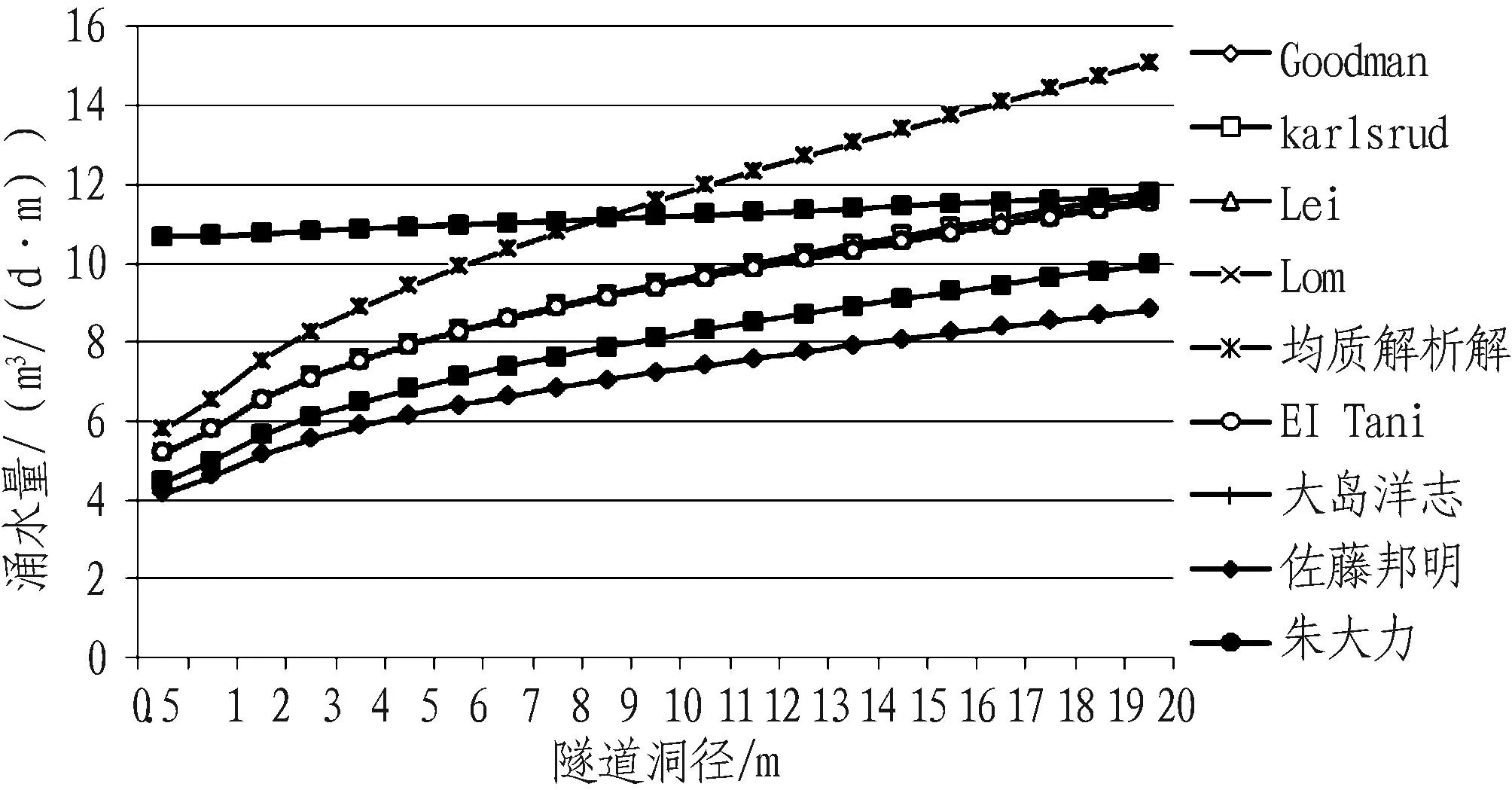
圖3　涌水量隨洞室尺寸變化曲線

除經驗公式外，同一洞徑尺寸各公式預測隧道涌水量大小關系與圖2所示規律基本一致，均質解析解預測值最大，佐藤邦明最小。

2.2.3地下水位凈高變化

地下水位凈高是指地下穩定水位面到隧道中心的距離，在圍巖滲透系數和洞室尺寸不變的情況下，隧道涌水量隨地下水位凈高變化曲線如圖4所示。從圖4可以看出，隧道涌水量隨地下水位的增加出現一個先減小后增大的過程，即存在一特定水位凈高，可使隧道涌水量最小，按本例計算參數，這一水位凈高約為10 m。在地下水位凈高較小時，均質解析解預測值偏大，其他理論解析解居中，隨著水位的不斷增加，均質解析解預測值與經驗公式預測值擬合度較高，其他理論解析解和半理論半經驗解析解預測值偏小。

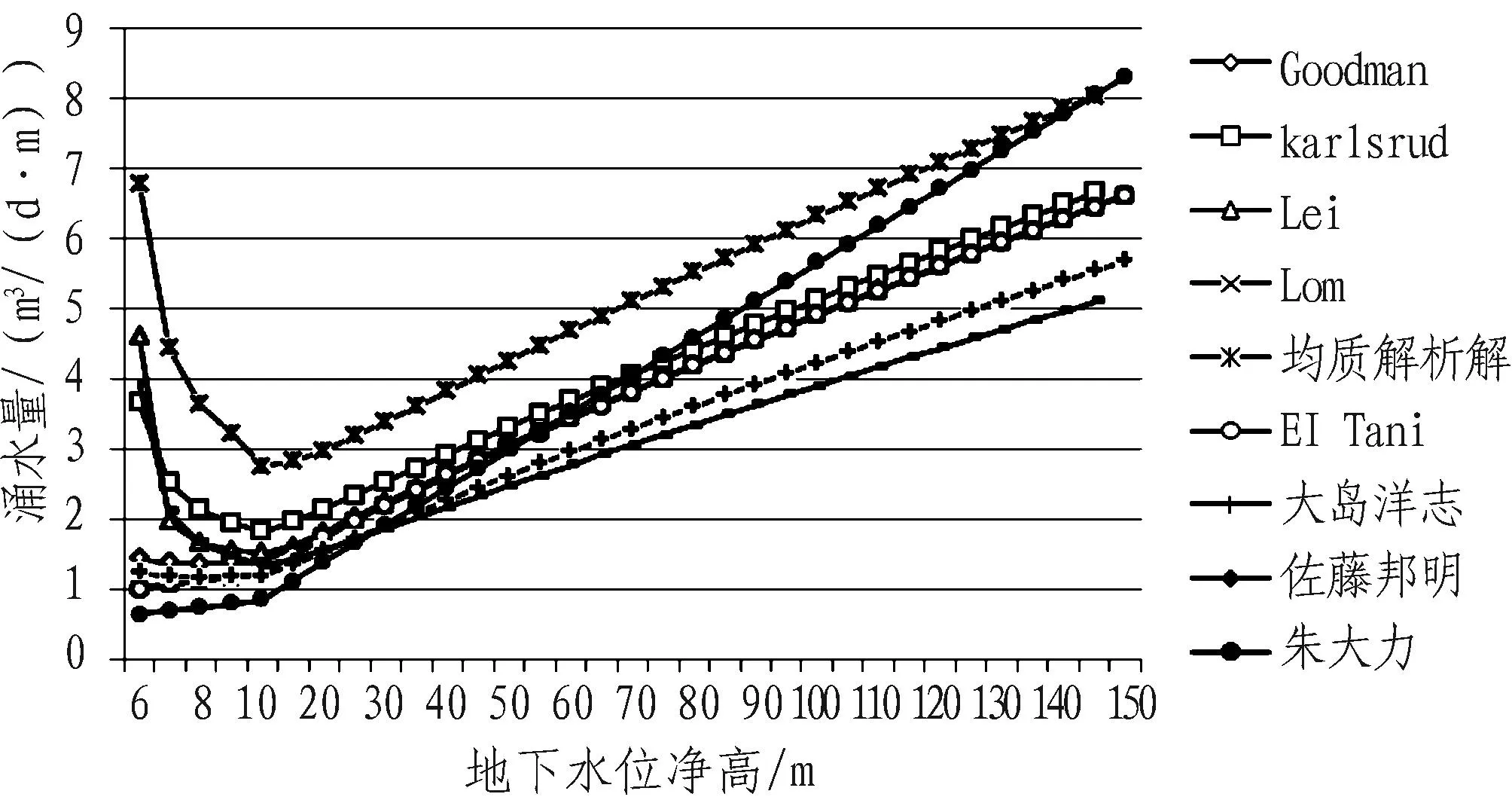
圖4　涌水量隨地下水位高度變化曲線

綜合以上隧道涌水量預測與各因素的變化規律，經典理論解析解(Goodman、karlsrud、Lei、Lom、EI Tanis)適用于地下水位凈高較小時涌水量預測，當水位凈高較大時預測結果偏小；均質解析解適用于高水位隧道涌水量預測，當水位較低時預測結果偏大；在應用朱大力經驗公式時，應注意洞室尺寸規模，當尺寸較小時預測結果偏大；半理論半經驗公式(大島洋志、佐藤邦明)折減系數m=0.86，預測結果相對偏小，可做為上述方法的對比和補充。

3洞周注漿技術及襯砌抗滲等級對隧道涌水量的影響

除地層巖性、地質構造及地下水位等地理地質因素外，隧道施工本身，如施工方案、襯砌參數等也會對隧道涌水量的大小產生影響，其中，洞周注漿技術及襯砌抗滲性能是影響最顯著的因素，高水位地區多采用增設注漿圈的方法來降低襯砌外水壓力，控制地下排水量；而襯砌抗滲等級的選擇更顯“隨意”性，缺少必要的設計依據，本節主要針對隧道施工過程中該2種因素對隧道涌水量的影響展開論述。

3.1洞周注漿技術對隧道涌水量的影響

一般而言，作用在隧道上的水荷載是滲流產生的體積力，需要通過對實際地層進行滲流場分析才能確定作用在襯砌上的水荷載以及隧道的排水量。假定圍巖為均質各向同性連續介質，王秀英等[15]提出了一種新型隧道涌水量計算方法，假設隧道為圓形，地下水頭很高，設為H，水流為穩定流，其運動規律服從達西定律。r0為襯砌內徑；r1為襯砌外徑；rg為注漿圈半徑；r2為遠場距離，等于H，計算簡圖如圖5所示。

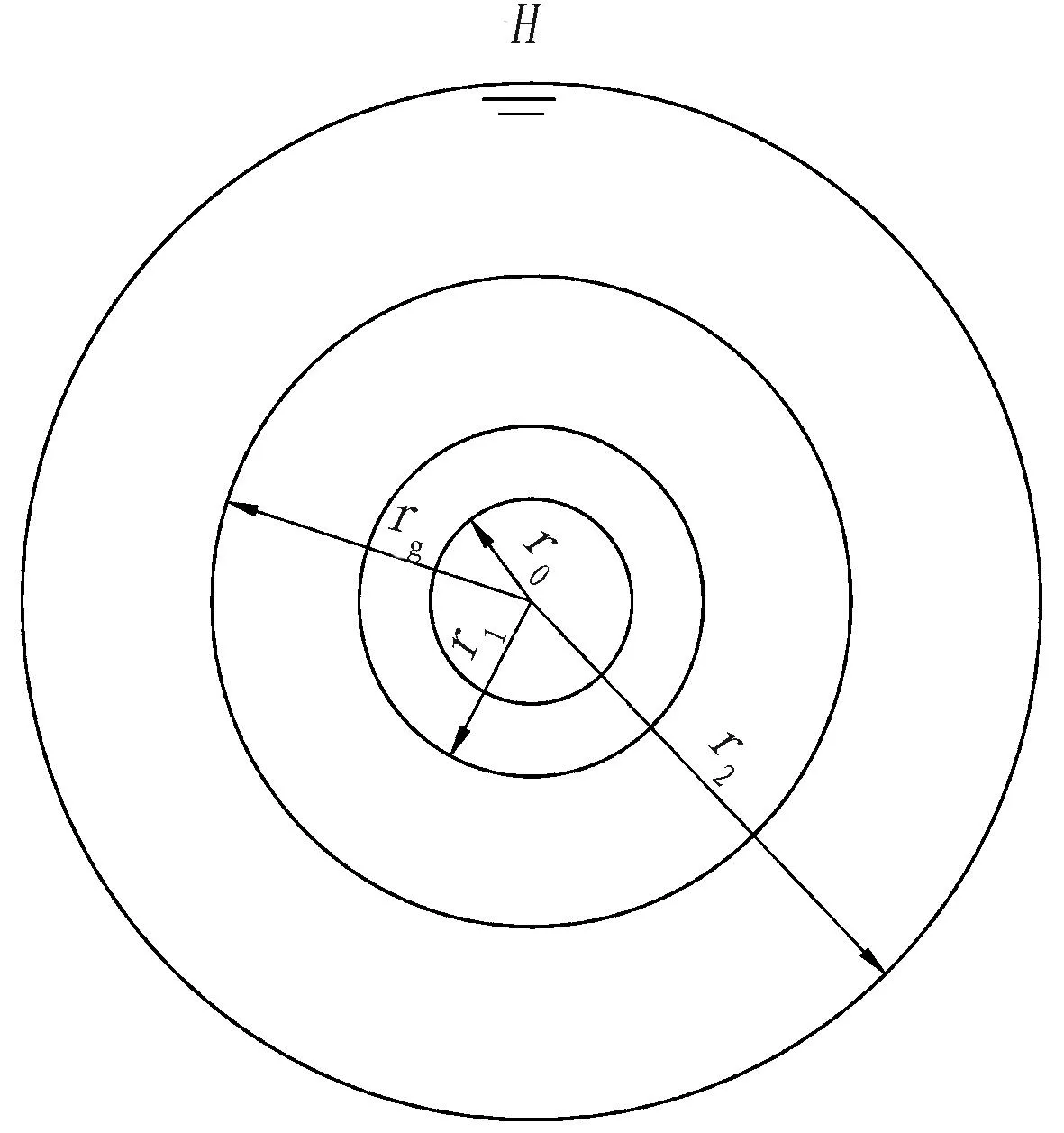
圖5　隧道涌水量計算簡化模型

根據滲流連續性方程(即Laplace方程)，可推導得出未注漿情況下每延米隧道涌水量

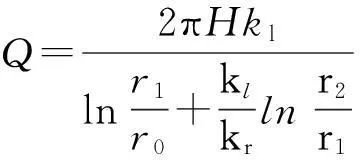
(11)

有注漿止水帷幕的情況下每延米隧道涌水量

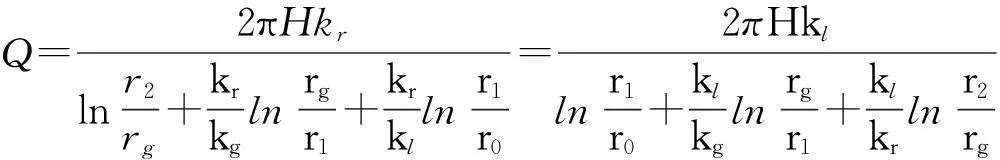
(12)

式中：kl為襯砌滲透系數；kg為注漿體滲透系數；kr為圍巖滲透系數。

由上述公式可知，隧道涌水量不僅與注漿圈厚度密切相關，還與圍巖和注漿圈滲透系數的比值、地下水位高度等條件有關。現以六盤山隧道最高水位斷面為例，應用式(12)分析圍巖注漿條件下隧道涌水量的變化規律。

1)不同注漿圈厚度與隧道涌水量的關系如圖6所示，隧道涌水量隨著注漿圈厚度的增大而逐漸減小，在相同注漿效果情況下，當注漿圈厚度≤10 m時，隧道涌水量隨注漿圈厚度的增加明顯減小，當注漿圈厚度>10 m時減小趨勢變緩，說明注漿水平和注漿圈厚度均存在一個經濟合理的范圍，不能盲目地通過增加注漿圈厚度來減少隧道涌水量。

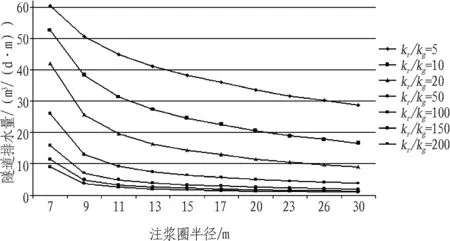
圖6　注漿圈厚度與隧道涌水量的關系

2)注漿效果與隧道涌水量的關系如圖7所示，在相同注漿圈厚度Lq的條件下，隨著kr/kg的增大(即注漿效果的提高)，隧道排水量逐漸降低。若設定隧道涌水量小于5 m3/(d·m)，當注漿圈厚度為3 m時，kr/kg需大于200；當注漿圈厚度為5 m時，kr/kg需大于115；當注漿圈厚度為7 m時，kr/kg需大于85。注漿圈厚度越小，要求注漿圈的滲透系數越小，即注漿效果更好，而相對于增加注漿圈厚度，進一步提高注漿水平來控制隧道涌水量更合理、經濟。

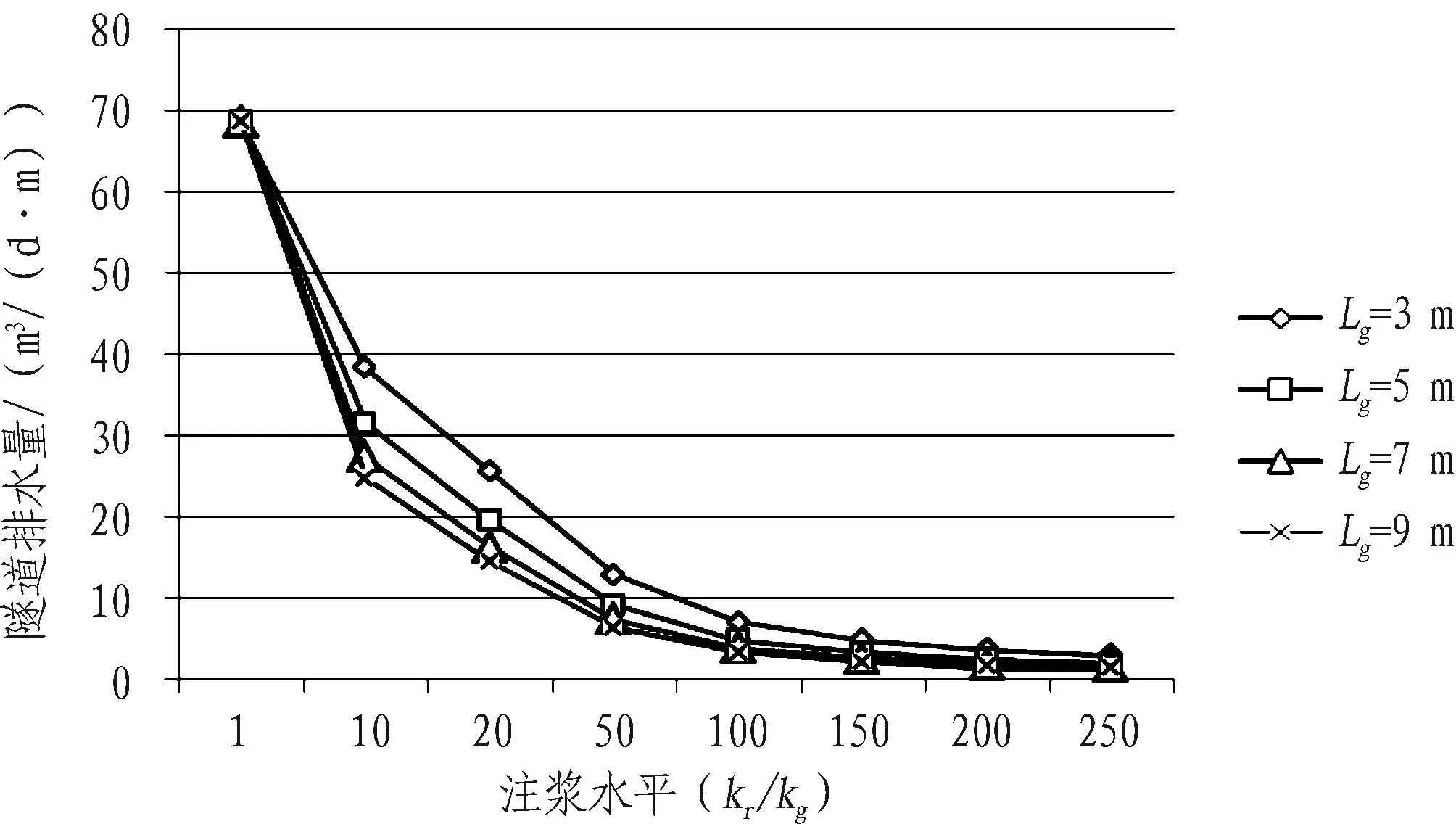
圖7　注漿水平(kr/kg)與隧道涌水量的關系

3.2襯砌抗滲等級對隧道涌水量的影響

襯砌結構是隧道防排水體系中的重要一環，同時兼顧承載、安全和防水的目的，其施工質量和抗滲性能直接關系到后期隧道運營安全。目前，山區高速公路隧道設計中襯砌抗滲等級多采用S6，部分項目采用S8，主要依據隧址區地下水位高度和圍巖滲透性能來定，本節通過數值計算方法建立了隧道涌水量與襯砌抗滲等級的關系曲線，如圖8所示，表2為各抗滲等級混凝土對應的滲透系數。

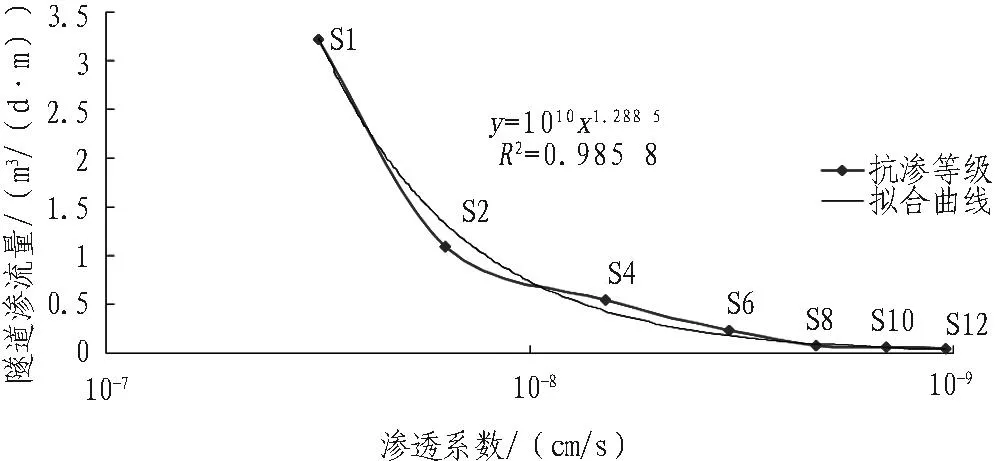
圖8　隧道涌水量與襯砌滲透系數的關系曲線

Table 2Impermeability grade and permeability coefficient of tunnel lining

滲透等級滲流系數/(cm/s)隧道滲流量/(m3/(d·m))S10.32×10-73.219S20.16×10-71.095S40.66×10-80.554S60.34×10-80.234S80.21×10-80.077S100.14×10-80.056S120.10×10-80.041

由圖8可以看出，隨著襯砌抗滲等級的提高，隧道涌水量逐步減少，當襯砌抗滲等級由S1提高到S8時，隧道的涌水量顯著減少，減小量達97.61%；而當抗滲等級由S8提高到S10、S12時，減小量分別為0.66%、1.1%，抗滲等級超過S8之后，隧道涌水量減小程度明顯變緩，逐漸趨于平穩，綜合目前我國施工技術水平及環境保護的需求，建議山嶺公路隧道襯砌抗滲等級不宜小于S8，同時在混凝土凝膠材料中可摻入CMA抗裂劑等摻料25～30 kg/m3，以進一步提高襯砌的自防水能力和結構的耐久性。

4結論與體會

1)預測隧道最大涌水量的方法可概括為以下3個類型： 地下水動力學經典理論解析解、半理論半經驗公式和純經驗公式。經典理論解析解適用于地下水位凈高較小時涌水量預測；純經驗公式不能考慮洞室尺寸的效應，斷面較小時預測結果偏大；半理論半經驗公式存在折減系數，預測結果相對偏小。

2)隧道涌水量隨著注漿圈厚度的增大及注漿水平的提高逐步減小，注漿水平和注漿圈厚度均存在一個經濟合理的范圍，不能盲目地通過增加注漿圈厚度來減少隧道涌水量，而相對于增加注漿圈厚度，進一步提高注漿水平來控制隧道涌水量更合理、經濟。

3)建議山嶺公路隧道襯砌抗滲等級不宜小于S8，同時在混凝土凝膠材料中可摻入CMA抗裂劑，進一步提高襯砌抗滲性、抗裂性和耐久性。

由于山嶺隧道地下水運動規律復雜，涌水量預測應根據項目具體的工程地質條件、地形地貌特征和水文邊界條件有針對性地選擇，目前較為常用的是確定性數學模型方法，隨機性方法涉及因素多，計算復雜，一般做為確定性方法的補充和驗證。但各種預測方法就實際應用情況來看，預測精度還遠遠不夠，特別是針對運營期隧道排水量的預測還有待進一步研究。

參考文獻(References)：

[1]王曉明，曹正波.基于水均衡方法的隧道涌水量概率預測[J].交通標準化,2014, 42(23): 112-114,118.(WANG Xiaoming,CAO Zhengbo. Probabilistic prediction of water inflow into a tunnel using water balance method[J]. Transportation Standardization,2014, 42(23): 112-114,118.(in Chinese))

[2]陳冬，許模，曾科，等. SWMM模型模擬巖溶隧道涌水量的動態變化過程分析： 以中壩隧道為例[J].地下水,2014, 36(1): 82-84.(CHEN Dong,XU Mo,ZENG Ke,et al. SWMM model to simulate the dynamic process analysis of karst tunnel water inflow[J].Ground Water，2014,36(1): 82-84.(in Chinese))

[3]王建宇.對隧道襯砌水壓力荷載的討論[J].現代隧道技術,2006(增刊)： 67-73.(WAGN Jianyu.The discussion about water pressure load on the tunnel lining [J]. Modern Tunnelling Technology, 2006(S): 67-73.(in Chinese))

[4]喻成云.基于統計分析的西南巖溶區隧道涌水量預測探析[D].成都: 成都理工大學,2013.(YU Chengyun. Based on statistical analysis of southwest China karst tunnel inflow forecast analysis[D]. Chengdu: Chengdu University of Technology, 2013.(in Chinese))

[5]肖智興,黃濤,李政,等. 遺傳-神經網絡算法在水下隧道涌水量預測中的應用[J].水資源與水工程學報,2011, 22(3): 102-105.(XIAO Zhixing,HUANG Tao,LI Zheng,et al. Application of genetic-neural network algorithm to forecast water inflow in underwater tunnel [J]. Journal of Water Resources & Water Engineering, 2011, 22(3): 102-105.(in Chinese))

[6]田海濤,董益華,王延輝.隧道涌水量預測的研究[J].水利與建筑工程學報,2007, 5(3): 75-77,97.(TIAN Haitao,DONG Yihua,WANG Yanhui. Study on forecasting for water-gushed yield of tunnel[J]. Journal of Water Resources and Architectural Engineering, 2007, 5(3): 75-77,97.(in Chinese))

[7]姜愛民,楊輝,張明.確定性數學模型方法預測隧道涌水量研究[J].工程勘察,2012,40(6): 37-41.(JIANG Aimin,YANG Hui,ZHANG Ming. Study on deterministic mathematical model for predicting water gushing yield of tunnel [J]. Geotechnical Investigation & Surveying, 2012, 40(6): 37-41.(in Chinese))

[8]陶玉敬,彭金田,陶炳勛.隧道涌水量預測方法及其分析[J].四川建筑,2007, 27(6): 109-113.(TAO Yujing,PENG Jintian,TAO Bingxun. Tunnel water inflow forecasting methods and analysis. [J]. Sichuan Architecture,2007, 27(6): 109-113.(in Chinese))

[9]鄭黎明.隧道涌水災害預測的隨機性數學模型方法[J].西南交通大學學報,1998,33(3): 273-278.(ZHENG Liming. A stochastic mathematic method for predicting gushing water from tunnel surrounding rockmasses [J]. Journal of Southwest Jiaotong University,1998,33(3): 273-278.(in Chinese))

[10]Karlsrud K.Water control when tunneling under areas in the Oslo region[J].NFF Publication,2001,12(4): 4-27.

[11]LEI Shizhong.An analytical solution for steady flow into a tunnel[J].Ground Water,1999,37(1): 23-26.

[12]李鵬飛,張頂立,周燁.隧道涌水量的預測方法及影響因素研究[J].北京交通大學學報,2010,34(4): 11-15.(LI Pengfei,ZHANG Dingli,ZHOU Ye.Study on prediction methods and its influence factors of water inflow into tunnels[J]. Journal of Beijing Jiaotong Universety,2010,34(4): 11-15.(in Chinese))

[13]王建秀,朱合華,葉為民.隧道涌水量的預測及其工程應用[J].巖石力學與工程學報，2004,23(7): 1150-1153.(WANG Jianxiu,ZHU Hehua,YE Weimin. Forward and inverse analyses of water flow into tunnels[J].Chinese Journal of Rock Mechanics and Engineering，2004,23(7): 1150-1153.(in Chinese))

[14]袁廣祥,楊莉,李剛.解析法預測隧道可能最大涌水量的對比研究[J].華北水利水電學院學報,2013,34(6): 12-15.(YUAN Guangxiang,YANG Li,LI Gang. Contrastive research on analytical methods to predict probable maximum water yield into tunnel [J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power,2013,34(6): 12-15.(in Chinese))

[15]王秀英,王夢恕,張彌.計算隧道排水量及襯砌外水壓力的一種簡化方法[J].北方交通大學學報, 2004,28(1): 8-10.(WANG Xiuying,WANG Mengshu,ZHANG Mi. A simple method to calculate tunnel discharge and external water pressure on lining[J].Journal of Northern Jiaotong Universety, 2004,28(1): 8-10.(in Chinese))

Classification of Water Inflow Prediction Methods for

Mountain-crossing Tunnels and Analysis on Related Factors

GU Boyuan, SHI Baotong, HUANG Man

(CCCCFirstHighwayConsultantsCo.,Ltd.,Xi’an710075,Shaanxi,China)

Abstract:The accurate prediction of the tunnel water inflow is helpful in minimizing the tunnel disease, protecting the environment and guiding the design and construction of the tunnel. However, the selection of proper water inflow prediction method, as well as its proper application, is a prerequisite for the accurate prediction of the water inflow. In the paper, the principles and application scopes of various water inflow prediction methods are summarized and analyzed, and the influence of the surrounding rock permeability coefficient, tunnel dimension, groundwater level, grouting ring thickness, grouting effect and lining impermeability grade on the water inflow is analyzed, with Liupanshan tunnel as an example. Furthermore, the limitations and application scopes of the analytical methods are provided, the application of the grouting effect in the water inflow prediction is highlighted, and it is proposed that the impermeability grade of the lining of mountain-crossing highway tunnels should not be inferior to S8.

Keywords:tunnel water inflow; groundwater dynamics; grouting; impermeability grade；prediction methods

中圖分類號：U 45

文獻標志碼：A

文章編號：1672-741X(2015)12-1258-06

DOI:10.3973/j.issn.1672-741X.2015.12.004

作者簡介：第一 顧博淵(1981—)，男，上海崇明人，2003年畢業于同濟大學，隧道及地下工程專業，碩士，高級工程師，現從事高速公路隧道設計工作。

收稿日期：2015-03-30; 修回日期: 2015-05-13