基于ASIFT道路交通標志的定位與識別方法*

焦再強，呂玉祥，馬維青，趙曉龍，李孟春*

(1.太原理工大學物理與光電工程學院，太原030024; 2.陽泉供電分公司，山西陽泉045000)

?

基于ASIFT道路交通標志的定位與識別方法*

焦再強1，呂玉祥1，馬維青2，趙曉龍2，李孟春1*

(1.太原理工大學物理與光電工程學院，太原030024; 2.陽泉供電分公司，山西陽泉045000)

摘要:針對智能交通系統中的交通標志識別，提出了一種基于ASIFT(仿射尺度不變特征變換)算法的定位與識別方法。首先，分類道路交通標志并提取模板;然后，采用ASIFT算法選擇目標圖像對應的模板和交通標志集合;其次，根據匹配模板ASIFT特征點的幾何分布，定位交通標志的目標區域;最后，計算目標區域和交通標志集合的特征向量歐氏距離。基于ASIFT算法，達到了準確的定位與識別效果。通過實驗，驗證了該方法的可行性。

關鍵詞:仿射尺度不變特征變換;交通標志;定位;識別

項目來源:國家自然科學基金項目(61274089)

隨著城市化進程的推進，道路交通安全和運輸效率問題日益突出。作為解決道路交通問題的重要方案，智能交通系統ITS(Intelligent Transport System)應運而生。在ITS中，交通標志識別是一個重要的技術環節，由于應用環境復雜，目前尚不成熟［1］。而交通標志傳遞的豐富信息對于規范交通運行，確保道路安全以及提高運輸效率有著重要作用。因此，交通標志識別成為了當前的研究熱點。交通標志識別分為定位與識別兩個部分，而定位與識別又相輔相成。鑒于此，本文提出了一種基于ASIFT算法［2］的定位與識別方法。借助ASIFT算法良好的仿射不變性，該方法在一定程度上克服了光照，噪聲以及視覺條件的影響，達到了較好的定位與識別效果。

1　ASIFT仿射不變性

David Lowe于1999年提出了SIFT(尺度不變特征變換)算法，并于2004年作了進一步的完善總結［3］。SIFT算法對圖像間的平移、旋轉和尺度縮放［4］保持了良好的匹配能力。Yu和Morel在SIFT算法的基礎上，于2009年提出了ASIFT(仿射尺度不變特征變換)算法。ASIFT算法保留了SIFT對平移、旋轉和尺度縮放的特征提取方法，增加了空間描述參量經度角和緯度角的特征提取［2］。因此，在繼承SIFT算法優點的同時，ASIFT算法對視角角度也具有完全不變性［2］。

2　交通標志的定位

基于ASIFT算法的交通標志定位過程可以描述如下: (1)模板與目標ASIFT特征匹配; (2)交通標志幾何定位; (3)交通標志ROI提取。

2.1模板與目標ASIFT特征匹配

為了減少ASIFT特征匹配過程中的計算量，首先對GB 5768.2—2009文件公布的道路交通標志進行分類并提取模板。以禁令標志為例，可以得到如圖1(a)所示的10個模板。對應每個模板，均有一個交通標志集合與之對應，圖1(b)中顯示了bm1模板及其對應集合中的部分交通標志圖像。

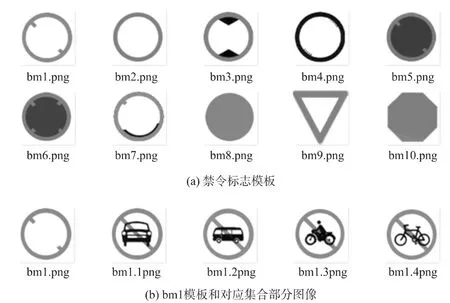
圖1　

采用ASIFT算法對模板和目標圖像進行特征點匹配［5］，并從匹配結果中選擇匹配程度最優的一個模板。根據該模板的信息，確定目標圖像所含交通標志對應的集合;同時，記錄特征點在該模板和目標圖像中的像素坐標分布［5］。

2.2交通標志幾何定位

根據特征點的像素坐標分布和模板及目標圖像的特征點仿射關系，理論上能夠計算出交通標志的外輪廓。但是，受ASIFT算法對特征點識別率的影響，特征點的仿射關系會發生小概率錯誤。錯誤的仿射關系給最終的計算結果造成了較大的誤差，使計算趨于發散。

針對上述情況，本文提出了一種新的定位方法來解決上述問題。該方法首先統計并提取特征點較為密集的區域，然后計算各個區域的重心坐標。假設密集區域A包含N個特征點，第i(0＜i＜N+1)個特征點的像素坐標為(xi，yi)，區域A重心坐標G(x，y)的計算方式如下:

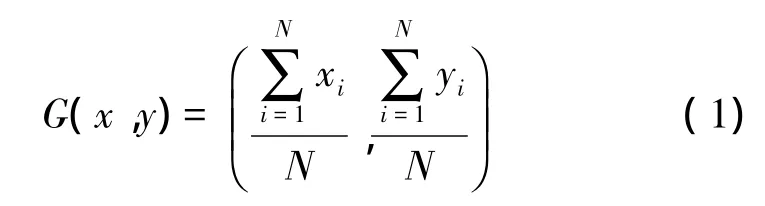
通過上述方法，在模板中，計算得到特征點密集區域的重心坐標序列。同理，從目標圖像對應的特征點密集區域中，計算得到對應的重心坐標序列。在模板的重心坐標序列中，根據如下兩個條件選取3個重心點:?三個重心點非共線;?任意兩個重心點的連線與模板邊界相交。

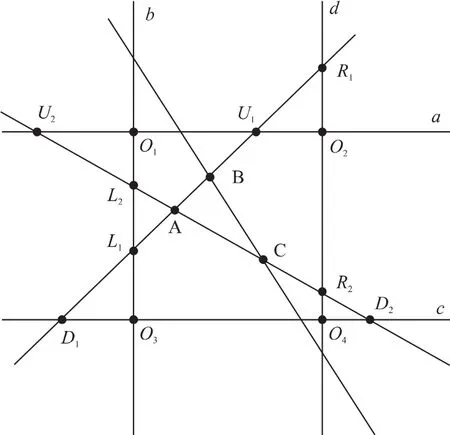
圖2　模板幾何圖

如圖2所示，設選取的非共線重心點及坐標分別為A(xA，yA)，B(xB，yB)，C(xC，yC)，模板圖像的4個頂點及坐標分別為O1(XL，YU)、O2(XR，YU)、O3(XL，YD)、O4(XR，YD)，通過模板4個邊的直線分別記作a，b，c，d。根據A、B、C 3個點的選取條件，直線AB與直線a，直線b，直線c，直線d分別相交于點U1、點L1、點D1、點R1;直線AC分別與直線a、直線b、直線c、直線d相交于點U2、點L2、點D2、點R2。8個向量分別滿足下列公式:

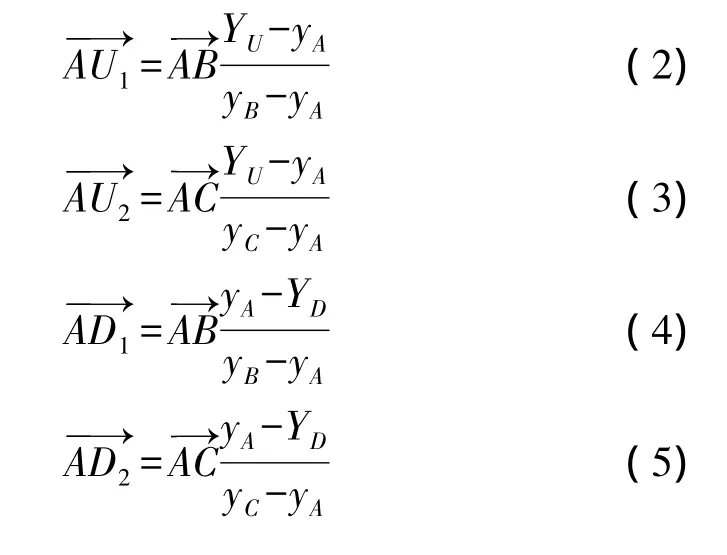
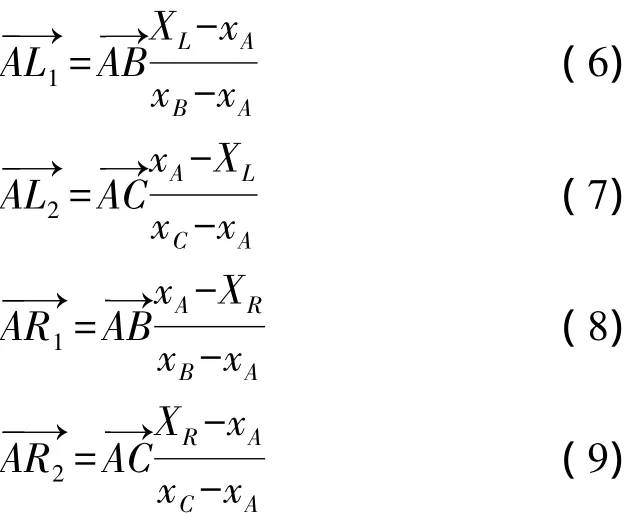
由于8個點(U1，U2，L1，L2，D1，D2，R1和R2)的坐標確定了模板的4條邊: a，b，c，d，因此可以確定模板的輪廓。同理，將目標圖像中與之對應的8個點設為:，根據仿射關系，則可以通過對應8個點的坐標確定目標區域的輪廓。

如圖3所示，從目標圖像的重心坐標序列中選取與A、B、C 3點對應的3個重心點: A'(xA'，yA')，B'(xB'，yB')，C'(xC'，yC')。根據模板與目標圖像的仿射關系，8個向量分別滿足下列公式:

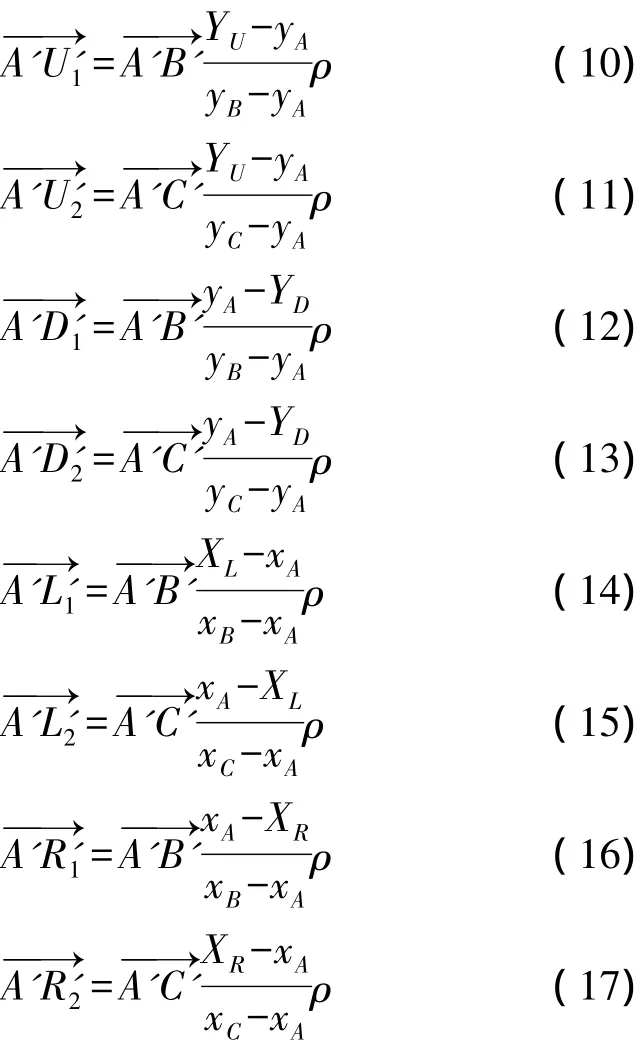
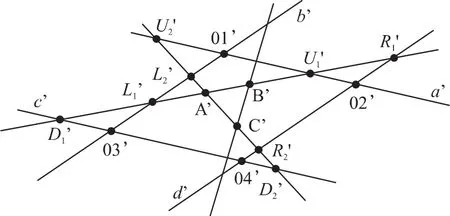
圖3　目標圖像幾何圖

在上述公式中，修正因子ρ∈［1，∞)。在實際應用中，離散的數據源會引入計算誤差;成像透視變形會導致特征點對應的比例失真;同時，其他的因素也會帶來一定的誤差。這些誤差會導致對目標區域定位的非完整性。引入修正因子ρ后，可適當調整選取范圍，以完整定位目標區域。通過以上8個公式，可以計算得到8個點()的坐標，從而確定目標區域的4條邊: a'，b'，c'，d'，進而確定目標區域的輪廓:

2.3交通標志ROI提取

3　交通標志的識別

模板與目標圖像的ASIFT特征匹配確定了ROI所含交通標志的集合信息。在集合范圍內，進一步識別ROI所含交通標志的具體類型。

3.1ROI特征點檢測

在尺度空間［8］上，圖像數據包含了圖像自身的多尺度特征［9］。根據文獻［10］提出的方法，利用高斯卷積核，可將二維圖像I(x，y)的尺度空間描述如下［10－12］:

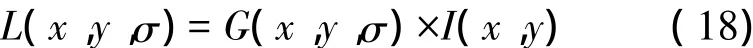
尺度可變高斯函數G(x，y，σ)定義如下［10－12］:

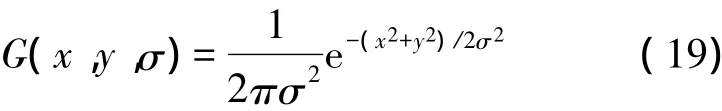
高斯差分尺度空間［13］(DOG Scale Space)利用高斯差分核與圖像進行卷積生成，DOG算子的定義如下所示［10－12］:

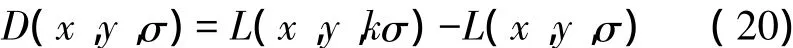
利用DOG算子將ROI圖像的采樣點和其相鄰點比較，如果該點是鄰域中的極值點，則將其判斷為一個特征點。

3.2生成特征點描述

在ROI的特征點中，對每個特征點鄰域窗口的梯度分布建立直方圖統計，選取直方圖峰值的梯度方向作為該特征點的主方向。將坐標軸旋轉至主方向，以保證特征向量的旋轉不變性。以特征點為中心選取16×16窗口，建立8個梯度方向的直方圖。將16×16窗口分為16個4×4小塊，在每個4×4小塊上，標定每個梯度方向的累加值，形成一個種子點。這樣一個特征點包含了16個種子點，每個種子點含有8個方向的向量信息。因此，每個特征點可以描述為一個128維的特征向量，該特征向量包含了鄰域方向性信息，既增強了抗噪聲能力，又對定位誤差提供了較好的容錯性［3］。

3.3特征向量匹配

將ROI所包含的圖像記作Isrc，將ROI對應集合中的任意一幅交通標志圖像記作Idst，計算Isrc特征向量與Idst特征向量的歐式距離［14］，將歐氏距離的大小作為特征點相似性的判定度量［15］。方法如下:

選取Isrc中的一個特征點，記作點M，在Idst中找出與點M特征向量歐氏距離最近的兩個特征點，最近特征點記作點T，次近特征點記作點R。計算點T與點R特征向量歐氏距離的比值，若比值小于一定的閾值，則認為點M與點T匹配成功［16］。閾值的大小與匹配個數正相關，與匹配穩定性負相關。根據最終的匹配結果，選取集合中匹配個數最多的交通標志圖像作為最終的識別結果。

4　實驗結果及算法性能分析

本節將圍繞上述算法進行實驗測試，并根據實驗結果分析上述算法的識別性能。

實驗平臺的系統配置為: Windows 7操作系統和Intel Core i3－2310M處理器。在VS2010開發環境下，實現并測試了本文中提出的交通標志定位與識別方法。

4.1測試目標選擇

為了證明上述算法具有適應光照，噪聲和旋轉變化的魯棒性，被測試目標圖像的取材條件為:光照條件下拍攝，交通標志與周圍環境輕微融合，拍攝視角傾斜。如圖4所示。

圖4　測試目標圖像

4.2模板匹配和集合確定

如圖5所示，從左至右，從上至下，分別為模板bm1、bm4、bm5、bm10與目標圖像的ASIFT特征匹配結果。從匹配結果可知，匹配程度最好的模板為bm1。

圖5　模板與目標匹配

4.3交通標志ROI定位與提取

根據2.2和2.3中的定位與提取方法，確定的3個非共線重心點如圖6(a)所示。修正因子取值1.2時，提取的交通標志ROI如圖6(b)所示。圖6(b)中，ROI的輪廓是掩碼邊界框與圖像邊界取交集的結果。

4.4交通標志識別

根據3.3中的方法，在最佳模板bm1相關集合范圍內，匹配ROI與交通標志圖像的特征向量。由于特征向量匹配涉及的數據量非常大，因此用ROI與交通標志圖像的特征點匹配來演示最終的識別效果。如圖7所示，從左至右，從上至下，分別為模板bm1集合中bm1_1、bm1_2、bm1_3、bm1_4與ROI的特征點識別結果。從識別效果中可以判斷，目標圖像中含有的交通標志為bm1_1所表示的交通標志，即禁止機動車通行標志。

圖6　

圖7　交通標志識別結果

4.5算法性能分析

為了進一步證明該算法在實際應用中的可行性，在紅色禁令標志，藍色指示標志和黃色警告標志中，隨機選取30種交通標志，并對其從不同角度拍攝取材進行實驗。將標志平面與相機光軸的夾角記作θ，拍攝角度θ的范圍為: 5°到175°，每隔5°拍攝一張，最后收集1 050張測試圖像。用經典的LDA (Linear Discriminant Analysis)算法和本文中的算法同時對1 050張測試圖像進行識別，識別結果如表1和表2所示。

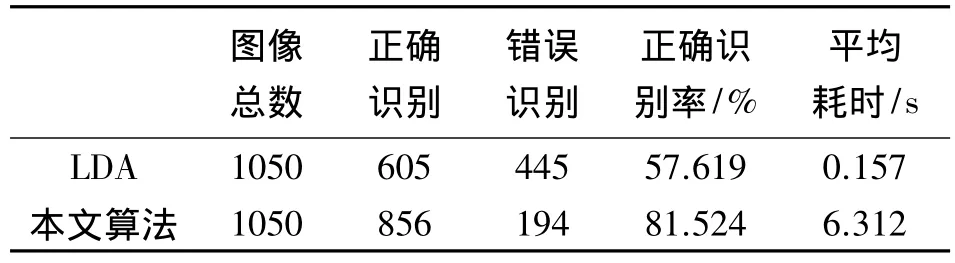
表1　兩種算法總體性能對比

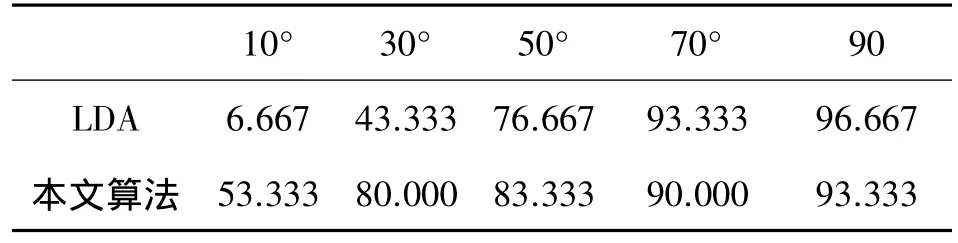
表2　兩種算法對不同角度圖像的識別率　單位: %

分析表1和表2可以得出如下結論:本文算法的總體識別率高于LDA算法，并且對圖像角度的變化適應性較強。但是，本文算法的不足之處是識別時間較長，這是由ASIFT算法中多個仿射變換匹配引起的，導致算法的時間復雜度大于LDA算法。在空間復雜度上，由于研究目的傾向于識別率的提高，所以采用128維的特征向量來描述一個特征點，產生了較大的空間復雜度。實際應用時，可對空間復雜度和識別率折衷選擇。借助專用數字信號處理器，可以在滿足識別率的同時，優化該算法的時間和空間復雜度，從而實現該算法的實際應用。

5　結束語

本文通過分析ASIFT算法的特點，提出了一種基于ASIFT算法的交通標志定位與識別方法，并通過VS2010開發環境驗證了該方法的可行性。通過實驗結果可以得出，該方法在一定程度上克服了光照，噪聲以及視覺條件的影響，達到了較好的定位與識別效果。在下一步的研究中，將結合DSP硬件平臺，對該方法中涉及的關鍵環節進行優化，以降低時間和空間復雜度，從而實現該方法在嵌入式領域的實時應用。

參考文獻:

［1］李祥熙，張航.交通標志識別研究綜述［J］.公路交通科技應用技術版，2010(6) : 253－257.

［2］Morel J M，Yu G.ASIFT: A New Framework for Fully Affine Invariant Image Comparison［J］.SIAM Journal on Imaging Sciences，2009，2(2) : 438－469.

［3］Lowe D G.Distinctive Image Features from Scale-Invariant Keypoints ［J］.International Journal of Computer Vision，2004，60(2) :91－110.

［4］鄭永斌，黃新生，豐松江.SIFT和旋轉不變LBP相結合的圖像匹配算法［J］.計算機輔助設計與圖形學學報，2010，2(2) : 286－292.

［5］蔣慶斌，王浩，趙力.基于UKF與SIFT的車輛跟蹤算法研究［J］.計算機測量與控制，2012，20(10) : 2824－2826.

［6］王鵬宇.基于小波和色彩傳遞夜視圖像彩色融合算法研究［J］.電子器件，2014，37(1) : 143－145.

［7］劉歡，郝礦榮，丁永生，等.光照魯棒的抗模糊新組合不變矩圖像匹配方法［J］.傳感技術學報，2013，26(9) : 1258－1264.

［8］傅衛平，秦川，劉佳，等.基于SIFT算法的圖像目標匹配與定位［J］.儀器儀表學報，2011，32(1) : 163－169.

［9］溫文雅.一種改進的Harris多尺度角點檢測算法［J］.重慶理工大學學報，2012，26(8) : 94－97.

［10］陳杏環，閆海煜.基于隨機游走策略改進的降雪模型圖像分割方法［J］.電子器件，2014，37(2) : 350－354.

［11］高紹雷，沈建新，周洪亞，等.高斯核函數在角膜地形圖儀圖像處理中的應用［J］.小型微型計算機系統，2011，32(10) : 2074－2077.

［12］田瑩，徐超，張一鳴.基于Gabor小波和ASIFT特征點的人耳識別［J］.計算機應用與軟件，2013，30(11) : 202－205.

［13］張良，王海麗，吳仁彪.基于改進局部不變特征的興趣點匹配［J］.電子與信息學報，2009，31(11) : 2620－2625.

［14］周強，楊智勇，孫小燕，等.基于圖像歐式距離的KPCA SAR圖像目標識別算法［J］.火力與指揮控制，2012，37(12) : 38－41.

［15］張闖，王婷婷，孫東嬌，等.基于歐式距離圖的圖像邊緣檢測［J］.中國圖象圖形學報，2013，18(2) : 176－183.

［16］唐朝偉，肖健，邵艷清，等.全局結構化SIFT描述子在圖像匹配中的應用［J］.華中科技大學學報:自然科學版，2012，40(1) : 15－20.

焦再強(1989－)，男，漢族，山西臨汾人，太原理工大學碩士研究生，主要研究方向為信息處理與微系統，jiaozaiqiang@ foxmail.com;

李孟春(1963－)，女，漢族，山西太原人，太原理工大學教師，副教授，碩士生導師，主要研究方向為光電技術，limmc163@ 163.com。

An Algorithm of Fast Video Block Motion Estimation
Based on Sub-GCK*

WANG Guan1*，LUO Shen1，GE Jia2
(1.The 28th Research Institude of China Electronics Technology Group Corporation，Nanjing 210007，China; 2.Laboratory of Image Science and Technology，Southeast University，Nanjing 210096，China)

Abstract:Fast video block motion estimation is one of the most important problems in video coding.Based on Gray Code Kernels(GCK) algorithm，the paper proposes an improved Sub Search Gray Code Kernels(Sub-GCK) algorithm，whose computational complexity reduces to 22.1% comparing to GCK.We also compare the encoding performance of new algorithms with that of GCK as well as some other common motion estimation algorithms in experiments.The results show that the proposed Sub-GCK algorithm，comparing to other ones，effectively reduces the time for motion estimation with guaranteed reasonable encoding quality.The running time of Sub-GCK algorithm is about 41.9% of original GCK algorithm.

Key words:video coding; motion estimation; sub search gray code kernels(Sub-GCK) ; computational complexity; running time

中圖分類號:TP391

文獻標識碼:A

文章編號:1005－9490(2015) 03－0693－06

收稿日期:2014－07－01修改日期: 2014－07－11

doi:EEACC: 6120B10.3969/j.issn.1005－9490.2015.03.045