貴州省典型喀斯特地區地表水系結構特征研究

李圓玥，高華端，羅忠志

(貴州大學 林學院，貴州 貴陽 550025)

貴州省典型喀斯特地區地表水系結構特征研究

李圓玥，高華端，羅忠志

(貴州大學 林學院，貴州 貴陽 550025)

喀斯特地區；水系結構；特征；貴州省

喀斯特地區地質、地形、地貌的特殊性，導致發育形成的流域水系具有自己的典型特點。為了探討喀斯特地區地表水系特征，以貴州省息烽縣典型喀斯特地區作為研究對象，運用GIS技術與地貌侵蝕循環理論，研究了貴州喀斯特地區的地表水系結構特征。研究結果表明：從水系形態上看，該地區在負地形部位發育了相當數量的星狀水系；從整個水系網的特征上看，該區發育的地表水系中低級水道數目較高級水道多，且水道平均長度較短，有大量低級地表水系向下發展匯入地下水系，其中一至四級水道均有部分水道匯入地下，形成地下水系。

喀斯特(巖溶)地區水文地貌系統與非喀斯特流域的常態流水地貌系統既有相同的一面， 如流水的侵蝕作用，又有不相同的一面，即水的溶蝕作用[1]。正是因為這種差異性，形成了喀斯特地區特有的地表地下雙層空間結構。小至溶溝、溶穴、石芽，大至溶蝕洼地、漏斗、落水洞、峰叢、峰林、溶蝕槽谷、孤峰、殘丘，喀斯特地貌對地表徑流過程構成了直接影響，致使喀斯特流域地貌形態、水道系統和分形特征等與常態流域存在較大差異，在產流、匯流、泥沙輸移等水文過程方面有其自身規律。本研究以貴州省息烽縣典型喀斯特地貌區為研究對象，定量研究其地表水系結構特征，希望能為喀斯特地區土壤侵蝕過程研究、土壤侵蝕預測預報和水土保持規劃制定提供參考。

1 研究區概況

息烽縣位于貴州省中部、烏江南岸，地理坐標為E106°27′29″—106°53′43″、N26°57′42″—27°19′45″，屬亞熱帶季風性濕潤氣候區，冬無嚴寒，夏無酷暑。碳酸鹽類巖石的分布面積為787.91 km2，占全縣總面積的76%，在地層剖面中的厚度為3 406 m，占地層總厚度的59%，無論垂直分布和水平分布均占主導地位。加上區域性的水熱條件適宜，溶蝕作用強烈，致使巖溶地貌廣泛發育，在巖溶地貌中溶丘、溶洼、漏斗、落水洞、溶洞、地下伏流等經常可見。烏江流域是西南喀斯特高原區的核心地帶，息烽縣位于烏江流域的中游，巖溶地貌極其發育。研究息烽縣地表水系結構特征有助于進一步認識貴州喀斯特地區的水系分布規律。

2 研究方法

2.1 基礎數據的提取

先對收集到的地形圖進行矢量化處理，提取縣境內的水系圖。然后對水系定級，采用Horton-Strahler水系分級原則[2]對水系進行等級劃分。具體方法是：將位于河源頂端、不再分支且具有明顯槽床的水道作為一級水道；兩條一級水道匯合后形成的新河道為二級水道；兩條二級水道匯合后形成的新河道為三級水道，以此類推。最后，統計出水系中所包含的水道級別，各級別水道的數目、總數、長度等基礎數據。

2.2 水系特征值計算

根據Horton定理[3]，水道的長度比(rl)是某級水道的平均長度與低一級水道的平均長度之比，其計算公式為

rl=Lμ/Lμ-1

(1)

式中：Lμ為某級水道的平均長度，km；Lμ-1為低一級水道的平均長度，km。

水道的分支比(rb)是某一級水道數量與比其高一級水道數量的比值，其計算公式為

rb=Nμ/Nμ+1

(2)

式中：Nμ為某一級水道數量；Nμ+1為高一級水道數量。

Horton第一定律提出在任何一個流域，不同級別的水道數目十分接近于一個遞減的幾何級數，該級數的第一項是分支比，計算公式為

Nμ=rb(s-μ)

(3)

式中：rb為分支比；s為水系最高級別；μ為某級水道級別。

水道密度和水道頻度。水道密度是水系系統中地形要素的重要指標之一，反映了水系的長度面積比[4]，它是指單位面積內水道的總長度，而水道頻度是指單位流域面積上的河流數目，其計算公式分別為

D=L/A

(4)

F=N/A

(5)

上二式中：D為水道密度，km/km2；L為水道總長度，km；A為流域面積，km2；F為水道頻度，條/km2；N為水道總數目。

3 結果與分析

根據息烽縣1 ∶5萬地形圖提取出水系圖為水系定級后，統計和計算得到最高級的水道級別為六級，共有水道6 441條，水道總長度2 847.26 km，水道頻度6.21條/km2，水道密度2.75 km/km2，各級別水道特征值見表1。

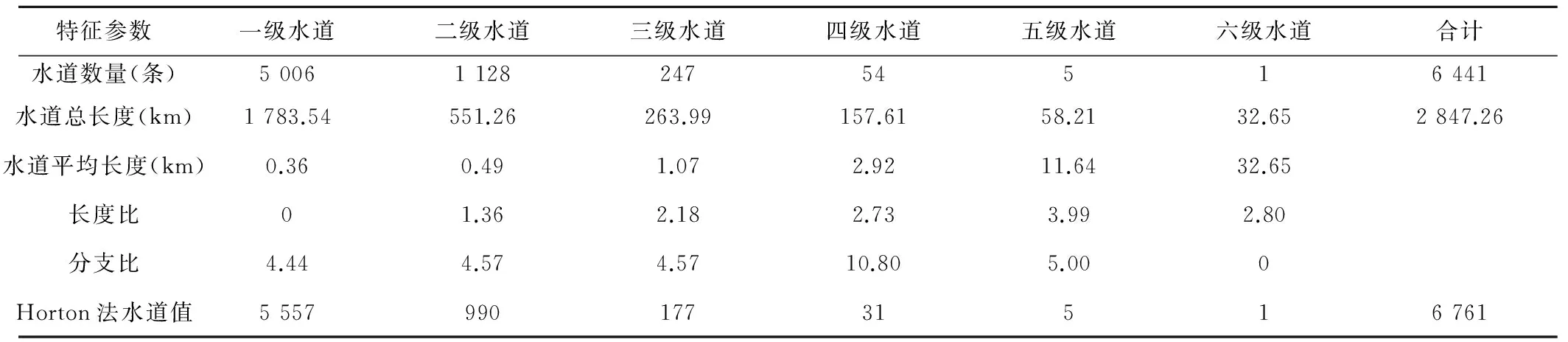
表1 息烽縣水系網特征參數

3.1 水系形狀

從水系發育的特點來看，喀斯特地區發育形成的水系不僅具有常態地貌區所發育形成的樹枝狀水系，而且也發育有喀斯特地區特有的星狀水系。星狀水系往往發生在峰叢洼地等負地形(四周高中間低)。在這種特殊的地形中，由于巖石具有溶蝕性，所以常形成落水洞或者豎井等，并與地下暗河相連，形成地表水系向地下水系轉換的通道，導致喀斯特地區地表中級水道較少，低級水道短而密，水道分支比偏大。

3.2 水道數量

根據息烽縣水系網所統計的水道數量，境內發育的最高級別水道為六級，包括一級水道5 006條、二級水道1 128條、三級水道247條、四級水道54條、五級水道5條、六級水道1條。從水系級別與各級別水道數量的關系曲線看(圖1)，隨著水道級別增加各級別水道數量逐漸減少；相比一級水道，二級水道數量急劇減少，三級水道處出現拐點，之后水道數量下降緩慢，并趨于穩定。將流域內各級水道總數求對數后與水道級別做相關性分析(圖1)，得到回歸方程為

lgNμ=-0.749 1μ+4.450 7 (R2=0.993 5)

(6)

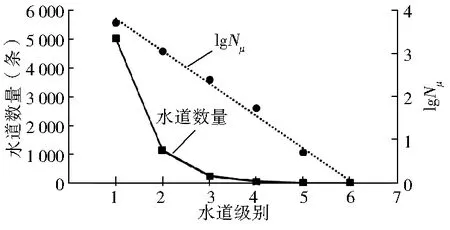
圖1 各級別水道數量及其對數與水道級別的關系

這一結果與Horton定理提出的流域內各級水道數量的對數與水道級別之間呈一遞減的線形關系的結論相吻合。對水道數量和水道級別的關系圖進行分析，可以把圖分為兩個部分(以三級水道為分界點)：前部分為一級到三級水道，水道數量隨著水道級別的遞增，呈現陡降的趨勢；后部分為三級到六級水道，水道數量隨著水道級別的遞增，呈現緩慢減少的趨勢。

3.3 水道長度

(1)水道總長度。息烽縣境內發育的水系網水道總長度為2 847.26km，其中一級水道總長度為1 783.54km，水道長度的波動區間為0.07～2.36km；二級水道551.26km，波動區間為0.02～3.57 km；三級水道263.99 km，波動區間為0.05～6.22 km；四級水道157.61 km，波動區間為0.14～12.85 km；五級水道58.21 km，波動區間為5.82～21.47 km；六級水道32.65 km。從水道級別與水道總長度的關系曲線(圖2)可以看出，隨著水道級別遞增，水道總長度逐漸減少。也可以把整個圖形分為兩個部分(以三級水系為分界點)：一級到三級水道，隨著水道級別遞增，水道總長度呈現陡降的趨勢；三級到六級水道，水道總長度呈現緩慢減少的趨勢。

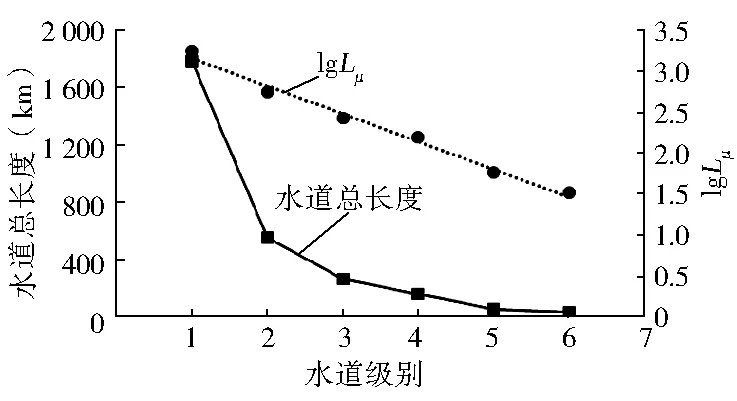
圖2 各級別水道總長度及其對數與水道級別的關系

把流域內各級水道總長度求對數后同樣地與水道級別做相關性分析，得出各級水道總長度的對數與水道級別之間呈直線關系(圖2)，回歸方程為

lgLμ= -0.338 3μ+3.499 1 (R2=0.987 6)

(7)

這一結果與A.N.Strahler根據GreatSmoky等地區的6個隨機水道的綜合資料得出各級水道總長度的對數與水道級別之間的回歸線是一條直線的結論相符。水道總長度與水道級別的變化趨勢與水道數量與水道級別的變化趨勢是一致的。原因在于，隨著水道級別增加，水道總數減少，相應的水道總長度也在減少，這種長度和數量的對應關系是一致的。

(2)水道平均長度。息烽縣境內發育的水系網中各級別水道的平均長度分別為：一級水道0.36km，二級水道0.49km，三級水道1.07km，四級水道2.92km，五級水道11.64km，六級水道32.65km。從水道級別與水道平均長度的關系曲線(圖3)可以看出，隨著水道級別遞增，水道平均長度逐漸增加，以三級水道為臨界點，即一級至三級增加緩慢，四級以后急劇增長，說明息烽縣發育的低級別水道的平均長度比較短，高級別水道的平均長度比較長。

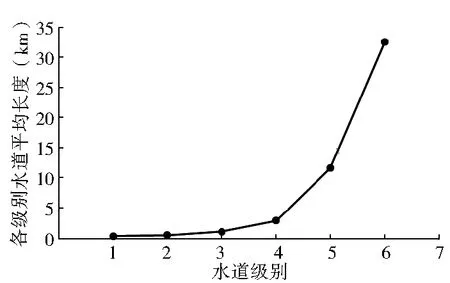
圖3 各級別水道平均長度與水道級別的關系

3.4 長度比

根據公式(1)，一級水道長度比為0，二級水道為1.36，三級水道為2.18，四級水道為2.73，五級水道為3.99，六級水道為2.80。把流域內各級水道的平均長度分別與一級水道的平均長度相除，所得的值取對數后與水道級別做相關性分析(圖4)，得出回歸方程為

lg(Lμ/L1)=0.41μ-0.604 6 (R2=0.967 7)

(8)

這一結果符合Horton第二定律提出的各級水道平均長度比與級別之間呈半對數的直線關系的結論。

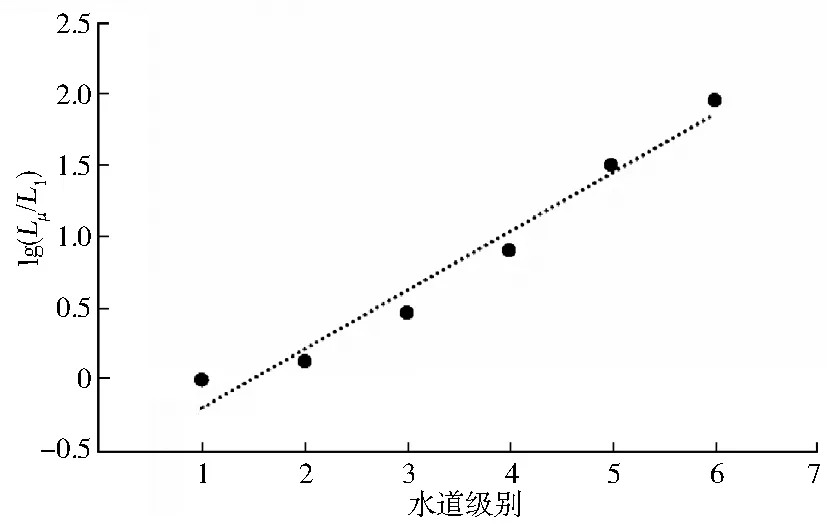
圖4 各級水道長度比與水道級別的關系

3.5 分支比

由息烽縣水系網統計資料計算出的各級水道的分支比分別為：一至二級水道4.44，二至三級水道4.75，三至四級水道4.75，四至五級水道10.80，五至六級水道5.00。Horton對流域分支比的定義是有缺陷的，因為不是所有的一級水道全部匯入二級水道，它可以直接匯入三級、四級或更高級的水道中，這一推理對于更高級的水道同樣適用，所以采用Horton方法計算出的分支比不能合理地模擬水系的形成過程。于是，K．G．Smith提出運用各級別水道總數的對數與水道級別的關系圖來推算流域的平均分支比，這種方法也被現在的研究者所引用。具體方法是將圖1中求得的回歸方程中的回歸系數b(b=-0.749 1)取反對數得到流域的平均分支比，表達式為

rb= lg-1(-0.749 1)

(9)

推算出水道分支比rb=5.61。大量研究表明，天然河網的平均分支比接近一個常數，數值變化范圍為3～5。對于平坦的或丘陵起伏的流域，分支比為2～3；多山或強烈起伏的流域，分支比為4～5或更大[4]。息烽縣的水系分支比為5.08，說明息烽縣多山且地形起伏強烈。根據Horton第一定律計算各級水道數量。將計算出的息烽縣各級水道數量與地形圖上實測的數值進行比較(圖5)，發現兩者之間是有差別的：一級水道的計算值大于實測值，而二級、三級、四級水道的計算值小于實測值。這表明用水道平均分支比計算出的水道數量與喀斯特地區發育形成的水道數量之間是有差異的，Horton方法不能切實反映出各級水道的數量。

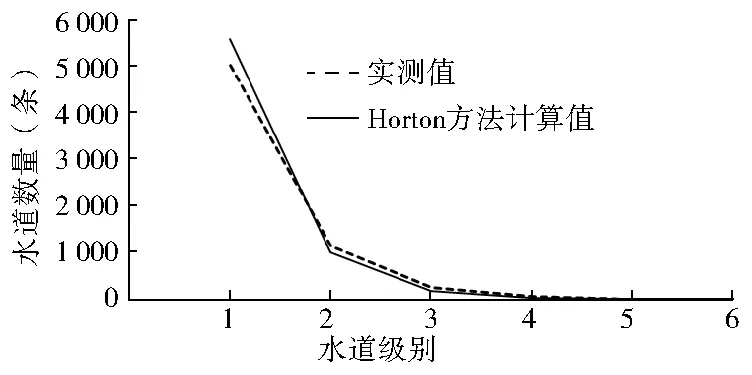
圖5 水道數量實測值與Horton方法計算值的對比

3.6 水道頻度與水道密度

水道頻度和水道密度是反映流域地貌水道發育程度的重要指標，它體現了地形破碎程度，與土壤侵蝕過程息息相關。大量研究表明，發育的水道密度在2～3 km/km2的，這種低密度的地形叫做粗結構地形，往往發生在堅硬的巖區，且地表的滲透能力強；水道密度在8～10 km/km2的，這種中密度地形往往發育在薄層砂巖和厚層頁巖地區，巖性較軟，但有大量落葉林覆蓋；水道密度在20～25 km/km2的，這種高密度或細密度結構地形往往發生在植被稀疏、巖性軟弱的地區；水道密度在100～300 km/km2的，這種極細結構地形通常發生在劣地[5]。息烽縣的水道密度為2.75 km/km2，與當地含有大量碳酸鹽巖的巖性條件和地表滲透能力強的特征是符合的，同時說明息烽縣的地形比較破碎。

4 結論與討論

(1)貴州省息烽縣典型喀斯特地區發育形成的水系網，從水系形狀上看，在負地形區發育了相當數量的星狀水系；從整個水系網的特征上看，發育的地表水系中低級水系繁多且較短，有大量低級水系向下發展匯入地下水系，其中一至四級均有部分水道匯入地下，形成地下水系。

(2)本研究得出的水道數量、水道長度、水道平均長度與水道級別的擬合關系，均與Horton定律提出的線性關系相吻合。水道分支比、長度比、水道頻度、水道密度的數值，也符合前人的研究推論。

(3)目前學術界對水系的研究方法存在一些爭議，造成這種情況的原因在于從等高線上提取水系的標準并不明確，即等高線的彎曲度為多少和由幾條等高線匯流能產生水道，缺乏相應標準。人們對水道的不同理解，導致研究結果之間出現差異，這種差異往往更多地表現在低級水道上。

(4)鑒于喀斯特地區獨特的水文地貌系統和水土流失特點，在喀斯特地區進行土壤侵蝕研究及水土保持工作時，應以流域為單元，以地表水和地下水為主線，在考慮地表水土流失的同時還要對低級水道向地下匯流所引起的地下水土流失引起足夠的重視。

[1] 梁虹，楊明德.喀斯特流域水文地貌系統及其識別方法初探[J].中國巖溶，1994，13(1)：1-8.

[2] Chorley R J, Morgan M A.Comparision of morphometric features,Unaka Mountains,Tennessee and North Carolina and Darmoor[J].Geological Society of America Bulletin,1962,73(1):17-34.

[3] Horton R E. Erosional development of streams and their drainage basins: hydrophysical approach to quantitative morphology[J]. Geological Society of America Bulletin,1945,56(2):275-370.

[4] 周家維，胡蕖.北盤江流域水系結構特征及分析[J].貴州林業科技，1997，25(1)：26-31.

[5] 承繼成,江美球.流域地貌數學模型[M].北京:科學出版社,1986:10-42.

(責任編輯 李楊楊)

“貴州省喀斯特生態與環境專業學位研究生工作站”項目(貴州省教育廳，2014)

P331

A

1000-0941(2015)05-0043-04

李圓玥(1990—)，女，貴州畢節市人，碩士研究生，主要研究方向為區域土壤侵蝕與評價；通信作者高華端(1965—)，男，貴州織金縣人，教授，博士，碩士生導師，主要研究方向為區域水土保持與環境。

2015-02-01