二階變系數線性微分方程的解

文/昌浩田 霍隆興

二階變系數線性微分方程的解

文/昌浩田 霍隆興

本文給出了一類二階線性微分方程的解法，并舉例說明。

變系數；微分方程；通解

1、預備知識

考慮二階非齊次線性微分方程[1-4]

y”+p(x)y'+q(x)y=f(x)

(1)

(其中p(x)，q(x)，f(x)是關于x的未知函數)的解；若f(x)=0，則該方程為齊次微分方程

y”+p(x)y'+q(x)y=0。

(2)

特解：若y0滿足方程y”+p(x)y'+q(x)y=0，則稱y0是該方程的一個特解。

通解：對于方程y”+p(x)y'+q(x)y=0，若y1(x)，y2(x)是該方程的兩個線性無關的解，則稱y=c1y1+c2y2(這里c1，c2為任意常數)為該方程的通解。

若知道(2)的通解為

y=c1y1(x)+c2y2(x)(這里c1，c2為常數)

通過常數變易法，設方程(1)的通解為

y=c1(x)y1(x)+c2(x)y2(x)(其中c1，c2是待定的未知函數)

由變系數二元線性方程組

解出c1'(x)，c2'(x)，再對其積分，即可求出c1(x)，c2(x)，從而可以求出方程(1)的通解。這里在知道方程(2)的一個非零特解的情況下，直接用常數變易法求方程(1)的通解。

2.主要定理及結論

若知道方程(2)的一個非零特解，則可以通過換元法化二階方程為一階方程，進而求出原方程的通解。

定理 若y1是方程(2)的一個非零解，則方程(1)的通解為

這里c1，c2為任意常數。

證明因為函數y1是方程(2)的特解，則

y1”+p(x)y1'+q(x)y1=0

(3)

由線性微分方程的性質知，函數cy1一定是方程(2)的解(c為任意的常數)。

設y=c(x)y1是方程(1)的解(其中c(x)是待定的未知函數)，將其求一、二階導數并代入方程(1)，整理得:

y1c”(x)+(2y1'+p(x)y1)c'(x)+[y1”+p(x)y1'+q(x)y1]c(x)=f(x)

由式(3)，可得

這是以c(x)為未知函數的可降階的二階線性微分方程，解之得

則：

所以方程(1)的通解為：

例:求方程(x-1)y”-xy'+y=x(x-1)2e2x的通解。

(x-1)y”-xy'+y=0

(4)

有特解y1=ex,則設該方程的通解為y=zex，代入方程(4)，化簡有

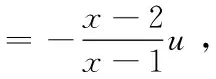
解得

積分有

故該方程的通解為

[1]羅亞平,陳仲.微分方程[M].南京:南京大學出版社,1987

[2]張學元.變系數二階線性微分方程的一個新的可解類型[J].大學數學,2003(1):96-98.

[3]東北師范大學數學系微分方程教研室.常微分方程[M].北京:高等教育出版社,1982

[4]丁同仁，李承治.常微分方程教程[M].北京：高等教育出版社，2001：18-248.

O

A

2095-9214(2015)03-0112-01

云南大學數學系)