拓撲模型下的導航地圖道路曲率引入

張 攀，鄭 珂，王軍德，朱敦堯，

拓撲模型下的導航地圖道路曲率引入

張 攀1，鄭 珂2，王軍德2，朱敦堯1，2

( 1．武漢大學衛星導航定位技術研究中心，湖北武漢430079; 2．武漢理工大學智能交通系統研究中心，湖北武漢430063)

一、引言

近年來，道路曲率在汽車導航中的作用逐漸被認識。它在先進駕駛輔助系統( ADAS)中具有廣闊的應用前景，如彎道速度提醒、輔助駕駛等［1-2］。彎道速度提醒就是根據彎道的曲率計算出最大行駛速度，提醒駕駛人注意控制車速。然而，目前的導航地圖很少包含道路曲率數據，一個重要的原因就是導航數據模型是基于拓撲關系的［3-4］，難以直接引入曲率。如導航地圖物理格式Kiwi［5］，道路模型如圖1所示。Road A對應一條多線( Multilink)，以點( node)和線( link)為基本存儲單元按出現順序存儲。線是兩個點的連線段，每個點和線都存儲自身的屬性值，如點的坐標、線的長度等。這種“直線段”的描述方式可以滿足拓撲關系的要求，便于存儲和處理，但是不能直接描述道路的曲率特性。因此，國內外研究人員提出了一些道路曲率計算方法與道路曲線描述方法［6-7］，有的甚至在存儲上取得了很好的表現［8］。但現有的導航地圖數據量大、格式固定，改變道路模型將導致工作量大、穩定性差及導航引擎不支持等問題。因此，如何在不改變道路模型的基礎上引入道路曲率數據，是道路曲率走向實際應用的關鍵。本文的基本思路是:首先在現有導航地圖道路數據的基礎上計算道路曲率，表現出道路曲率的存在形式;然后探索在拓撲模型下的道路曲率引入方法。

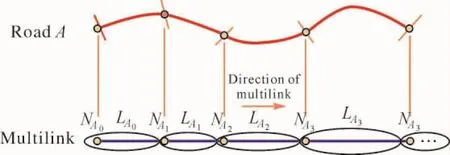
圖1 基于拓撲的道路模型

二、道路曲率計算

1．完全曲線擬合

導航地圖道路數據中含有節點的坐標數據的完全曲線擬合方法是對道路的離散節點進行曲線擬合。完全曲線擬合采用最小二乘原則，保證擬合誤差的平方和最小，得到擬合曲線方程及誤差平方和如下

式中，y*為坐標值。

然后求取擬合曲線的曲率。曲率衡量了物體的彎曲程度，是角度微分和弧長微分比值的極限

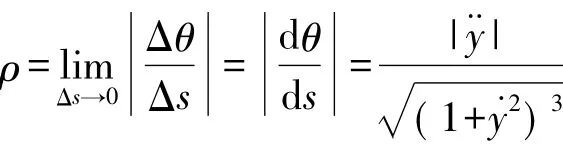
因此，保證擬合曲線二階可導時，理論上可以計算出擬合曲線上所有點的曲率。在實際應用中為了減少計算量，采取一定的簡化。如使用三次B樣體曲線擬合道路［9-10］，設當前點坐標為( xi，yi)，上一點坐標為( xi－1，yi－1)，下一個點坐標為( xi+1，yi+1)，則當前點的曲率ρi的計算方法為

2．組合線形擬合

道路的線路設計主要使用直線、圓曲線、緩和曲線3種線型。一般采用回旋曲線作為緩和曲線，以適應汽車轉彎時的行車軌跡，消除曲率突變，增進線性美觀及行車舒適感、安全感［11］。組合線型擬合就是使用道路的真實設計線型，即直線、圓曲線和回旋曲線來擬合道路。與完全曲線擬合相比，使用3種固定化的線型擬合，更加接近于道路的真實曲線性質，而且曲率計算更加容易。

首先識別線形，可以理解為將道路按直線、回旋曲線和圓曲線進行分解。簡單的方法是根據道路的曲率特征判斷，利用方位角的變化判斷線型。線路上方位角的變化是曲率沿線路的積分，較曲率而言更容易操作。基本思路是:當方位角的連續變化都接近于0時，識別為直線;當方位角在同一側保持常值變化時，識別為圓曲線;當方位角在同一側逐漸遞增或遞減時，識別為回旋曲線。

然后計算曲率。直線的曲率ρ= 0，圓曲線的曲率ρ=1/R( R為圓半徑)。如圖2所示，以回旋曲線起點為原點，起點處的切線為X軸，回旋曲線上任意一點P的曲率半徑r與該點至曲線起點的曲線長l之積為一常數，即

rl=Q2

圖2 回旋曲線

式中，Q為回旋曲線參數，是表征曲率變化緩急程度的量［12］。根據上式，回旋曲線上任一點的曲率與曲線長成比例，即回旋曲線上距起點l處的曲率為

當曲線長等于L時，曲率達到最大值，即

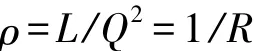
則

再取P點切線方向角為β角，有

l2=2Q2β

因此

綜上，組合線型擬合的道路曲率與道路長的函數圖像如圖3所示，理論上可以計算出任意點的曲率，同時可以使用常數描述直線和圓曲線部分的曲率。線型參數和曲率具體的計算和討論，可以參考文獻［13］，在此不作詳述。

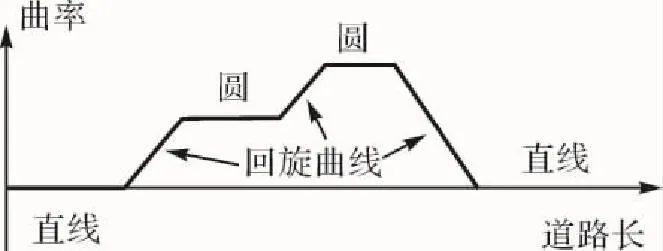
圖3 組合線形的曲率特性

三、曲率引入模型

車載導航地圖中，對道路數據的邏輯描述常采用3個層次，即數據層、描述層和綜合層［14-15］。數據層描述基本圖形要素，如點、線、面等;描述層一般用于道路引導和圖形顯示;綜合層存儲數據的拓撲結構，主要用于道路計算。曲率作為一種幾何特征，可以被引入數據層，不涉及描述層和綜合層，使其對導航地圖數據模型的影響降到最低。曲率引入數據層，具體而言就是將曲率作為一種幾何屬性引入點、線和多線，如圖4所示。

圖4 曲率引入模型

同時，道路曲率的存在形式決定著曲率的引入方式。如通過完全曲線擬合計算曲率，理論上可以計算出擬合曲線上每個點的曲率，但是不能直接表達線的曲率，不便于連續存儲和變化趨勢分析。組合線形模型可以計算每個點的曲率，同時可以直接表達線的曲率。表1對每種引入方式及其適宜的曲率計算方法進行了介紹，并分析了其優缺點。

表1 曲率引入模型

1．引入點

使用完全曲線擬合計算出的曲率非常適合引入點。直接將點的坐標帶入擬合曲線的曲率公式，計算出對應的曲率，然后將曲率作為點的屬性即可。需要使用曲率時，直接從點的屬性獲取曲率。對于使用組合線型計算出的曲率形式(見表2)，點在直線和圓曲線上的曲率值為常值，點在緩和曲線上時帶入點坐標求出該點的曲率。

表2 組合線形曲率引入點

2．引入線

使用完全曲線擬合計算出的曲率不適合引入線。使用組合線型擬合，對于直線和圓曲線部分，直接使用常值描述;對于緩和曲線，可以使用平均曲率或曲率變化區間描述，見表3。

表3 組合線形曲率引入線

3．引入多線

曲率引入多線有兩種方式:①多線曲率特征值引入。對于已經生成的多線，不必體現每個點或線的曲率，而是選取多線上的曲率特征值作為屬性，見表4。如根據某條路的曲率最大值推算最大行駛車速，根據道路上的曲率極值反演道路彎曲情況等，此時，使用完全曲線擬合與組合線型擬合都可以實現依附于多線的曲率引入。②顧及曲率分布的多線生成。多線的生成首先按照道路群分組，道路群是相關道路種別合并后的大類，如國際高速、國內高速等屬于高速;然后在每個道路群里面按照道路種別排序，根據拓撲關系和一定的規則探索生成多線，一般要求線的屬性相同，包括道路名稱、線的種類、通行方向、分離帶、道路幅員、地域信息等。顧及曲率分布生成多線，就是在探索生成多線時，顧及曲率的一致性，最理想的情況是直線部分、回旋曲線部分和圓曲線部分，各單獨生成一個多線。

表4 多線曲率特征值引入

四、試驗與結果

1．試驗數據

試驗數據采用基于經緯度和基于正規化坐標的兩種導航地圖道路數據，在Matlab中顯示，如圖5、圖6所示。正規化坐標是導航地圖物理格式使用的坐標體系，由一定范圍經緯度轉換來的區域內相對坐標，如Kiwi格式中Level1的經緯度范圍1/32(°)×1/ 32(°)對應到2047×2047的格網區域。

圖5 基于經緯度坐標的道路A

圖6 基于正規化坐標的道路B

2．曲率計算試驗

使用完全曲線擬合與組合線形擬合兩種方法，計算出試驗數據的道路曲率，結果如圖7所示。由于經緯度單位量表示的地理范圍很大，道路節點的經緯度相差很小，因此在計算曲率時，經緯度各乘以105再代入計算。將兩組完全擬合與組合線形擬合得到的曲率進行對比，表明組合線形具有較高精確度，可以滿足實際需求。

3．曲率引入試驗

將引入曲率的道路數據輸出可視化工具，發現具有較好的適應性。在不影響拓撲模型使用的同時，可以非常容易獲取點、線或多線的曲率屬性，如圖8所示。

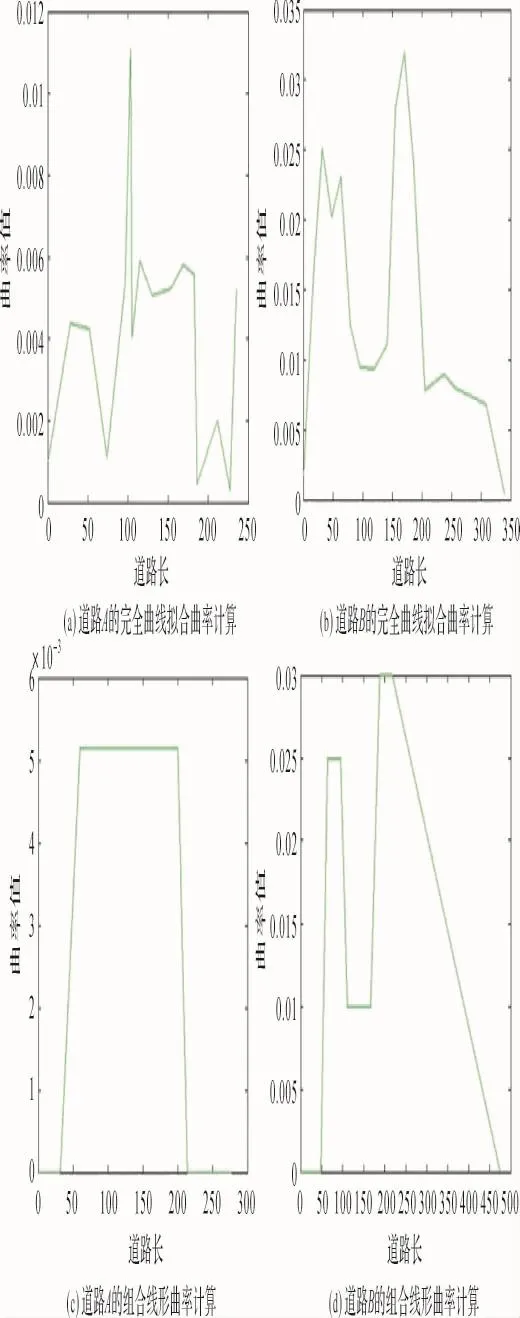
圖7 曲率計算試驗

圖8 曲率引入試驗

五、結束語

曲率作為道路的一個真實屬性，在傳統導航地圖中沒有得以表達。隨著車載導航在汽車主動安全和輔助駕駛方向的發展，道路曲率的重要性被逐漸認識。如何合理引入到現有導航地圖的數據模型，是曲率應用的瓶頸問題。本文首先研究了利用導航地圖的道路數據計算曲率，提出了完全曲線擬合與組合線形擬合兩種方法。然后根據不同的曲率存在方式，探討了道路曲率的引入方法，分別是引入點、線和多線。引入多線的兩種方法中，顧及曲率的多線生成研究尚不完善，其對導航數據的影響程度還需要進一步試驗。通過Matlab編程驗證了曲率計算兩種方法的有效性和精確性，通過可視化試驗驗證了拓撲模型下道路曲率引入的可行性。今后還需要通過車載導航系統的實車使用，驗證引入了曲率數據的導航地圖的實用性和穩定性。

［1］ LU M，WEVERS K，HEUDEN R．Technical Feasibility of Advanced Driver Assistance Systems ( ADAS) for Road Traffic Safety［J］．Transportation Planning and Technology，2005，28( 3) : 167-187．

［2］ RESS C，ETEMAD A，HOCHKIRCHEN T，et al．Electronic Horizon-supporting ADAS Applications with Predictive Map Data［C］∥ITS European Congress．Hannover:［s．n．］，2005: 18．

［3］ 張東，錢德沛，王家耀，等．嵌入式環境下導航地圖數據表示和并行調度顯示算法［J］．武漢大學學報:信息科學版，2007，32( 4) : 343-346．

［4］ 宋鶯，李清泉．實時交通信息與移動導航電子地圖融合表達［J］．武漢大學學報:信息科學版，2010，35 ( 9) : 1108-1111．

［5］ 徐敬海，李清泉，宋鶯，等．基于Kiwi數據格式的地圖顯示研究［J］．武漢大學學報:信息科學版，2005，30 ( 10) : 866-869．

［6］ 賈立山，羅劍，李世其．基于車道線直線模型的道路曲率估計方法［J］．江蘇大學學報:自然科學版，2012，33( 4) : 373-378．

［7］ JIMNEZ F，APARICIO F，ESTRADA G．Measurement Uncertainty Determination and Curve-fitting Algorithms for Development of Accurate Digital Maps for Advanced Driver Assistance Systems［J］．Transportation Research Part C: Emerging Technologies，2009，17( 3) : 225-239．

［8］ BTAILLE D，TOLEDO-MOREO R．Creating Enhanced Maps for Lane-level Vehicle Navigation［J］．IEEE Transactions on Intelligent Transportation Systems，2010，11( 4) : 786-798．

［9］ 李星軍，楊海忠．基于曲率分析的地圖匹配算法研究［J］．科學技術與工程，2012，25( 29) : 7664-7668．

［10］王獻鋒．基于曲率分析地圖匹配的車載組合導航研究［J］．科學技術與工程，2012，12( 33) : 8947-8950．

［11］葉松林．道路卵形回旋線任意點坐標及方位角計算方法［J］．測繪通報，1999( 3) : 26-28．

［12］徐海貴，王春香，楊明，等．基于曲率平滑的智能車輛道路跟蹤控制［J］．上海交通大學學報，2008，42 ( 12) : 1958-1961．

［13］姚連璧．車載GPS道路數據采集與線形參數的計算［J］．測繪學報，2002，31( S1) : 45-49．

［14］ 劉春，姚連璧．車載導航電子地圖中道路數據的空間邏輯描述［J］．同濟大學學報:自然科學版，2002，30 ( 3) : 346-351．

［15］胥銳．車載導航電子地圖的路網模型［J］．電腦知識與技術，2008，3( 7) : 1558-1559．

Introducing Road Curvature into Navigation Map Based on Topological Model

ZHANG Pan，ZHENG Ke，WANG Junde，ZHU Dunyao

隨著道路曲率的作用逐漸被認識，道路曲率引入導航地圖，成為實現先進駕駛輔助系統( ADAS)的重要途徑，也是未來導航地圖的發展趨勢之一。曲率依附于曲線存在，難以直接引入基于拓撲模型的導航地圖。為了避免模型轉換帶來的巨大工作量和不確定性，本文嘗試了拓撲模型下道路曲率引入的研究。首先在現有導航地圖道路數據基礎上，使用了完全曲線擬合與組合線型擬合兩種方法計算曲率;然后結合兩種計算方法對應的曲率存在形式，探索了在拓撲模型下的道路曲率引入方式，分別是引入點、引入線和引入多線;最后使用導航地圖道路數據進行曲率計算和曲率引入的試驗。結果表明，本文的方法具有可行性，為今后大數據量的導航地圖道路曲率引入打下了鋪墊。

拓撲模型;導航地圖;道路曲率;引入

張 攀( 1989—)，男，碩士，研究方向為車載導航電子地圖。E-mail: zhangpan@ whu．edu．cn

P282

B

0494-0911( 2015) 11-0052-05

張攀，鄭珂，王軍德，等．拓撲模型下的導航地圖道路曲率引入［J］．測繪通報，2015( 11) : 52-56．

10．13474/j．cnki．11-2246．2015．0345

2014-10-15