Investigation on nonlinear rolling dynamics of amphibious vehicle under wind and wave load

MA Xin-mou， CHANG Lie-zhen

(1. College of Mechatronic Engineering, North University of China, Taiyuan 030051， China;2. School of Science, North University of China, Taiyuan 030051， China)

馬新謀1， 常列珍2

(1. 中北大學 機電工程學院, 山西 太原 030051; 2. 中北大學 理學院, 山西 太原 030051)

?

Investigation on nonlinear rolling dynamics of amphibious vehicle under wind and wave load

MA Xin-mou1， CHANG Lie-zhen2

(1.CollegeofMechatronicEngineering,NorthUniversityofChina,Taiyuan030051，China;2.SchoolofScience,NorthUniversityofChina,Taiyuan030051，China)

Nonlinear amphibious vehicle rolling under regular waves and wind load is analyzed by a single degree of freedom system. Considering nonlinear damping and restoring moments, a nonlinear rolling dynamical equation of amphibious vehicle is established. The Hamiltonian function of the nonlinear rolling dynamical equation of amphibious vehicle indicate when subjected to joint action of periodic wave excitation and crosswind, the nonlinear rolling system degenerates into being asymmetric. The threshold value of excited moment of wave and wind is analyzed by the Melnikov method. Finally, the nonlinear rolling motion response and phase portrait were simulated by four order Runge-Kutta method at different excited moment parameters.

amphibious vehicle; nonlinear rolling motion; Melnikov method; nonlinear dynamics; crosswind load

Amphibious vehicles such as amphibious assault vehicles and amphibious armored personnel carriers have been utilized in military services for many years. Their mission specifications include amphibious operations described as to be deployed from a ship in calm to moderate seas and to reach the shore at a reasonable time. In the open literature, there are only a few published papers on the design principles and hydrodynamics of amphibious vehicles[1-2]. The amphibious vehicle’s nonlinear rolling motion is similar to that of ship in waves, so we can use the research method of ship rolling dynamics for reference to study the amphibious vehicle’s nonlinear rolling motion[3]. For a ship, the traditional stability criteria are based only on hydrostatics, and the GZ curve is used to examine if they meet the requirements based on empirical criteria. During the last three decades, a great deal of work has been done using GZ curve to predict ship capsize in wind and waves[4-8]. Melnikov’s method is one of powerful analytical methods for ship nonlinear dynamics. Falzarano, et al. applied Melnikov’s method to the single-degree-of-freedom equation of rolling motion using a cubic polynomial for the GZ curve with a nonlinear damping term for both heteroclinic and homoclinic cases[9-10].

In this paper, we will foucs on the amphibious vehicle’s nonlinear roll dynamics, with the GZ curve for determination of the restoring moment terms, the free roll decay curve for the damping moment terms, and then the Melnikov’s method for the rolling dynamics of the amphibious vehicle.

1 Nonlinear dynamical modeling of amphibious vehicles rolling motion

In this paper, we assume that the amphibious vehicles do not possess any forward speed and the amphibious vehicles rolling motion is uncoupled from other motions. A second order nonautonomous system is used as a model of amphibious vehicles rolling motion. The simple single-degree-of-freedom roll equation of motion from Refs.[11-14] is used here. It can be written as

(1)

For amphibious vehicles, like a ship, the wind heeling moment can be expressed as[15]

(2)

whereFwindis the wind heeling moment when the amphibious vehicle is upright, namely, the roll angleφ=0, and the magnitude of wind heeling moment is mainly affected by wind speed and wind area.

To facilitate the subsequent calculation, we implement cosφTaylor expansion atφ=0, thus we have

(3)

For regular wave load, it can be written as

(4)

whereFwaveandωare the regular wave heeling moment amplitude and frequency, respectively.

SubstitutingEq.(3) and Eq.(4), we have

(5)

For analytical convenience, dividing two sides of Eq.(5) byIxx+δIxx, we have

(6)

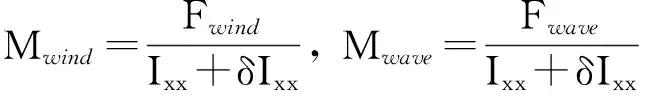
(7)

The amphibious vehicle’s general dimensions are given in Table 1[3].

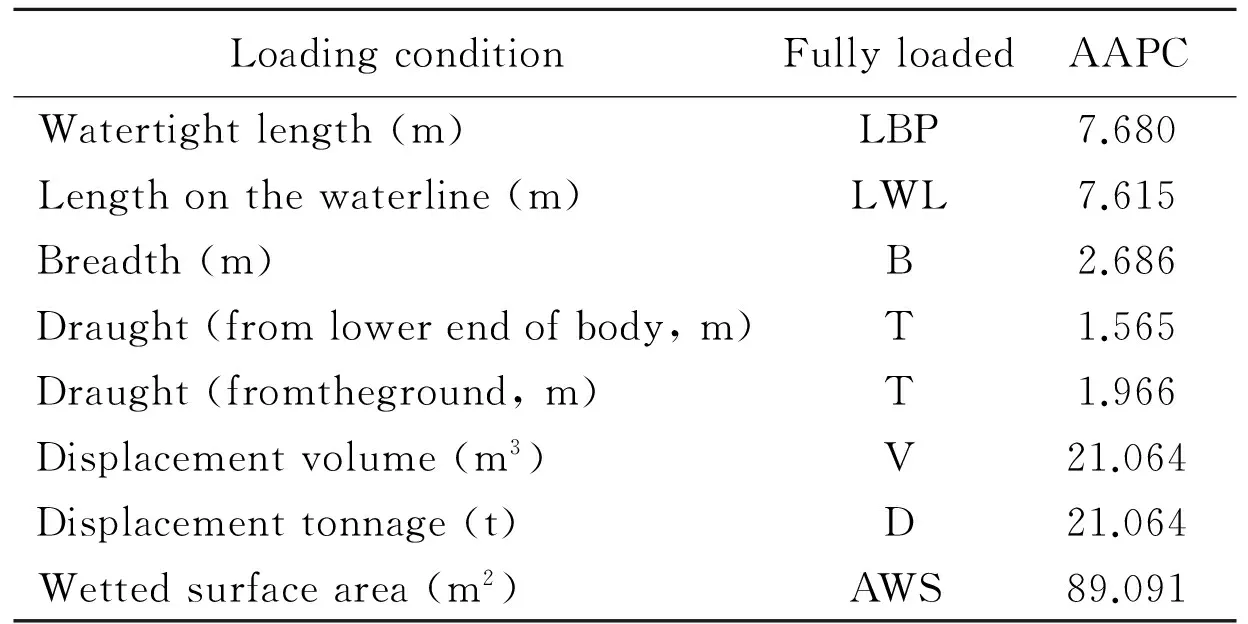
Table 1 Amphibious vehicle characteristics

In addition to floatability, the vehicle should also be stable in a floating condition. Righting arm curve of the amphibious vehicle is given in Fig.1. Although the righting arm of the amphibious vehicle is similar to the typical ship forms, we adopt the least square method to estimate the restore moment coefficientsk1andk3.

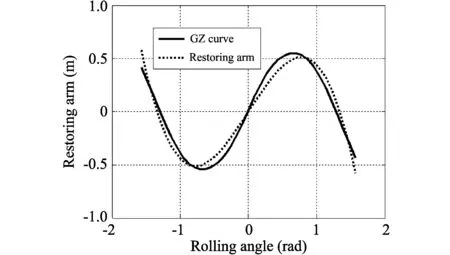
Fig.1 GZ curve of the amphibious vehicle

(8)

The distanceejfrom the data point (φj,GZj) and the fitting curve is given by

(9)

A least-squares fitting minimizes the sum of squares ofej. This minimum can be shown to result in the most probable values ofk1andk3.

We define

(10)

whereNis the number of points of GZ curve.

To minimizeWwith respect tok1andk3, we solve

(11)

Taking the partial derivatives, we have

(12)

These equations form a system of two linear equations in the two unknownsk1andk3, which is evident when rewritten it in the form

(13)

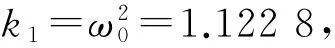
In this study, for floatability and stability analysis of the amphibious vehicle, a 1/4 scaled physical model was tested at Dalian University of Technology’s Ship Model Towing Experiment Tank (July, 2010). The obtained free rolling decay curve is shown in Fig.2[13-14].

Least square method is adopted to identify the damping coefficientsd1andd3. Let Eq.(6) right side equal to zero, we can get the free rolling motion equation of amphibious vehicle

(14)

wherek1andk3have been determined by GZ curve,d1andd3have be determined by the free rolling motion decay curve.

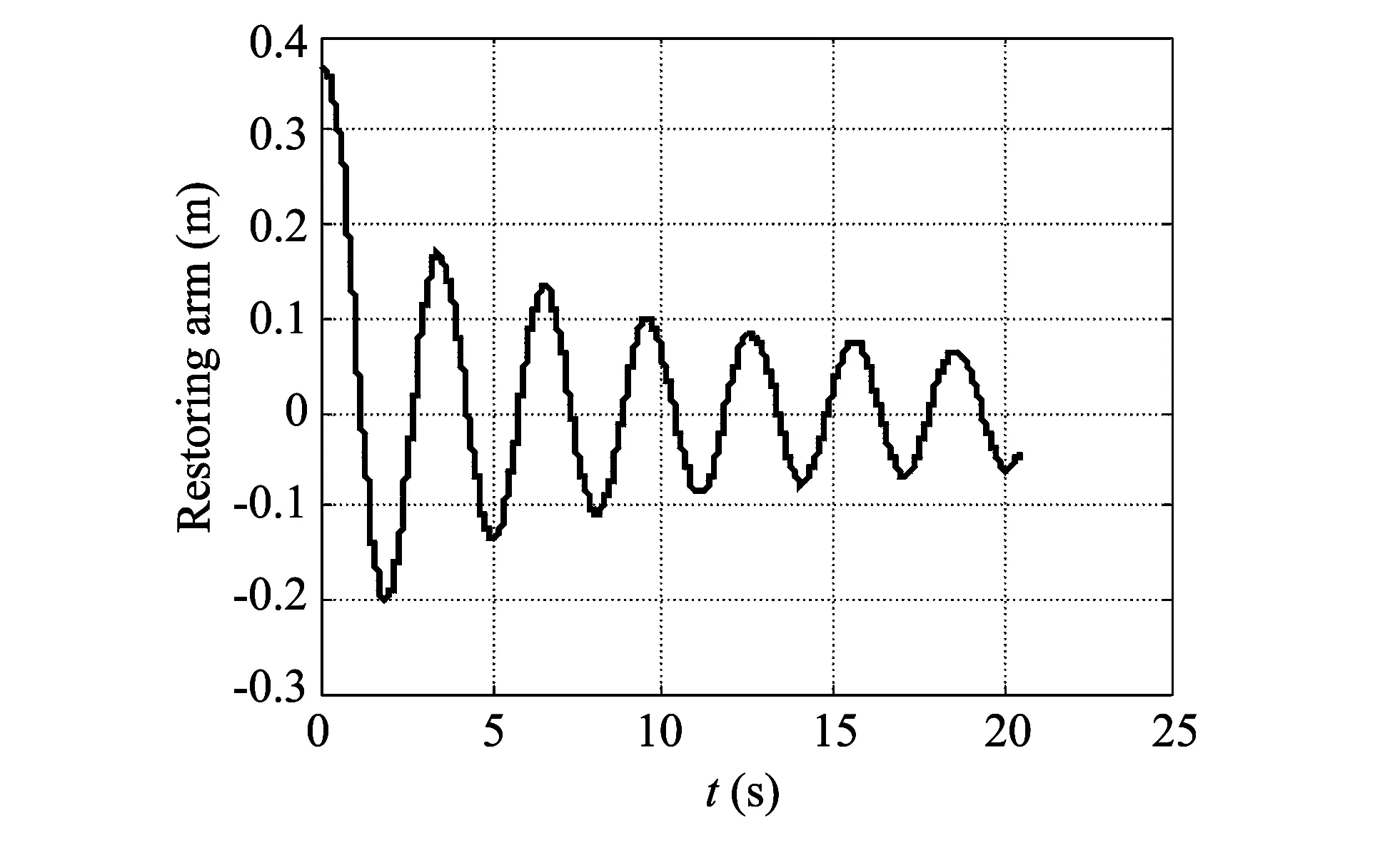
Fig.2 Free rolling decay curve of amphibious vehicle in still water

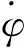
(15)

(16)

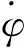
(17)

To minimizeχ2with respect tod1andd3, we solve

0.044 3 andd3=2.591 8.

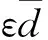
(19)

Wind load is inevitable in ship’s navigation. It is similar to amphibious vehicle rolling motion under wind and wave load. When subjected to crosswind, the amphibious vehicle rolling dynamical system is no more symmetric. The causes of asymmetry are, in essence, the even order terms in the wind load formula. The wind load is in fact fluctuating data corresponding to different wind velocities rather than a constant value. In this paper, the magnitude of wind loadMwindvaries from 0.1 to 300 according to some previous computed data.

Taking into account wind load, Eq.(7) degenerates into unperturbed Hamiltonian system Eq.(20) with potential function in Eq.(21).

(20)

(21)

The Hamiltonian function associated with Eq.(20)

(22)

The phase portraits of the system in Eq.(22) are shown in Fig.3. According to Fig.3, we can see that when subjected to crosswind, the amphibious vehicle rolling dynamical system is no more symmetrical. The two saddles are no more symmetric about y-axis and they are located at different energy levels. Meanwhile, center point has an increasing deviation from the origin with an augment in wind load. Furthermore, the safety boundaries transform from heteroclinic orbits to one homoclinic orbit and one heteroclinic orbit[16].

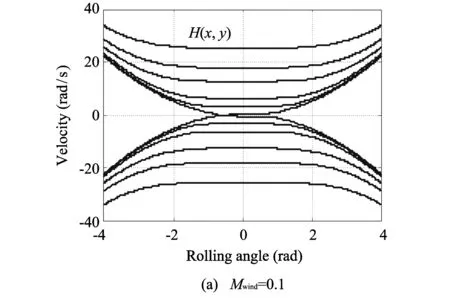
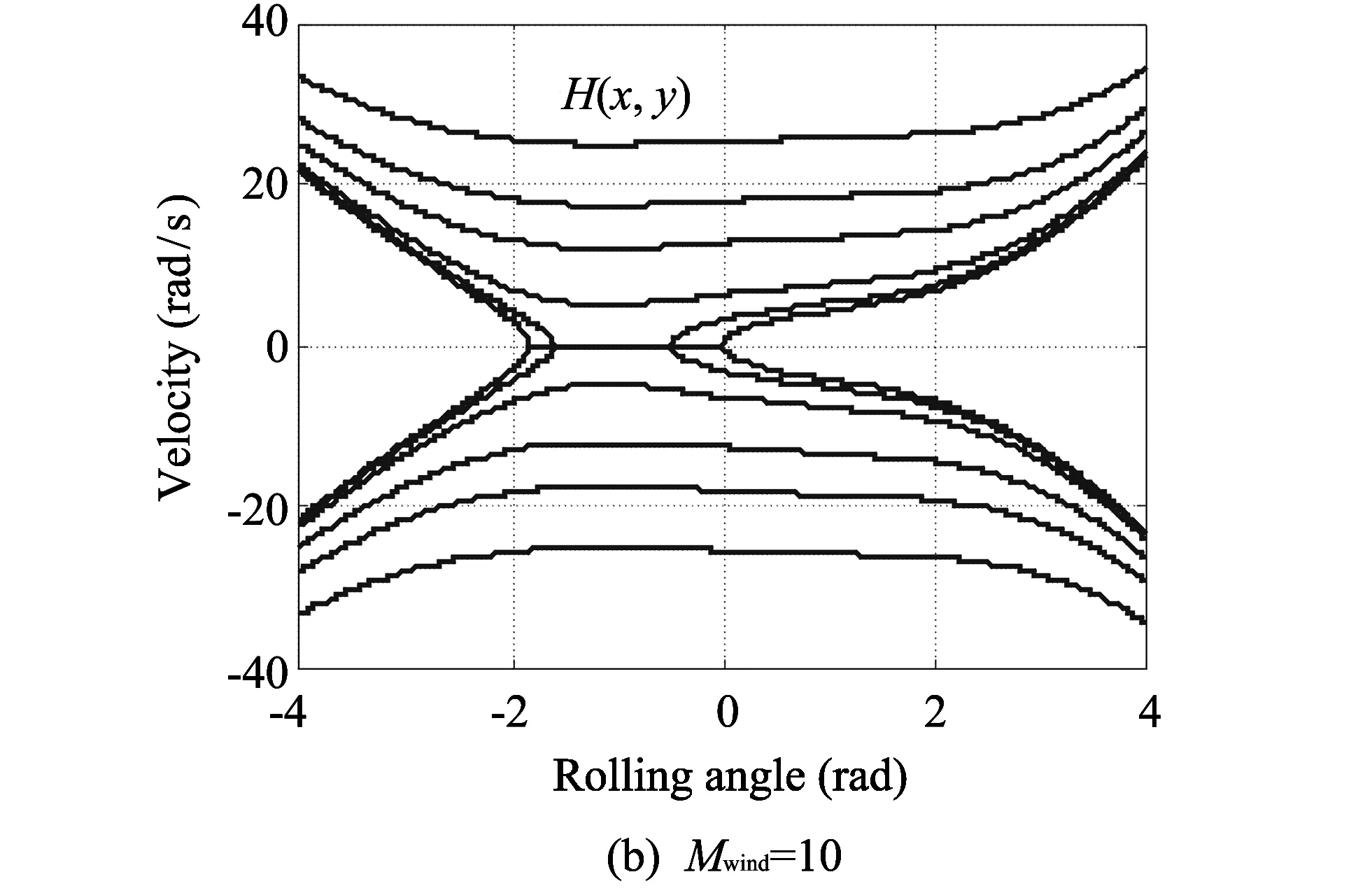
Fig.3 Phase diagram for Eq.(22)

2 Melnikov analysis

In consideration of damping and periodic perturbation of a Hamiltonian system, Melnikov function can be used to describe the way that heteroclinic orbits break up in the presence of perturbation. The Melnikov function is defined as

(23)

whereyisy(t), parametric orbit without perturbation. According to Eq.(22), we can get

(24)

From Eq.(24), we have

(25)

where (xs,ys) is the coordinate value of saddle.

Substituting Eqs.(24) and (25) into Eq.(23),

(26)

where

andxsl,xsrare thexcoordinate values of left and right saddles.

Set tanψ=I2/I1, Eq.(26) can be rewritten as

(27)

IfM(τ)>0, the threshold value can be given by

(28)

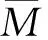
3 Numerical simulation of amphibious vehicles rolling motion

In this section, we will plot the safe basins of the amphibious vehicle rolling system and the phase portrait corresponding to four cases (different values of wind load, wave load and frequency) to analyze the motion stability and ulterior by evaluate the effect of wind load on stability. Here, We choose different values of wind loads and frequencyωto evaluate the response of the nonlinear rolling motion of amphibious vehicles rolling motion.

In Figs.4-7, the roll motion response figure shows that the roll angle displacement value decreases with the increase of time, and the nonlinear characteristic is a monotonously increasing respect to excitation frequencyω, wave loadMwaveand wind loadMwind. More portraits of nonlinear roll motion of amphibious vehicle can be calculated by Matlab routine in different load values and frequency values.

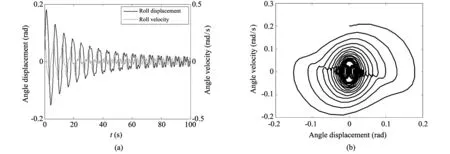
Fig.4 Nonlinear roll motion of amphibious vehicle response and phase portrait (Mwave=0.1， Mwind=0.0， )

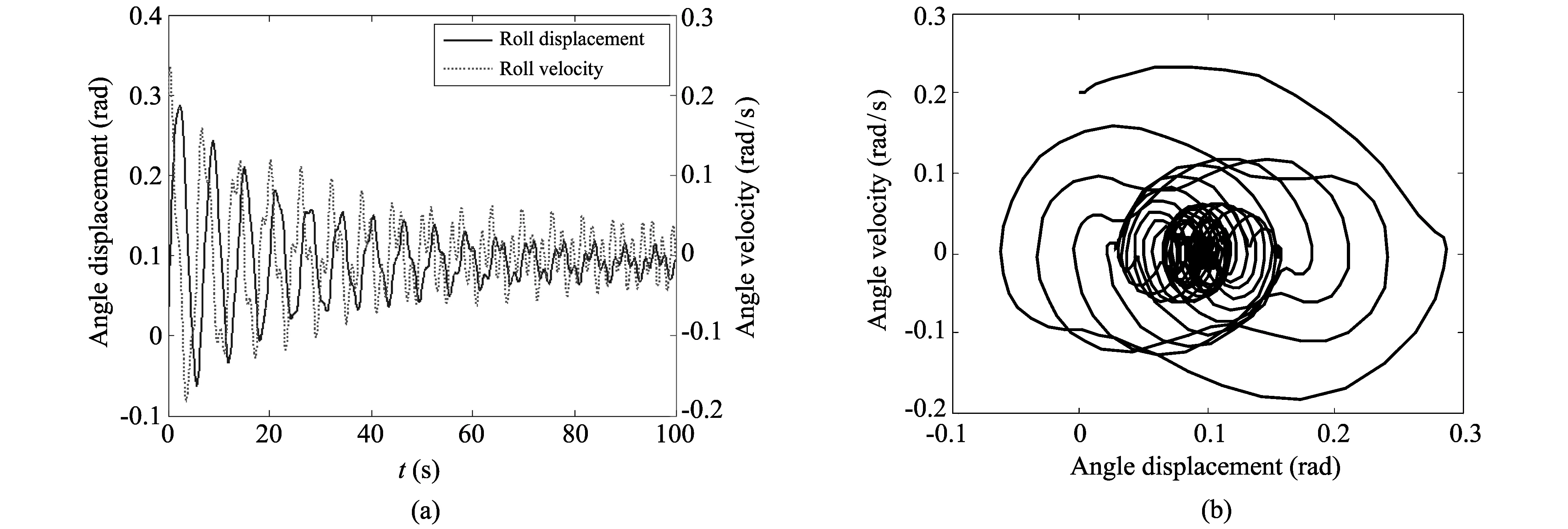
Fig.5 Nonlinear roll motion of amphibious vehicle response and phase portrait (Mwave=0.1, Mwind=0.1, )

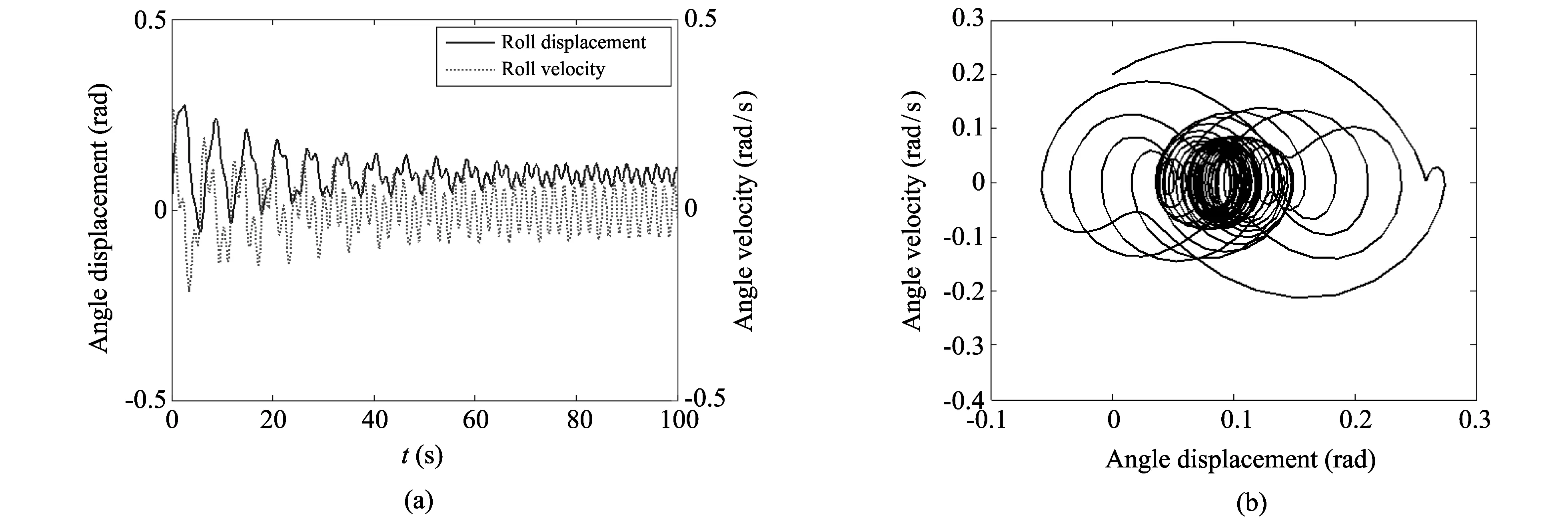
Fig.6 Nonlinear roll motion of amphibious vehicle response and phase portrait (Mwave=0.2， Mwind=0.1， )

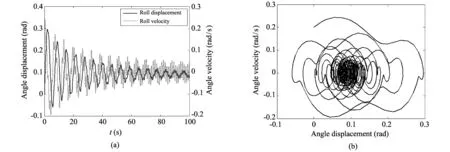
Fig.7 Nonlinear roll motion of amphibious vehicle response and phase portrait (Mwave=0.2， Mwind=0.1， )

4 Conclusion

For amphibious vehicle rolling dynamical system, the heteroclinic orbits are symmetric without wind load or other biased terms; while the symmetry begins to break when the system is subjected to cross wind. As asymmetric parameters,Mwind,Mwaveandωhave critical effects on degree of asymmetry. Numerical method can be used to solve the simple zero point of Melnikov function in nonlinear dynamical system. It expands the range of applicable systems and improves the computation efficiency of threshold value. The analysis in this paper has some significance for amphibious vehicle navigation and stability assessment.

[1] Chun H H, Ahn B H， Cha S M. Self-propulsion test and analysis of an amphibious tracked vehicle with waterjet. In: Proceedings of World Maritime Technology Conference and SNAME Annual Meeting, USA, 2003.

[2] Sticker J G, Becnel A J, Purnell J G. Advanced waterjet systems. Naval Engineers Journal, 1994, 106 (5): 100-109.

[3] Helvacioglu S, Helvacioglu I H, Tuncer B. Improving the river crossing capability of an amphibious vehicle. Ocean Engineering, 2011, 38(17/18): 2201- 2207.

[4] Spyrou K J, Cotton B, Gurd B. Analytical expressions of capsize boundary for a ship with roll bias in beam waves. Journal of Ship Research, 2002, 46(3): 125-135.

[5] Neves M A S, Rodriguez C A. On unstable ship motions resulting from strong non-linear coupling. Ocean Engingeering, 2006, 33(13/14): 1853-1883.

[6] Falzarano J M. Predicting complicated dynamics leading to vessel capsizing. Ann Arbor: University of Michigan, 1990.

[7] Falzarano J M, Shaw S W, Troesch A W. Application of global methods for analyzing dynamical systems to ship rolling motion and capsizing. International Journal of Bifurcation and Chaos, 1992, 2: 101-115.

[8] WU Wan, McCue L. Application of the extended Melnikov’s method for single-degree-of-freedom vessel roll motion. Ocean Engineering, 2008, 35(1): 1739-1746.

[9] Ueno K, Kimura N, Amagai K. Estimation of coefficients of the equation of nonlinear roll motion for fishing boats by improved energy method and genetic algorithm. Japan Journal of Industrial and Applied Mathematics, 2003, 20(2): 155-192.

[10] Jang T S, Choi H S, Han S L. A new method for detecting non-linear damping and restoring forces in non-linear oscillation systems from transient data. International Journal of Non-Linear Mechanics, 2009, 44(7): 801-808.

[11] MA Xin-mou, PAN Yu-tian, CHANG Lie-zhen, et al. Study on nonlinear rolling motion dynamics of amphibious combat weapon. Journal of Gun Launch & Control， 2010, (4): 66-69.

[12] MA Xin-mou, PAN Yu-tian, CHANG Lie-zhen, et al. Lyapunov characteristic exponents for analyzing the nonlinear rolling motion of amphibious vehicle. Journal of North University of China (Natural science edition)， 2011, 32(4): 448-453.

[13] MA Xin-mou, PAN Yu-tian, CHANG Lie-zhen. Estimated nonlinear damping coefficients of amphibious vehicle roll motion. Journal of Ship Mechanics， 2013, (5): 488-493.

[14] MA Xin-mou, CHANG Lie-zhen, HOU Hong-hua. Research on dynamics parameters identification for amphibious vehicle nonlinear rolling motion. Journal of North University of China (Natural science edition)， 2015, 36(2): 134-139.

[15] LIU Ya-chong, HU An-kang, HAN Feng-lei, et al. Stability analysis of nonlinear ship-roll dynamics under wind and wave. Chaos, Solitons & Fractals， 2015, 76: 32-39.

[16] Manucharyan G V, Mikhlin Y V. The construction of homoclinic and heteroclinic orbits in non-linear systems. Applied Mathematics and Mechanics, 2005, 69: 39-48.

風浪激勵下的兩棲車輛非線性橫搖動力學研究

采用單自由度系統研究了兩棲車輛在規則波浪和風載荷激勵下的非線性橫搖動力學， 建立了考慮非線性阻尼和非線性恢復力矩的非線性橫搖動力學方程。 非線性橫搖動力學方程對應的哈密爾頓函數表明， 當只有波浪擾動力矩作用時， 非線性橫搖運動是對稱的； 當有風載荷作用時， 兩棲車輛的非線性橫搖運動不在對稱。 采用梅爾尼科夫法給出了激勵幅值的閾值范圍。 最后， 采用四階龍格庫塔法對兩棲車輛的非線性橫搖運動方程在不同的外載荷參數下進行數值積分。 結果表明， 兩棲車輛橫搖在風浪聯合作用下表現出明顯的非線性特性。

兩棲車輛； 非線性橫搖； 梅爾尼科夫法； 非線性動力學； 側風載荷

MA Xin-mou， CHANG Lie-zhen. Investigation on nonlinear rolling dynamics of amphibious vehicle under wind and wave load. Journal of Measurement Science and Instrumentation, 2015, 6(3)： 275-281. [

馬新謀1， 常列珍2

(1. 中北大學 機電工程學院, 山西 太原 030051; 2. 中北大學 理學院, 山西 太原 030051)

10.3969/j.issn.1674-8042.2015.03.013]

Received date： 2015-05-20 Foundation items： The Pre-research Project of the General Armament Department; The Science Fund of North University of China (No.20130105)

MA Xin-mou (maxinmou03@163.com)

1674-8042(2015)03-0275-07 doi： 10.3969/j.issn.1674-8042.2015.03.013

CLD number： TJ811+.6 Document code： A