74LS160實現N進制計數器的方法和EWB仿真

威海職業學院 王小方

?

74LS160實現N進制計數器的方法和EWB仿真

威海職業學院 王小方

【摘要】本文以74LS160實現24進制加法計數器為例，介紹了反饋清零法和反饋置數法實現N進制計數器，并通過EWB仿真實驗演示實驗結果。

【關鍵詞】計數器；反饋清零；反饋置數；仿真

計數器是記憶時鐘脈沖個數的數字電路，作為一種最典型的時序邏輯電路，在各類數字系統中有著廣泛的應用。構成計數器的方法主要有兩種：（1）用觸發器加上必要的門電路實現；（2）利用集成計數器實現，這種方法從設計原理到硬件實現都相對簡單，因而較為常用。

1 74LS160的邏輯功能

74LS160是同步十進制加法計數器，如表1所示。

表1　74LS160功能表

說明：（1）異步清零，清零操作不受CP脈沖和其他輸入信號的影響。（2）同步置數，置數操作與CP脈沖上升沿同步。（3）數據保持，當CR=1，LD=1,使能端CTT，CTP邏輯與為0時，輸出端具有數據保持功能。（4）加法計數，當CR=LD=CTT=CTP=1,且CP上升沿時，輸出端加法計數。

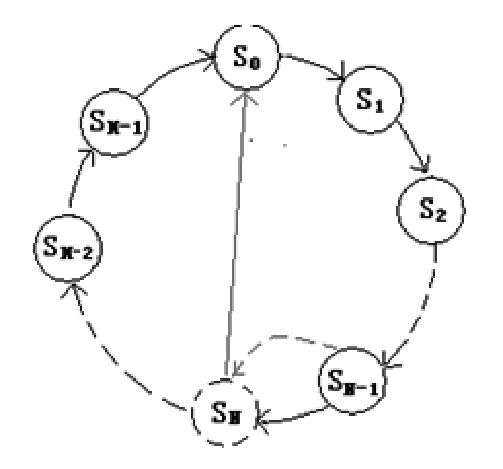
圖1　異步清零法實現N進制計數器

圖2　同步清零法實現N進制 計數器

2 反饋清零法

現有M進制集成計數器，設計N進制計數器。若M>N，若從全零初始狀態S0開始計數，第1個時鐘到來時，計數狀態為S1，第N-1時鐘到來時，計數狀態為SN-1，當所用計數器具有異步清零的功能時，則跳轉信號為SN，即第N 時鐘到來時，使計數狀態返回S0，原M進制集成計數器中的SN～SM-1這M-N個狀態被跳過。如圖1所示。當所用計數器具有同步清零的功能時，則跳轉信號是SN-1，即第N-1個時鐘到來時，使計數狀態返回S0，如圖2所示。

3 反饋置數法

同清零法，首先根據要求設定置數端的狀態Sa，第1個時鐘到來時，計數狀態為Sa+1，以此類推，第N-1時鐘到來時，計數狀態為Sa+N-1，當所用計數器具有異步置數的功能時，則跳轉信號為Sa+N，即第N時鐘到來時，使計數狀態返回Sa。當所用計數器具有同步置數的功能時，則跳轉信號是Sa+N-1，即第N-1個時鐘到來時，使計數狀態返回Sa，以74LS160實現七進制計數器為例。設定置數狀態為0010（Sa），因74LS160具有同步置數功能，因此跳轉信號為1000（Sa+N-1）。

4 EWB仿真用74LS160實現24進制計數器

EWB軟件是加拿大Interactive Image Technologies公司于八十年代末、九十年代初推出的電子電路仿真的虛擬電子工作臺軟件。它帶有豐富的電路元件庫，它提供的虛擬儀器可以用比實驗室中更靈活的方式進行電路實驗和仿真。

4.1 異步清零法實現24進制計數器

要通過74160實現24進制，需要采用2個集成塊，低位片保持十進制不變，即0000～1001，每經過10個脈沖信號，低位片的進位輸出端(RCO)就向高位片使能端（CTP、CTT）輸送計數信號“1”，高位片叢0000開始計數，最終過渡態為高位片QDQCQBQA=0010，低位片QDQCQBQA=0100，經過與非門后形成CLR’=0信號完成置零，實現一個計數周期的循環。如圖3所示。

4.2 同步置數法實現24進制計數器

同異步清零法，需要采用2個集成塊，低位片保持十進制不變，即0000～1001，每經過10個脈沖信號，低位片的進位輸出端(RCO)就向高位片使能端（CTP、CTT）輸送計數信號“1”，高位片叢0000開始計數，最終過渡態為高位片QDQCQBQA=0010，而低位片QDQCQBQA=0011，經過三輸入與非門后形成LOAD’=0 信號完成置零，實現一個計數周期的循環。如圖4所示。

圖3　清零法實現24進制計數器

圖4　置數法實現24進制計數

5 結束語

文中以集成計數器74LS160為基礎，采用清零法和置數法，實例設計24進制計數器，并應用EWB進行電子電路設計和仿真，利用豐富的元器件庫和實用的虛擬儀器，操作簡單快捷，修改方便。缺點是示波器多為雙蹤示波器無法同時觀測多路波形。

參考文獻

[1]余孟嘗.數字電子技術基礎簡明教程[M].北京:高等教育出版社,2010.

[2]任駿原.數字電子技術實驗[M].沈陽:東北大學出版社, 2010.

[3]胡立濤.EWB電子仿真實驗指導書[M].南海出版公司,2006.

[4]陳先榮.EWB在電子技術實驗中的輔助教學應用[J].實驗技術與管理,2006,23(10):88-90.

王小方（1980—）， 女， 威海職業學院講師，主要從事電子技術的教學研究。

作者簡介：