SIS中考慮功能測試的Markov建模分析

Analysis of Markov Modeling Considering Functional Test for SIS

王慧鋒　龍　飛

(華東理工大學信息科學與工程學院，上海　200237)

SIS中考慮功能測試的Markov建模分析

Analysis of Markov Modeling Considering Functional Test for SIS

王慧鋒龍飛

(華東理工大學信息科學與工程學院，上海200237)

摘要：采用Markov建模方法計算安全完整性水平(SIL)時，為了使計算結果更加精確，對安全儀表系統(SIS)中帶診斷電路的系統建模時加入考慮功能測試的條件進行重新建模。利用重建的模型計算出系統在功能測試后的測試時間間隔內的平均要求時失效概率，進而得出SIS的SIL等級，并與未考慮功能測試條件建模的計算結果進行比較。通過分析得出考慮功能測試條件建模時計算得到的結果相對精確，并以化工裝置中的加氫裝置為例進一步驗證了理論研究結果的正確性和適用性。

關鍵詞：安全儀表系統Markov模型功能測試安全完整性等級冗余結構失效率診斷電路

Abstract：For the system with diagnostic circuit in safety instrumented system (SIS), to calculate safety integrity level (SIL) by adopting Markov modeling method, in order to improve the accuracy of calculation, the functional test condition is taken into account for model reconstruction. From the rebuilt model, the PFDavg of the system in the test interval after the functional test is calculated; then come to the SIL of SIS. The calculated result is compared with that by using the method in which the functional test is not taken into account. Through analyzing, it is found that the method proposed obtained more accurate result, and with the hydrogenation unit in chemical industry as example, the correctness and applicability of the result of theoretical research are verified.

Keywords：SISMarkov modelFunctional testSILRedundant structureFailure rateDiagnostic circuit

0引言

在石化裝置中，安全儀表系統(safety instrumented system,SIS)已被廣泛應用，用來確保生產過程的安全，降低風險[1-2]。為了確保安全儀表系統能夠正確地執行其安全功能，滿足要求的安全完整性等級(safety integrity level,SIL)，SIS在投入運行前需要對其進行功能安全評估，確定其 SIL等級[3]。為了計算SIL等級， IEC 61508標準中給出了故障樹分析[4]、可靠性框圖[5]以及Markov建模[6]的定量計算方法，其中，Markov建模方法應用較好[7]。

IEC 61508標準中介紹了幾種冗余結構的Markov模型的建模方法[8]。文獻[9]在對1oo1D和2oo2D結構的系統建模時還考慮了診斷電路的失效概率，使得模型的全面性和完整性得到進一步提高，但這些模型計算出的平均要求時失效概率(average probability of failure on demand，PFDavg)只是在一個功能測試間隔內的，不能對功能測試[10]期間的失效和修復行為進行定量計算。在實際生產過程中，功能測試是很有必要的。本文在文獻[9]的基礎上，以 1oo1D和 2oo2D冗余結構的 SIS為例，對帶診斷電路的SIS重新建立Markov模型，分析功能測試(本文僅討論在線功能測試)對SIL等級確定的影響。

1Markov建模方法簡介

安全儀表系統中定量計算SIL等級的建模方法所使用的 Markov模型采用狀態轉移圖表示系統的狀態變化。系統的狀態(可以是正常、失效或者中間狀態)用圓圈來表示，系統狀態轉移用帶箭頭的一條弧線表示，起點表示轉移前系統狀態，終點表示轉移后系統狀態，弧線上方標注的數值代表各個狀態之間的轉移概率[6](通常用λ表示失效率，μ表示修復率)。Markov模型示例如圖1所示。

圖1　Markov模型示例

圖1所示模型中有兩個狀態：正常(狀態0)和失效(狀態1)，狀態0可能以失效率λ1轉移到狀態1，而狀態1可以通過修復率μ0恢復到狀態0。由 Markov模型可以得到系統的狀態方程，對此方程進行求解并根據 IEC 61508中的公式就可以計算出PFDavg。

2考慮功能測試的Markov模型

1oo1D和 2oo2D 是典型的兩個帶診斷通道的冗余結構，本文將對安全儀表系統中邏輯控制器模塊的 1oo1D和 2oo2D結構進行建模分析，表1列出了模型中用到的符號含義，表2為IEC 61508中低要求操作模式下 SIL等級劃分表。

表1　模型中的符號含義

表2　安全完整性水平劃分表

2.1　1oo1D結構的Markov模型

未考慮功能測試條件下，1oo1D結構加入診斷模塊失效率(圖中虛線部分)的Markov模型如圖2所示。

狀態轉移矩陣如下所示。

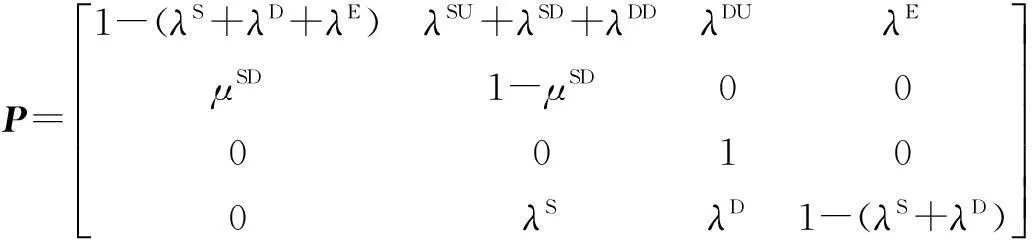
1oo1D結構的PFDavg可以由式(1)計算得到：

PFDavg=S0PTIVD

(1)

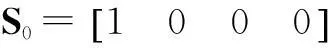
圖2　1oo1D考慮診斷模塊失效率的Markov模型

考慮功能測試條件時，未檢測到的危險失效(狀態2)就可以通過功能測試發現，并以μ1的修復率(圖中虛線部分)恢復到正常狀態。考慮功能測試的Markov模型如圖3所示，其狀態轉移矩陣如下所示。

圖3　1oo1D考慮功能測試的Markov模型

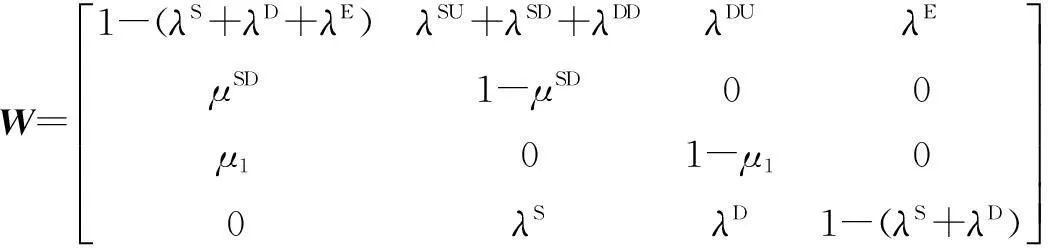
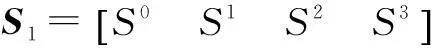
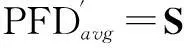
(2)

2.2　2oo2D結構的Markov模型

同樣，可以建立 2oo2D冗余結構加入診斷模塊失效率的 Markov模型，如圖4所示。其狀態轉移矩陣如式(3)所示，2oo2D的狀態相對復雜，共有9個狀態。

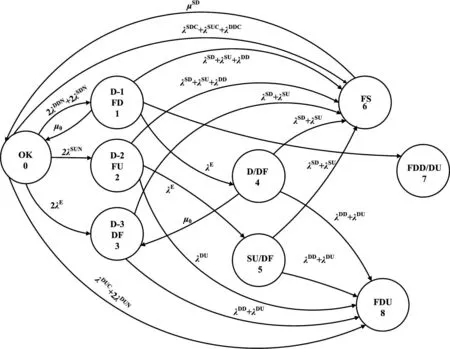
圖4　2oo2D考慮診斷模塊失效率的Markov模型

同理，考慮功能測試的Markov模型如圖5所示，其中的虛線表示未檢測到的危險失效(狀態2、5、7、8)。未檢測到的危險失效可以通過功能測試發現并修復(修復率為μ1)，狀態轉移矩陣如式(4)所示。式(3)和式(4)中Σ表示矩陣中當前行其他元素之和。

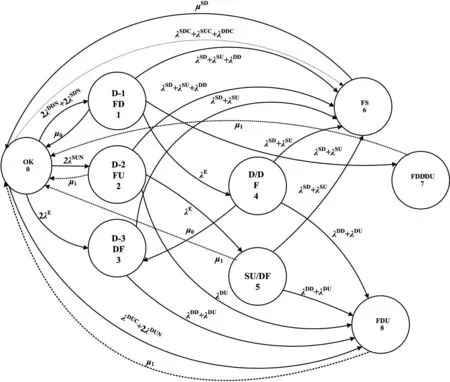
圖5　2oo2D考慮功能測試的Markov模型

(3)

(4)

3理論分析

考慮功能測試后重新建立的Markov模型在一定程度上會影響到SIL等級的計算結果，利用上述對1oo1D和2oo2D冗余結構建立的模型，以邏輯控制器為研究對象，做計算分析。計算中做以下規定。

① 設備失效率取為：λSD=1.007×10-6、λSU=9.900×10-8、λDD=5.900×10-7、λDU=1.180×10-7、λE=9.4×10-8，共因失效因子β=0.05。

② 儀表故障在線修復時間TD= 8 h,則μ0=1/8=0.125；功能測試周期為1年(8 760 h)，一次無故障停車后裝置重啟時間為 24 h，則μSD=1/24=0.042。假定功能測試是理想的，即CTI=100%。

③ 一個功能測試周期后，各狀態都達到了極限狀態概率。

3.1　1oo1D冗余結構計算結果

由式(1)可以求出未考慮功能測試時的平均要求時失效概率:

PFDavg=1.9×10-3

(5)

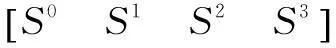
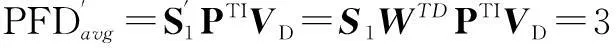
(6)

3.2　2oo2D冗余結構計算結果

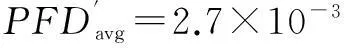
3.3　計算結果分析

與表2對比可以得出，上述兩組計算結果中，未考慮功能測試和考慮功能測試條件時計算的結果所對應的SIL等級都為SIL2，但考慮了功能測試之后得到的PFDavg稍微偏大，而未考慮功能測試時計算的結果相對保守，一定程度上會高估SIL等級，影響其精確性。

圖6　誤差e隨u1的變化曲線

從圖6可以看出,隨著測試覆蓋率的不斷增大，雖然兩者的誤差不斷減小，但始終保持在0.001 1的范圍之內。對照表2可以看出,雖然這個誤差對SIL1和SIL2等級的計算影響不大，但對SIL3和SIL4等級的系統將影響其計算結果的精確性。如果高估安全儀表系統的SIL等級，在實際工程應用中對安全儀表系統的投入成本就會相對增加，一定程度上會降低企業的經濟效益。因此，SIL等級計算的精確性在實際應用中具有重要意義。

4理論應用

以上是對 1oo1D和 2oo2D結構Markov建模方法計算SIL等級進行的理論分析，為了驗證理論分析結果在實際應用中是否具有正確性和適用性，以加氫裝置為例，做進一步探討。對于工況較為復雜的加氫裝置必須設置安全儀表系統來保證生產過程的安全[13]，加氫裝置的工藝背景和工藝流程在文獻[14]中有詳細描述，這里不一一贅述，僅以加氫裂化反應器入口溫度安全儀表功能為例，對其進行相關安全儀表的SIL等級計算。循環氫加熱爐燃氣壓力安全儀表系統框圖如圖7所示。

圖7　循環氫加熱爐燃氣壓力安全儀表系統框圖

在該安全儀表系統中，使用熱電偶對加氫裂化反應器入口處溫度進行檢測，檢測到的信號傳輸到溫度變送器，溫度變送器將標準的4~20 mA信號輸出到報警設置，邏輯控制器根據報警設置輸出的開關量信號執行相應的安全聯鎖邏輯。當檢測到反應器入口溫度過高時， 邏輯控制器會執行聯鎖動作來關閉閥門 XCVI-11和 XCVI-16，去長明燈和去主火嘴的燃料氣將會被切斷，從而熄滅長明燈和火嘴，防止由于溫度過高引起反應失控。

同樣以邏輯控制器為研究對象做進一步探討，可以看出圖7中邏輯控制器系統結構為 1oo1的冗余結構，下面通過建立Markov模型對其SIL等級進行計算。其未考慮功能測試的Markov模型如圖8所示。

圖8　1oo1結構的Markov模型

其狀態轉移矩陣如式(7)所示。

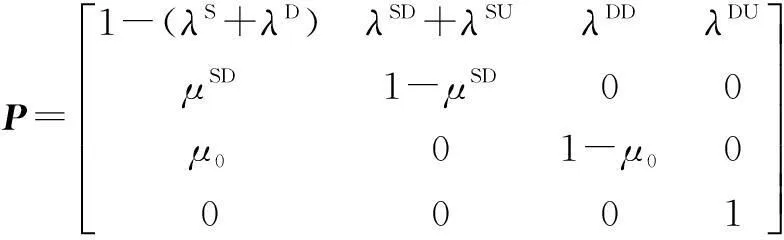
(7)

考慮功能測試的Markov模型如圖9所示。

圖9　1oo1結構考慮功能測試的Markov模型

其狀態轉移矩陣如式(8)所示。

(8)

設備的相關失效數據[15]如表3所示。對于邏輯控制器部分，采用前面同樣的方法計算，得出未考慮功能測試時PFD1=1.04×10-3;考慮功能測試時的計算結果為PFD2=1.4×10-3。從計算結果可以看出，加氫裝置的邏輯控制器模塊的SIL等級達到了SIL2。同樣，未考慮功能測試時的計算結果相對保守，而考慮了功能測試后的計算結果稍微偏大，相對精確，這和理論分析上的結果保持一致，從而證明了理論分析的正確性。另外,加氫裝置邏輯控制器部分是 1oo1的冗余結構，進一步說明了上述理論對其他系統結構同樣具有適用性。

表3　相應設備失效率

5結束語

對于1oo1D和2oo2D冗余結構的系統，分別建立未考慮功能測試和考慮功能測試的 Markov模型，并通過對 Markov模型求解，進一步計算出平均要求時失效概率，得出其SIL等級。將考慮功能測試的計算結果與未考慮功能測試時的計算結果進行比較，可以看出考慮功能測試后的計算結果相對精確，能更好地對化工裝置中的安全儀表系統進行 SIL等級評估。通過對加氫裝置的控制器部分進行 SIL等級計算，進一步驗證了本文理論分析結果的正確性和適用性。

參考文獻

[1] 張雙亮，李慶濤.海洋石油平臺安全儀表系統的設計與應用[J].自動化儀表,2011,32(9):83-86.

[2] 龔義文.安全儀表系統在化工裝置中的應用[J].自動化儀表,2010,31(12):50-54.

[3] 黃文君，何偉挺，邊俊.安全儀表系統的功能安全設計[J].自動化儀表,2010,31(7):75-78.

[4] Dutuit Y,Innal F,Rauzy A,et al.Probabilistic assessments in relationship with safety integrity levels by using Fault Trees[J].Reliability Engineering and System Safety,2008,93(12):1867-1876.

[5] Catelani M,Ciani L,Luongo V.A simplified procedure for the analysis of Safety Instrumented Systems in the process industry application[J].Microelectronics Reliability,2011,51(9-11):1503-1507.

[6] Bukowski J,Goble W.Using Markov models for safety analysis of programmable electronic systems[J].ISA Transaction,1995,34(2):193-198.

[7] Zhang T L,Long W,Sato Y.Availability of systems with self-diagnostic components-applying Markov model to IEC 61508-6[J].Reliability Engineering and System Safety,2003,80(2):133-141.

[8] International Electrotechnical Commission.IEC 61508 Functional safety of electrical/electronic/programmable safety-related system[S].2000.

[9] 王慧鋒，張亨，湯陳懷，等.SIS中基于Markov模型的診斷模塊失效率分析[J].化工自動化及儀表,2012,40(2):196-199.

[10]Torres-Echeverria A C,Martorell S,Thompson H A.Modelling and optimization of proof testing policies for safety instrumented systems[J].Reliability Engineering and System Safety,2009,94(4):838-854.

[11]陽憲惠，郭海濤.安全儀表系統的功能安全[M].北京：清華大學出版社,2007：90-91.

[12]陳偉，趙建平.功能測試條件下安全儀表系統失效概率預測方法[J].石油化工設備,2012,41(1):80-82.

[13]宋小寧.加氫裝置安全儀表系統設計[J].自動化儀表,2008,29(11):64-68.

中圖分類號：TH701

文獻標志碼：A

DOI:10.16086/j.cnki.issn1000-0380.201502015

修改稿收到日期：2014-08-09。

第一作者王慧鋒(1969-),女，1992年畢業于華東理工大學生產過程自動化專業，獲博士學位，教授；主要從事檢測技術及自動化裝置的研究。